无线电引信回波信号的滤波算法

王 晓，赵河明，彭志凌

(中北大学机电工程学院，山西 太原 030051 )

0 引言

无线电引信又称雷达引信，是利用无线电波觉察目标以获取引爆信息确定引爆时机。现代战争要求引信能从繁杂的信号中获取准确的目标信息。无线电引信易受干扰信号的影响[1]。使得引信回波信号的滤波问题成为无线电引信的一个重要研究方向。

引信回波信号的最高频率为吉赫兹，被噪音覆盖，很难得到实际波形。引信回波的处理方法有小波分析和自适应滤波等方法。其中自适应滤波算法有计算简便、稳定性好和易实现等优点，广泛应用于实际工程。

自适应滤波技术[2-4]作为当前主流的噪声消除模块[5]，其理论模型最早于1960年由Widrow和Hoff 提出。它作为信号处理方向的具体应用分支，能够根据系统环境和噪声特点自适应地改进滤波器的滤波参数，使得滤波器能够动态地调整输入信号，提取有用信号，达到最佳滤波的效果[4]。收敛速度和稳态误差是自适应滤波算法的两个重要技术指标。在高收敛速度和低稳态误差情形下才能有效过滤回波信号中的杂波。文献[6-8]建立了步长与误差的非线性关系模型，提高了收敛速度降低了稳态误差，但其只考虑了当前误差对步长的影响。文献[9-10]弥补了文献[6-8]的缺陷，但其在提高收敛速度降低稳态误差方面仍有待提高。文献[11-12]建立了步长与误差的非线性关系模型，但对高频信号的消除不够有效。文献[13]中利用了反馈理论知识，建立了当前步长跟当前误差比率的平方相关的步长与误差的非线性关系模型，并应用于引信回波信号的滤波，但其误差抑制能力还有待提高。对此，本文提出无线电引信回波信号的变步长LMS自适应滤波算法。

1 自适应滤波算法

1.1 自适应滤波算法原理

自适应滤波器基本原理如图1所示。图1中，x(n)为输入信号，y(n)为输出信号，v(n)为与x(n)不相关的杂波信号，d(n)为期望信号，误差e(n)=d(n)-y(n)，算法通过该误差e(n)值来自动调整自适应滤波器的抽头权向量w(n)，使得下一输出信号y(n+1)与期望信号更接近，从而使得自适应滤波器逐渐收敛并且稳定地工作。图中控制系统是最常用的FIR数字滤波器[14]。基于最速下降法LMS算法迭代公式为[15-16]：

y(n)=wH(n)x(n)

(1)

e(n)=d(n)-y(n)

(2)

w(n+1)=w(n)+2μe(n)x(n)

(3)

式(3)中，μ为步长因子，满足算法收敛的条件是0≤μ≤1/λmax，其中λmax是x(n)的自相关矩阵最大特征值。

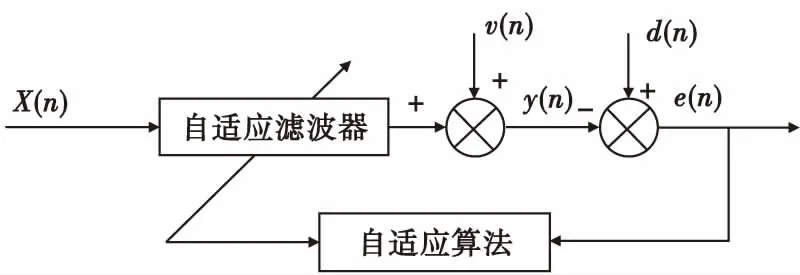
图1 自适应滤波原理图Fig.1 Principle of adaptive filtering

1.2 自适应滤波算法

文献[8]提出的变步长模型：

μ(n)=α(1-exp(-|e(n)|β))

(4)

文献[9]提出的变步长模型：

μ(n)=barctanr(a(|e(n)·e(n-1)|))

(5)

文献[13]中提出的变步长模型：

μ(n)=karctan(a(n)·e(n)m)

(6)

文献[8]提出的变步长模型在稳态收敛阶段有较为缓慢的步长变化，但其曲线还不够平滑，且只考虑了当前误差对步长的影响。文献[9]提出的变步长模型基于反正切函数，在开始收敛阶段具有较大步长，提高了收敛速度，但在稳态收敛阶段，降低稳态误差上有待提高。文献[13]中提出的误差相关函数(α(n)=f(e(n)/e(n-1))2)动态调整步长效果显著。

本文基于对上述文献中的模型优缺点的把握，将文献[8-9]中模型有效结合起来加上文献[13]中的误差相关函数。提出变步长模型，其步长与误差的关系式如下：

μ(n)=k(1-exp(-arctan(α(n)|e(n)2|)))

(7)

α(n)=f(e(n)/e(n-1))b

(8)

2 自适应滤波算法性能分析

2.1 模型参数对滤波性能影响分析

通过步长与误差之间的非线性关系曲线分析变步长函数中参数对算法性能的影响。图2为k，α，f，b取不同值时，步长与误差的关系曲线。从图2可得：

1)k对算法的收敛速度影响较大。初始步长随k的增大而增大，k越大收敛速度越快，k越小收敛速度越慢。

2)α(n)为迭代公式，为了方便分析步长与误差之间的关系，先将α(n)作为常值看待。α对算法的收敛速度的影响与k相似，但其函数形状比k作用下的窄，函数底部变化较快，对收敛速度的影响也较深。

3)f对步长函数的形状以及底部特性影响较大，f值越大曲线向e(n)为0轴越靠拢。f越小曲线底部变化越平缓，即在e(n)等于0附近缓慢变化。

4)b对函数的形状、底部特性和算法的收敛速度影响较为稳定。如图所示在相对较大的范围内其值的大小的改变，作用于函数的变化很小。

综上所述，为了获得较高的收敛速度和较低的稳态误差，需折中考虑变步长函数中参数的取值。

2.2 模型参数的确定

由2.1中通过步长与误差之间的非线性关系曲线分析变步长函数中参数对算法性能的影响。确定k=0.2，α=1较为合理。在α作为e(n)函数时确定f，b的值，仿真条件为：x(n)为高斯白噪声，均值为零，方差为 1；v(n)为高斯白噪声，均值为零，方差为 0.01，且与x(n)不相关；自适应滤波器阶数为2，FIR数字滤波器系数w=[0.8 0.5]T；系统采样点在500时发生时变，为w=[0.4 0.2]T；仿真次数为200，采样点数为1 000时。图3是当函数式(5)中变量b固定取2时，变量f变化对滤波性能的直观描述；其中f取500时其收敛速度最快，稳态误差也最小。

图4在f=500确定后，让b变化观察对滤波性能的影响，通过该图可以看出b在取四个值时的收敛速度几乎一样，但b=0.3时的误差最低。所以，选取b=0.3较为理想。

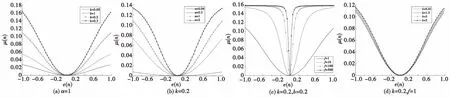
图2 步长与误差关系曲线Fig.2 Relationship curve with error

图3 b=2，f变化时步长与误差关系曲线Fig.3 Relationship curve with error at different values of f

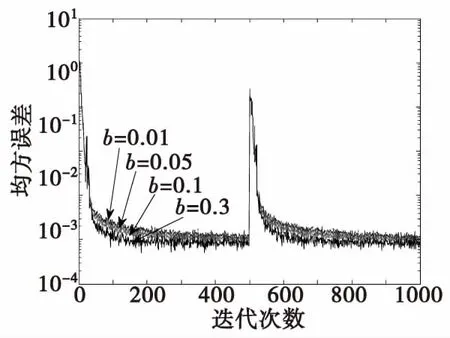
图4 f=500，b变化时步长与误差关系曲线Fig.4 Relationship curve with error at different values of b

2.3 算法滤波性能对比

依据上文分析确定了自适应滤波算法的模型：

μ(n)=0.2(1-exp(-arctan(α(n)|e(n)2|)))

(9)

α(n)=500(e(n)/e(n-1))0.3

(10)

将文献[13]的算法和文献[9]的算法与本文提出的算法，应用于不同信噪比下的高斯白噪声的滤波处理中。文献[9]式(5)的最优值b取0.03，a取800，r取3。文献[13]式(6)的最优值k取0.05，m取2，f取500。

图5仿真结果显示：本文算法在30 dB中具有远低于其他两种算法的稳态误差，在20 dB中的稳态误差远低于文献[9]且收敛速度快于文献[13]。本文算法在处理13 dB和10 dB这样的低信噪比时，在仿真过程中对参数f进行了调整，将其从500调整为5且其余参数值不变，使得总体参数值远低于两个文献中算法参数值，降低了运算量。本文算法在处理低信噪比时，在拥有与文献算法一样的收敛速度的同时具有略低的稳态误差。

图5 本文算法与文献算法在不同信噪比下滤波性能的比较Fig.5 Comparison of filtering performance between algorithm and literature algorithm under different SNR

3 应用实例

本文对文献[17]中所建立的引信回波信号进行分析。其冲击脉冲信号为高斯脉冲信号，时域波形为：

(11)

式(11)中，A0为波形系数，σ=2×10-10。选取其5阶导数高斯脉冲信号作为回波信号，仿真条件设定为：滤波器阶数为15，高频噪声均值为0，方差为0.01，仿真次数200。对比文献[14]中的滤波算法仿真结果如图6—图7所示。

图6 本文算法与文献[13]处理后的回波信号Fig.6 Echo signals after document algorithm and paper’s algorithm processing

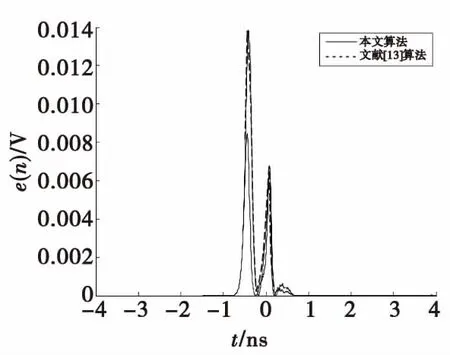
图7 本文算法与文献[13]算法对回波信号的误差性能Fig.7 Error performance of the echo signal from document algorithm and paper’s algorithm

4 结论

本文提出无线电引信回波信号的滤波算法。该算法基于反馈控制函数且将反正切函数和指数函数组合在一起，通过Matlab分析了该算法的滤波性能，并应用于无线电引信回波信号处理中。应用实例表明，本文算法在收敛速度和稳态误差方面均优于文献中所提算法，在高低信噪比时均具有高收敛速度和低稳态误差，且在无线电引信回波信号的滤波处理效果中，本文算法在误差抑制能力上优于原有文献[13]，验证了本文算法的优越性。