基于高度的阻力系数实时修正方法

杨小会，张 英，何江杨，于 良

(1.机电动态控制重点实验室，陕西 西安 710065；2.山东特种工业集团有限公司，山东 淄博 255200)

0 引言

弹道修正是弹药实现精确打击的重要途径，快速准确地预测弹丸落点是实施弹道修正的前提。采用卫星定位进行弹道测量，利用当前弹道参数结合理想的弹道模型外推实际落点是一种常用的落点预测方法[1]，空气动力参数是弹道解算中的关键参数，其中阻力系数又尤其关键，其准确度直接影响落点预测精度。

实测数据表明，高空与地面的空气密度和黏性系数差别很大，导致雷诺数的变化很大，如30 km高空上的雷诺数大约只有地面值的15%[2-3]，这使得弹丸的阻力系数增大，并且随着高度的增加阻力系数增量也越大[4-5]。过去由于弹丸射程小，飞行高度不大，因此弹道解算中直接应用在地面测得的阻力系数，不考虑随飞行高度不同雷诺数变化的影响，解算误差一般不大。然而现代弹丸的飞行距离和高度大为增加，例如155 mm复合增程弹飞行高度可达25～30 km，若不考虑雷诺数对阻力系数的影响则弹道解算误差较大，射程误差可达1%，已不能忽视[6]。

通常雷诺数对于阻力系数的影响采用风洞试验获得，但是只有在可变雷诺数、较高水平的风洞中才能实现，因此不容易获取到不同雷诺数对应的阻力系数。通过空气动力计算软件可以比较容易地获取到不同弹道高度条件下雷诺数对应的阻力系数，可以将雷诺数对阻力系数的修正转换为高度对阻力系数的修正。针对不同弹道高度的气象不同引起雷诺数不同，进而导致阻力系数不准确的问题，本文提出了基于高度的阻力系数实时修正方法。

1 雷诺数对阻力系数的影响

1.1 阻力系数计算方法

弹箭的阻力系数由零升阻力系数和诱导阻力系数组成，零升阻力系数Cx0主要由摩阻系数Cxf、涡阻系数Cxb和波阻系数Cxw组成[7]，见式(1)：

cx0=cxf+cxb+cxw

(1)

在紊流附面层条件下，弹丸的摩阻系数见式(2)：

(2)

式(2)中，Ss为弹丸侧表面积，S为弹丸特征面积，ηλ为形状修正系数，ηm为考虑到空气的压缩性后采用的修正系数。

Re为雷诺数，见式(3)：

(3)

式(3)中，ρ为空气密度，μ为空气的黏性系数，v为弹丸速度，l为弹体长度。

由于目前还没有一个准确的计算涡阻的理论方法，因此采用工程算法[4]，将摩阻和涡阻合在一起计算，见式(4)：

cxf+cxb=Acxf+cxd

(4)

式(4)中，系数A与飞行马赫数和弹丸长细比相关，Cxd为弹丸底阻，其计算方法见式(5)：

(5)

式(5)中，ξ为尾椎收缩比，λB为弹丸长细比，Ma为飞行马赫数。

亚音速时波阻系数为零，超音速时，对于卵形头部和截锥尾部弹丸波阻系数可采用式(6)估算：

(6)

式(6)中，φ0为弹头半顶角，αk为尾锥角。

1.2 雷诺数对阻力系数的影响

由式(1)、式(2)、式(5)和式(6)可知，对于某一弹丸，在同一飞行速度时，不同的弹道高度对应的空气密度和空气黏性系数不同，因此雷诺数不同，相应的阻力系数就不同。图1为不同高度对应的空气密度，图2为不同高度对应的雷诺数，图3为不同雷诺数对应的阻力系数，图4为155 mm榴弹弹丸速度1.2Ma时不同高度对应的阻力系数增量。由图可以看出，高度增加20 km时，空气密度和雷诺数约只有地面的10%，相应的阻力系数增加了10%。

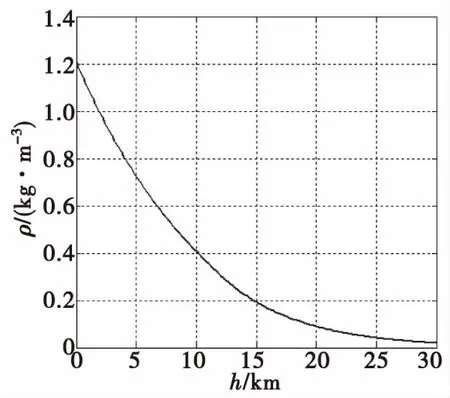
图1 不同高度对应的空气密度Fig.1 Relation between air density and altitude

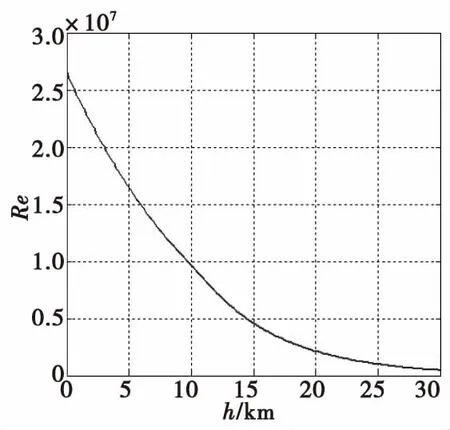
图2 不同高度对应的雷诺数Fig.2 Relation between Reynolds number and altitude

图3 不同雷诺数对应的阻力系数(Ma=1.2)Fig.3 Relation between Reynolds number and drag coefficient

图4 不同高度对应的阻力系数增量(Ma=1.2)Fig.4 Relation between altitude and drag coefficient increment

2 基于高度的阻力系数实时修正方法

2.1 阻力系数与高度的关系

由式(2)和图3可以看出，同一马赫数下，阻力系数随着雷诺数的增大而单调减小，阻力系数是雷诺数的反比例函数，如式(7)：

cx|Ma=g(Re)

(7)

由式(3)可以看出，雷诺数是气象参数即空气密度和黏度的函数，由图1可以看出气象参数是高度的函数，因此，雷诺数也是高度的函数，见式(8)。由图2可以看出，同一马赫数下，雷诺数是高度的反比例函数，即雷诺数随着高度的增加而单调减小。

Re=f(h)

(8)

因此，根据式(7)和式(8)，可以将阻力系数与雷诺数的关系转换为阻力系数与高度的关系，见式(9)。由如图4可以看出，同一马赫数下，阻力系数与高度成正比例关系，高度越高阻力系数越大。

cx|Ma=g(f(h))=k(h)

(9)

2.2 基于高度的阻力系数实时修正方法

图5为155 mm榴弹不同马赫数不同弹道高度对应的阻力系数增量曲线。

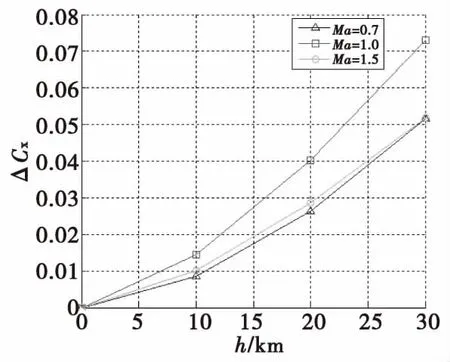
图5 不同马赫数不同弹道高度阻力系数增量Fig.5 Drag coefficient increment of different Ma and altitude

由图5可以看出，同一高度下不同的马赫数弹丸阻力系数增量并不相同，因此不同弹道高度下的阻力系数增量为弹丸飞行马赫数和弹道高度的二元函数，见式(10)：

Δcx(Ma,h)=φ(Ma,h)

(10)

由图5可以看出，同一马赫数下，阻力系数增量与高度近似呈线性关系，因此将同一马赫数下不同高度对应的阻力系数增量进行拟合，可以得到高度与阻力系数增量关系，则式(10)可以变为式(11)：

Δcx(Ma,h)=Kh(Ma)·h

(11)

式(11)中，Kh为相应马赫数对应的高度对阻力系数的修正系数。

通过空气动力计算软件可以计算出地面不同马赫数对应的阻力系数Cx0(Ma)，则不同飞行马赫数不同弹道高度对应的阻力系数见式(12)：

cx(Ma,h)=cx0(Ma)+Δcx(Ma,h)

(12)

3 试验验证

以155 mm底排弹为平台，采用仿真数据验证基于高度的阻力系数修正方法的有效性。

3.1 高度对阻力系数的修正系数获取

采用空气动力计算软件，通过设置不同马赫数、不同高度对应的气象条件计算得到的阻力系数见图6。将地面阻力系数作为基准，计算的不同高度对应的阻力系数增量，进而得到高度对阻力系数的修正系数。修正系数的拟合采用万米为单位，公式如下：

Δcx(Ma,h)=Kh(Ma)·h/10 000

(13)

拟合结果见表1。

表1 高度对阻力系数的修正系数Tab.1 Drag coefficient modified coefficient of altitude

图6 不同马赫数不同弹道高度阻力系数Fig.6 Drag coefficient of different Ma and altitude

3.2 仿真验证

以155 mm底排弹为平台，在初速933 m/s，射角52°，4 500 m海拔气象条件下(射程约55 km)，分别采用地面阻力系数和基于高度实时修正的阻力系数解算弹道，弹道曲线见图7。由图可以看出，基于高度实时修正的阻力系数解算的射距较采用地面阻力系数解算的射距近1 198 m，约2.14%，横偏近43 m，约1.97%。

图7 不同阻力系数解算的弹道曲线Fig.7 Trajectory of different drag coefficient

3.3 试验验证

基于155 mm底排弹全装药最大射程角外场试验雷达跟踪数据和实测气象数据，分别采用地面阻力系数和基于高度实时修正的阻力系数，从弹道顶点时刻开始预测弹丸的落点坐标，将预测的落点坐标与实测的落点坐标进行比较，计算预测误差，评估基于高度的阻力系数修正方法的有效性。弹丸的落点坐标见图8。

由图8可以看出，从弹道顶点时刻开始弹丸落点预测，采用地面阻力系数预测的落点误差较大，5发弹丸射距误差均值为87.2 m，横偏误差均值为62.0 m；基于高度实时修正的阻力系数预测的落点误差较小，射距误差均值为31.4 m，横偏误差均值为19.6 m，预测精度约提高了一倍。

图8 弹丸落点坐标Fig.8 Impact point of projectile

4 结论

本文提出了基于高度的阻力系数实时修正方法。该方法通过空气动力计算软件获取到同一马赫数不同高度气象条件对应的弹丸阻力系数变化量与高度的对应关系，在弹道解算中，采用弹丸实际弹道高度插值该关系，实现了弹丸阻力系数的实时修正。155 mm榴弹底排弹最大射程角验证结果表明：4500 m海拔时，高度修正的阻力系数对弹丸的射距和横偏影响可达2%；从弹道顶点时刻开始弹丸落点预测，采用修正后的阻力系数较采用地面阻力系数的落点预测精度约提高了一倍。