Automated p ebble mosaic stylization of images
2019-05-14LarsDoyleForestAndersonEhrenChoyandDavidould
Lars Doyle(),Forest And erson ,Ehren Choy ,and David M ould
Abstract Digital mosaics have usually used regular tiles,simulating historical tessellated mosaics.In this paper,we present a method for synthesizing pebble mosaics,a historical mosaic style in which the tiles are rounded pebbles.We address both the tiling problem,of distributing pebbles over the image plane so as to approximate the input image content,and the problem of geometry,creating a smooth rounded shape for each pebble.Weadopt simplelinear iterativeclustering(SLIC)to obtain elongated tiles conforming to image content,and smooth the resulting irregular shapes into shapes resembling pebble cross-sections.Then,we create an interior and exterior contour for each pebble and solve a Laplace equation over the region between them to obtain height-f ield geometry.The resulting pebble set approximates the input image while representing full geometry that can berendered and textured for a highly detailed representation of a pebble mosaic.
Keyword s non-photorealistic rendering;digital mosaics;image stylization;segmentation;image processing
1 Introduction
Mosaics are an art form that date back thousands of years.The earliest historical mosaics were pebble mosaics[1,2],whose component pebbles were heterogeneous in size and shape.Pebble mosaics paved f loors with pebbles,arranged so as to form an image or design.The craft of pebble mosaics continues into the 21st century[3]with new pebble mosaics being built by hobbyists and city planners.Pebble mosaics,as well as the contemporaneous chip mosaics made of fragments of quarried stone[1],use entirely irregular tiles.The archetypal mosaic is the tessellated mosaic,made of regular cubes of stone(tesserae).Such tessellated mosaics are the most familiar kind of mosaics and have been the most thoroughly studied in computer graphics.Tessellated mosaics have been dated to the third century BCE.However,pebble mosaicsappeared in Greece hundreds of yearsearlier[1]and havenot received much attention in computer graphics.In thispaper,weproposea novel algorithm for constructing irregular pebble mosaics,using a variant of simple linear iterative clustering(SLIC)[4]to obtain an initial segmentation,smoothing the resulting boundaries,and using a Poisson solver to interpolate a smooth height field for each pebble which we can then render using conventional lighting and texturing.
For a mosaic to successfully convey an image,it is important to align tile edges with image edges.The use of square tiles imposes severe restrictions on the detail level that can be captured;our irregular tiles can convey considerable detail,including interior edges of f igures,something often neglected in previous techniques.Our algorithm isentirely automatic;users can optionally guide the output by annotating the input image with an importance map or by manually adding decorative features in a preprocessing phase.

Fig.1 Fragment of a pebble mosaic f loor dating from the 4th century BCE.

Fig.2 An image progressing through our system.Left to right:input,segmentation,boundary smoothing,pebble geometry,lighting.
This paper makes two main contributions.Firstly,we adapt SLIC so that it is suitable for creating irregular,elongated pebble shapes.We estimate the local direction of the image and then bias the SLIC clustering distance according to a local coordinate system,producing natural-looking size and aspect ratio variations.Secondly,we compute smooth pebble geometry for the resulting tiles.We use the Laplace equation,setting up constraints and then solving to meet them,to produce smooth shapes resembling river pebbles.By creating and rendering this geometry,we bridge photorealism and non-photorealism.
This paper is organized as follows. Section 2 reviews previous work on computer-generated mosaics.Section 3 describes our algorithm in detail.Section 4 shows images created using our method and discusses its benef its and drawbacks.Finally,Section 5 summarizes the work and suggests future directions.
2 Related work
Battiato et al.[5]proposed a taxonomy of digital mosaic research in which the two initial branches divide tile mosaics from multi-picture mosaics.This distinction stems from the nature of the basic picture elements.In tile mosaics,the image plane is divided into small regions,each individually colored to represent the underlying input image.In contrast,multi-picture mosaics employ a dataset of images that are used to assemble an approximation to the input image based on local color and structure similarity;the typical result is a photomosaic[6].We situate our current work within the tile mosaic branch.
In the seminal Paint by Numbers[7],Haeberli introduced many of the concepts that have since been used for mosaic emulation.His idea of using Voronoi diagrams for mosaics has been used in commercial products and in subsequent research;centroidal Voronoi diagrams(CVDs)are particularly common.CVDs are often produced by Lloyd’s algorithm,a relaxation process that repeatedly moves the Voronoi centres to the centroids of their regions.The CVD process has formed the basis for much work in mosaic and stipple creation[8–10],since it is a good way to distribute points on the plane.
Hausner[8]presented an iterative algorithm for placing mosaic centres,using hardware-accelerated CVDs to distribute tiles.Hausner also identif ied a crucial issue in mosaics:tile edges should be aligned with image edges.Hausner resolved this in his work by having tiles move away from user-specif ied edges.An alternative method for achieving edge alignment was given by Elber and Wolberg[11],who arranged rows of tiles along streamlines parallel to initial userspecif ied curves.Yet another way of addressing edge alignment was given by Di Blasi and Gallo[12],who proposed to cut the rectangular tiles where they cross image edges.Liu et al.[13]used graph cuts rather than explicit edge detection to prevent tiles from crossing image edges.
Within the multi-picture mosaic branch a thread of research involves populating a set of container shapes with tiles,generally without any intention of providing interior image detail.Kim and Pellacini’s Jigsaw Image Mosaic[14]is an example,where the method producesan irregular tiling of theimageplane with predef ined tiles,minimizing a set of error criteria including tile overlap and color mismatch.More recent work by Saputra et al.[15,16]arranges f igures within the container shape while seeking an aesthetic distribution rather than a full packing.Kwan et al.[17]accelerated partial-shape matching,through their pyramid of arc-length descriptor,for packing irregular shapes.
Other methodsfor distributing primitivesand tiling the plane have been devised,and we brief ly mention a few others.Smith et al.[18]focussed on coherent movement of tiles to create animated mosaics;later,Dalal et al.[19]used Fourier transforms to f ind good packings of input primitives.Kaplan and Salesin[20,21]worked on automatically controlling tile shapes to produce Escher-like tilings in which the tiles were close to an input goal shape.Similarly,Goferman et al.[22]extracted irregular regions of interest from a seriesof photographsand packed them in a puzzle-like manner within a chosen aspect ratio.Photo collage is a related area,but removes the constraint that an underlying image or containing shape must be represented.Using convolutional neural networks,Liu et al.[23]produced photo collages by grouping together images with similar content over the image plane.
3 Constructing p ebble mosaics
In our approach,we tile the image plane using heterogeneous,3D pebble-shaped objects. As in previous methods[8,11,12],our tiles avoid crossing image boundaries and are oriented to align with a direction map.However,we take a dif ferent approach towards this goal. Section 3.1 describes how we modify the simple linear iterative clustering(SLIC)algorithm[4]to produce oriented pebble shapes.We take advantage of the inherent boundary-avoiding quality of SLICand thushaveno need for explicit edge detection nor associated parameters or thresholds.We describe how we simplify the boundaries of the initial segmentation in Section 3.2 to produce smooth,“river-worn”pebbles. Finally,in Section 3.3 we construct a height f ield from the 2D boundaries to extend pebbles into 3D,before applying lighting to the resulting geometry.A schematic representation of our algorithm pipeline in Fig.3 shows how an input image I is transformed into a pebble mosaic.
3.1 Segmentation
SLIC produces compact super-pixels by clustering pixels into groups,based on colour and spatial distance. Their tendency to adhere to image boundaries is benef icial for describing image content and forms the basis of our pebble shapes.In its original formulation,the spatial distance of a pixel p from a cluster center c can be described by an of fset vectorv=p−c,allowing us to compute the l2distance as

where vxand vyare the components ofv parallel to the x-and y-axes.It is often the case in nature that pebbles are longer in one dimension than the other,forming approximate,oval-like boundaries as opposed to circular ones.As a f irst modif ication to Eq.(1)we can apply dif ferent scaling factors to the x and y components ofv.This results in the elongated super-pixels that are shown in the top right image of Fig.4.
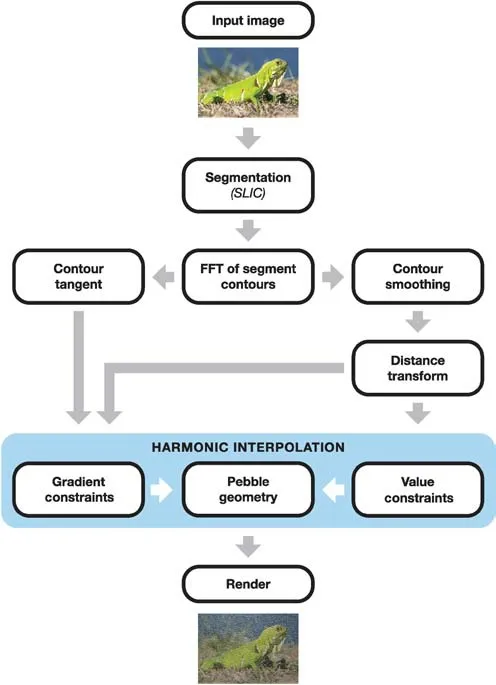
Fig.3 Pipeline of our proposed method.
Artists often take advantage of pebble shapes and will emphasize image edges by aligning the long side of a pebble parallel to an edge.We can approximate this ef fect with one further modif ication to our distance metric.First,we construct a structure tensor[24]at each super-pixel center by integrating the matrix f ield,∇I∇IT,weighted by a Gaussian function.The tensor’s unit eigenvectors e1and e2,associated with eigenvaluesλ1λ2,are parallel and perpendicular to the smoothed image gradient.We can now use these vectors as a new basis in our distance calculation.Furthermore,applying a larger weight to the component ofv parallel to e1than e2allows super-pixels to spread tangent to image edges.This ef fect can be seen in Fig.4(bottom left).In f lat or corner regions,where there is inadequate orientation information,we simply assign a default direction.This assessment is made by thresholding an orientation coherence estimate:

Fig.4 Top left:original SLIC.Top right:scaling v y in Eq.(1)by α=3.Bottom left:scalingv·b1 in Eq.(3)byα=3.Bottom right:using random scaling in Eq.(3).
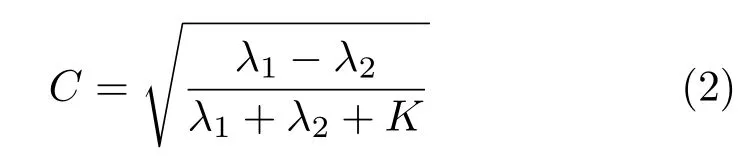
where K is a constant chosen to avoid division by zero and to de-emphasize weak tensors.
The f inal distance metric is
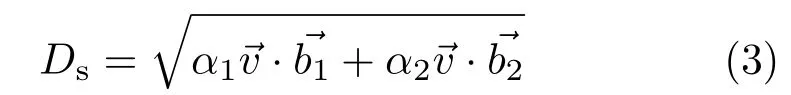
whereα1andα2are scaling factors,controlling both the aspect ratio and the overall size of each cluster.The vectorsb1andb2correspond either to the local image orientation,if a strong local orientation exists,or a default direction. The decision is made by comparing C to a threshold Tcohas follows:
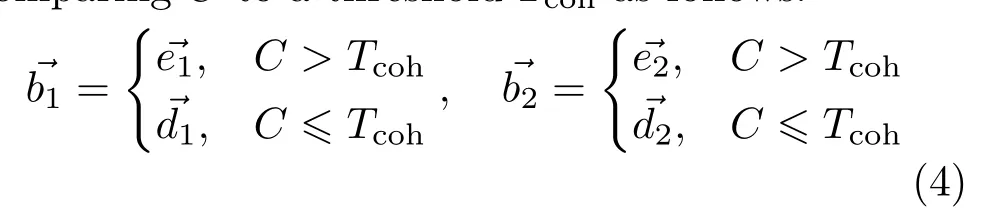
The vectors d1and d2comprise a default orthonormal basis.In our examples we set Tcohto 0.5 and d1to the y-axis.
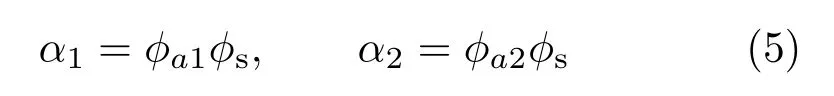
The scaling factorsα1and α2are selected individually for each super-pixel guided by a random process,such that Through experimentation,we chose to compress the aspect ratio perpendicular to edges byφa1=3.The other terms are determined by two uniform random numbers r1,r2∈[0,1].We then setφa2=(φa1−1)r21+1 and set the scale termφs=r22+1.
The local distance metric Dsis used in the SLIC process to oversegment the image. We refer to the resulting oversegmented image as P,and each segment,Pi∈P,is a pebble.
3.2 Bound ary smoothing
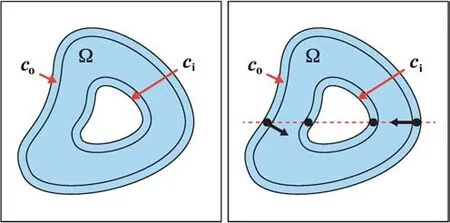
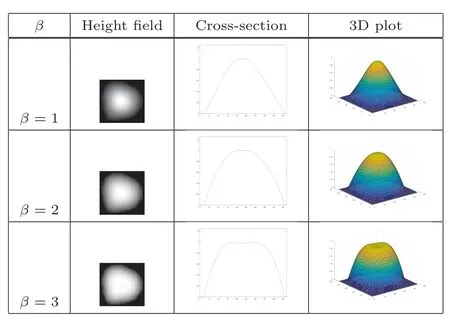
The pebbles constructed in Section 3.1 contain many irregularities that depart from the smooth pebble shapes that we wish to create.Hence,we apply a low-pass f ilter in the frequency domain[25]to each pebble’s outer contour co(k),for k=0,1,···,K−1.This process ef fectively reconstructs a contour from L Fourier coef ficients,where L Fig.5 Left to right:original contour,and reconstructed contours using L=37,17,and 7 Fourier coef ficients. Fig.6 High-resolution pebbles rendered at 5 times the input resolution.Left:pebble shapes.Right:3D rendered pebbles. We construct a height field for each pebble by means of harmonic interpolation over the domain,Ω,that resides between two contours(Fig.7(left)).The outer contour,co,is described above.We obtain the inner contour,ci,by thresholding the normalized distance transform of Piby Tdist∈(0,1).We set a zero gradient at the inner contour,thus creating a small flat face to each pebble which then curves downwards to the image plane.In all examples,we set Tdist=0.85. Our height f ield is the solution to the Laplace equation[26]: with boundary value constraints Pi|co=0 and Pi|ci=1.Additionally,we set gradient constraints at the boundariessuch that|∇Pi|=0 on ci.Thegradient on cois constructed as follows.Returning to the Fourier transform of Section 3.2,we note that the derivative co(k)of the sampled function co(k)can be computed in the Fourier domain.This process provides us with a sequence of vectors that are tangent to the curve,one for each sample point.Rotating each vector 90◦inwards gives us a gradient orientation that is orthogonal to the boundary.The gradient magnitude is chosen as follows: where Dmaxis the maximum value of the distance transform.The parameterβdetermines the shape of the resulting pebble;various settings are illustrated in Fig.8.We chooseβ=2 to construct the pebble prof ile curving downward into the surrounding area in our examples.Notice that settingβtoo high results in the gradient overshooting its target at the inner contour resulting in a depression at the center as seen in the bottom row of Fig.8. Fig.7 Left:the domain,Ω,and boundaries(c o and c i)of P i.Right:the gradient orientation on c o(arrows)and zero-gradient on c i(dots). Fig.8 Constructing a height f ield at varying scales of gradient magnitude on c o. We apply Phong shading to the resulting height f ield.We use the average colour in I under Pias the pebble’s surface color.Optionally,we can apply a rock texture to the pebble as well.The texture image is randomly sampled for each pebble and combined with the luminosity channel using a multiply blend.Example mosaics produced using this scheme,with and without texture,are shown in Figs.9(above)and 9(below)respectively. Fig.9 Above:result without texture.Below:textured result. We demonstrate our method on photographs containing various subject matter in Fig.10,using 2000 pebbles in each example.The original source images are shown in Fig.20.Rendering time for a 1.5 megapixel image is 28 s using our unoptimized CPU implementation.The majority of this time(25 s)is spent solving 2000 N2isparse linear systems in order to construct the geometry of the pebbles.Increasing the pebble count leads to solving smaller matrices and thus faster execution time;for example,using 3000 pebbles reduces the solving time to 16 s. Notice that even at this coarse scale,most of the important image features are still recognizable.The elongated pebble shapes add an impression of motion to the results.This is most noticeable in the cat image at the top left where the pebbles follow the fur orientation.In the portrait image(second row,left)we see how random pebble scaling can add visual interest to otherwise f lat image regions.Thisbringsto mind the activity of a mosaicist using tiny pebbles to f ill the empty spaces left between larger stones.In the bottom row,adding texture supports the transition from the synthetic 3D shapes in the top rows to a more natural-looking material. Fig.10 Results.Top two rows:without texture.Bottom row:using marble texture. Inspired by historical mosaics,such as the one depicted in Fig.1,we demonstrate our method on the ornamental designs shown in Fig.11.Due to the high contrast in these images,the pebbles adhere well to the image content,creating a striking rerepresentation of the input. Our system has f ive notable degrees of freedom that can inf luencetheoutcomeof thef inal rendered mosaic:color,shape,texture,orientation,and size.Webrief ly discuss each here. Color.Following the tradition in tile mosaics[7,8,11,12]we render each pebble with the average color under the corresponding image region.Alternatively,we could allow color to vary over the pebble region,guided by the input image. Shape.Pebble shape can be inf luenced by the lowpass f ilter used in the smoothing process discussed in Section 3.2 and illustrated in Fig.5.We chose to retain seven Fourier coef ficients,resulting in smooth oval-like pebble shapes.However,less smoothing would provide more shape variety. Texture. We currently limit pebble texture to a single sample but there is potential for more development along this dimension.For example,a database of texture swatches could be employed to match pebble texture with the underlying image.This addition would provide further connection with the input image and increase recognizability. Fig.11 Results for ornamental motifs.Left:input images.Right:results. Orientation.Pebbles are oriented parallel to image edges,as is common in both traditional and digital mosaics[8,11,12].As explained in Section 3.1,we determineorientation through a structure tensor f ield,defaulting to a f ixed orientation where inadequate information is present.We could also ask the user to provide a vector f ield in place of a single default direction. Size. We discuss pebble size in the following subsections,f irst talking about local variation in pebble dimensions and then discussing size more generally,including the option of varying pebble size based on an importance map. 4.1.1 Pebble dimensions In Section 3.1 and Eq.(5)we describe a random process that determines the aspect ratio and relative size of individual pebbles.We now show how varying these parameters can inf luence the resulting mosaic;the images in the top row of Fig.12 provide a visual example.In Fig.12(top left)we f ixφs=1 to maintain a constant scale and vary the aspect ratio using a random number.Here we increase φa1to 5 and calculateφa2as before. The long thin pebbles work well in this situation where we connect them with the cat’s fur. Compare this result to the cat in Fig.10.There,settingφa1to 3 shows less movement in the cat’s fur,but randomly changingφsbrings out more variation and liveliness.In Fig.12(top right),we f ix the aspect ratio to φa1=φa2=1 and allow the scale parameter to vary.We setφs=5r2+1,where r is a uniform random number in[0,1].Without orientation information it is more dif ficult to identify the image.Also,such extreme variability in pebble size is distracting since the sizes are chosen randomly rather than based on image content.In Fig.12(bottom,left and right)we demonstrate the impact of the random factors in the scaling parameters:note the dif ferent outcomes for two runs,using identical parameters. Fig.12 Top left:randomly varying pebble aspect ratio,f ixed scale.Top right:randomly varying pebble scale,f ixed aspect ratio.Bottom:rendering is nondeterministic due to random scale parameter. 4.1.2 Pebble size In Fig.13 we vary the number of pebbles that make up a mosaic image.On the left we see a detailed result using 3000 pebbles.Many traditional mosaics,such as the one depicted in Fig.1,were constructed with this high level of detail.Next,we see a result using 1000 pebbles.Even at this larger size,much of the image remains clear owing to SLIC’s tendency to adhere to image boundaries.Finally,the pebble size on the right has probably been pushed too far,making it dif ficult to recognize the main f igure in the result.See Fig.15 for a rendering of this image using 2000 pebbles. We can also vary the pebble size by use of an importance map.The mask in the inset of Fig.14 indicates regions to be rendered with smaller,more numerous pebbles. This technique is useful for drawing attention to important regions and provides a more detailed representation of the content. Fig.13 Varying pebble size.Left to right:3000,1000,500 pebbles. Fig.14 Pebbles within the important area(inset)are rendered at a higher frequency. Figure 15 shows a comparison between our method and Hausner’s[8]using 2000 pebbles.Here,we turn of fthe lighting ef fects and make the comparison based on tile shape alone.(The color shift between the two examples is due to using dif ferent source photographs of the painting).By using heterogeneous shapes,image content can be more accurately portrayed than when using an equal number of 2D homogeneous primitives.In our result,the pebble shapes cleanly outline the contours of the f igure and its drapery.Where smaller pebbles are needed to f ill an image region,our method is not restricted to a uniform pebble size.Both these properties stem from our use of SLIC as the initial segmentation method.Of course,both our method and Hausner’s can use smaller primitives in regions specif ied by users. Similarly,we compare our method with three previous tile mosaic algorithms on a common image in Fig.16. Our result is on the bottom right using 3000 pebbles.At the top left,Di Blasi and Gallo[12]obtain clean lines and uniform spacing by cutting tiles that overlap perceptual guidelines and neighbouring tiles.The edges in our rendering are obtained through SLIC which adhere well to step edges but fail when perceptual boundaries are not matched with a strong color discontinuity.An example can be seen in the thin strand of feathers above the brim of Lena’s hat where pebbles are not constrained to this narrow region.This is a case in which perceptual edge detection would benef it our segmentation.Schlechtweg et al.’s[27]Render Bots show f ine detail by using 9000 primitives but the placement is uneven and rendering took one hour to complete. Fig.15 Comparison.Left:Hausner’s method.Right:ours.Both results use 2000 tiles Fig.16 Comparison with previous tile mosaic algorithms. Recently,there has been much attention given to using convolutional neural networks for image stylization[28,29].In Fig.17(center)we show a result obtained from deepart.io,a popular online implementation of Gatys et al.’s method[28].The high-level semantic features used in neural style transfer preserve image features better than the lowlevel color features that we use;compare the detail images in Figs.17(bottom left)and 17(bottom right).The iguana’s eye clearly highlights the advantage of using semantic features:style transfer reproduced the eye using a single pebble,improving recognizability.Our method,in contrast,uses a number of pebbles dependent on the SLIC super-pixel size;it artif icially breaks the eye into three pebbles.The advantage of our method lies in explicitly modeling pebble shapes.The texture produced by neural style transfer in Fig.17(center)only roughly approximates that found in the style example in Fig.17(top left).For example,the def inition of individual pebbles is completely lost in parts of the background and the side of the iguana’s head.In contrast,our method explicitly models individual pebble geometry and can output well-def ined shapes at any resolution. Our method performs best on images with high contrast and clear distinctions between regions of dif fering semantic content.Due to the relatively large scale of the pebbles,some subtle image features or tiny details can be lost.Figure 18(top)shows an image dominated by high-frequency content.In our rendering in Fig.18(right),only a large-scale impression of the scene is captured. Reducing pebble size is only a limited option since,past a certain scale,the cement between the pebbles will feature as prominently as the pebbles themselves.In Fig.18(bottom)the facial features are poorly represented.SLIC does not ef fectively cope with lighting changes in the area of the man’s nose,for example.Either more sophisticated low-level processing or learning-based semantic segmentations could improve on our results,and both are promising directions for future work. Fig.17 Comparison with neural style.Top left:style example.Top right:input image.Center:pebble mosaic rendered with neural style[28]as implemented at deepart.io.Bottom left:detail.Bottom right:detail of Fig.9(bottom). Continuing our discussion on color,we also note that our resulting images would be dif ficult to recognize based on pebble layout only.See Fig.19 for an example of a black and white pebble layout.Without colorization,the orientation and pebble boundaries only hint at the underlying image.More work could be done to emphasize the structural content of the image by varying pebble shape and size,linking size and shape variation to image content instead of varying pebble dimensions with random factors.At the same time,it might be possible to improve our pebble colors.Because we add lighting ef fects to a base color derived from the image,the f inal pebble color distribution is not necessarily very close to the desired color.We could improve the mosaic by better integration of the lighting process and the selection of base color. Fig.18 Limitations of our method.Top:high-frequency features.Bottom:semantic content. Fig.19 Pebble layout without colorization. Processing time is also an issue. Our main bottleneck is determining the numerous matrices that construct the height f ield.Taking advantage of parallelization would help.Also,solving at a lower resolution and smoothing the results could improve timing. Fig.20 Input images used in Figs.9,10,13,14,and 15. Although we think that smooth river-worn pebbles are the most commonly type used for pebble mosaics,more varied rock types in principle could be used,and this paper did not attempt to treat these. In thispaper wepresent a method to render 3D pebble mosaics.Digital mosaics have been presented in the NPR literature previously,but only in the context of tiling a 2D surface;here,we not only create a tiling representing pebbles,but also generate a height f ield for the pebbles so that they can be rendered. Our method starts by segmenting the image plane with SLIC,equipped with a modif ied distance metric.Theresulting super-pixels adhereto image boundaries and hence no further edge detection is required.By varying the size,orientation,and aspect ratio of the super-pixels,we obtain pebble shapes that are highly expressive in their depiction of image content. We construct the geometry of each pebble by solving a Laplace equation on the domain between two contours.The resulting height f ield can then be rendered using a variety of lighting techniques beyond the simple Phong shading model we use in this paper.In addition,since we have synthesized 3D geometry,our pebble mosaics can be used in novel applications,from 3D virtual environments to physical 3D printed objects. In the future we would like to use semantic segmentation to improve the initial super-pixel clustering. Important image regions,especially on the human face,could benef it by constraining clustering to regions of similar content.Better use of low-level image features could improve on the SLIC segmentation.Pebble texture could also be customized to suggest image details at a scale below the size of individual pebbles.This addition would bridge the gap between tile and multi-picture mosaics,as def ined by Battiato et al.[5],and strengthen the connection between the original image and its mosaic representation. Acknowledgements We would like to thank the anonymous reviewers for many insightful comments.Wealso thank membersof the Graphics,Imaging and Games Lab for productive comments and discussions.Funding for this work was provided by NSERC,OGS,and Carleton University. We used many images from Flickr under a Creative Commons license.Thanks to the numerous photographers who provided material:Douglas Scortegagna(landscape),bDom(b&w portrait),Julio Romero(iguana),Peat Bakke(t-rex),G´abor Lengyel(portrait),Tommie Hansen(canal),Theen Moy(cat),JB Banks(dark woods),Richard Messenger(Yemeni),Greg Myers(tomatoes),sicknotepix(toque).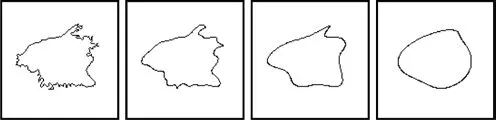

3.3 Pebble geometry
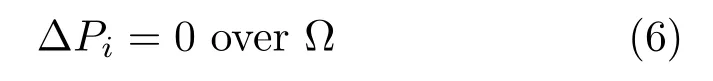
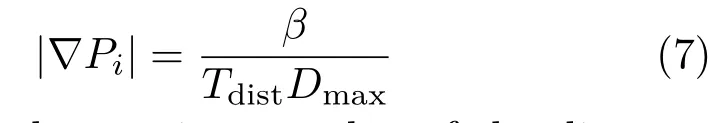
3.4 Rendering

4 Results and discussion

4.1 Degrees of freedom




4.2 Comparison with related work


4.3 Limitations




5 Conclusions
杂志排行
Computational Visual Media的其它文章
- Shadow GAN:Shadow synthesis for virtual objects with conditional adversarial networks
- Recurrent 3D attentional networks for end-to-end active object recognition
- Image-based app earance acquisition of ef fect coatings
- Real-time stereo matching on CUDA using Fourier descriptors and dynamic programming
- Discernible image mosaic with edge-aware adaptive tiles
- Removing fences from sweep motion videos using global 3D reconstruction and fence-aware light f ield rendering
