水下压电智能结构振动控制中传感器/作动器位置优化

2019-05-14张万良熊晨熙

船舶力学 2019年4期

安方，张万良，段勇，熊晨熙

（中国船舶科学研究中心船舶振动噪声重点实验室，江苏无锡214082）

0 引言

水下结构振动是引起水下声辐射的主要原因，研究水下结构振动的主动控制技术能有效解决水下结构减振降噪问题。而性能优良的主动控制器，依赖于传感器与作动器能够发挥最大的效能，这就需要建立有效的优化模型及优化准则。水下压电智能结构需要考虑压电作动、传感功能[1-2]及流体加载效应[2-3]，具有压电—流体—结构三场耦合复杂特性[2]，优化模型及优化准则难于建立，导致水下压电智能结构的传感器/作动器位置优化问题难以解决。

依赖于Abaqus 软件建立的有限元模型，能够基本反映压电—流体—结构三场耦合复杂特性[2]。但由于耦合模型维数较高，无法作为优化模型进行传感器、作动器的位置优化。文献[4]基于有限元模型，对水下压电智能壳体结构振动采取了主动控制方案，但未对其传感器/作动器进行优化配置。文献[5]虽然对传感器/作动器进行了优化配置，但是针对的是空气中的简单模型，不适用于水下智能结构这种复杂模型。因此，水下压电智能结构的传感器/作动器优化，需要首先解决水下智能结构的优化模型建立问题，再解决优化准则问题，从而最终获得压电传感器/作动器的最佳粘贴位置。

本文针对以上两个问题，搭建了水下智能结构的Abaqus-Matlab 联合建模平台，获得考虑压电—流体—结构三场耦合特性的低维优化模型。基于此优化模型，建立基于能量传递的作动器、传感器位置优化准则，最终获得传感器、作动器的最佳粘贴位置。以粘贴有压电纤维（Micro Fiber Composite，简称MFC）作动器/传感器的压电圆柱壳为研究对象，通过相同激励信号下，不同配置位置的水下压电智能圆柱壳振动能量传递的大小，验证了优选位置的合理性。

1 研究对象

本文研究如图1 所示的压电智能圆柱壳体水下振动控制中传感器与作动器的位置优化问题。所采用的作动器为可粘贴于曲面结构的MFC（见图3），圆柱壳主体尺寸及压电纤维尺寸见图2 及图3。圆柱壳上粘贴4 片MFC，一片用作激励，两片用作作动，一片用作传感。在位置优化之前，先假定4 片压电片粘贴在圆柱壳中间位置，呈等角分布（图4），其中，压电外激励作动器放置在圆柱壳中间位置，不作优化。

图1 压电圆柱壳水下模型示意图Fig.1 Underwater model of piezoelectric cylindrical shell

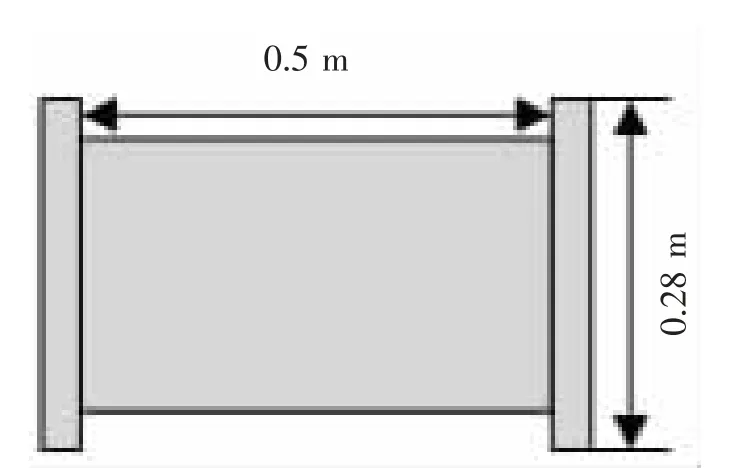
图2 圆柱壳尺寸Fig.2 Cylindrical shell size

图3 MFC 实物图和MFC 尺寸Fig.3 MFC and its size

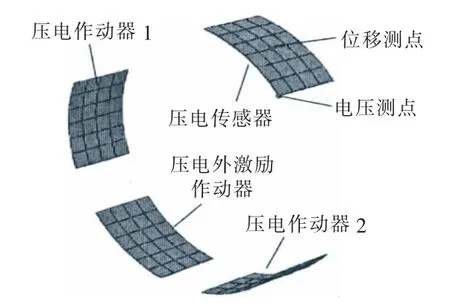
图4 未优化前作动器/传感器分布位置及电压/位移测点分布位置Fig.4 The unoptimal position of the actuators/sensors and voltage/displacement measurement points

2 优化模型建立方法

2.1 压电—结构耦合动力学模型

考虑压电电势自由度的机电耦合有限元模型的振动方程具有如下形式[2，6-8]：

式中：自由度u 与v 分别为结构的广义位移自由度和压电结构的电势自由度；Ms，Cs，Ks分别为结构的质量、阻尼、刚度矩阵；Kp与Ksp分别为压电结构的刚度矩阵及结构与压电耦合的机电耦合刚度矩阵；Fv为施加在结构上的外力矩阵；Qp为电荷矩阵。

压电—结构耦合的动力学方程具有（1）式所示的形式。由此式可以看出，压电的存在只影响到刚度矩阵，质量、阻尼矩阵只在结构处存在非零元素，其余位置为零元素。当借助有限元软件建立压电圆柱壳的有限元模型时，软件内部会自动产生刚度、质量和阻尼矩阵，若能够从中提取出来，便可获取到压电圆柱壳的动力学方程。

图5 压电圆柱壳体整体阻尼矩阵Fig.5 Global damping matrix of the piezoelectric cylinder

图6 压电圆柱壳体整体刚度矩阵Fig.6 Global stiff matrix of the piezoelectric cylinder

图7 压电圆柱壳体整体质量矩阵Fig.7 Global mass matrix of the piezoelectric cylinder

图8 压电圆柱壳有限元模型和优化模型电压、位移对比Fig.8 Voltage and displacement comparison between the finite element model and optimal model for the piezoelectric cylindrical shell

图9 压电圆柱壳有限元模型与优化模型扫频激励输出电压对比Fig.9 Voltage comparison in frequency domain between the finite element model and optimal model for the piezoelectric cylindrical shell

基于Abaqus-Matlab 联合建模平台，首先获取Abaqus 建立的压电圆柱壳有限元模型，圆柱壳部分赋壳单元S4R 属性；MFC 应用压电体单元C3D8E属性。基于Abaqus 建立的有限元模型，提取结构的刚度、质量和阻尼矩阵，基于这些数据信息，在MATLAB 中组装矩阵阻尼、刚度和质量矩阵。在组装过程中，将9 自由度改写为7 自由度，按照位移自

2.2 流体—压电—结构耦合动力学模型建立方法

表1 压电圆柱壳有限元模型与优化模型频率对比（单位：Hz）Tab.1 Frequency comparison between the finite element model and the optimal model for piezoelectric cylindrical shell(Unit：Hz)

继续考虑流体单元，建立流体—压电—结构的耦合动力学模型。基于以上压电圆柱壳有限元模型（1），考虑水的作用，在流固耦合方程中，采用流场压力p 作为水的基本未知量，得到机—电—流耦合动力学方程为[2]

其中

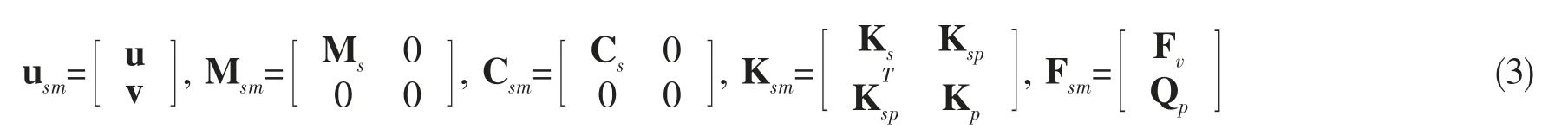
压电—结构耦合的动力学方程具有（1）式所示的形式，而流体-压电-结构耦合的动力学方程具有（2）式所示的形式。由此式可以看出，流体的存在只影响到结构的质量、刚度矩阵，在右下角处的Mf、Kf为流体的质量、刚度矩阵。（2）式中刚度矩阵的右上角及质量矩阵的左下角-Ssf处为非零阵，两者互为转置，且相差一个负号，代表流体与结构的耦合质量、刚度矩阵。阻尼矩阵只在结构处存在非零元素，其余位置为零元素。pf为流体加载力。这是有限元所建立的流体—压电—结构耦合动力学方程。

图10 水下压电圆柱壳整体阻尼矩阵Fig.10 Global damping matrix of the piezoelectric cylinder submerged in water

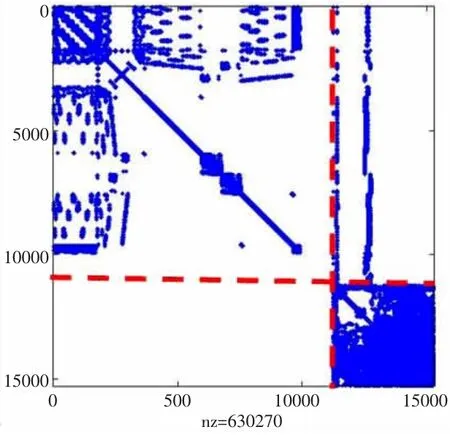
图11 水下压电圆柱壳整体刚度矩阵Fig.11 Global stiff matrix of the piezoelectric cylinder submerged in water

图12 水下压电圆柱壳整体质量矩阵Fig.12 Global mass matrix of the piezoelectric cylinder submerged in water

基于Abaqus-Matlab 联合建模平台，首先提取Abaqus 模型中的阻尼、质量和刚度信息，分析出结构矩阵信息，在MATLAB 中组装阻尼、质量和刚度矩阵，见图10～12。在组装过程中，将9 自由度改写为7 自由度，按照位移自由度电势自由度v=及压力自由度的顺序排列。图10～12 与理论模型（2）中的质量、刚度矩阵的形状完全一致。由此说明组装矩阵的结构形式是正确的。又由表2 中计算的前5 阶频率可验证组装有限元模型的刚度、质量矩阵的有效性。再进一步由时域及频域的响应（图13 和图14），可验证阻尼矩阵、作动和传感矩阵的正确性。

表2 水下压电圆柱壳有限元模型与优化模型频率对比（单位：Hz）Tab.2 Frequency comparison of the finite element model and optimal model for piezoelectric cylindrical shell submerged in water(Unit：Hz)

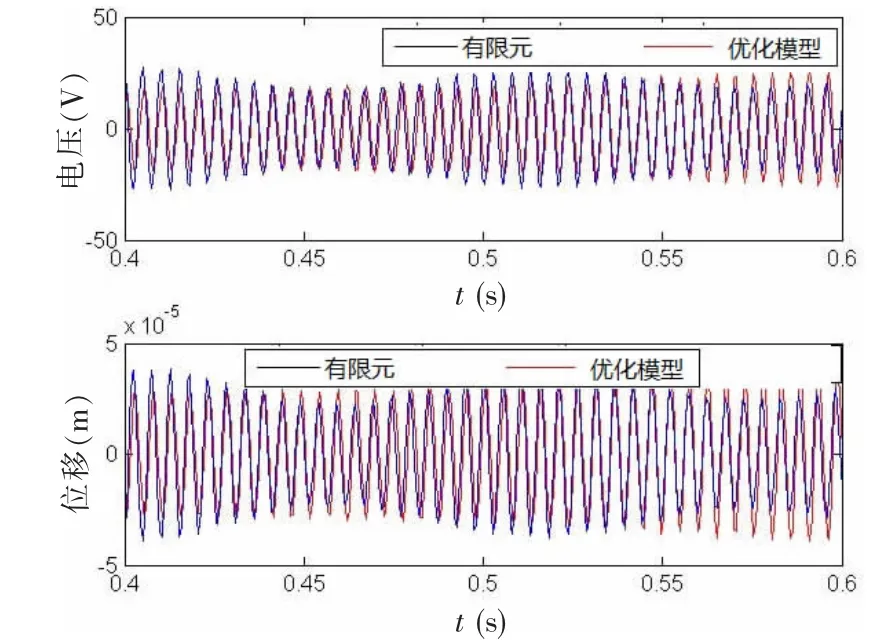
图13 水下压电圆柱壳有限元模型和优化模型电压、位移对比Fig.13 Voltage and displacement comparison between the finite element model and the optimal model for the piezoelectric cylindrical shell submerged in water

图14 水下压电圆柱壳有限元模型与优化模型扫频激励输出电压对比Fig.14 Voltage comparison in frequency domain between the finite element model and the optimal model for the piezoelectric cylindrical shell submerged in water

由以上结果可以确保水下压电圆柱壳体的优化模型是有效的，此模型可以作为作动器与传感器的位置优化模型。

3 传感器/作动器位置优化

控制系统中，一定数量的作动器、传感器能发挥最大效能的一个标准是使用最小的输入能量，测得最大的输出，达到最终的控制目的。依托第2 章所建立的水下压电智能圆柱壳体结构的优化模型，建立优化准则，对传感器/作动器位置进行优化。

则（2）式可变为

则

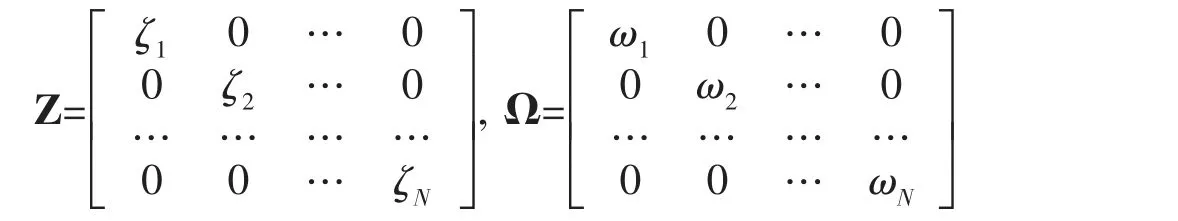
式中：ζi为结构的阻尼比，ωi为结构的固有角频率。

令

则（5）式可转换为模态坐标下的状态空间模型形式为

式中：B 矩阵为输入阵，C 矩阵为输出阵。

3.1 基于能量传递的传感器/作动器位置优化方法

3.1.1 作动器位置优化

若在同一传感测试位置下，输入能量的大小可考量作动器的作动功能的大小。基于状态方程描述的振动系统（7），输入能量用如下公式表示[6]：

式中Tf为终止时间。

又

其中

WcTf（）被称为可控Gram 矩阵，WcTf（）的范数越高，输入能量越小。对于稳定系统，当t→∞时，

其中

由此，最小化输入能量J 等同于Gram 矩阵Wc范数最大化。又Wc可由如下Lyapunov 方程求得：

由以上方程可以看出，可控性的大小不仅依赖于系统状态矩阵A，还依赖于输入矩阵B。其中，当振动系统确定之后，A 矩阵是不可变的。若想求得最大可控性矩阵，可通过变化输入矩阵B 来实现，而输入矩阵B 就决定了作动器的位置。由此，作动器的位置优化问题，等效于可控Gram 矩阵Wc范数最大化。

3.1.2 传感器位置优化传感器测试信号的能量可用下式表示[6]：

因此，传感器功能最大化意味着（14）式所表示的能量最大。类似于作动器的推导方法，可将其等效于可观Gram 矩阵的特征值配置最大化。可观Gram 矩阵表示为

Wo满足如下Lyapunov 方程

由以上方程可以看出，可观性的大小依赖于输出矩阵C，而输出矩阵C 可表示传感器位置信息。由此，传感器的位置优化问题，等效于可观Gram 矩阵Wo特征值最大化。

3.1.3 传感器/作动器位置优化准则

定义如下优化准则[6]

这个准则包含三项，第一项trace（）W，它与作动器传递给结构的总能量或传感器的输出能量成正比，即能够反映更适合结构和作动器/传感器进行能量交换的位置；）代表特征值的几何平均值；最后一项σ λi（）表示Gram 矩阵特征值的标准差，它惩罚那种同时具有很大和很小特征值的位置，也就是用可控性或可观性好的状态去掩盖可控性或可观性差的状态。当考虑安置作动器时，W=Wc，当用于安置传感器时，W=Wo。

3.2 位置优化结果

该圆柱壳的传感器数量为1，作动器数量为2，依托Abaqus-Matlab 联合建模平台建立的优化模型（7），优化这3 片压电片的位置，获取传感器与作动器的最佳粘贴位置。之后，通过同一激励下的响应大小验证结果的正确性，其中，外激励压电作动器的位置不做优化。

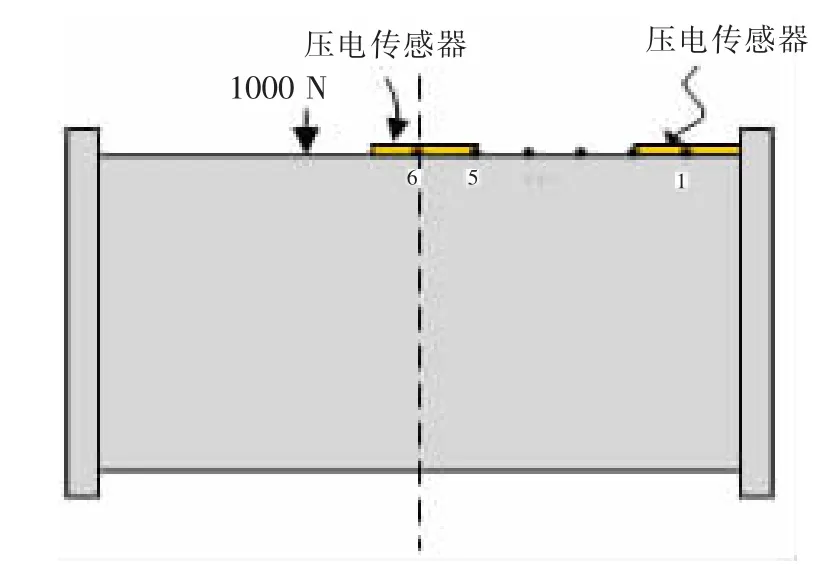
图15 压电传感器可选位置Fig.15 Optional locations of the piezoelectric sensor

图16 传感器不同位置的可观度Fig.16 Observability of the sensor in different optional locations

3.2.1 传感器的位置优化结果

由圆柱壳模型的对称性，沿圆柱壳长度方向，将传感器可选位置选定为图15 所示的位置。在图15 所示位置施加指向半径方向的1 000 N 的随机激励信号，由（17）式可计算不同位置处的可观性见图16。由此图可以看出，传感器的最佳位置为位置4。为了说明此位置确为最佳位置，关注该结构的前5 阶模态，评价传感器在100～600 Hz 处的电压输出的功率谱的大小，给出传感器输出电压的总功率谱密度如图17 所示，总功率谱密度的最大值也出现在位置4 处，由此说明位置4 确为能量输出的最大位置。

3.2.2 作动器位置优化结果

将传感器粘贴于最佳位置4 处，结合圆柱壳的对称性，将作动器的可能布放位置选定为图18 所示的位置，即沿长度方向布放11 个位置，沿圆周方向布放5 个位置（图18），计算55 个位置的可控度，关于长度及圆柱方向上的可控度结果见图19 所示。选定可控度最高的两个位置作为两个作动器的粘贴位置，由此可知，作动器的两个最佳位置一个位于长度方向为0.338 6 m，圆周方向为45°方向，另一个位移长度方向0.161 4 m，圆周方向135°。由此，传感器/作动器优化后的位置分布见图20 所示。

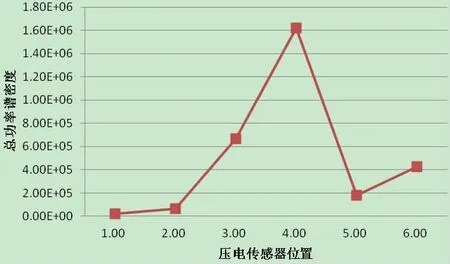
图17 传感器输出电压在100～600 Hz 处的总功率谱密度Fig.17 Total power spectral density of the output voltage from sensor in 100～600 Hz

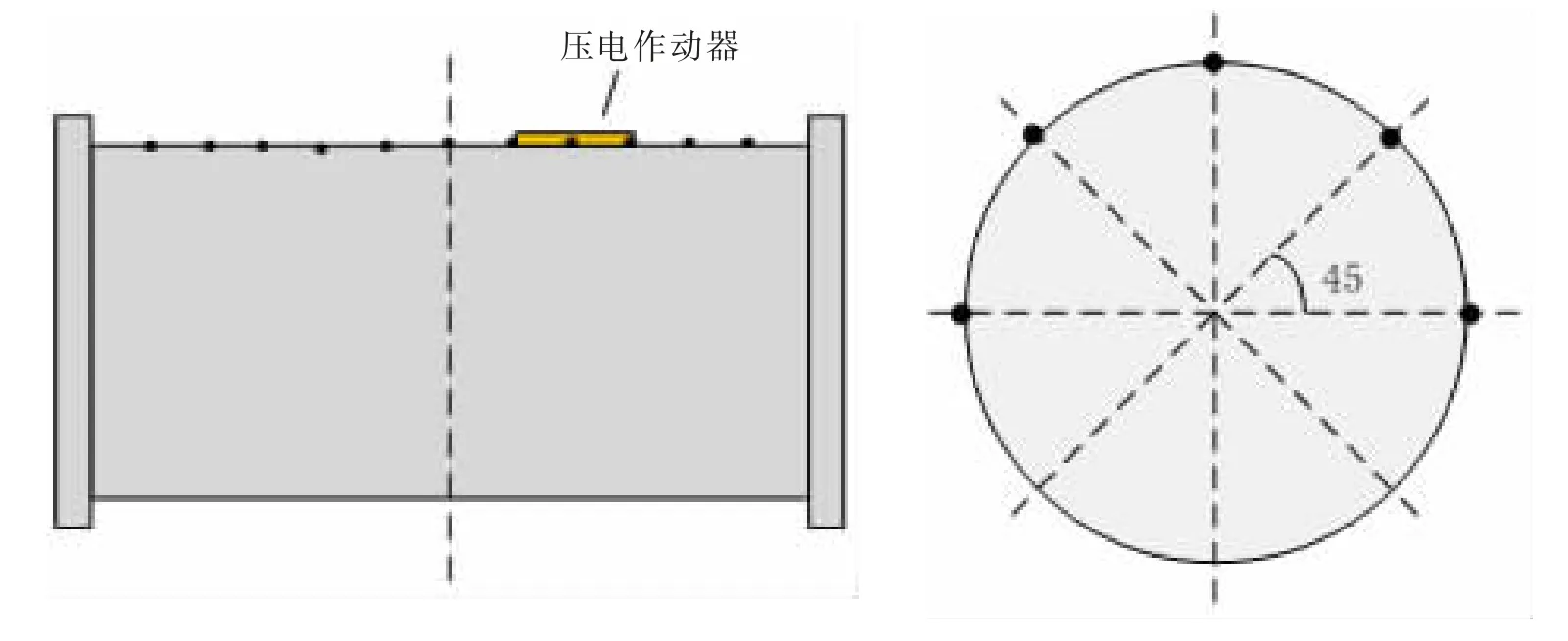
图18 作动器长度方向及圆周方向的可选位置Fig.18 Optional locations of the piezoelectric actuator at length direction and circumferential direction

图19 作动器在不同位置的可控度Fig.19 Controllability of the actuator in different optional locations

图21 未优化模型-1Fig.21 Unoptimal model-1

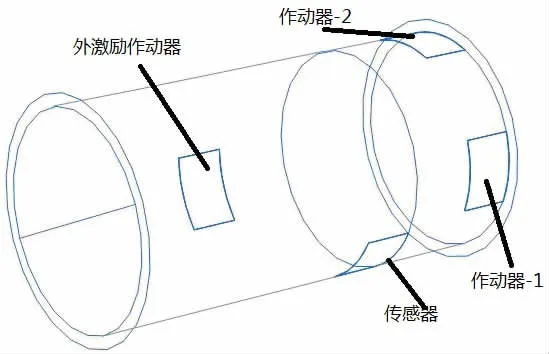
图22 未优化模型-2Fig.22 Unoptimal model-2

为了说明该位置的优越性，随意挑选了两个作动器与传感器不处在最优位置的模型（图21 与图22），给水下模型在两个作动器处施加相同的幅值为1 000 V 的Gauss 白噪声外激励电压，在压电传感器处输出电压响应见图23。由此图可以看出，三者时域响应的幅值差别明显，频率响应中未优化位置-2 的响应幅值明显小于其他两个位置。未优化位置-1 在第一个线谱处的幅值与优化位置的幅值差别不大，在其他线谱的幅值与优化位置处的幅值差别较大。总之，优化后的输出电压明显大于优化前的输出电压。由此可说明相同的外激励，优化后作动器、传感器能发挥最大效能。

4 结论

本文围绕压电智能圆柱壳体水下振动时传感器/作动器的位置优化问题，采用Abaqus-Matlab联合建模技术，获取压电—流体—结构三场耦合的优化模型，基于此模型，建立作动器传感器位置优化准则，得到了传感器作动器的最佳粘贴位置。由以上内容得出如下结论：

（1）采用Abaqus-Matlab 联合建模平台所建立的优化模型是有效的。基于流体-结构及压电-结构有限元理论，依托Abaqus-Matlab 联合建模平台，获得水下压电圆柱壳体优化模型。由阻尼、刚度、质量矩阵的结构形式及固有频率计算结果、正弦激励下的时域响应结果及扫频激励下的频率响应结果，验证了该建模方法的有效性。由此说明所建立的Abaqus-Matlab 联合建模平台，可解决流体—压电—结构三场耦合优化模型建立问题。

（2）依据基于能量传递的可控可观性传感器/作动器位置优化准则是正确的。基于Abaqus-Matlab 联合建模平台所获取的优化模型，考虑该模型的前5 阶模态，对频段为0～600 Hz 处的水下模型传感器及作动器的位置进行了优化，并通过传递到压电传感器的电压大小验证了该配置结果的合理性，由此可保证传感器、作动器在控制器实施过程中发挥最大效能。