联合载荷作用下撑杆结构极限强度研究

2019-05-14顾学康李生鹏李政杰汤明刚祁恩荣

船舶力学 2019年4期

赵南，顾学康，李生鹏，李政杰，汤明刚，祁恩荣

（中国船舶科学研究中心，江苏无锡214082）

0 引言

超大型浮体结构下浮体间依靠撑杆连接，撑杆起到支撑、传递变形和应力的作用。撑杆结构更类似于细长的杆件，结构强度最弱，在风、浪、流等海洋环境的作用下，撑杆结构受力复杂，失效模式较为复杂，在联合载荷的作用下更易产生极限承载能力不足的情况，极易发生破坏，进而影响平台整体结构的安全性。而目前国内外关于超大型浮体结构在复杂载荷作用下的结构极限强度模型试验开展较少，如Kaeding 和Fujikubo（2001）[1]根据有限元分析方法得出纵向压力作用下加筋板典型失效模式，基于ISUM 方法框架，发展新的ISUM 单元来模拟超大型浮式结构物的失效模式，该模型由大的板单元和梁柱单元组成。但是该方法中没有考虑焊接残余应力以及多个载荷的作用下超大型浮式结构物的失效模式等。Fujikubo（2005）[2]根据DNV（1994）[3]规范对超大型浮式结构物的底部结构以及甲板结构进行双轴压以及剪切下板格模型以及夹层板模型进行屈曲校核。张剑波[4]、姜峰[5]、杨鹏[6]等人先后开展过半潜平台结构极限强度研究，虽然超大型浮体为半潜式结构，但是由于超大型浮体总体结构尺度较大，因此其载荷等与半潜平台间仍然存在一定的差异。因此，有必要开展复杂载荷作用下的超大型浮体撑杆结构极限强度模型试验技术研究，为后续的数值仿真方法验证提供技术支撑。

本文主要以超大型浮体撑杆结构为研究对象，给出复杂载荷作用下模型设计的相似理论，试验模型设计方法，载荷加载方式等；完成复杂载荷作用下撑杆结构的极限强度模型试验，并对结构的极限强度试验数据进行分析，给出在复杂载荷作用下撑杆结构的失效模式以及极限承载能力；通过计及初始缺陷的数值仿真分析与试验结果的对比，验证数值仿真方法的正确性，并基于数值仿真方法，开展实尺度撑杆结构极限承载能力研究，给出联合载荷作用下撑杆结构极限承载能力曲线。

1 相似关系

对于压扭联合载荷作用下的撑杆极限强度试验，除了需要考虑压缩载荷作用下的塑性相似理论外，同样还需要考虑扭转惯性矩的相似，以保证在压扭联合载荷作用下的模型失效模式与原型相同以及极限载荷与原型相同。撑杆结构模型试验采用船用普通钢，主尺度缩尺比为λ，根据相似理论可以得出，力F 和扭转惯性矩J，弯曲惯性矩I 的相似关系如下式所示：

2 模型设计

2.1 模型设计

超大浮体单模块设置有8 个撑杆，尺寸相同，平均布置在两侧，撑杆位置如图1 所示[1]。撑杆总长30 m，为了增加撑杆与下浮体的连接区域，减小连接处的应力，两端逐渐增大截面尺寸，结构类似喇叭口，中间截面直径3 m。沿长度方向布置的横向隔板强弱交替，将撑杆分成若干段。撑杆结构模型材料采用船用普通钢，真实材料应力应变曲线见图2，其屈服强度为275 MPa，杨氏模量206 GPa，泊松比v=0.3。

综合考虑试验室加载能力及模型加工要求，选取缩尺比λ=5，试验区域对象总长度方向为6 m，宽度方向为1.0 m，高度方向为1.0 m，中间圆筒直径为0.6 m，见图3 所示。根据撑杆结构的受力和失效特征，选取压缩和扭转复杂载荷作用状态进行研究。压缩和扭转载荷联合作用采用一端固定，另一端施加压缩载荷，并在扭转载荷施加位置施加侧向力，以此研究压扭联合载荷作用下撑杆结构极限承载能力以及失效模式。根据模型设计的相似理论开展模型设计工作，等效前后的板厚及骨材如表1 所示，其中两端喇叭口位置处纵隔板扶强材按面积等效。

图1 撑杆布置图Fig.1 Arrangement plan of brace strut

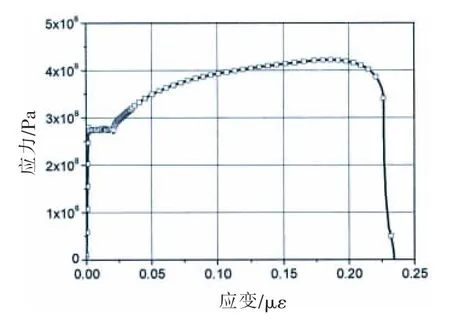
图2 应力—应变曲线Fig.2 Curve of stress-strain

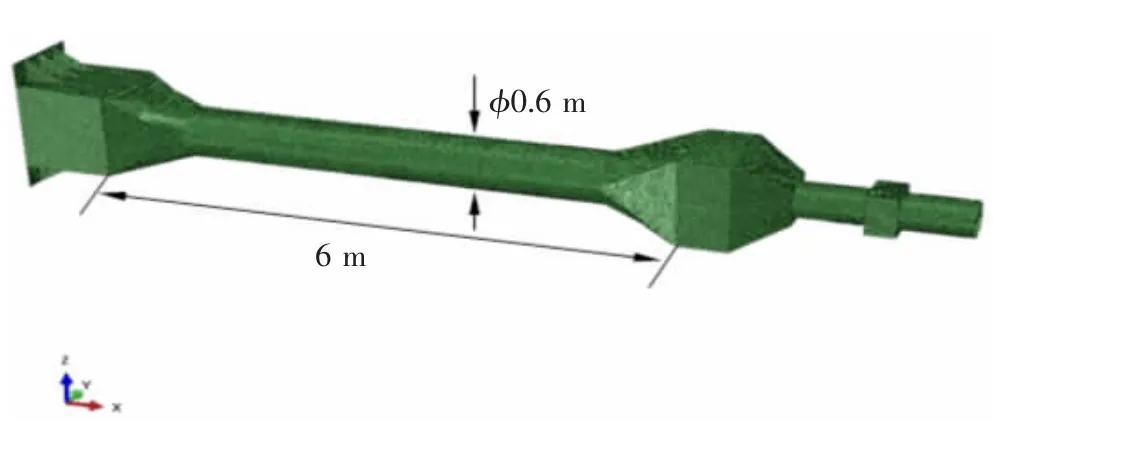
图3 撑杆结构主尺度Fig.3 Principal dimension of brace strut

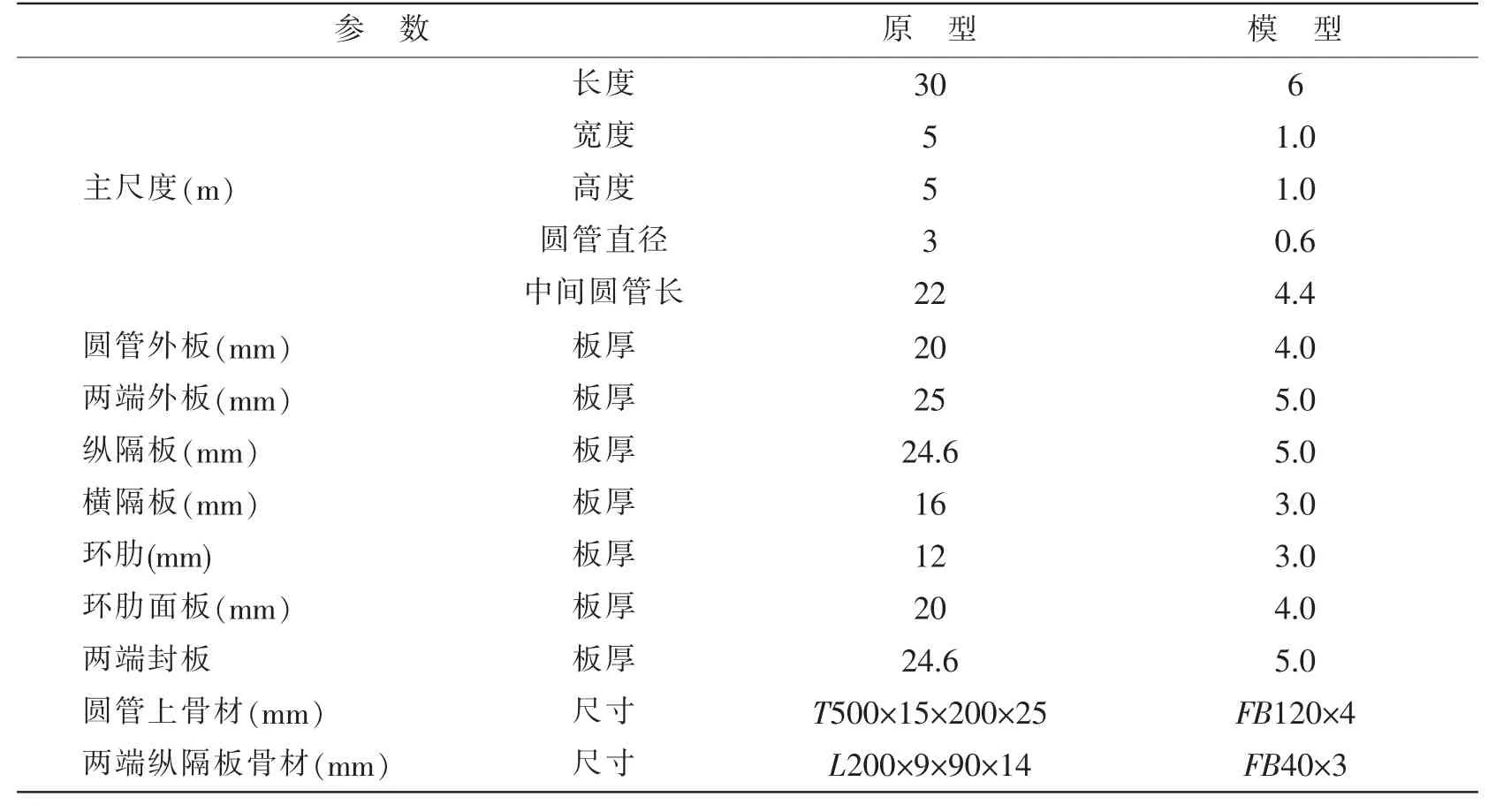
表1 撑杆原型与模型参数Tab.1 Parameter of brace strut prototype and model

试验段板厚分布图见图4～5 所示。其中横隔板共计9 个，中间的隔板为3 mm，两端的隔板为10 mm；两端喇叭口厚度为10 mm，其内部加强筋为FB40×3 mm。圆筒中间3.0 m 范围内板厚为4 mm，两端的外板厚度为10 mm；圆筒内部纵骨的板厚为4 mm。

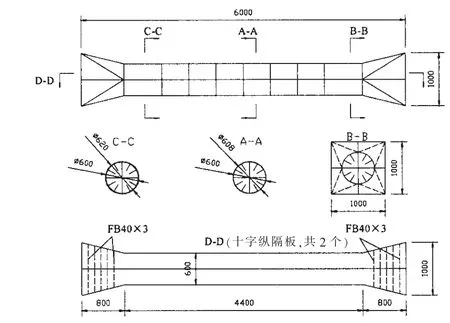
图4 圆管板厚分布 Fig.4 Plate thickness distribution diagram

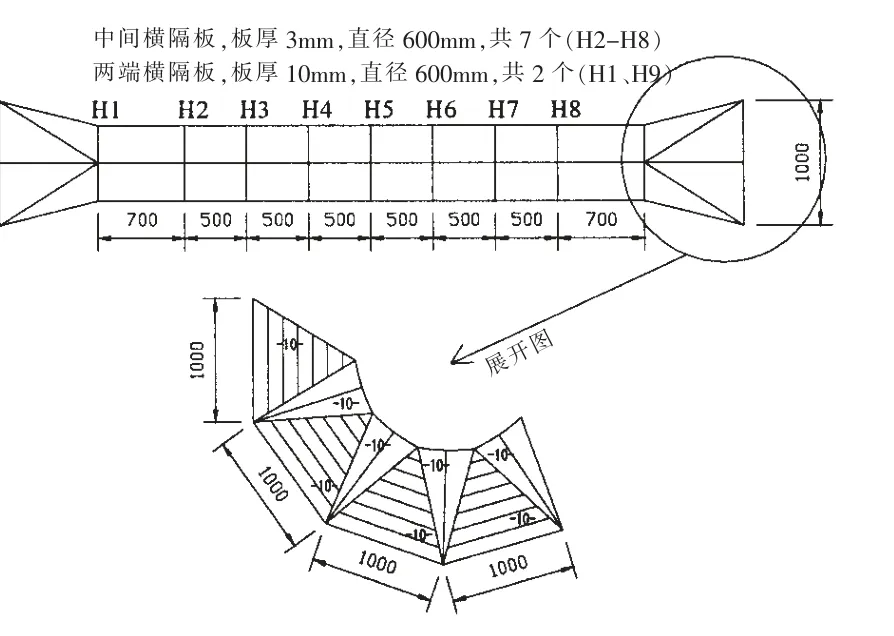
图5 两端外板展开图Fig.5 Outer plate expansion diagram

为验证本节对撑杆结构模型设计的合理性，根据表1 和图4～5 中的相关尺寸，建立撑杆结构原型和撑杆结构等效模型。在压缩和扭转载荷的作用下（扭转载荷为255 kN·m），选取撑杆一端为参考点，绘制压力—位移曲线，即横坐标为强制位移，纵坐标为支座对应方向的支反力，如图6 所示，极限状态的应力分布云图见图7 所示。通过图7 中的对比可以看出，等效前后的极限载荷、位移和等效前后的失效模式、失效位置等均接近，极限压缩载荷误差为2.66%。通过本节的计算结果可以看出，对于本节设计的等效撑杆极限强度试验模型是合理的。

2.2 模型加工

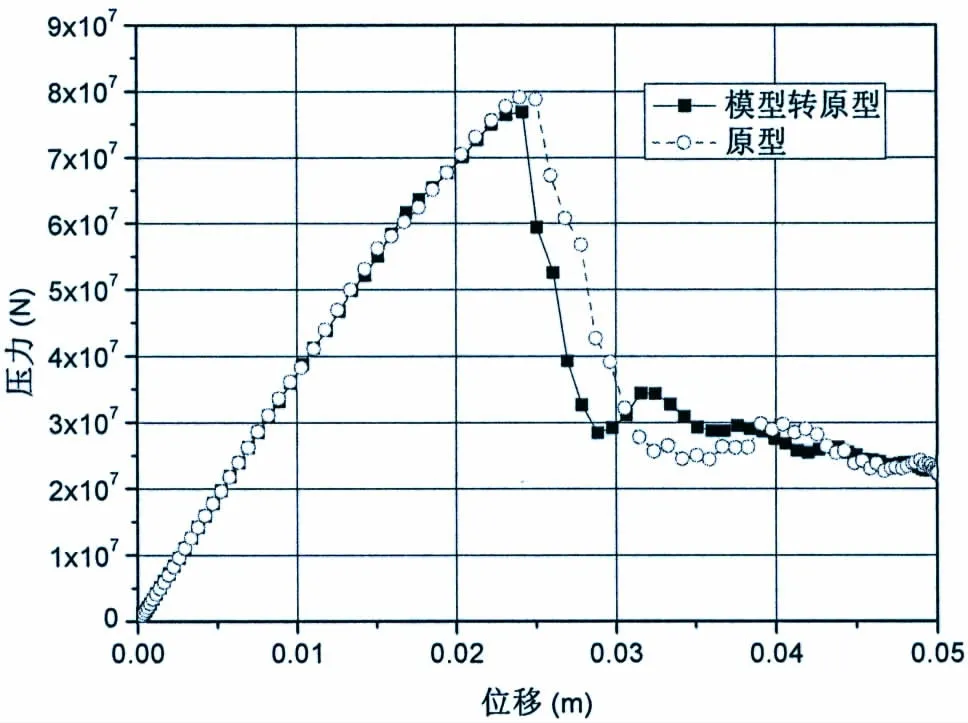
图6 联合载荷作用下压力—位移曲线Fig.6 Curve of force-displacement under combined loads

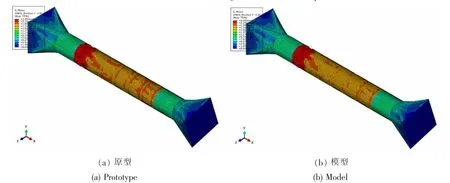
图7 联合载荷作用下极限状态应力云图Fig.7 Stress tensor for limit state under combined loads

图8 纵隔板焊接Fig.8 Welding of longitudinal clapboard

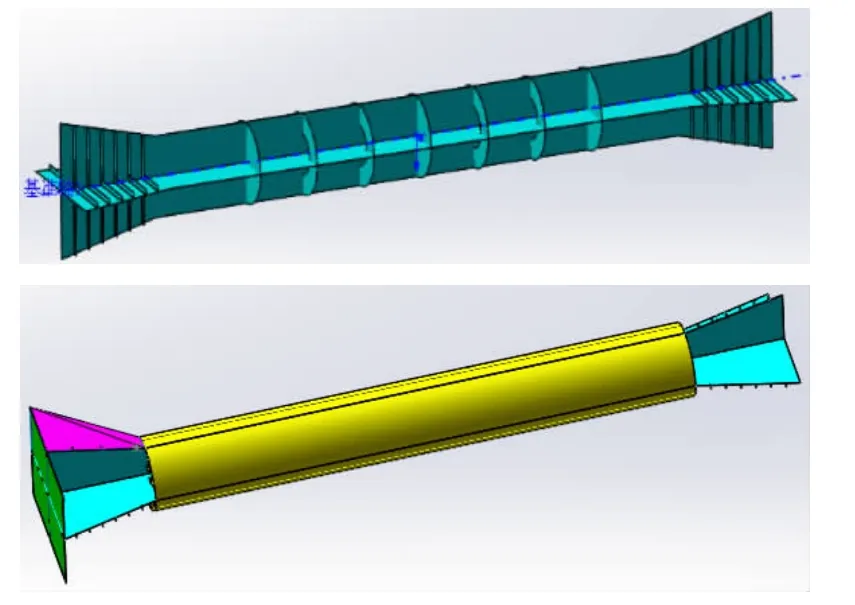
图9 其他结构焊接Fig.9 Welding for else structure

由于模型是包含2 个纵隔板、9 个横隔板、8 根纵骨以及圆筒外壳和两段喇叭口的结构，缩尺后模型圆筒直径仅为600 mm。模型的加工焊接难度较大，经过反复讨论制定了相应加工方案：1）先焊接两个纵隔板、端板成“十”字型布置，焊接时两端焊接工装固定，中间采用2～3 道十字工装固定，左右两边同时焊接，减少结构变形；2）在两个纵隔板之间焊接横隔板以及相应的纵向骨材，端部焊接骨材；3）最后将圆筒外壳进行卷板，分成12 份与上述结构进行焊接。

为了研究该方案是否合理可行，首先制作了一个长度为1.2 m 的撑杆局部模型，加工方案见图8～9所示。通过试加工模型发现，按照该方法进行撑杆局部模型的加工，其初始变形较小，圆度符合要求，加工完成后的局部模型见图10 所示。因此，本文中撑杆结构极限强度试验模型按照该方法进行加工，其中内部结构加工见图11 所示。

图10 撑杆局部模型焊接Fig.10 Welding of partial model for brace strut

图11 撑杆试验模型焊接Fig.11 Welding of trail model for brace strut

2.3 试验加载方式

对于压缩和扭转载荷联合作用的模型试验，在模型试验段最前端中心位置施加压缩载荷，在模型加载段的力臂上施加垂向载荷模拟扭转载荷，其中力臂长为1.5 m。在模型另外一端施加固支约束，将模型与试验室固定的三角支架相连接以保证其固支约束，加载方式见图12 所示。

图12 压扭载荷作用下撑杆模型试验加载方案Fig.12 Loading schemes of model test for brace strut under combined loads

2.4 测点布置

压缩和扭转载荷极限强度试验，在圆管各段处进行测点布置，其中测点S6、S9、S12、S15、S18、S21、S24、S27、S30、S33、S36 和S39为三向测点，沿纵向、轴向和45°剪切方向，其他测点为单向测点，单向测点沿纵向布置，测点均布置于跨中，共计56 个测点，其中三向测点12 个，单向测点44 个，分布见图13 所示。在压缩载荷加载端部（W1）以及扭转载荷施加位置（W2）附近布置位移传感器测量模型的轴向位移和扭转变形，在剖面B、C 处S15（W4）和S27（W3）测点附近各布置1 个位移测点，共计4 个位移测点和88 个应力通道。

2.5 模型初始状态描述

表2 中分别给出了撑杆结构压扭载荷作用下相关测点的初始变形及实际板厚描述。由于两个模型采用的均为同一批材料，因此其板厚测量结果基本一致，且由于按照统一的加工工艺进行加工，其初始变形控制得较好，最大变形为2 mm 左右，此处不做详细阐述。

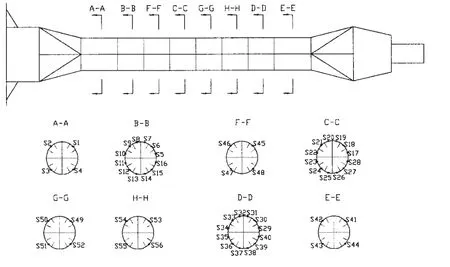
图13 撑杆模型试验测点布置图Fig.13 Arrangement plan of measuring points for model test of brace strut

2.6 试验测试内容

本次试验主要研究在压扭联合载荷作用下撑杆结构极限强度，因此试验测试主要内容为联合载荷作用下撑杆结构极限强度破坏试验，且为保证消除模型间隙及释放残余应力，需进行弹性范围内的加载试验，相应的极限强度试验载荷加载次序见表3。

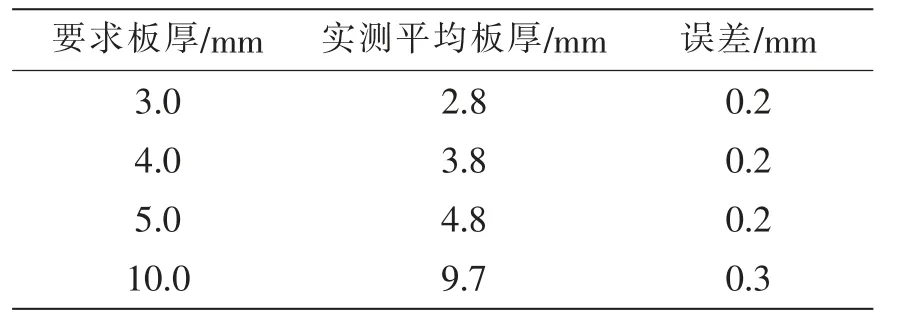
表2 撑杆结构初始板厚描述Tab.2 Description of initial plate thickness of brace strut

表3 联合载荷作用下撑杆结构极限强度试验工况Tab.3 Ultimate strength load case for brace strut under combined loads

3 联合载荷作用下撑杆极限强度试验数据分析

图14 中给出了压扭载荷作用下撑杆结构部分测点应变随载荷变化曲线，通过载荷—应变曲线可以发现，失效剖面B 大部分测点已经达到极限应变（1 300 με 左右），其余剖面大部分测点已经超过了屈服应变（1 335 με 左右）。且当载荷达到2 000 kN 左右，部分测点已经达到屈服应变，开始进入塑性阶段，但仍然可以承受载荷，如S26 部分测点在载荷为2 400 kN 前处于弹性状态，但当载荷继续增大后，其应变反而减小，可见随着载荷的增大，存在应力重新分布的情况。

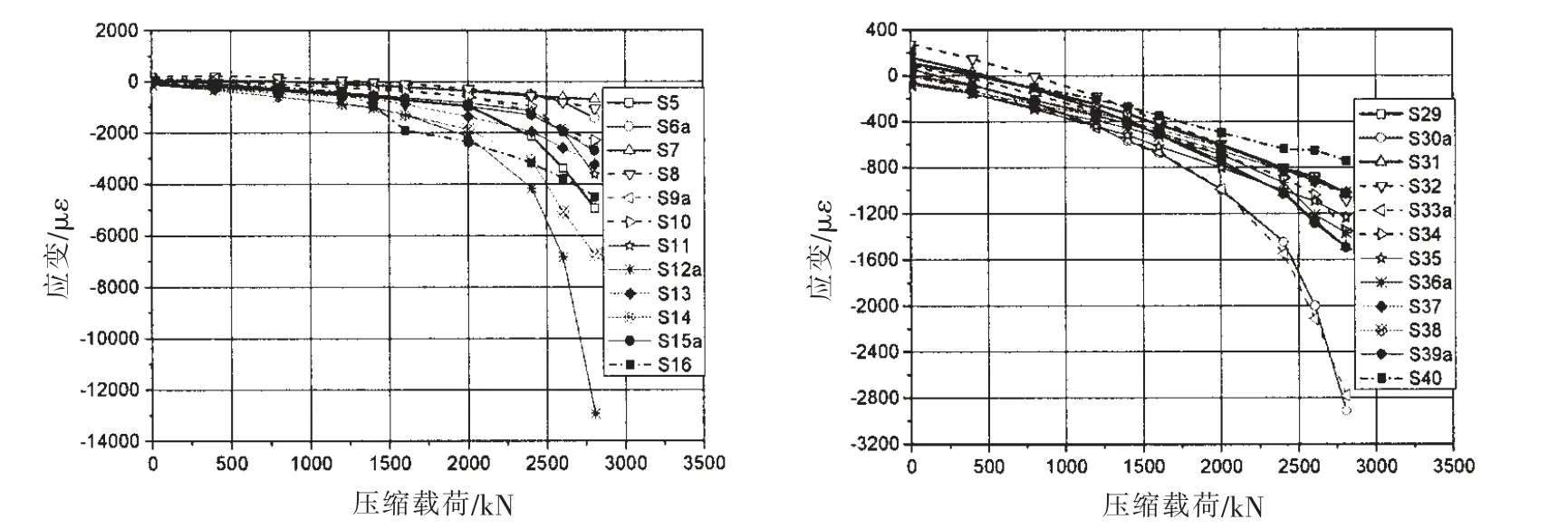
图14 联合载荷作用下部分测点应变—载荷变化曲线Fig.14 Strain-load curve of partial measuring points under combined loads

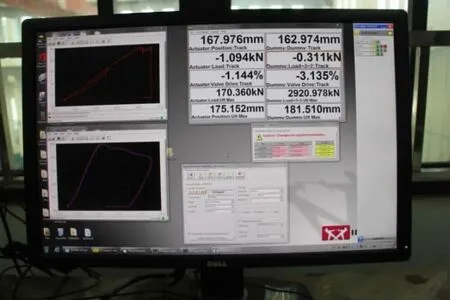
图15 压扭载荷作用下极限压缩载荷值Fig.15 Ultimate load under compressive and torsion

图16 压扭复杂载荷作用下失效模式Fig.16 Failure mode under compressive and torsion

当载荷达到2 800 kN 后，继续施加载荷，当载荷达到2 920 kN 后，模型完全形成塑性铰，载荷突然下降导致该极限载荷未能及时采集到。因此，图14 中的应变-载荷曲线未给出极限状态的应变值。但通过图15 的压缩载荷曲线以及最大值可以发现，压缩载荷最大值达到了2 920 kN，之后载荷突然下降。图16 为模型在载荷达到2 920 kN 后模型的失效模式，为典型的压扭联合作用下产生沿着斜向45°方向变化的屈曲失效模式。

4 试验与仿真结果对比分析

根据试验模型以及加载过渡段的相关尺寸，进行有限元模型的建立，过渡段及模型工装等结构材料为Q345B，试验段材料为船用普通钢，真实材料的屈服极限为275 MPa，相应的材料曲线见图2 所示。模型中板厚采用试验模型真实板厚，并计及初始变形及焊接残余应力影响，见图17～18 所示。相应的边界条件见图19 所示。

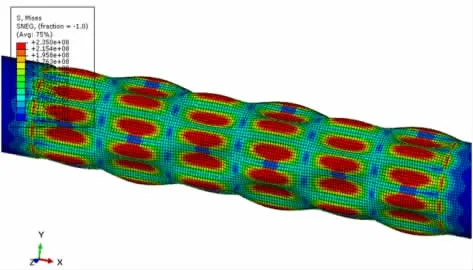
图17 初始变形Fig.17 Initial deformation

图18 焊接残余应力Fig.18 Welding residual strength

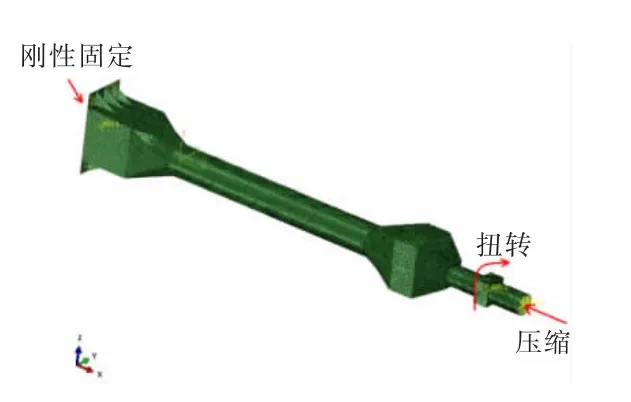
图19 边界条件及载荷施加Fig.19 Boundary conditions and loading

为了保证与模型试验载荷施加方式相同，对于压扭联合载荷作用下的撑杆结构数值仿真模型，将纵向载荷与扭转载荷分开施加，即首先施加扭转载荷，大小为255 kN·m 的扭矩，待其稳定后在此基础上施加纵向节点位移，以便消除载荷施加方式对数值仿真计算结果的影响。

图20 中给出了撑杆结构压扭载荷联合作用下极限状态应力分布情况，图21 中给出了撑杆结构极限状态失效模式的数值仿真结果和试验结果对比，通过对比可以发现数值仿真中得到的失效模式与试验得到的结构失效模式相同，均为压扭联合作用下的典型斜条纹失效模式；通过图22 中的载荷-位移曲线可以得出，数值仿真方法计算的压缩极限载荷为3.03 MN，与试验结果2.92 MN 的相对误差为3.76%。

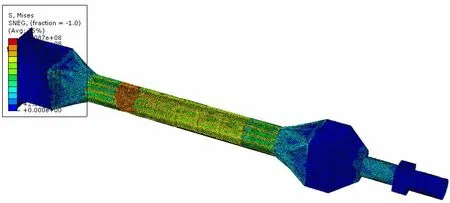
图20 联合载荷作用下极限状态应力分布云图Fig.20 Stress tensor for limit state under combined loads

图21 压扭复杂载荷作用下撑杆结构极限状态失效模式对比Fig.21 Comparison of failure modes between model test and numerical simulation under combined loads

5 实尺度撑杆结构压扭载荷作用下极限承载能力

本节中所采用的模型为实际超大型浮体撑杆结构，撑杆结构相对简单，主要包括纵骨、弱横隔板、强横隔板、相应的纵隔板以及圆柱外壳和两段的喇叭口等结构，相应的有限元模型以及去除外壳和纵隔板的内部结构见图23 所示，板厚及主尺度采用表1 中原型参数，初始变形取为5 mm，并采用预应力的方式计及焊接残余应力的影响。模型板格间划分8 个网格，纵骨划分6 个网格，面板划分2 个网格。总体的网格数量为10 万左右，其中四边形单元采用S4R5，三角形采用STRI3 单元模拟。相应的边界条件为左端施加固支约束，右端剖面施加扭矩和轴向压缩位移载荷。材料模型采用屈服极限为315 MPa 的理想弹塑性模型。

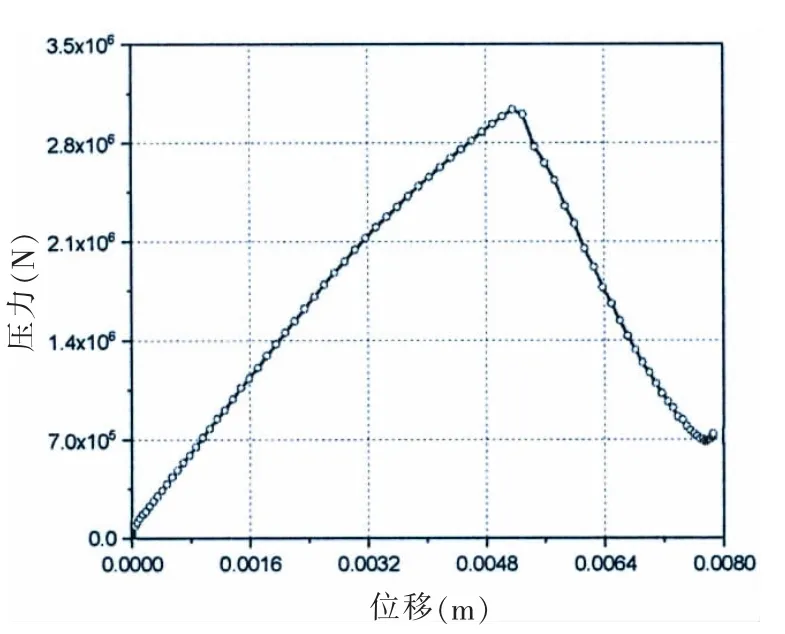
图22 联合载荷作用下撑杆结构载荷—位移曲线Fig.22 Load-displacement curve of brace strut under combined loads

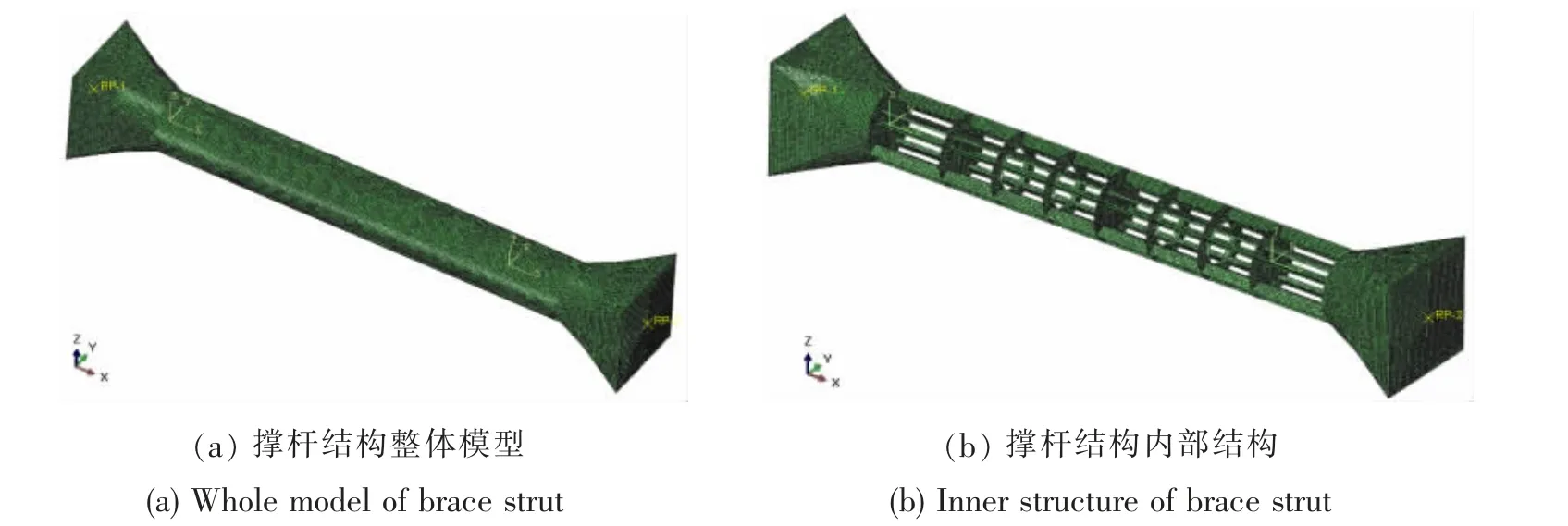
图23 撑杆结构数值仿真模型Fig.23 Numerical simulation model of brace strut

图24 中给出了不同扭转载荷作用下的结构压缩载荷—位移曲线。通过曲线可以发现，当扭转载荷较小时，对结构的极限承载能力影响较小，失效模式主要体现在受压失稳；通过图24 中不同扭转载荷作用下的失效模式可以看出，当扭转载荷较大时，对结构的极限承载能力影响较大，失效模式由传统的受压失稳向压缩和扭转共同作用下导致的斜波纹形状的失稳；而当扭转载荷单独作用时，失效模式又转变为明显的塑性流动。

图24 不同扭矩作用下撑杆结构载荷—位移曲线及承载能力曲线Fig.24 Load-displacement curve and interaction curve of brace strut under different torsion

根据图24 中数值仿真计算结果，通过曲线拟合的方式，得到如（2）式中的压扭载荷作用下结构极限承载能力曲线。通过图中拟合曲线与数值仿真结果的对比可以发现，按照（2）式拟合得出的各扭矩载荷计算点处的压缩极限承载能力与数值仿真结果较为接近，仅在扭转载荷为48 MN·m 和49 MN·m处偏差稍大，分别达到了4%和5.8%，其他计算点均小于该误差。因此，本文给出的拟合公式可用于工程上的撑杆结构极限强度设计中。