超大型海上浮式结构物连接器基座强度分析

李良碧，李嘉宾，董佳欢，贾倩倩，顾海英，汤明刚，罗广恩

（1.江苏科技大学 船舶与海洋工程学院，江苏 镇江212003；2.中国船舶科学研究中心，江苏 无锡，214082）

0 引 言

超大型海上浮式结构物[1-2]体积庞大，结构复杂，相比于陆地结构，它长期服役在岛、礁和浅滩附近，海洋环境十分复杂。在服役过程中不仅要承受风、浪和流等载荷，还要面临偶然性的灾害和载荷，这些都会对超大浮体的各个单模块之间产生碰撞和挤压，对超大浮体连接器产生极大的破坏力，降低了平台的承载能力，从而影响超大浮体的安全使用。因此对超大浮体连接器基座的强度分析是其成功设计的关键。

目前国内外关于海上浮式结构物连接器的研究主要集中在连接器的载荷上[3-7]。Derstine 等[8]通过对比柔性连接器与刚性连接器在不同模块结构和不同海况下所能承受的载荷，得出通用的柔性连接器比传统刚性连接器的载荷显著减小的结论。管义锋等[9]估算了船舶碰撞引起的连接器载荷的数量级，并对比波浪引起的连接器载荷，得出了两者属于同一数量级的结论。于澜等[10]研究了超大浮体多模块之间的相互作用对连接器载荷的影响。研究表明，超大型海上浮式结构物模块间的相互作用对刚度不同的连接器载荷的影响不同，当浪向角较小尤其是迎浪时，影响十分明显；当浪向角较大尤其是横浪时，模块间的相互作用对连接器载荷的影响可以忽略不计。

综上所述，国内外对连接器基座强度的研究较少。因此，本文开展了对超大型海上浮式结构物连接器基座静强度及极限强度的计算和分析。研究结果可为超大浮体连接器基座的设计和安全可靠性分析提供相关理论依据。

1 理论基础

1.1 有限元分析中的非线性问题

在结构有限元分析中，存在三种非线性因素[12]，分别是材料非线性、几何非线性和边界非线性。船舶与海洋结构强度分析中主要涉及材料非线性和几何非线性。

1.1.1 材料非线性

金属弹塑性材料在弹性范围内，应力—应变的变化规律是线性的，此时材料的响应是可逆的；若应力超过材料的屈服强度，外载荷消失时，材料不能完全回复到初始状态，材料具有不可逆性，如图1 所示。

1.1.2 几何非线性

在结构分析过程中，结构在外力作用下发生几何大变形引起结构响应的非线性，称为结构的几何非线性。杆件的屈曲失稳现象是常见的几何非线性问题。

1.1.3 边界非线性

在结构分析过程中，由于结构边界条件发生变化而引起的响应非线性，称为边界非线性。碰撞和接触是最常见的边界非线性问题。

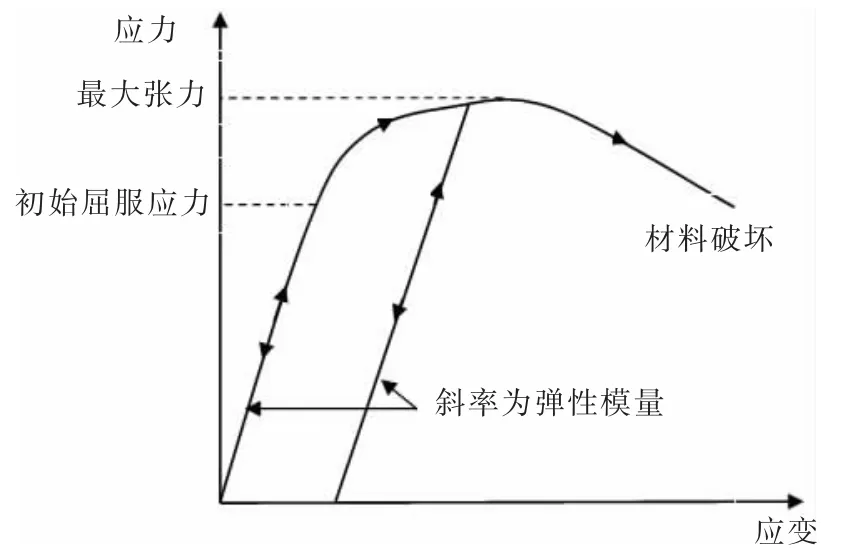
图1 弹塑性材料应力—应变曲线Fig.1 Stress-strain curve of the elastic-plastic material

1.2 非线性有限元分析方法

非线性有限元分析方法是可以考虑材料非线性、几何非线性和边界非线性的有限元分析，被越来越多地应用到工程计算中，逐渐成为计算和评估结构极限强度最理想的方法。非线性有限元法分析流程如图2 所示。

非线性有限元强度计算中最常用和最有效的方法是弧长法和准静态法。本文采用准静态法计算连接器基座的极限强度。

准静态分析法用载荷的缓慢加载来模拟静态，实质上是一个结构动态求解的过程。结构非线性运动方程的显示求解法采用中心差分法对运动方程（1）进行显示的时间积分，载荷步的动力学条件由上一个增量步的动力学条件决定，直到求解时间结束。

图2 非线性有限元分析流程图Fig.2 Flow chart of nonlinear finite element analysis

式中：［M ］为质量矩阵；｛a ｝为加速度列阵；｛P ｝为载荷列阵；｛I ｝为内力列阵。

采用中心差分法的显示求解方法不存在收敛问题，且当模型比较大时，需要的系统资源比较少。

使用准静态分析法时，需要注意加载速度的设置，加载速度过快会出现载荷-位移曲线震荡的现象，导致求解结果产生较大的局部偏差，无法达到“准静态”的要求。如果加载速度过慢，则需要耗费大量的时间。在分析时，一般选取多个加载速度进行比较分析后选取合适的加载速度。

2 连接器基座静强度分析

2.1 连接器基座概况

超大浮体单模块由上箱体、立柱、横撑和下浮体等结构组成，如图3 所示。下浮体横向设置，连接器基座位于上箱体内，如图4 所示。

含连接器的超大浮体示意图如图5 所示，其中M1～M3 表示单模块，C1～C4 表示连接器。相邻两个模块之间的连接器沿超大浮体中纵剖面对称布置，基本模块的数量因需而定。

本文所研究的超大浮体（图3）基本模块的上箱体长300 m，宽100 m，高6 m。上箱体共四层甲板，从上至下依次是主甲板、支撑甲板、机械甲板和底甲板，每两层甲板之间的间距为2 m，最下层甲板与立柱相连。连接器基座位于上箱体内，除了共用上箱体的四层甲板之外，还在主甲板和支撑甲板之间增设连接器基座主甲板，在机械甲板和底甲板之间增设连接器基座底甲板，因此连接器基座从上到下共包含六层甲板。为了对连接器结构进行加强，在基座内设置纵横舱壁，主体形状为梯形，同时对紧邻梯形部位的上箱体骨材进行了加密，如图6 所示。

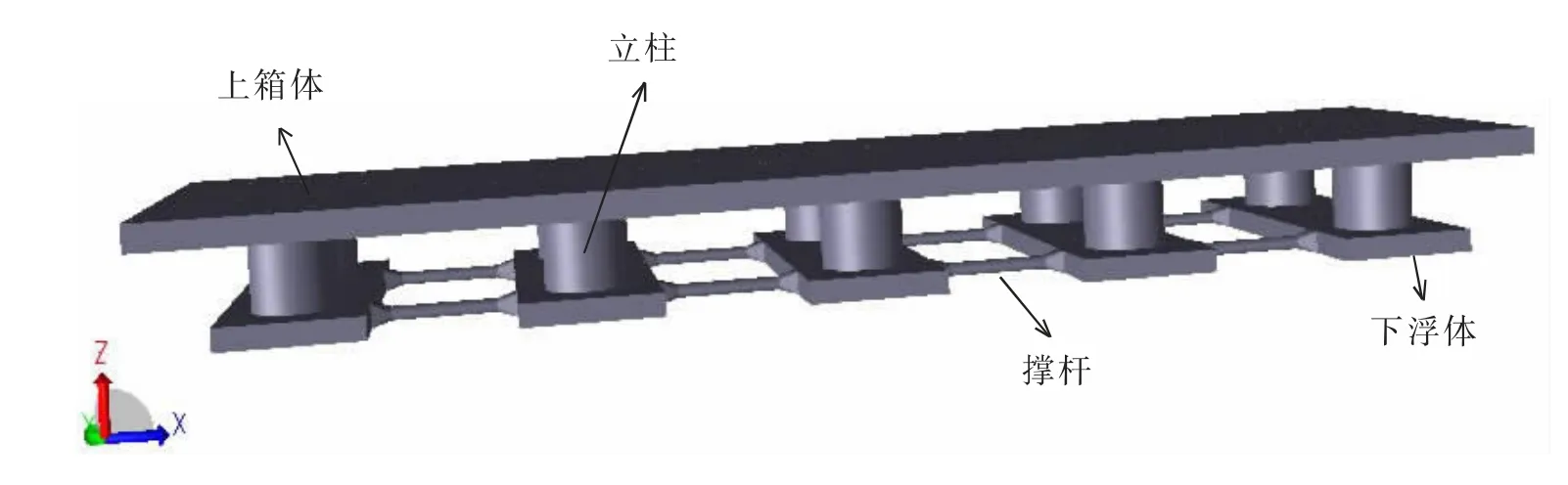
图3 超大浮体单模块示意图Fig.3 Sketch map of single module of VLFS

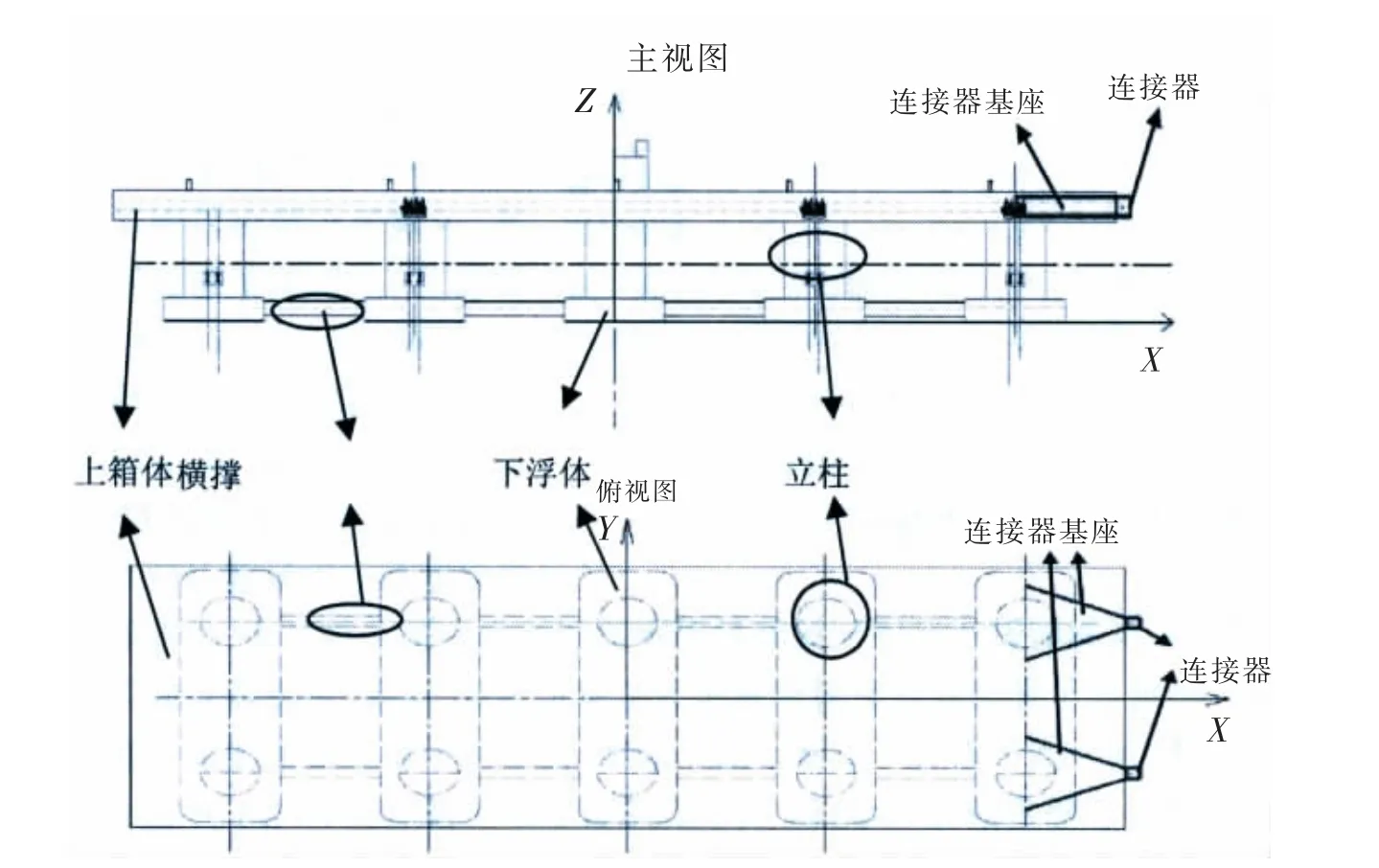
图4 超大浮体单模块右侧连接器基座位置示意图Fig.4 Sketch map of position of the right connector base of single module of VLFS

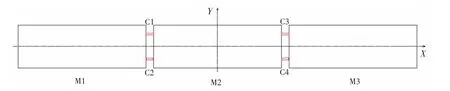
图5 含连接器的超大浮体示意图Fig.5 Sketch map of VLFS containing connectors

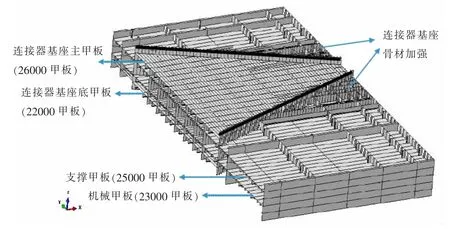
图6 连接器基座结构图Fig.6 Structure of connector base

2.2 连接器基座有限元模型

采用Patran 有限元软件建立含连接器基座的上箱体局部结构有限元模型。上箱体甲板骨材间距1 m，连接器基座的骨材相对较密。网格尺寸为1 m×1 m，局部需要加强部位的网格尺寸细化为0.5 m×0.5 m。为了避免边界条件的设置对基座结构强度分析的影响，本文采用两种有限元模型。

2.2.1 模型一

以超大浮体单模块为研究对象，选取含有单个连接器基座的上箱体局部结构，尺寸为45 m×50 m。通过计算分析，当立柱高度取4 m 时可以消除边界条件的影响，如图7 所示，有限元模型如图8 所示。

图7 模型一示意图Fig.7 Sketch map of model 1

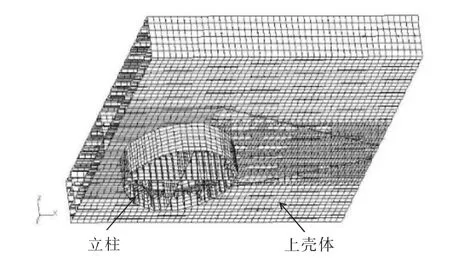
图8 模型一有限元模型Fig.8 Finite element model of model 1

2.2.2 模型二

选取含左、右舷两个连接器基座的上箱体局部结构，尺寸为90 m×100 m，通过计算分析，当立柱取4 m 时可以忽略边界条件的影响，如图9 所示，有限元模型如图10 所示。

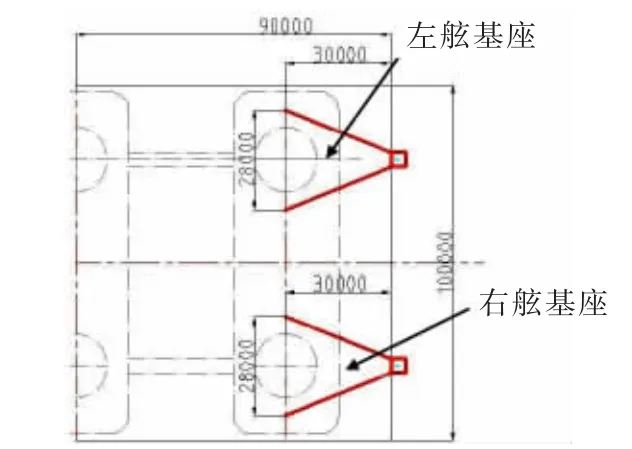
图9 模型二示意图Fig.9 Sketch map of model 2

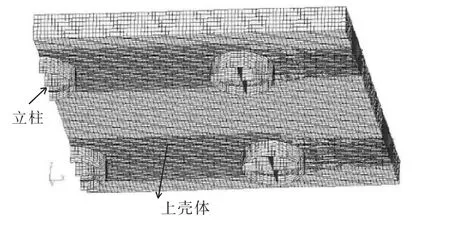
图10 模型二有限元模型Fig.10 Finite element model of model 2

2.3 边界条件设置

模型一和模型二的立柱底端和远离连接器基座的上箱体一端采用刚性固定；同时模型一在相对超大浮体单模块结构的中纵剖面上施加对称约束。

2.4 载荷和工况

根据相关超大浮体研究资料[13]，连接器基座载荷如表1 所示，载荷坐标系如图4 所示。为了方便施加载荷，采用有限元分析中MPC 点（参考点）设置载荷的施加[14]，即将受力部位关联到与甲板围壁板外部相距0.2 m 的MPC 点上，耦合它们之间的六个自由度，在MPC 点上施加相关载荷，如图11 所示。

表1 连接器基座载荷Tab.1 Loadings of the connector base

图11 设置MPC 点（参考点）Fig.11 Setting MPC point(reference point)

受各个模块相互运动的影响，连接器会受到来自各个方向的载荷，现将连接器基座受到的三个方向的载荷进行组合来分析整体应力和变形情况，从而确定危险的工况，不同方向载荷组合工况如表2 所示。

表2 不同方向载荷组合工况Tab.2 Combination condition with different direction loadings

续表2

2.5 连接器基座静强度有限元分析结果

两种模型中均采用4 m 高的立柱，施加约束和载荷，进行强度计算。

模型一在工况A-1（表2）下整体Von mises 应力如图12 所示，整体变形如图13 所示。由图12 可知，在基座单独受到X 方向100 MN 的拉力时，基座结构整体Von mises 应力不大。由图13 可知，模型一在受到X 方向100 MN 的拉力的作用下，连接器有向下偏移的趋势，最大偏移量为6.87 mm。基座与连接器连接部位应力最大，出现在围壁的水平扶强材处，为319 MPa，如图14 所示。立柱与上箱体底甲板连接部位应力不大，此处应力最大值出现在立柱纵舱壁与上箱体底甲板连接处，为50.5 MPa，如图15 所示。各工况下的高应力位置以及最高应力值如表3 所示，最大变形情况如表4 所示。

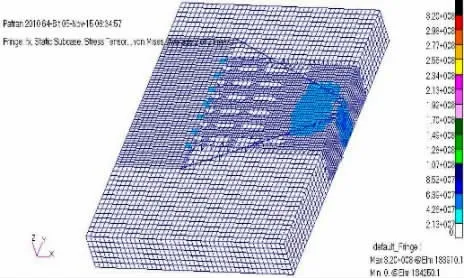
图12 A-1 工况下基座整体应力Fig.12 Global stress of connector base under A-1 condition

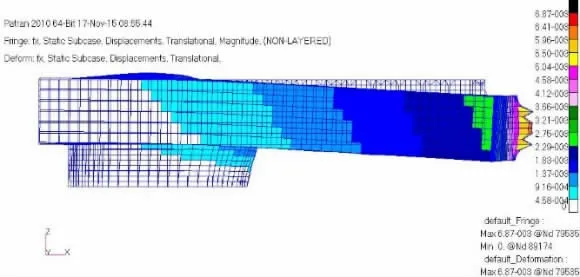
图13 A-1 工况下基座整体结构变形Fig.13 Global deformation of connector base under A-1 condition

图14 基座与连接器连接部位应力Fig.14 Stress of joint of base and connector

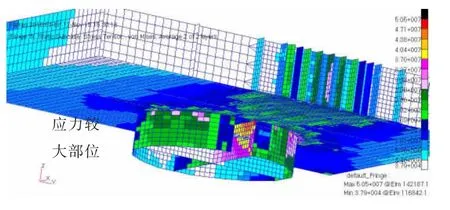
图15 立柱与上箱体连接处应力Fig.15 Stress of joint of column and upper box

表3 模型一和模型二在A-1～A-9 工况下高应力区域最大Von mises 应力（MPa）Tab.3 Maximum Von mises stress of model 1 and model 2 under different condition(MPa)

续表3

表4 模型一和模型二不同工况下的最大变形量和变形趋势Tab.4 Maximum deformation and deforming dependency of model 1 and model 2 under different condition

从表3 可以看出两种模型：

（1）在各工况下（表2）总体结构应力不大，但存在两处高应力区，即基座与连接器连接处以及立柱与上箱体底甲板连接处；（2）X 方向的力对基座与连接器连接部位应力影响较大，Z 方向的力对立柱与上箱体底甲板连接处应力影响较大，Y 方向的力对应力影响较小，Y 方向的力对基座与连接器连接部位应力的影响要比立柱与上箱体底甲板连接部位应力的影响大一些；（3）当X、Y、Z 三个方向同时受力时，结构应力最大。

从表4 可以看出两种模型Z 方向向上的载荷对模型的整体变形影响最大，Y 方向上的载荷对模型整体变形影响不大，几乎可以忽略。

图16 和图17 为模型一和模型二在各工况下高应力部位最大Von mises 应力比较。

由表3、图16 和图17 可知：

（1）虽然两种模型对基座与连接器连接部位的最大Von mises 应力没有明显变化，但是对于立柱与上箱体底甲板连接处的最大Von mises 应力有明显变化，模型二要比模型一高，最高超出模型一45%左右。这可能是由于两种模型的宽度相差较大，导致边界约束的效果不同而引起的计算结果的差别。因此在分析连接器基座强度问题时，应该注意模型尺寸的选取。

图16 不同模型基座与连接器连接处Von mises 应力比较Fig.16 Von mises stress of joints of base and connector of different models

图17 不同模型下立柱与上箱体连接处Von mises 应力比较Fig.17 Von mises stress of joints of column and upper box of different models

（2）由于模型二比模型一尺寸大，柔度大，所以变形相对较大。

3 连接器基座极限强度分析

3.1 连接器基座极限强度分析流程

考虑到几何非线性和材料非线性,对连接器基座施加强迫位移，采用非线性有限元准静态法[12]，通过参考点的位移与支座支反力的载荷-位移曲线，得到不同方向受力下的极限承载力。采用Abaqus 有限元分析软件的显示求解器，进行连接器基座极限承载力分析。

3.2 材料特性

连接器基座的材料为AH32，分析时设为理想弹塑性材料，其材料特性如表5 所示。

3.3 有限元模型和边界条件

有限元模型和边界条件见2.2～2.3 节。

3.4 载荷加载曲线

采用准静态法计算连接器基座的极限承载力时，施加的载荷要求尽可能光滑，突然和急促的运动会产生应力波，导致计算结果的准确性降低[15]。在Abaqus 中设置一条光滑的载荷加载曲线，以保证加载方式光滑，如图18 所示。

3.5 连接器基座极限承载力有限元分析

对超大型浮式结构物连接器基座在X 方向受压、X 方向受拉和Z 方向向上受拉分别进行加载，计算连接器基座在这三个方向的极限承载力。

3.5.1 X 方向受压

在模型一参考点（图11）施加随时间光滑变化的X 方向强迫位移d，使连接器基座在X 方向受压，通过计算，得到参考点载荷-位移的关系，如图19（a）所示。根据两倍弹性斜率法分析得到了连接器基座的极限承载力为728.3 MN，此时参考点的位移为53.5 mm，极限受压状态下含连接器基座的上箱体局部结构的整体Von mises 应力如图19（b）所示。

表5 连接器基座材料特性Tab.5 Material properties of connector base

图18 加载幅值曲线Fig.18 Loading amplitude

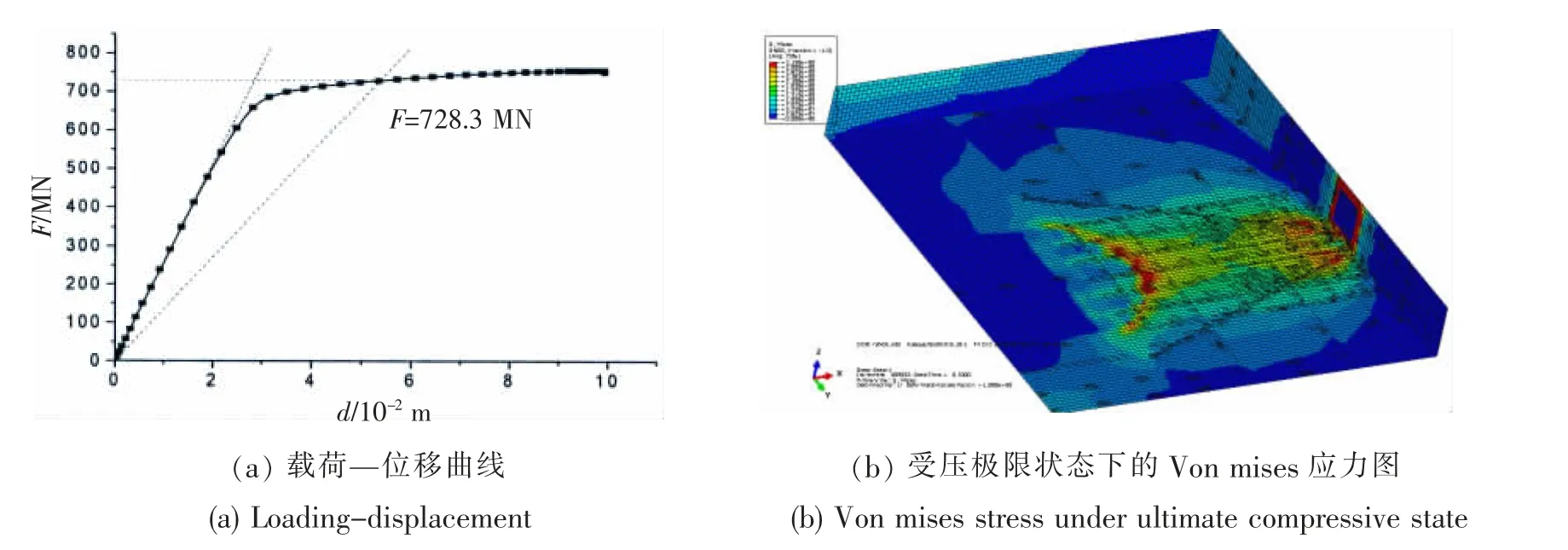
图19 X 方向受压的计算结果Fig.19 Results under compression loading from X direction

由图19 可知，连接器基座在X 方向的极限受压承载力为728.3 MN，远大于载荷预报值100 MN。基座与连接器连接部位，即载荷施加部位应力较大，应会先达到屈服破坏。与静强度分析结果一致，除了在基座与连接器连接处，还存在一处高应力区，即立柱与上箱体底甲板连接处，其应力小于基座与连接器连接处。

模型二的连接器基座左舷和右舷参考点的载荷-位移曲线，如图20 所示。采用和模型一相同的分析方法，得到左舷连接器基座极限受压承载力为731.1 MN，右舷连接器基座极限受压承载力为721.1 MN，两个参考点到达极限受压状态时的位移均达到60.8 mm。基座与连接器连接部位应力较大，应会先达到屈服破坏，如图21 所示。

图20 载荷—位移曲线图Fig.20 Loading-displacement

3.5.2 X 方向受拉

在模型一参考点上施加强迫位移d，使连接器基座在X 方向受拉，参考点载荷-位移曲线如图22所示，连接器基座的极限受拉承载力为704.8 MN，此时参考点的位移为53.5 mm。连接器基座在X 方向的极限受拉承载力为704.8 MN，远大于100 MN 的预报值。在计算过程中，随着参考点处强迫位移的增加，首先达到屈服极限的是基座与连接器连接处。除了基座与连接器连接处，立柱与上箱体底甲板位置也出现了应力集中，相比基座与连接器连接处应力较小。

模型二参考点的载荷—位移曲线如图23 所示，左舷连接器基座（图9）极限受拉承载力为704.1 MN，右舷连接器基座（图9）为714.4MN。两个参考点到达极限受压状态时的位移均达到60.8 mm。基座与连接器连接处应力较大，最先达到屈服破坏。

3.5.3 Z 方向向上

模型一和模型二采用与3.5.2 节同样的方法获得载荷—位移曲线。

模型一的载荷—位移曲线如图24 所示。连接器基座的极限承载力为124.7 MN，远远高于预报的20 MN，此时参考点的位移为0.3 m。在计算过程中，随着参考点强迫位移的增加，最先达到屈服极限的部位是立柱与上箱体底甲板连接处。

图23 载荷—位移曲线图（模型二）Fig.23 Loading-displacement of model 2

图24 载荷—位移曲线图（模型一）Fig.24 Loading-displacement of model 1

图25 载荷—位移曲线图（模型二）Fig.25 Loading-displacement of model 2

模型二的参考点的载荷—位移曲线，如图25 所示。左舷连接器基座极限承载力为113.2 MN，右舷连接器基座极限承载力为116.3 MN，远高于预报值20 MN。

3.5.4 模型一和模型二在不同方向的极限承载能力比较

两种模型的连接器基座在不同方向的极限承载能力如表6 所示。

表6 两种模型不同方向极限承载力Tab.6 Ultimate bearing capacity of different direction of two models

由表6 可知，两种模型计算获得的连接器基座不同方向的极限承载力相差不大。X 方向受拉或受压时，最先受到破坏的是基座与连接器连接部位；Z 方向向上受拉时，最先破坏的是立柱与上箱体底甲板连接处。不管是受到X 方向还是Z 方向的力，连接器基座的极限承载能力都远大于预报值。Z 方向的力对支座位移的影响较大，对立柱与上箱体底甲板连接处的强度要求高。

4 结 语

本文以包含连接器基座的上箱体为研究对象，选取包含单个连接器基座和两个连接器基座的上箱体局部结构作为模型进行静强度和极限强度分析，得到的主要结论如下：

（1）进行连接器静强度分析时，两种模型的连接器基座整体Von mises 应力都不大，但存在两处相同的高应力区，即基座与连接器连接部位，立柱与上箱体底甲板连接部位。两种模型在基座与连接器连接处的应力相差不大，而模型二在立柱与上箱体底甲板连接处应力相比模型一要大。在载荷方面，X 方向的力对于基座与连接器连接处应力影响较大，Z 方向的力对立柱与上箱体底甲板连接处应力影响较大，Y 方向的力对基座整体受力影响不大，几乎可以忽略。当三个方向的力同时施加在基座上时，结构应力最大。由于模型二比模型一尺寸大，柔度增加，因此变形相对较大。

（2）进行极限强度分析时，两种模型在不同方向的极限承载能力相差不大，且远大于各个方向载荷的预报值，连接器基座具有较大的结构强度储备，其中X 方向的强度储备大于Z 方向，能承受基本模块之间的挤压。X 方向受拉或受压时，基座与连接器连接部位最先达到材料屈服极限；Z 方向向上受拉时，立柱与上箱体底甲板连接处最先被破坏。Z 方向的力对支座位移影响较大，对立柱与上箱体底甲板连接处的强度要求更高。由于模型二尺寸大，柔度大，所以计算过程中变形更大。