中国流域降水数据的空间插值方法评估

2019-05-13

人民长江 2019年4期

(北京师范大学全球变化与地球系统科学研究院，北京 100875)

区域降水数据对生态评价、灾害风险管理、水文建模、植被分布和生态演变等研究领域具有重要价值[1-3]。气象站通过长期观测积累了大量的降水数据，但这些数据仅代表站点所在地区的降水状况，进行大范围降水研究时仍有所不足。对气象站的降水观测数据进行空间插值处理是获得降水空间分布特征最直接有效的方法，其精度和分辨率一般优于遥感反演和模式模拟[4-6]。空间插值效果受站点数量和分布的影响[7-8]，但由于技术和社会经济条件的限制，观测站点的数量有限且空间分布不均匀，地形复杂的偏远地区观测数据难以获取。所以当研究区域降水分布时，需要对空间插值方法进行评估，选择合适的插值方法将有限的站点数据快速、准确地转换为面状的区域降水信息[9]。在目前的研究中，空间插值方法可被分为确定性方法和地统计法[10]。确定性方法是基于已知点的信息及其相似程度，采用曲面对样本空间分布进行拟合，常用方法包括多项式法、反距离权重法、样条函数法等[11-12]；地统计方法利用样本点的统计规律，将样本点间的空间自相关性定量化分析，从而在未知区域构建空间结构预测模型，最具代表性的方法为克里金插值法及其变种[13]。上述空间插值方法各具优缺点，但目前关于这些方法在不同应用领域和不同研究区域的适应性分析还有所欠缺。对于不同应用领域和研究区域，同一降水插值模型的应用效果可能表现不一，不存在全部适用的最优插值方法。因此，根据研究区域的气象站点分布情况和地形流域特征选择最优的插值方法具有实际研究价值[14]。

我国幅员辽阔，气象观测站点较多但分布不均。本文以中国2 160个气象站点在1981～2010年间的降水观测数据为研究基础，对比分析不同空间插值方法的精度和适用性。为分析流域特征对最优降水空间插值方法的影响，本文从中国的DEM数据中提取地形因子和流域水系，并以黄河流域、长江流域和珠江流域为研究区域，探讨在研究三大流域的降水空间分布时的最优空间插值方法。

1 数据和方法

1.1 数据来源

本文选取的降水资料来源于中国气象局，包括2 160个气象站点在1981～2010年间逐日的降水量数据以及站点的经纬度、高程信息。为保证插值效果，在预处理阶段对站点数据进行了严格的质量控制，在筛选后共剩下1 915个站点用于插值，其分布如图1所示，中东部密集，而西北部较为稀疏。本文采用中国500 m×500 m网格的DEM数据进行流域划分，最终生成我国水系河网和集水流域，进一步结合中国河流矢量图，划分出黄河流域、长江流域和珠江流域。

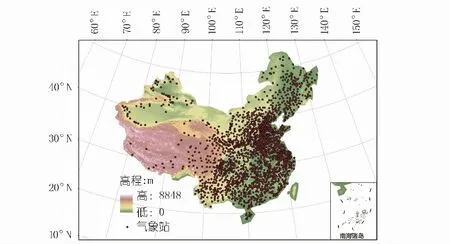
图1 中国DEM及气象站点分布Fig.1 DEM and meteorological site distribution in China

1.2 数据适用性分析

在进行空间插值之前需要考虑样本间的空间关联性，一般假设样本服从正态分布，且在空间上存在相关性[15]。所以本文首先对降水数据进行了空间自相关性分析和数据分布检验。

空间自相关性分析衡量的是样本点在同一分布区内潜在的相互依赖程度。受区域相互作用和空间扩散作用影响，相邻区域的降水分布不是相互独立的。在分布空间中，若相邻区域的降水值相近，则表现出一定的相关性；反之，则满足随机或独立分布[16]。空间自相关性可根据莫兰指数(Moran′s I)值判断，其取值范围为-1～1。Moran′s I值为正代表正相关，为负代表负相关，绝对值反映相关程度，接近于0表明相关性弱[17]。本文采用ArcGIS的空间分析工具，基于反距离加权的欧氏距离法，算得中国1 915个气象站点30 a降水数据的莫兰指数为0.735，表明该降水数据具有较高的空间自相关性。

我国的降水分布趋势为东南高，西北低。在使用克里金插值法前需要移除数据的固有趋势，以使插值结果更准确。所以本文采用趋势分析工具识别输入降水数据集的分布趋势，对降水数据进行Kolmogorov-Smirnov检验。检验结果表明该降水数据总体满足正态分布假设，故在插值处理前无需进行数据变换处理。用SPSS软件对站点高程和年降水量进行相关性检验，结果表明站点的年降水量与其高程显著相关。

1.3 空间插值方法

传统空间插值方法仅考虑对空间位置的加权，全局多项式法和局部多项式法即是采用一个或多个多项式对空间降水分布进行回归拟合[18-19]，而反距离权重法[20]则是根据距离的远近进行加权，距离越近的观测点赋予的权重越大。地统计法即克里金法，以统计理论为基础，用一个统计模型来拟合观测数据的分布，并通过使预测误差最小化，来达到最优的拟合效果[21]。通过构建不同的假设模型和半变异函数，克里金插值法形成了各种变种，包括普通克里金、简单克里金、泛克里金和经验贝叶斯克里金等[22-23]。径向基函数法类似于地统计法，但不要求数据分布满足任何先验假设[24-25]。本文采用上述8种空间插值方法，对我国1 915个气象站点的降水量数据进行插值处理。上述过程利用GIS的空间分析扩展模块实现，具有速度快、精度可靠、操作方便等特点。

2 降雨量空间插值

本文采用交叉验证方法对插值结果进行精度评定，即首先移除一个站点数据作为测试样本，然后利用其他站点的数据对该站点进行插值预测，并将预测值和实测值进行比较[26]。精度评价采用的指标是预测误差的均值(Mean)和均方根(RMS)，其计算方法见公式(1)～(2)。均值反映降水趋势，而均方根值反映预测值与实测值之间的接近程度，即预测的准确性，应尽可能小[27]。

(1)

(2)

式中，Mean为平均误差，RMS为均方根误差，n为观测点数，poi和pei分别为观测点i处降水量的观测值和预测值。

2.1 中国区域最优降水量插值方法

本文以筛选后的1 915个气象站点1981～2010年间的年平均降水量为数据源，选取了反距离权重法、径向基函数法、全局多项式法、局部多项式法、普通克里金法、简单克里金法、泛克里金法以及经验贝叶斯克里金法8种空间插值方法，对我国的降水数据进行插值。插值结果及精度如图2和表1所示。

降水量的空间插值需要综合考虑地形、流域、高程、站点数量和分布等因素，对不同流域最适插值方法的研究具有较强的实际应用价值。基于此，本文在中国降水最优插值方法的基础上，采用同样的方法，对各大流域降水的最优空间插值方法进行评估。

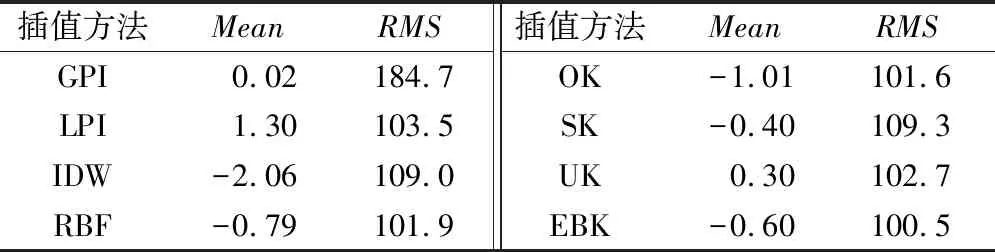
表1 中国降水量空间插值精度验证Tab.1 Accuracy of precipitation spatial interpolation in China

2.2 三大流域最优降水量插值方法

本文选择黄河流域、长江流域和珠江流域进行分析。按照三大流域对气象站点进行分类，站点分布如图3所示。黄河流域、长江流域和珠江流域分别包含263，634，140个气象站点。

对三大流域分别采用前述8种方法进行空间插值处理，插值结果和精度验证的结果如图4～6和表2所示。

3 结果分析与讨论

表1的精度验证结果表明，全国范围内经验贝叶斯克里金插值法取得了最优结果。而由表2可知，三大流域中，黄河流域泛克里金法最优；长江流域普通克里金法最优；珠江流域径向基函数法最优。

采用经验贝叶斯克里金法对中国的降水数据进行空间插值，可得到中国的降水量分布(见图7)。分析该降水量分布图可知，我国的年降水量存在较大的空间变异性，各区域的降水量差异悬殊。年降水量呈现由东南沿海向西北内陆逐级减少的分布趋势，年降水量最高处可达2 530 mm，最低处仅为7.2 mm。其中，东南沿海地区的年降水量可达1 600 mm，部分山区的年降水量甚至可达2 000 mm，而西北部地区的年降水量多在400 mm以下。

图3 三大流域站点分布Fig.3 Site distribution map of three major river basins

表2 三大流域降水量空间插值精度验证Tab.2 Accuracy of precipitation spatial interpolation in three river basins

图2 中国年降水量的8种方法空间插值结果Fig.2 The precipitation interpolation results of eight methods in China

图4 黄河流域降水量插值结果Fig.4 Precipitation interpolation results in Yellow River Basin

图5 长江流域降水量插值结果Fig.5 Precipitation interpolation results in Yangtze river basin

图6 珠江流域降水量插值结果Fig.6 Precipitation interpolation results in Pearl River basin

本文采用200，400，800 mm等降水量线，划分出中国的干旱区、半干旱区、半湿润区和湿润区，划分结果如图8所示。图8的干湿区划分是基于中国1981～2010年平均降水量数据的最优空间插值方法，由西北向东南显示出干旱区到湿润区的阶梯变化。该区划图相对较新且结果较为准确，对我国的农业生产、区域防控、生态保障等方面都具备重要的指导和参考意义。

分流域来看，黄河流域的年降水量呈现明显的阶梯状分布，降水量由南向北递减，流域内年降水量最高为895 mm，最低为135 mm。长江流域的降水总量丰富，空间分布趋势为东南向西北递减，流域内年降水量最高为1 988 mm，最低为340 mm。珠江流域降水总量丰富且表现出较高的空间异质性，空间分布的大致趋势为由东向西递减，流域内年降水量最高为2 179 mm，最低为812 mm。

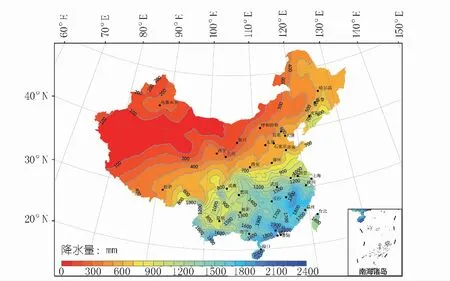
图7 中国年降水量分布Fig.7 Distribution of annual rainfall in China

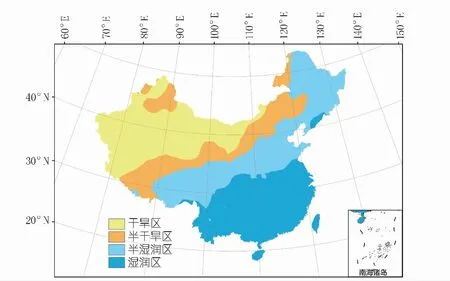
图8 中国干湿区划分Fig.8 Division of wet and dry area in China

为研究不同流域的最优插值方法对区域降水量分析的借鉴意义，选取三大流域流经的诸省市进行验证试验，实验结果如表3所示。

表3 三大流域降水最优空间插值方法验证Tab.3 Verification of optimal spatial interpolation method for precipitation

南宁和柳州位于珠江流域，其最优插值方法为径向基函数法，且优势较为明显；重庆和成都位于长江流域，其最优方法为普通克里金法，次优方法为经验贝叶斯克里金法；而处于黄河流域的郑州和呼和浩特市由于气象站点较少，普通克里金法、简单克里金法和泛克里金法的差异很小，均可视为最优方法。三大流域的最优插值方法与流域流经省市的降水最优插值方法表现出高度一致。三大流域流经的省市众多，覆盖我国主要的国民经济发展区域，研究结果表明不同流域的最优插值方法对区域降水量分析具有较高的借鉴意义和参考价值。