金沙江白格堰塞湖溃坝洪水演进高性能数值模拟

侯 精 明，马 利 平，陈 祖 煜2，齐 文 超，王 琳

(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048; 2.中国水利水电科学研究院，北京 100038)

堰塞湖是由滑坡、地震、泥石流等因素导致河道阻塞而形成的湖泊[1]。2018年10月10日22：06，西藏自治区昌都市江达县和四川省甘孜藏族自治州白玉县交界处发生山体滑坡，堵塞金沙江干流河道，形成堰塞湖。10月12日17：20，堰塞湖开始漫顶溢流，10月13日9:00，湖水水位下降20多米，溃坝隐患完全消除，10月13日20：00堰塞湖险情基本排除。通过对无人机拍摄的三维点云图进行测量(见图1)，得到堰塞体右岸被冲出的梯形水槽顶宽约160 m，底宽约70 m，深约55 m。2018年11月3日17：40，原滑坡地点发生二次滑坡，由于二次滑坡的土石方堵塞了初次滑坡后自然泄流冲出的水槽，同时在初次滑坡的土石方上再堆积，致使堰塞坝高度升高，危险增加。2018年11月12日10：50，人工开挖的泄流槽开始过流，2018年11月15日08：00，堰塞湖水位基本稳定，险情缓解。

堰塞湖形成后，由于阻塞河道的堆积物颗粒松散，且堰塞体没有泄洪设施，在上游不断来流、湖水位持续升高的条件下，堰塞体溃坝风险逐渐升高[2]。为减小堰塞体溃决后对下游造成的灾害损失，准确计算溃坝流量及下游洪水演进过程就显得尤为重要。目前，比较经典且使用较多的溃口流量计算模型有DAMBRK[3]、BEED[4]、BREACH[5]模型等。张大伟[6]等基于物理试验研究了两组粒径差别明显的砂样形成的堰塞坝溃坝过程，并建立了具有物理意义的概念性溃口流量计算模型；在洪水演进方面，杨志[7]等采用侧向连接方式，建立了一维河道二维淹没区耦合模型，模拟研究了黑河金盆水库溃坝洪水演进过程，但由于溃坝水流具有明显的二维特性，且流态复杂，一维河道模型并不能准确描述该过程；肖潇[8]等基于非结构网格，采用有限体积法建立了蓄滞洪区洪水演进数学模型；王晓玲[9]等针对溃坝洪水在复杂淹没区域中的演进过程，建立了耦合VOF法的三维紊流数学模型，但该模型计算效率比较低，模拟8h的洪水演进过程CPU耗时480 h。

为高效高精度地模拟溃坝洪水演进过程，本文采用溃口演变模型DB-IWHR计算溃口流量过程，并采用基于GPU加速技术的二维水动力模型模拟金沙江白格堰塞湖溃坝洪水演进过程。通过与下游叶巴滩及苏洼龙电站断面实测流量过程进行对比，证明了该模型可用来模拟计算堰塞湖溃坝洪水演进过程。

图1 初次滑坡后堰塞体三维点云图Fig.1 Three-dimensional point cloud map after initial landslide

1 模型简介

1.1 溃口演变模型

采用中国水科院陈祖煜等于2014年提出的溃口演变模型DB-IWHR[10]计算溃口流量。该模型主要包括溃口流量计算和溃口扩展两部分。

溃口流量采用宽顶堰公式进行计算，公式如下：

Q=C1C2B(H-z)3/2

(1)

C2=1.0-27.8(m-0.67)3

(2)

(3)

式中，Q为溃口流量，m3/s；C1为流量系数，建议取值范围为1.43～1.69 m1/2/s[11]；C2为考虑尾水淹没的系数；B为溃口宽度，m；H为水库水位，m；Z为溃口底高程；h为溃口水深,m。

溃口扩展过程为岩土工程中已经被广泛接受的简化的Bishop法。通过搜索可能的滑裂面，从而得到下切深度[12]。

1.2 洪水演进模型

1.2.1控制方程

本文应用具有守恒格式的平面二维浅水方程(简称SWEs)来模拟溃坝洪水的演进过程，忽略了运动黏性项、紊流黏性项、风应力和科氏力。二维非线性浅水方程的守恒格式可用如下的矢量形式[13]来表示：

(4)

(5)

式中，q为变量矢量，包括水深h，两个方向的单宽流量qx和qy；g为重力加速度，u和v分别为x、y方向的流速；F和G分别为x、y方向的通量矢量；S为源项矢量；zb为河床底面高程，Cf=gn2/h1/3为谢才系数，n为曼宁系数。

1.2.2数值方法

本模型采用Godunov格式的有限体积法求解二维浅水方程。单元界面通量应用HLLC格式的近似黎曼求解器求解[14]。通过静水重构来修正干湿边界处负水深。底坡源项使用模型作者提出的底坡通量法处理。摩阻源项的计算使用半隐式法来提高稳定性[15]。采用二阶显式Runge Kutta[16]方法进行时间步长的推进。构造具有二阶时空精度的MUSCL型格式，有效解决复杂地形干湿界面处的负水深和伪高流速等现实中不存在的物理现象所造成的计算失稳和物质动量的不守恒问题。因溃坝洪水演进过程模拟一般尺度较大，为提高计算效率，模型采用GPU并行计算技术实现高速运算[17-18]。

2 模型构建

2.1 研究区域概况

本研究区域概况已于前节描述。本文模拟研究的范围为从白格堰塞体至下游235 km长的河段(见图2)。

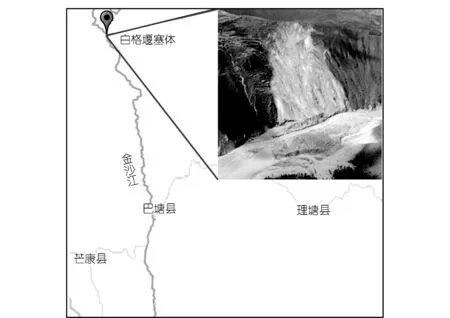
图2 研究区域位置Fig.2 Regional map

2.2 溃口流量计算

采用溃口演变模型DB-IWHR对“10·10”与“11·3”两次堰塞湖溃坝事故进行模拟计算，具体参数见表1，模拟计算结果见图3。

2.3 水动力模型设置

模型的输入资料为地形数据、入流数据等。地形资料为从白格堰塞体到苏洼龙段的数字地形高程(DEM)数据，由于该区域精细地形难以获取，故基于美国对地观测卫星Terra提供的30 m分辨率DEM地形数据(见图4)，利用遥感影像提取河道宽度，并下挖一定深度概化出水下河道地形。研究区域高程落差大约500 m，河段长235 km，平均坡度0.002，平均宽度300～600 m。模拟网格462万个，其中叶巴滩段87万个，苏洼龙段375万个。入流数据为DB-IWHR溃坝模型计算的两次溃坝事故的溃口流量过程。上游边界为入流边界，下游边界为自由出流的开边界，其余边界定义为封闭边界。由于金沙江断流后下游河道仍有大约200 m3/s的流量，故给予河道200 m3/s的恒定流量作为初始条件。根据现场实际情况选取曼宁系数为0.02[19]，库朗数为0.50，共模拟40 h洪水演进过程。

图4 研究区域数字地形高程Fig.4 DEM of the study area

表1 金沙江白格堰塞湖溃口流量计算参数Tab.1 Calculation parameters of dam break discharge at Baige barrier lake in Jinsha River

图3 所选模拟溃坝洪水过程线Fig.3 Selected simulated inflow hydrograph of the dam break

3 模拟结果分析

3.1 “10·10”白格堰塞湖结果分析

针对“10·10”白格堰塞湖溃坝事故，应用二维水动力模型对堰塞体下游235 km长的河段进行洪水演进模拟。由于下游叶巴滩与苏洼龙处都有在建或已建成的水电站，各水电站的防洪安全是人们最为关心的，故选取这两处的流量过程进行模拟对比。其中叶巴滩距堰塞体54 km，苏洼龙距堰塞体224 km。模拟耗时61 min，模拟结果见图5。从图中可看出，叶巴滩处模拟的流量过程在上升和下降阶段都比实测快，洪峰流量比实测大5 247 m3/s，洪峰出现时间基本一致，误差主要在于溃口演变模型DB-IWHR模拟计算的溃坝流量峰值比实测要大；苏洼龙处模拟的流量过程与实测流量过程吻合较好，洪峰流量比实测大220 m3/s，在流量过程下降阶段比实测要快。

图5 “10·10”溃坝洪水演进模拟与实测流量过程Fig.5 Simulated and measured discharges of the "10·10" dam break flood propagation

3.2 “11·3”白格堰塞湖结果分析

二维水动力模型对“11·3”白格堰塞湖溃坝洪水演进模拟的结果见图6，模拟耗时74 min。

图6 “11·3”溃坝洪水演进模拟与实测流量过程Fig.6 Simulated and measured discharge of the "11·3" dam break flood propagation

模拟研究结果表明，在叶巴滩处，模拟的洪峰流量比实测小1 012 m3/s，流量过程整体延迟2 h；在苏洼龙处模拟流量过程与实测吻合较好，洪峰流量比实测小614 m3/s，在下降阶段比实测稍大。在叶巴滩处产生误差的主要原因在于地形数据的精度不高，难以准确描述主要河道地形，尤其是水下地形。

4 结 论

应用二维水动力模型对“10·10”与“11·3”金沙江白格堰塞湖溃坝洪水演进进行模拟，通过将模拟流量过程与下游叶巴滩、苏洼龙电站断面处的实测流量过程进行对比，可得到如下结论。

(1) 对于无高精度地形资料的山区，该二维水动力模型可以较好地模拟溃坝洪水的演进过程。在对“10·10”与“11·3”两次溃坝洪水的模拟中，苏洼龙处模拟结果较好，而叶巴滩处误差较大，主要原因是该处所用的terra 地形和概化的河道地形数据精度不高，较实际有较大偏差。

(2) 在堰塞体至苏洼龙共462万网格的地形数据上进行洪水演进模拟，共模拟40 h洪水演进过程，由于该二维水动力模型基于GPU并行计算技术进行加速，采用英伟达RTX 2080 GPU，两次溃坝洪水演进模拟耗时分别为61 min和74 min，可见该二维水动力模型在模拟洪水演进时是非常高效的，对于争分夺秒的洪水应急抢险事件，该模型可实现快速预测，为决策者提供有力数据支撑。