不同空间分辨率遥感数据识别湖泊的误差分析
2019-05-13141
141
(1.安徽省·水利部淮河水利委员会 水利科学研究院,安徽 合肥 230088; 2.水利水资源安徽省重点实验室,安徽 合肥 230088; 3.清华大学 地球系统科学系,北京 100084; 4.安徽省大禹水利工程科技有限公司,安徽 合肥 230088)
湖泊是陆地水圈的重要组成部分,在维持陆地表层系统生态平衡、减轻干旱和洪涝灾害、促进人类文明的发展等方面发挥着不可替代的作用[1]。湖泊水面的扩张与收缩直接影响湖泊的各种功能[2],甚至诱发区域生态系统演变。因此,实时准确地提取湖泊水域面积,对于揭示自然因素、人类活动对湖泊的影响,以及保护湖泊水资源和生态环境等意义重大[3]。卫星遥感技术的发展,将人类对地球表层的理解推进到一个新的阶段,同时也给快速、大范围、全面深入的湖泊水域监测提供了新的途径,已成为近年来湖泊水域面积提取的重要技术手段[4~5]。
不同空间分辨率的遥感影像所体现的地物特征、所承载的地物信息量不同。另外,不同湖泊的地貌、水文等自然要素不一样,并且易受周边人类活动的影响,因而呈现出复杂多变的集合形态。利用不同空间分辨率遥感影像进行湖泊制图会存在精度上的差异。如何衡量和消除这些差异具有很强的现实意义和价值,是亟待解决的重要科学问题。另外,不同空间分辨率湖泊面积提取精度是湖泊遥感制图数据源选择的基本依据。目前,已经有一些学者就空间分辨率对水体遥感提取的影响做了相关的研究[6-11]。张毅,陈成忠等[8]利用TM影像分别采用最邻近法和像元聚合法,获取分辨率逐步降低的不同分辨率影像,探讨水域面积随影像分辨率降低的变化趋势及其误差特征,其研究结果证明空间分辨率是影响鄱阳湖水体提取精度的重要因素之一;因为空间分辨率的大小会影响提取水体的精度。于欢、张树清等[9]主张采用像元分解及多源遥感数据融合技术来提高水体信息提取精度;曹广真,卢乃锰等[10]分析不同面积湖泊随空间尺度的变化,证明了影像分辨率越低,湖泊面积提取的偏差越大,尤其是面积较小的湖泊。徐蓉、张增祥等[11]人以理想化的椭圆形、三角形和六边形为例,推算并验证了不同空间分辨率遥感影像提取面积间的关系,但其实验湖泊形态较为简单,未能考虑到较为复杂的湖泊,代表性较差。
此外,随着分辨率的降低,通过地形数据提取的高程数据会发生变化,流域地形也会随之逐渐变得平坦,流域的平均坡度、河网密度以及河网长度等也在逐渐减小。熊金国、王世新等[12]发现,在低分辨率图像中,水域提取精度取决于观测区域的水体景观格局分布,此外在分析高分辨率下水体的面积比例、周长以及高分辨率和低分辨率水体面积误差之间的关系时,斑块面积很小且很破碎的区域产生的误差较大,但当斑块面积比例高且周长相对较低时,误差就很小。Evan A. Lyons,Sheng Yongwei等[13]发现空间分辨率、辐射度和时序因素会影响水体遥感提取的精度。湖泊的几何形态是影响湖泊制图和面积估算的一个潜在因子,但是目前这方面的研究还较为欠缺。因此,本文选取安徽的若干湖泊作为研究对象,使用不同空间分辨率的遥感数据对该问题展开研究和讨论。
1 研究区域概况和数据预处理
1.1 研究区域概况
安徽省地跨长江、淮河、新安江三大流域,境内河流湖泊众多,水资源丰富,但是南北分布不均,境内洪涝、干旱灾害频发,其中1954,1963,1991,1998,2003,2005,2007,2008,2016年等年均发生大规模的洪灾,带来了人员伤亡和难以估计的经济损失。实时监测安徽省境内湖泊的动态变化,掌握省尺度的水资源状况,有助于进行洪涝及干旱等灾害的预警,提高水文水资源相关决策的科学性和合理性。
本文选取安徽省54个湖泊作为研究对象(见图1),研究范围介于东经114°54′~119°37′,北纬29°41′~34°38′之间,位于暖温带与亚热带的过渡带,地处长江和淮河中下游,湖泊众多。该区域经济快速发展,人类活动对湖泊的影响日趋增强。以这54个湖泊为例,探讨湖泊的形态复杂度是否对湖泊制图精度有影响。
1.2 数据源
本研究选取2016年2月份前后的GF-1/WFV(GF-1/Wide Field View),MODISHKM(Moderate-Resolution Imaging Spectroradiometer Half Kilometers),MODIS1KM(Moderate-Resolution Imaging Spectroradiometer 1 Kilometers)和Landsat-8/OLI(Landsat-8/Operational Land Imager)遥感影像共17景,其中18 m的高分一号6景、500 m的MODISHKM 1景、1 000 m的MODIS1KM1景和30 m的Landsat8数据9景。所有选取的遥感影像质量较好,湖泊上空基本无云覆盖。由于该区域湖泊面积的枯水期和丰水期差异明显,因此,本文尽量选用相近观测时间的遥感影像(见表1,获取时间精确到年月日),以减少湖泊季节变异引起的伪变化。
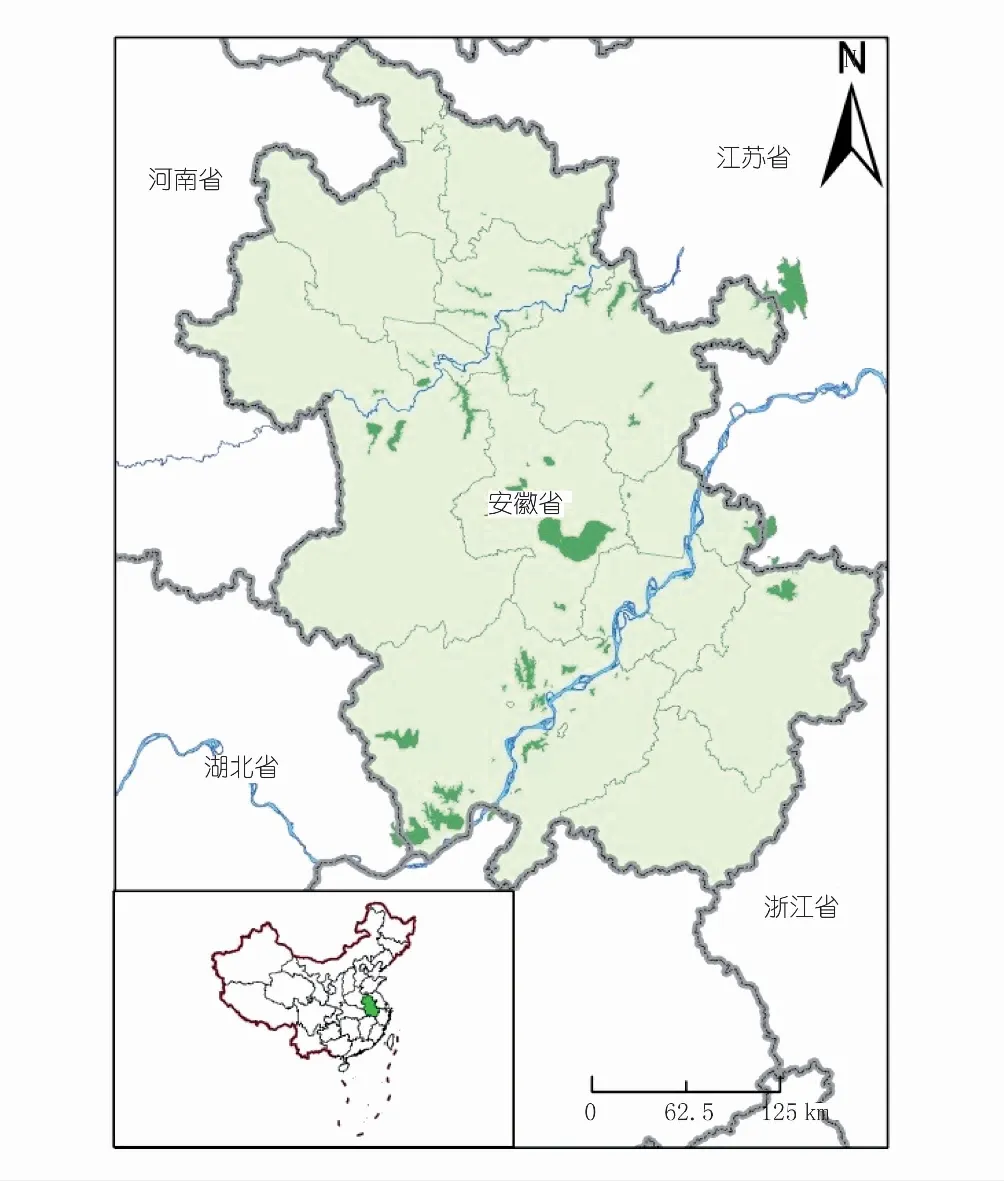
图1 实验湖泊空间分布Fig.1 The spatial distribution of lakes for the study
1.3 方 法
本研究的技术路线为:在数据预处理的基础上,利用经典的NDWI(Normalized Difference Water Index) 方法提取遥感影像中的水体信息,以历史统计湖泊水域岸线(历史统计湖泊水域岸线:结合2014年安徽省第一次水利普查成果,采用高分一号卫星数据,安徽省(水利部淮河水利委员会)水利科学研究院河湖监测遥感中心逐月份半自动提取的湖泊枯水季矢量数据的水边线中心线)外1 km范围为界,对研究区54个湖泊进行裁剪得到各湖泊的潜在空间范围,以高分一号数据的高分辨率制图结果作为参考数据,计算landsat8、MODISHKM和MODIS1KM相对参考数据的误差,以高分一号湖泊提取结果的分形维数值衡量湖泊水域的复杂情况,分析湖泊形态的复杂度对不同分辨率遥感影像提取得到的湖泊影像。具体的技术路线如图2所示。
整个实验过程采用全自动化的方式,以减少人为因素的干扰。使用ENVI5.2软件对高分一号数据 (GF1/WFV)、MODISHKM和MODIS1KM进行数据预处理,包括辐射校正、几何校正和正射校正。
在高分一号数据中,使用B2波段(中心波长0.56 μm)和B4波段(中心波长0.797 μm),在landsat8数据中,抽取B3波段(波谱范围0.525~0.600 μm)和B5波段(波谱范围0.845~0.885 μm),在MODISHKM和MODIS1KM数据中,抽取B2波段(波谱范围0.841~0.876 μm)和B4波段(波谱范围0.545~0.565 μm),利用绿光波段和近红外波段进行NDWI指数[14]计算以突出水体信息,抑制非水体信息,计算公式为
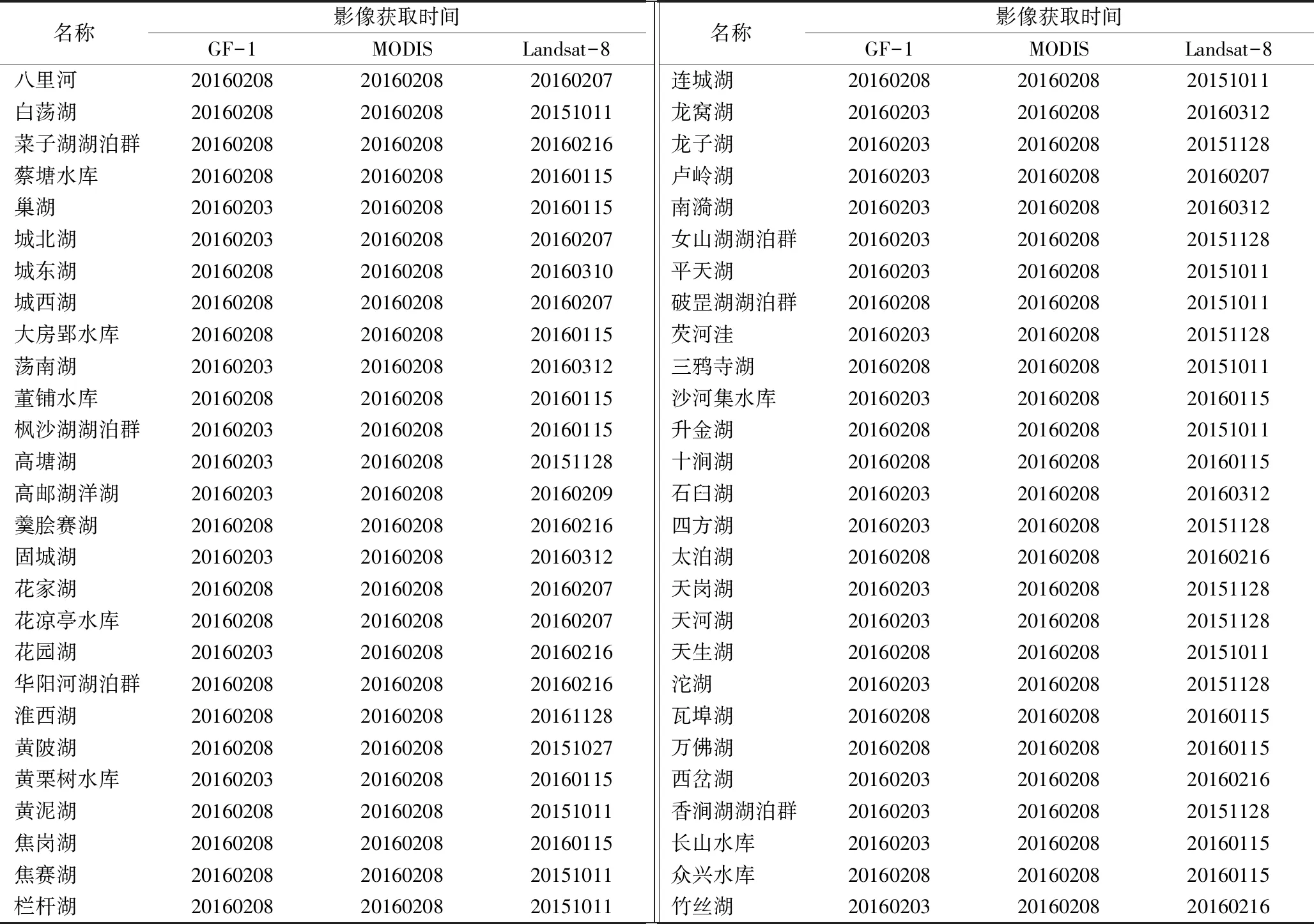
表1 各湖泊GF-1验证数据与Landsat-8、MODIS试验数据Tab.1 Summary of studied lakes with observation time of GF-1、Landsat-8 and MODIS data

(1)
式中,Green和Nir分别代表绿光波段和近红外波段。研究过程中,为避免人为因素影响分割阈值的选取,参考同类研究成果[15],对于Landsat8、MODISHKM和MODIS1KM数据,均采用0作为分割阈值,即NDWI数值大于0对应像元的被划分为水体。实验中参考数据高分一号的分割阈值有3个,分别是利用大津算法[16-17](即最大类间方差法、OTSU )得到的阈值、灰度分割阈值1(20类)、灰度分割阈值2(25类),以衡量参考数据的变化对实验结果的影响。本研究定义以湖泊为中心区域及其1 km缓冲区范围为湖泊水域区域(见图3)。
本文选择面积误差RA、面积偏差比|RA|、错分率Er、漏分率Lr、Kappa系数和总体精度作为衡量制图精度的指标。
(2)
式中,A16表示基于GF-1/WFV提取的湖泊面积;A0表示基于其他数据提取的湖泊面积;F1表示相对于参考数据中的水体,将非水体像元错分为水体像元的面积;F2表示相对于参考数据中的水体,将水体像元误分为非水体像元的面积。

图3 NDWI分区域对比Fig.3 Comparison of NDWI maps of several sub-regions
采用经典的计盒维数方法计算每个湖泊的参考数据分形维数值DB,用来表征不同湖泊的形态复杂程度[18-19]。
(3)
式中,F为湖泊水体二值图像(见图5),NδK为与F相交的δK网立方体的个数,即覆盖图像中水体区域的网格的数目。将图像F进行c等分,δK为网格大小。
(4)
上式表明,δK为一个递减序列。以一系列 “网格大小”δK与相应的“覆盖网格数”NδK的数据对,进行线性回归分析,湖泊水体图像的分形维数值DB为直线斜率(见图4b中红色直线)。
2 结果与分析
2.1 湖泊面积提取精度与形状复杂度的关系
如图3所示,以八里河、董铺水库和万佛湖为例,利用各种空间分辨率的遥感影像进行湖泊提取,其中GF-1/WFV数据的NDWI分割阈值为灰度分割阈值1(值为0.250 37),提取结果见图5。由图5可见,空间分辨率的差异对湖泊提取结果有着明显的影响,随着影像分辨率的升高,提取结果的细节逐渐丰富,越接近实际湖泊形状,较粗的分辨率容易受混合像元效应的影响,造成湖泊面积的低估(忽略一些较小的水体)或高估(误识别湿地等陆地信息为水体)。
表2中,面积误差为水体面积与准确值(GF-1水体)之间的差异。图6展示了所选取的湖泊的分形维数与其湖泊面积误差、面积偏差比之间的关系。从表2和图6可以看出,随着湖泊形态复杂度的增大,即湖泊分形维数值的增大,Landsat-8/OLI、MODISHKMMODIS1KM提取的水体面积误差值和面积偏差比均逐渐减小,说明提取水体的精度逐渐增大。

图4 估算湖泊的分形维数Fig.4 The plot for estimating fractal dimension of lakes

图5 水体提取分区域对比图Fig.5 Comparison of lake maps for several sub-regions

表2 不同空间分辨率下不同湖泊的提取精度Tab.2 Statistics of extraction accuracies for different lakes with various spatial resolutions

图6 面积误差、面积偏差比与湖泊形状复杂度之间的关系Fig.6 Relationship between area error, area deviation ratio and morphological complexity of the lake
计算得到湖泊制图结果的错分率、漏分率、总体精度和kappa系数,发现对于landsat-8/OLI、MODISHKM和MODIS1KM三种数据,提取结果的错分率、漏分率和总体精度与湖泊形态复杂度之间无一致和明显的规律。图7展示了Kappa系数与湖泊形态复杂度之间的关系,可以看出随着湖泊分形维数值增大,Kappa系数呈现逐渐增大的趋势。综合多个制图精度的衡量指标,可以发现,湖泊形态复杂性确实影响其遥感制图精度。
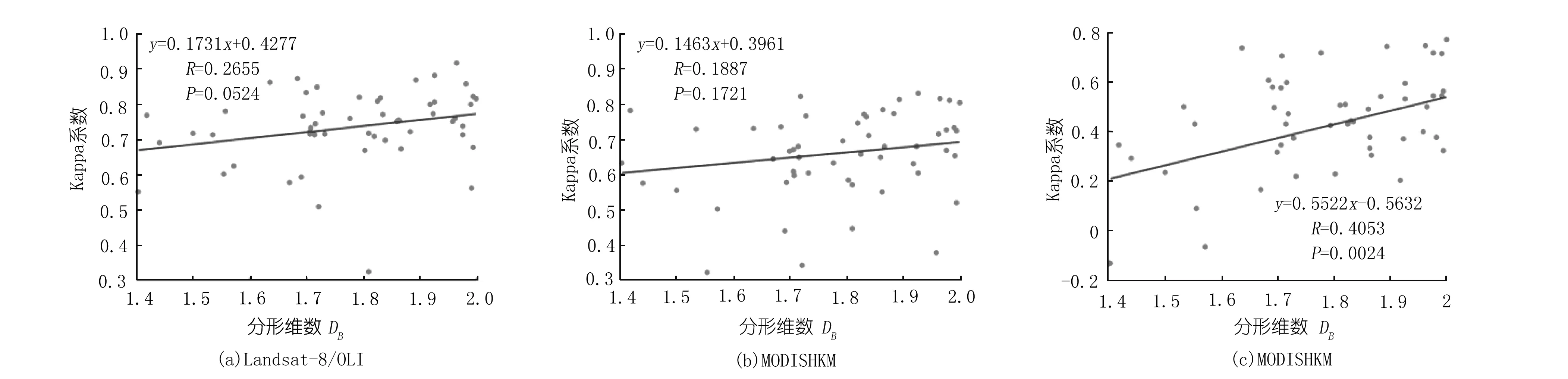
图7 Kappa系数与湖泊形状复杂度之间的关系Fig.7 Relationship between Kappa coefficient and lake morphological complexity
如图8(a)所示,湖泊的面积误差与其分形维数值表现出正相关性(R>0.35,P<0.01)。如图8(b)所示,湖泊的分形维数和总体精度、Kappa系数两个量之间也表现出较强的正相关性(R>0.45,P<0.05)。结果表明,本研究得到的结论对于不同空间分辨率的遥感数据都是成立的。
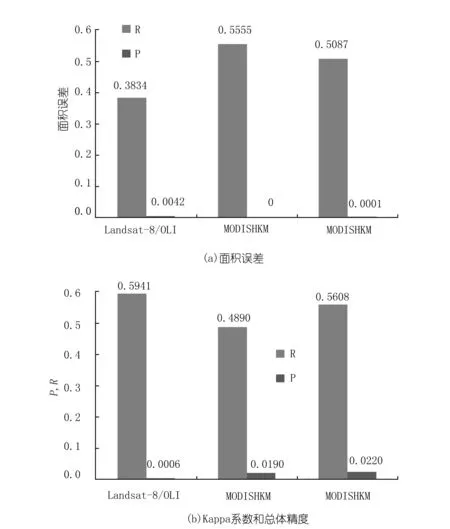
图8 分形维数与湖泊提取精度之间的关系Fig.8 Relationship between fractal dimension and lake extraction accuracy
2.2 结论可靠性验证
NDWI 的阈值主要取决于水和非水像元的比例组合,而这个比例往往容易受干扰,使得最佳阈值难以确定[14],这可能对研究的结论存在一定影响。研究采用GF-1/WFV数据结合NDWI阈值方法获得参考数据,以衡量阈值对实验结果的影响。因此,此处采用3种方式确定阈值以保证所得结论的可靠性:第1种是大津算法计算的阈值(值为0.196 10);第2种为前面提到的灰度分割阈值1,采用灰度阈值分割将NDWI图像分割为20类逐步确定的最佳阈值(值为0.250 37);第3种为采用灰度阈值分割将NDWI图像分割为25类逐步确定的最佳阈值——灰度分割阈值2(值为0.300 00)。不同的阈值确定方法所得的实验结果如表3所示。阈值分别设置为0.196 10,0.250 37,0.300 00时,P值略微增大,但均小于0.1,说明水体分割阈值对实验结果有轻微但不明显影响,并不影响实验结论,即湖泊遥感提取精度与其几何形态的复杂度确实存在明显的相关性。

表3 实验湖泊形态复杂度与提取精度的相关性Tab.3 Correlation between lakes morphological complexity and extraction accuracy
3 结 论
本文从实际应用需求出发,采用GF-1/WFV、Landsat-8/OLI、MODISHKM、MODIS1KM几种不同空间分辨率遥感数据,对安徽省54个湖泊进行遥感制图,选择面积误差、面积偏差比和Kappa系数等作为衡量遥感制图精度的指标,分析了湖泊提取精度与湖泊几何形态的关系。得到如下结论:
(1) 分形维数值越大,湖泊形态越复杂,提取结果的Kappa系数越高,面积误差和面积偏差比越小,制图精度越高。
(2) 遥感影像分辨率越高,湖泊识别结果的细节越丰富,湖泊制图结果的Kappa系数和总体精度越高,但对湖泊面积误差无明显影响。
本文对于湖泊遥感提取的误差做了一定探索性分析,有助于进一步研究其误差源和指导湖泊制图的数据选择。尽管本文针对湖泊及其几何形态的关系进行研究,其思路也可以扩展至其他空间地物如河流、海岸线等[19]。
