不同数据处理策略对Chl-a浓度预测精度的影响

(三峡大学 水利与环境学院,湖北 宜昌 443002)

水华是在温度、光照、营养盐等环境条件适宜时，藻类大量生长繁殖并富集成一定浓度，导致区域水体变色的现象，是水体富营养化的典型代表。水华暴发易引起明显的水质变化，严重阻隔生态能量的有效循环，破坏水体的生物多样性，已成为水环境治理中的难题[1]。叶绿素a含量常被作为特征指标用以预测藻类生长暴发，在水体理化性质和生物存量分析指标中占据重要地位[2]。研究藻类水华的暴发机制，分析水体中叶绿素a的时空变化规律，预测水华的时空分布，对水华及其生态影响的预警和防范都具有重大意义[3]。

利用实时监测数据，采用神经网络对水体中叶绿素a含量进行预测，是水体中叶绿素a含量预测的主要手段之一[4]，得到了广泛应用[5]，取得了比较有效的预测结果。例如Velo-Suarez等[6]在Andalucia的大西洋沿岸流域实现了对藻类的神经网络预测模型构建；Guallar等[7]在地中海Alfacs湾建立了对双鞭毛藻和硅藻的神经网络预测机制；赵文喜等[8]在中国海河干流完成了基于BP神经网络的叶绿素a含量预测短时预测研究，皆对相应流域的藻类生长趋势进行了有效预测。

输入数据的准确性对神经网络的预测精度有决定性的影响，但实时监测数据受各种随机因素影响，会存在异值点、数据缺失、数据不光滑等不符合物理规律的情况[9]，需要对原始监测数据处理，以提高数据质量及预测精度。相关研究表明，不同处理方法对预测精度影响较大。例如王亚宸等[10]在澳大利亚能源市场研究中，采用小波变换处理噪音数据，成功实现了维多利亚州电力负荷以及电价的高精度预测；Iliou等[11]在骨质疏松症预测案例中，应用了一种基于MLP分类器的新型数据处理方法，达到神经网络高效分类的目的。但数据处理对基于神经网络的水体叶绿素a含量预测精度影响方面尚没有专门研究。

因此，本文在实时监测数据基础上，分别采用3种异值点处理方法与2种数据光滑方法组合，讨论不同数据处理方法对主成分影响，研究神经网络的输入参数确定方法，选择5种神经网络输入参数组合，分析不同数据处理方案下神经网络预测精度，研究样本数据处理策略对基于神经网络的叶绿素a预测精度的影响，为提高基于神经网络的水华暴发预警技术的预警精度提供支撑。

1 数据预处理

1.1 数据来源

研究所采用的数据为研究水域2016年4月下旬到12月监测时段内的pH、氨氮(NH3-N)、电导率(COND)、水温(WT)、溶解氧(DO)、叶绿素a(Chl-a)、淡水蓝绿藻(AFA)、氧化还原电位(ORP)、气温(AT)、气压(AP)、相对湿度(RH)、降雨(Rainfall)及光强(Lux)13项实时监测数据，数据频率为每10 min1次。受多种因素影响，数据存在异常值，部分数据缺失，数据连续性及光滑性不足等问题(图1(a)中，氨氮监测数据存在异常值；图1(b)中，水温监测值连续性、光滑性不足)。

图1 监测数据异常分布示意Fig.1 Unusual distribution of monitoring data

1.2 异常值及缺失值处理

结合本次监测数据的采集频率及实际分布状态，本文依次尝试使用以下3种判据准则进行异常值处理。

(1) 拉依达准则[12](Pauta Criterion)，又称3σ准则，假设监测数据只存在随机误差，对数据计算出标准差σ，随机误差在指定概率区间(-3σ,3σ)的分布概率约为99.7%，监测误差超过指定概率区间就判定为异常值。

(2) 肖维勒准则[13](Chauvenet Criterion)，在监测数据中，临近时段的n次监测数据，如果某监测值xi与平均值x之差的绝对值大于标准偏差与肖维勒系数之积，则该监测数据为异常值。

(1)

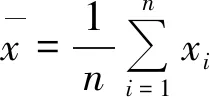
ωn=1+0.4ln(n)

(2)

针对藻类水华数据变幅较大的特性，肖维勒法剔除异常值时样本数需灵活取值；本文以样本数500为一组，肖维勒系数ω500=3.20进行异常值判断。

(3) 格拉布斯准则[14](Grubbs Criterion),监测值对应残差的绝对值满足下式时，判定监测值为异常值。

(3)

式中，g(n,a)为格拉布斯临界系数，与监测样本数以及显著水平有关，本文临界系数取g(100,0.05)=3.17，以样本数100为一组进行分批检验。

本文基于以上3种准则对监测数据进行异常值筛选处理。对于同一监测数据，3种准则选取评判的样本群体不同(σ=0.398 2，ω500=3.20，g(100,0.05)=3.17)，对应的判定结果亦相异，拉依达准则判定标准最为宽松，格拉布斯准则最为严格，肖维勒准则居于两者之间。此外，若该点监测数据为异常值，则当作缺失值进行处理。

常用缺失值处理方法有个案剔除法、均值替换法、热卡填充法、回归替换法、期望最大化法等。本文采用如下方法处理：同一时间点若单项监测数据缺失则采用均值替换法，若同时多项监测数据缺失则采用个案剔除法去除该时间点所有监测数据。

1.3 数据平滑滤波

水体的理化监测指标理论上应是光滑连续变化的，但受监测频次限制及外界随机因素干扰，数据光滑性常常不满足要求，需要利用平滑滤波方法处理。本文在异常值处理的基础上，分别采用临近加权平均法、局部多项式回归法[15]对监测数据平滑。

临近加权平均法中，以监测点i为计算中心，计算临近个点k的加权平均值作为监测数据xi对应的平滑值：

(4)

图2 监测数据平滑效果对比Fig.2 Smoothing effect comparison of monitoring data

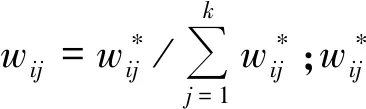
局部多项式回归，是基于最小二乘法原理在该点拟合回归的多项式代入值与监测值之差的平方和最小时，确定局部多项式回归效果最佳，平滑值计算公式如下：

j=-m,…,0,…,+m

(5)

本文采用纳什效率系数分析数据平滑效果：

(6)

对以拉依达准则、肖维勒准则和格拉布斯准则进行数据异值处理后得到的3组数据，分别进行临近加权平均、局部多项式回归处理得到6组数据变换预处理方案，方案中各监测指标以纳什效率系数不低于0.985作为平滑标准。各方案既有效消除了数据中的高频“噪音”影响，同时也尽可能地保持了数据原有的客观真实性，可以为后续研究提供数据支撑。部分数据平滑前后的对比如图2所示。

1.4 主成分分析

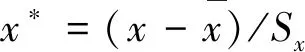
表1 不同数据处理方案主成分分析结果Tab.1 Principal component analysis results of different data processing schemes

注：1.“3σ”，拉依达准则；“Chauvenet”，肖维勒准则；“Grubbs”,格拉布斯准则；2.“AAv”，临近加权平均法；“SG”，局部多项式回归；3.基于特征值0.6；具有Kaiser标准化的正交旋转法。

以pH、氨氮、电导率、水温、溶解氧、叶绿素a、氧化还原电位、气温、气压、相对湿度、降雨及光强标准化后数据进行主成分分析，分析结果拟合度均达到85%以上。显然，不同数据处理方案得到的主成分也有区别，说明数据处理方案对主成分分析结果有一定影响。但总体而言占据优势的成分依次为：叶绿素a、气温、光强、气压、降雨、电导率、相对湿度；可将其作为叶绿素a含量预测输入参数。

2 基于BP神经网络叶绿素a预测模型构建

2.1 输入输出参数的选择

由于叶绿素a的含量与藻类的数量密切相关，在一定程度上能够反映水质状况，是判断水体富营养化的重要指标之一[18]，前文主成分分析表明，叶绿素a需为模型输入参数，才可保证模型的预报精度。需要定义新的输出参数，以预测下一时刻叶绿素a含量。鉴于此，定义单位时间内叶绿素a含量的变化量为平均生长率GR，用公式表示为

(7)

其中，GR为t1～t2时刻之间的平均生长率。

下一时刻叶绿素a含量，由下式计算：

(8)

2.2 BP神经网络结构设置及训练

适合的BP神经网络结构设置既能加快收敛速度，也能保证预测精度[19]。本文依据预测误差最小确定叶绿素a含量预测的BP神经网络隐含层为2层，隐含层神经元个数为12；隐含层采用learngdm阈值学习函数，输出层采用purelin传递函数；最大迭代次数1 000次，设置0.05的步长。有效数据11 000组，其中8 000组作为训练集，2 000组作为测试集，1 000组作为预测集。叶绿素a含量预测的BP神经网络结构图如图3所示。

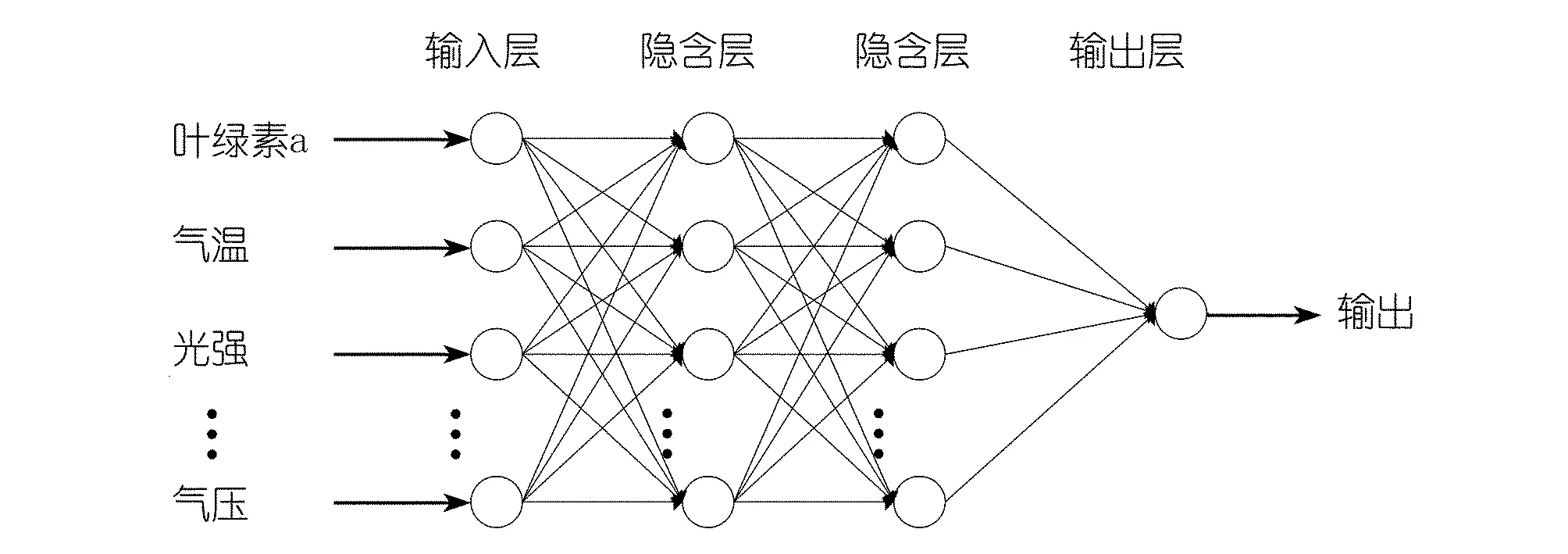
图3 BP神经网络结构Fig.3 BP neural network structure

研究不同数量输入参数组合对神经网络预测精度的影响，当参数输入数量相同时，以预测精度最好的组合作为该输入参数下的最优组合。以格拉布斯准则异常值处理组合局部多项式回归平滑处理数据为例，不同输入参数下叶绿素a含量预测值分布对比见图4。不同数量的最优输入参数组合，对叶绿素a含量均有较好的预测精度，说明影响叶绿素a含量变化的因子间不是相互独立的，各因子间存在交织作用。因此，关注主要影响因子，精简预测模型输入是提高叶绿素a含量预测效率的可行途径。

不同数量的最优参数组合预测精度如表2所示，对比主成分分析结果可发现，7参数下输入参数的最优组合与主成分分析结果相同，当输入参数减少时，去除的输入参数为主成分分析结果中权重最小的因子，主成分分析结果可用于指导神经网络输入参数选择；神经网络预测精度随着输入参数的增加而提高，将所有监测参数(13个)当作输入参数时，预测精度最高，可达0.994，相比4参数输入的0.986，预测精度有所提高，但提高程度有限。其中，4、13参数叶绿素预测效果对比如图5所示。

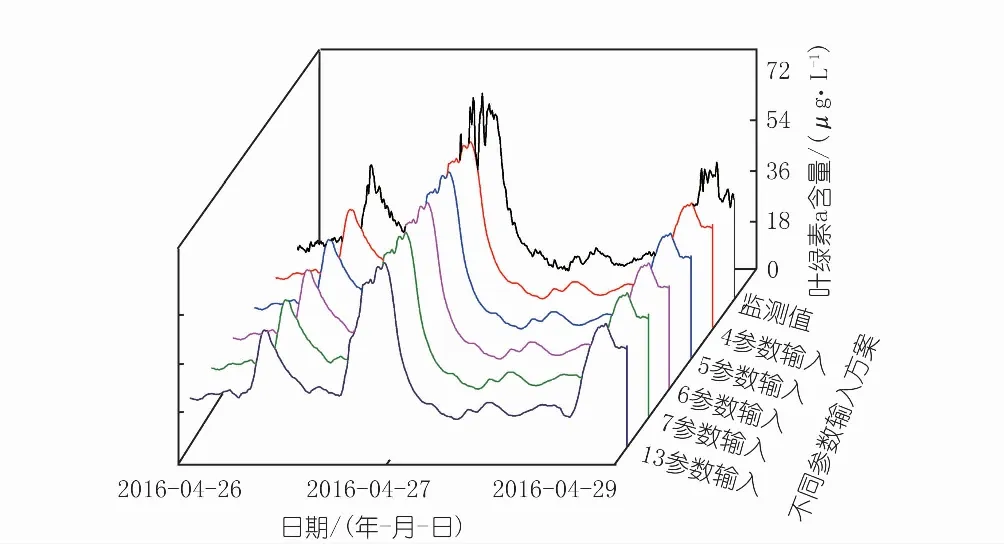
图4 不同参数输入下叶绿素a含量分布Fig.4 Distribution of Chlorophyll-a content under different parameters input

表2 不同输入参数组合的平均生长率预测精度Tab.2 Average growth rate prediction accuracy of different input parameter combinations

3 数据处理对预测精度影响

将3种异值点处理方法与2种数据光滑方法组合，结合原始数据，得到了7组数据处理方案，与5种输入参数数量方案组合，共可得到35种组合方案。针对每种数据处理方案，进行主成分分析，根据各影响因子权值，由小到大剔除输入参数，对BP神经网络训练，得到不同数据处理方案及不同输入参数组合下的预测精度结果，如表3所示。

采用原始数据进行预测时，预测精度普遍不高，如图6所示，预测精度不随输入参数增加而增加，说明原始数据存在干扰项，影响神经网络预测精度。

对比原始数据方案与数据处理后方案，在输入参数数目相同情况下，对数据进行处理可显著提高神经网络的预测精度，但不同的数据处理方法对其预测精度的提高程度不同。在采用临近加权平均法对数据进行平滑处理的条件下，不同数据异值处理方法对预测精度提高效果明显，但预测精度与输入参数数量间相关性较差，不同数据异值处理方法优劣无法确定，但以拉依达准则处理后得到的预测精度最高，为0.938。在采用局部多项式回归方法对数据进行平滑处理的条件下，不同数据异值处理方法对预测精度提高显著，预测精度与输入参数数量间相关性强，以格拉布斯准则处理效果最好，肖维勒准则处理效果较差。

图5 4，13参数输入的叶绿素a含量预测效果Fig.5 Comparison of Chlorophyll-a content prediction results with 4 and 13 input parameters

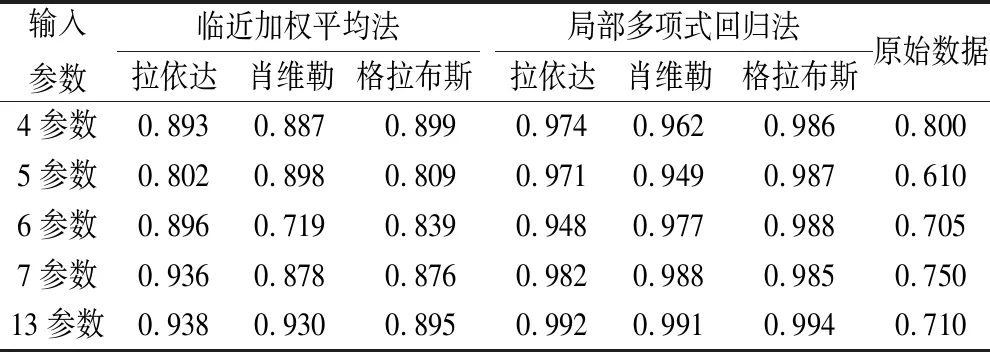
表3 不同数据处理方案的预测精度Tab.3 Prediction accuracy of different data processing schemes

注：不同数据处理方案得到的主影响因素不同，相应不同方案的最优输入参数组合不同。

整体而言，采用局部多项式回归方法对数据进行平滑处理，对预测精度改善优于临近加权平均方法，如图7、8所示，采用局部多项式回归的叶绿素a含量预测误差，整体波动幅度更小。格拉布斯准则异值处理组合局部多项式回归法平滑数据，在不同输入参数数量下均可达到最佳预测结果。该方案可以将以叶绿素a、气温、光强及气压4项因素下的叶绿素a预测精度从原始数据的0.800提高至0.986，同比提高23.25%。

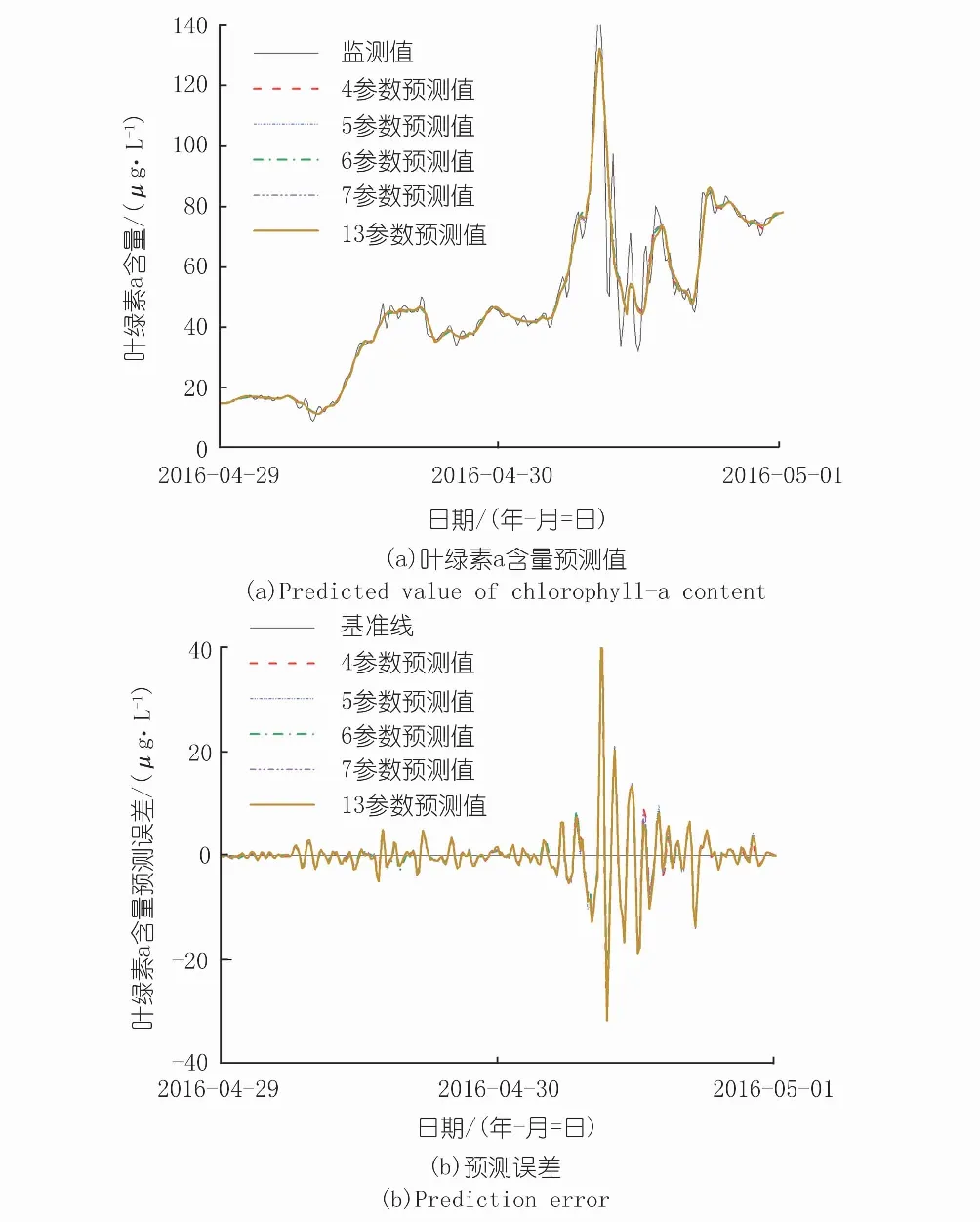
图6 原始数据的不同输入参数预测效果Fig.6 Different input parameters′ prediction effects with initial data

图7 临近加权平均法的叶绿素a含量预测效果Fig.7 Prediction effect of chlorophyll-a content by weighted average method

图8 局部多项式回归法的叶绿素a含量预测效果Fig.8 Prediction effect of chlorophyll-a content by local polynomial regression method

4 结 论

本文对神经网络的训练数据进行预处理，建立了35种组合方案，对基于BP神经网络叶绿素a含量平均生长率进行预测，对比分析预测结果，评估数据处理对基于神经网络的叶绿素a预测精度的影响。得到如下结论。

(1) 主成分分析方法可为BP神经网络输入参数选择和简化提供极为重要的参考。

(2) 利用数据处理技术对基础监测数据进行处理，可显著提高基于神经网络的叶绿素a含量预测精度。

(3) 不同的数据处理方案对基于神经网络的叶绿素a预测精度影响幅度不同；以格拉布斯准则进行异值处理，组合局部多项式回归法进行数据平滑，是本研究的最佳数据处理方案。

(4) 本研究方法的内在作用机理，需要在对数据处理前后幅值、频谱等数据特征变化进行深入研究后明确。