土壤中硝态氮迁移转化的数值模拟研究

(中国地质大学(武汉) 环境学院，湖北 武汉 430074)

近年来农业生产中氮肥的施用量大大增加，氮素在土壤中的存在形态可以分为有机氮、硝态氮、铵态氮和亚硝态氮[1]。由于硝态氮不易被土壤胶体吸附[2]，易随降雨和灌溉水从土壤表层向土壤深层迁移，进而淋失到地下水中，造成地下水污染。所以，深入研究硝态氮在土壤中的淋失过程，对合理施用氮肥和控制地下水污染均有重要意义。

在影响硝态氮淋失的众多因素中，灌溉量和施氮量是极其重要的两个因素[3]。研究土壤中硝态氮的方法主要为田间试验和土柱试验。鲁艳红[4]以两系杂交稻为研究对象，研究了不同施氮量对水稻产量形成及产量构成因子的影响，分析了不同施氮水平下氮素吸收利用效率的差异。冯绍元[5]通过在北京顺义区进行模拟降雨的田间试验，研究了不同降雨与施肥水平对玉米土壤硝态氮分布与累积的影响。张海涛[6]通过开展室内土柱实验研究了碳源对潜流带中氮素迁移转化的影响。随着计算机技术的发展，现阶段对硝态氮的研究已优化为田间试验、室内试验与数值模拟相结合的方法。何佳吉[7]通过对宜兴市梅林流域土壤中水分运动以及硝态氮淋滤过程进行动态模拟分析，揭示了氮肥施用与硝态氮淋失之间的关系。Arash Tafteh[8]通过数值模拟，分析评价了施用不同氮肥对土壤中硝酸盐的浸出率和变化量的影响。Li[9]则运用试验与数值模拟相结合的方法研究了农田地表径流中硝态氮的淋失规律。

洞庭湖地区是我国重要的粮油生产和养殖业生产基地，常德市位于洞庭湖西部，独特的气候和丰富的水土资源极利于农作物的生长，该地区粮食、棉花总产值居湖南之首。然而由于该地区长期施用大量氮肥，有些未被植物吸收利用的氮肥经土壤入渗到含水层中造成地下水污染。本文以常德市典型浅层土壤为研究对象，通过室内静态试验和动态土柱淋滤试验获得硝态氮静态条件和淋滤条件下的迁移转化规律及相关参数。在此基础上，利用数值模拟软件建立数值模型，并通过校正好的模型模拟不同灌溉强度下硝态氮浓度的变化特征，探讨分析灌溉强度对硝态氮浓度的影响，从而为该地区氮肥施用和地下水保护提供科学依据。

1 物理试验模型

1.1 土柱试验装置及试验方法步骤

1.1.1试验装置

土柱淋滤装置由用于稳定水头的马氏瓶、土柱和取样瓶组成。土柱主体为有机玻璃柱，内径 8 cm，高度50 cm，侧壁36 cm和48 cm 深度处设有取样口。实验装置简图如图1所示。

1.1.2土样性质及装填

本次试验土样采集于常德市辰阳村 0～20 cm 耕作层，土样采集后经自然风干过2 mm筛，按《土壤农化分析》测定土样基本理化性质。经测定，土样基本理化性质如下所示。

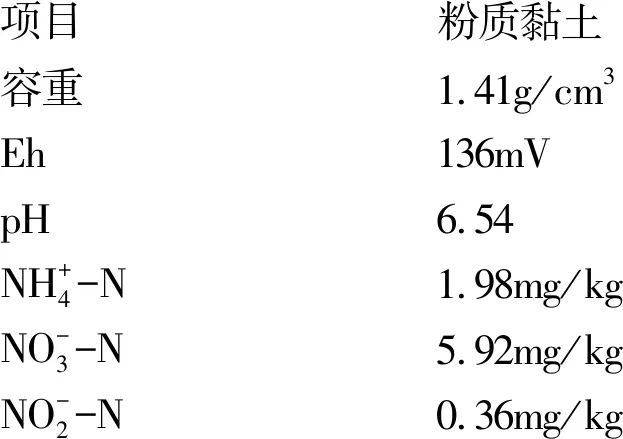
项目粉质黏土容重1.41g/cm3Eh136mVpH6.54NH+4-N1.98mg/kgNO-3-N5.92mg/kgNO-2-N0.36mg/kg

装填土样时先在柱子底部装入2 cm 厚的石英砂防止土壤冲散堵塞出水口；之后将风干的土样按实测容重换算称重后装入柱内，隔1 cm分层装填，使土样尽量压实均匀；最后再在土柱的顶部装入2 cm厚的石英砂，防止淋滤液进入土柱时冲散土壤，使之均匀进水。

1.1.3淋滤液的配置

根据湖南省统计年鉴，2015年湖南省年降雨量为1 580.50 mm，占30%循环地表径流；耕地面积415.35万hm2，全省氮肥使用量为2 016 259 t。为便于计算，配置40 mg/L 的硝酸钠溶液(以N计)进行淋滤。

1.1.4淋滤试验及取样分析

首先从土柱底部注入去离子水，排除土柱内空气。当土柱顶部有水溢出时，改从土柱顶部进水。然后通过控制装置使土柱中流场保持稳定，改换配置好的淋滤液进行淋滤。

由于土样渗透系数较小，每隔3 d从取样口取样，测定铵态氮、亚硝态氮、硝态氮含量。

采用纳氏试剂分光光度法检测铵态氮，采用α-萘胺光度法检测亚硝态氮，采用紫外分光光度法检测硝态氮。

1.2 土柱试验结果

图2 硝态氮浓度随时间变化曲线Fig.2 The temporal variation of concentrations at different soil depths

2 数学模型

2.1 水流运动基本方程

在不考虑土壤水平和侧向水流运动时，即在一维垂向运移中，水流运动可以用 Richards 方程来描述[10-11]，方程如下：

(1)

式中，θ为土壤体积含水率；h为土壤压力水头；t为模拟时间；α为流向与垂直向夹角，根据上述物理试验模型，其水流为一维垂向渗流，即α=0；K为非饱和渗透系数；S为源汇项。

2.2 水分运移方程

土壤水分运移模型可用来描述水分在土壤中的运移过程。HYDRUS-1D 软件水流模型中包括单孔介质模型、双孔隙/双渗透介质模型等多种土壤水分运移模型。本文模拟时采用 Van Genuchten-Mualem 提出的土壤水力模型来进行模拟预测，且在模拟中不考虑水流滞后的现象[12]，方程为

(2)

K(h)=KsSel[1-(1-Se1/m)n]2

(3)

(4)

(5)

式中，θr为土壤残余含水率；θs为土壤饱和含水率；Se为有效饱和度；α为冒泡压力；n为土壤孔隙大小分配指数；Ks为饱和水力传导系数；l为土壤孔隙连通性参数，通常取0.5。

2.2 溶质运移方程

土壤溶质运移主要有3个过程，分别为对流、分子扩散和机械弥散。本文模拟时采用经典的对流-弥散方程描述饱和-非饱和孔隙介质中的一维溶质运移[13]。

(6)

式中，c为溶液液相浓度;ρ为土壤容重;s为溶质固相浓度；D为综合弥散系数；q为体积流动通量密度；S为源汇项。

3 数值模拟

3.1 网格剖分和时间步长

根据土柱淋滤试验，模拟时将模拟土柱均等化分，进行1 cm等距剖分，并在36 cm和48 cm设置观测点。初始时间步长设为0.001 d，最小时间步长设为0.001 d，最大时间步长设为0.1 d，迭代控制参数则使用默认值。

3.2 初始条件与边界条件

由于氮的转化过程十分复杂，本文建立模型时只考虑铵态氮、亚硝态氮和硝态氮之间的转化。进行土柱淋滤试验时采用马氏瓶从土柱上端连续进水保持进水压力水头不变，因此水流模型上边界选用恒定压力水头边界(Constant Pressure Head)，水流模型的下边界概化为包气带底部(即潜水面)，所以下边界选用自由排水边界(Free Drainage)；土柱试验采用40 mg/L 的硝酸钠持续淋滤，所以溶质运移模型的上边界设定为恒定浓度边界(Constant Concentration Boundary Condition)，下边界设定为零浓度梯度边界(Zero Concentration Gradient Boundary)，代表初始状态为液相0浓度状态。设置初始水头时，软件根据介质剖分的节点数对初始水头进行离散。将模型顶部的压力水头设为0 cm，表示初始时刻土壤表层处于近饱和状态，而土柱底部的压力水头设为-48 cm，初始压力水头自上而下为0～-48 cm 均匀分布。

3.3 参数确定

数值模拟溶质运移的主要参数包含土壤水力特征参数、溶质运移特征参数和溶质反应特征参数[14]。

3.3.1土壤水力特征参数确定

将过2 mm筛的风干土样采用马尔文激光仪进行粒度分析试验，试验结果显示该土样黏粒(0.01～2.00 μm)所占百分比为3.60%，粉粒(2.00～50.00 μm)所占百分比为96.4%。利用模拟软件水流运动参数界面中的神经网络预测功能(Neural Network Prediction )，根据土壤质地和容重来进行监测 VG 型水分曲线的水力学参数的预测。输入土壤砂粒、粉粒及黏粒的百分比组成及土壤容重，即可以得出曲线中所需要的参数。输入数据并根据模拟结果调整参数得出土样各水力特征参数如表2所示。

表1 土壤水力特征参数Tab.1 The hydraulic characteristic parameters of the soil

3.3.2反硝化反应速率测定

表2 反硝化反应转化量及转化率Tab.2 Denitrification reaction conversion and conversion rate

由实验数据可知，0～1 d时的反硝化作用较为微弱，反硝化作用对于硝酸氮浓度的影响主要发生在1～4 d，4 d后反硝化反应速率缓慢，所以以 1～4 d的硝酸氮浓度变化曲线计算反硝化动力学方程。经过拟合发现，1～4 d反硝化反应符合一级反应速率方程，速率常数为 0.399，硝态氮浓度呈指数形式下降。

图3 硝态氮浓度随时间变化曲线Fig.3 The temporal changes of concentrations at different time

表3 氮素迁移转化参数Tab.3 N transport and transformation parameters for the soil profile

3.4 模型校正及检验

输入土壤性质参数验证模型的可靠性，以土柱不同深度观测点的硝态氮含量实测值及其淋滤液浓度为模型的初始边界条件，模拟计算硝态氮的变化情况。将实测硝态氮的浓度与模拟值进行对比，图4 是硝态氮模拟值与实测值随时间变化的比较结果。由图可知：对土柱 2 个深度处的观测点进行取样监测，测得土壤溶液中硝态氮浓度模拟曲线与实测曲线变化形态基本一致，模拟值与实测值相差不大。1～4 d模拟 48 cm 处的硝态氮浓度拟合要优于 36 cm 处，这主要是因为硝化作用主要发生于 1～4 d，由于土柱底部与外界空气相连通，48 cm 处较 36 cm 溶解氧多，抑制了反硝化作用。而模拟时则认为模型各点反硝化反应均为一级反应且反应常数相同，输入模型的静态反硝化反应速率常数测定环境更近似于 48 cm 土柱处的环境，所以 1～4 d土柱 36 cm 处硝态氮浓度模拟值高于实测值。而在试验第 10 天 48cm 处实测土壤硝态氮含量有明显升高，与模拟值偏离较大，这可能是因为取样点变化造成的土壤背景值差异所导致。通过 SPSS软件进行模拟值与实测值的距离相关分析(以 Pearson 相关系数为距离)，36 cm 和48 cm 硝态氮含量实测值与模拟值相关系数分别为 0.998 和 0.995 ，皆达到显著水平，说明模拟效果较为理想，模型可以较好反映硝态氮在土壤水中的运移情况。

图4 实测硝态氮的浓度与模拟值对比曲线Fig. 4 Comparison of the measured and

4 不同灌溉强度硝态氮浓度的变化特征

常德市虽然雨量充沛，但降雨较集中，缺水季节需要对农作物进行灌溉。利用校正后的模型对不同灌溉强度下硝态氮浓度变化进行模拟。该地区土壤渗透系数约为 4 cm/d，将灌溉强度分别设为1，2，4，8，12 cm/d，运行模型。模拟结果如图 5 所示。

图5 不同灌溉强度硝态氮浓度Fig.5 The values of concentrations in different irrigation intensity scenarios

各组灌溉强度下硝态氮的浓度最大值相差不大，硝态氮浓度总体变化为先升高后降低。不同灌溉强度影响入渗到土壤中的水量，引起土壤剖面含水率变化，进而影响土壤硝态氮浓度变化。当灌溉强度大于 4 cm/d 时，超过土壤的下渗能力，灌溉水按下渗能力下渗，多余的水会形成地面积水，进而形成地表径流，所以模拟 10 d后各组土柱底部硝态氮的浓度差异不大；当灌溉强度小于等于4 cm/d 时，灌溉水全部下渗到土壤中，而硝态氮易溶于水中，所以模拟10 d后土壤中硝态氮浓度随灌溉强度的增加而增大。

5 结 论

土壤中硝态氮的静态反硝化作用主要发生于实验开始后 1～4 d，在这期间硝态氮浓度呈指数形式下降，反硝化反应近似一级反应，反应速率常数为0.399/d，试验4 d后反硝化速率缓慢，反硝化作用对硝态氮浓度影响比较微弱。由于硝态氮易溶于水中，易随灌溉水下渗到土壤中，而灌溉水的入渗量受土壤下渗能力制约：当灌溉强度大于土壤下渗能力时，灌溉水按下渗能力下渗，多余的水会形成地面积水，进而形成地表径流，硝态氮浓度的变化趋势基本一致；当灌溉强度小于等于土壤下渗能力时，灌溉水全部下渗到土壤中，硝态氮浓度随灌溉强度的增加而增大。通过控制灌溉强度，使其约为 4 cm/d，既可以提高水的利用，也可以减少硝态氮向土壤深层大量流失，控制硝态氮污染土壤和地下水。