基于潜变量模型的多元有序数据轮廓分析法
2019-05-11孙丰霖鲁统宇类淑河
孙丰霖,鲁统宇,类淑河
(1.中国海洋大学 a.海洋与大气学院;b.数学科学学院,山东 青岛 266100;2.中国计量大学 经济与管理学院,浙江 杭州 310018)
一、引言
定量数据和定性数据是数据的两种基本类型。前者包括取值连续的计量数据和取值为整数的计数数据;后者包括无序的名义数据(Nominal Data)和有顺序概念的有序数据(Ordinal Data)[1],名义数据和有序数据产生于名义变量和有序变量。“有序”是指按照一定的顺序对变量进行分类,不同类别之间的距离并不需要相等的一种测量尺度。在处理有序数据时,以一种定量的方式进行赋值在数据处理中十分有益[2]。虽然可以对有序数据进行人为的赋值1,2,…,但不能假定这些类别之间的差距是一致的[3]。如果简单地将其看作等距,得到的结果往往不准确甚至完全错误。因此,用于计量数据的模型和方法一般不能直接推广到有序数据上。国内外已经有一些学者研究有序变量在模型中的赋值问题[4-6]。对于有序数据,一般不能直接计算均值、方差等统计量,但如果能够将其客观合理地赋值,令该值能够代表该类别的“数量”关系,那么应用于连续数据的方法就可以应用到有序数据上来。所以,一种合理的赋值方法对有序数据分析而言尤为重要。
多总体位置参数比较问题在实际数据分析中十分常见。对于正态数据而言,常用方法是方差分析,当数据不满足正态性和方差齐性时,方差分析就不再稳健[7]。对于连续型非正态数据,有一些学者研究适用于这类数据的方差分析方法[8]。除此以外,还存在许多非参数方法,例如Brown-Mood中位数检验和Wilcoxon-Mann-Whitney秩和检验,不过后者仅仅适用于两样本总体分布函数形状相似,只在位置上有所不同的情况(如平移),样本量、偏度、方差会对这种检验的稳健性有较大的影响[9]。多总体的Kruskal-Wallis秩和检验、Jonkheere-Terpstra检验和Friedman秩和检验也有取值连续的假定,相比较于方差分析,即使正态性成立,Friedman秩和检验也能够保证安全和合理的渐进相对效率,是一种十分稳健的非参数方法。对于非连续的数据,二元响应Cochran检验仅适用于取值为1或0的定性数据,研究多个一元总体的位置参数是否一致的问题[10]。
除了Cochran检验,上述方法都适用于连续数据。由于有序数据的不连续性和打结现象(数据中存在相同的数字),前面的方法都不够稳健甚至无法使用,这就对新的检验方法提出了要求。如果假定有序变量是潜变量的粗略度量,那么某些参数方法就可以适用于这类变量,Lu等提出了针对有序数据的多重比较方法,通过正态潜变量模型解决有序数据的一元多总体期望是否一致的问题,该方法假定观测到的有序数据是对某一潜在的连续正态变量的一种粗略度量,通过对潜变量总体均值的两两比较来得出结果[11]。在此基础上,一元有序数据的多组别问题可通过方差分析的方法解决。事实上,这些方法都是针对一元数据而言的。对于多元数据,由于缺少秩的概念,多数非参数方法无法使用。但在社会调查等领域中,经常会遇到有序数据的多元多组别比较问题。这时,各元之间往往不是相互独立的,而会存在一定相关性,再加上数据不连续性,使得这个问题更加难以解决。轮廓分析可以解决多总体均值向量的比较问题。近十几年来,有不少轮廓分析的研究成果出现[12-14]。不过,这些成果都是针对连续型数据而言。目前,国内外还没有将轮廓分析应用到有序数据的研究成果。
本文介绍了采用潜变量模型对有序数据进行赋值,利用轮廓分析解决多元有序数据的多个总体均值向量的比较问题。当有序变量看作潜变量的粗略度量时,可根据样本频率计算各个区间的临界值,将各个区间的积分平均值作为有序变量各类别的代表值。此时,均值、方差等统计量就可以进行计算。轮廓分析要求数据满足多元正态性。为了使非连续非正态的有序数据变为连续正态的数据,本文采用Bootstrap方法重构数据。这个过程将原始数据中有关总体均值的信息保留到重构数据中,二者有着相同的总体均值,对重构数据总体均值的轮廓分析也就是对原始数据总体均值的轮廓分析。轮廓分析包括单总体、两总体和多总体三种情形,本文介绍了各情形下的假设检验方法,给出相应的检验统计量和拒绝域。
通过随机模拟验证本文模型方法的合理性。首先对重构数据进行多元正态性检验。然后,以单总体和两总体情形下的平行假设为例,检验该方法在控制两类错误上的能力,得到结论:当原始样本均值、协方差阵等与总体一致时,该方法在控制假设检验第一类错误上有很好的效果且保证了较好的检验功效;而在一般情况下,该方法的实际第一类错误(简称“实际error I”)较于名义第一类错误(简称“名义error I”)发生一定程度的“膨胀”现象。不过,该问题可以通过增大原始样本量、降低名义error I和进行多次试验来解决。文章最后对方法的适用范围和未来的研究方向进行了讨论。
二、方法
(一)潜变量模型
对于有序变量z,假定存在一个潜在的连续变量x,代表z在各类别下潜在的真实值。通常假设x的取值范围是从-∞到+∞,潜变量x可以用于有连续性要求的统计方法和模型。若z有m个类别,记为1,2,…,m,则z和x的对应关系是:
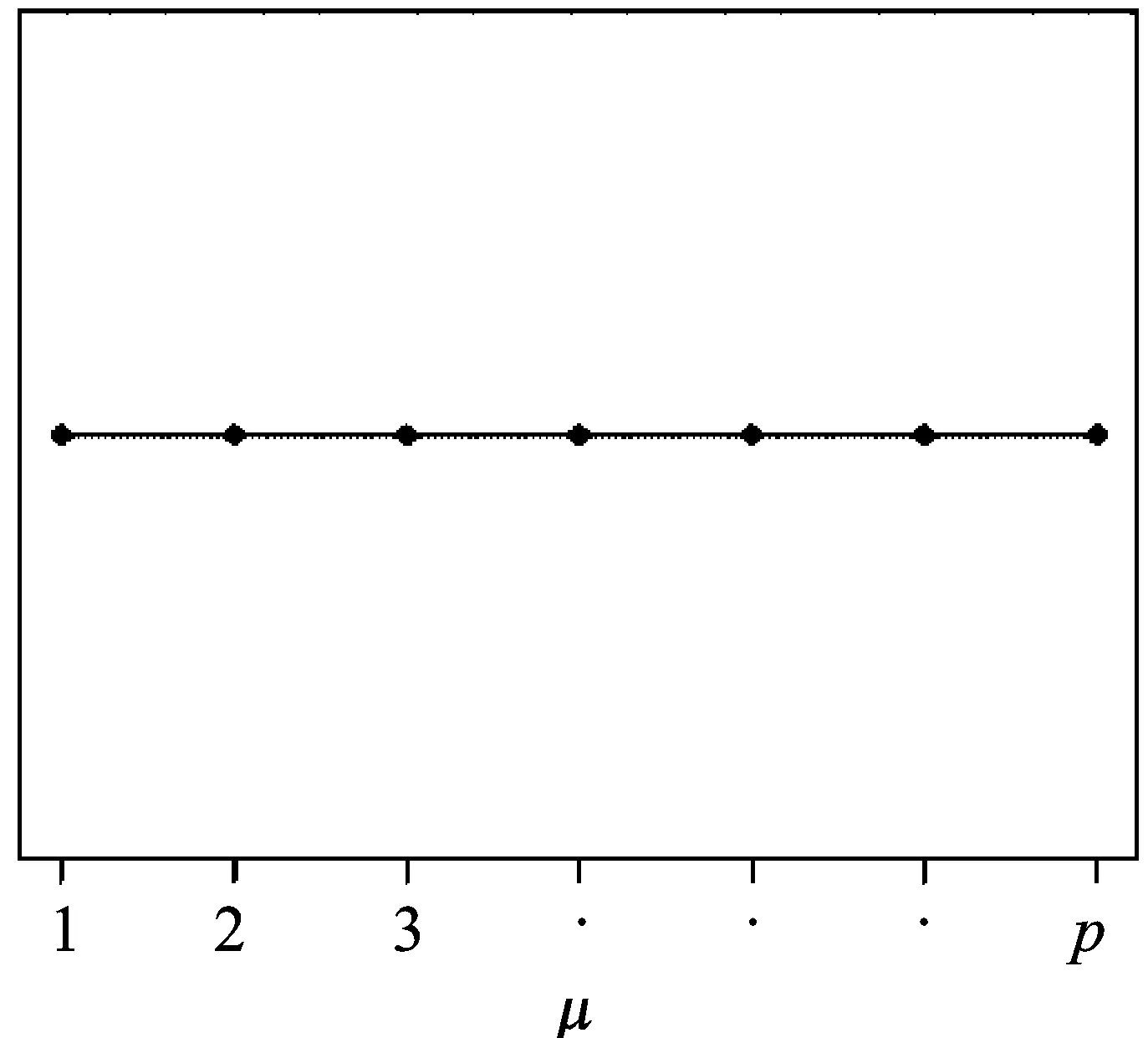
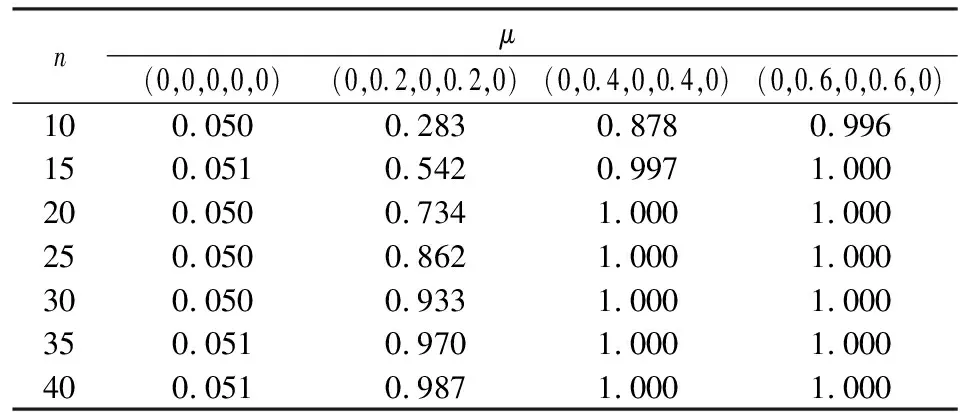
z=i⟺τi-1 pi=Pr[z=i]=Pr[τi-1≤x<τi] =Φ(τi)-Φ(τi-1) 各个类别的临界值确定后,可以通过计算积分平均值的方法得到各类别的代表值,即: 这样就解决了有序变量z的赋值问题,接下来就可以将ai作为各类别的真实代表值来计算均值、方差等统计量。陈民恳所介绍的秩方法也可以视为一种潜变量方法,该方法假设潜变量服从固定区间上的均匀分布[16]。 对于多元有序数据,对每个变量按照潜变量模型中的方法进行赋值,赋值后的多元变量可以视为来自以下定义的离散分布,记ξ=(ξ1,ξ2,…,ξp)′是p维随机变量,其中ξi的概率分布为: ξiai1ai2…aiti pipi1pi2…piti 1.单总体情形 以总体G1为例,通过样本阵X1来检验μ1=(μ11,μ12,…,μ1p)′中的各个分量μ11,μ12,…,μ1p是否在同一水平上(见图1),即: H0:μ11=μ12=…=μ1pH1:μ1i≠μ1j∃i,j 图1 单总体同水平假设图 记(p-1)×p维矩阵 2.两总体情形 以总体G1,G2为例,通过样本阵X1,X2来检验μ1,μ2的两条轮廓线是否平行(见图2),是否同水平(见图3)和是否平坦(见图4),即: 图2 两总体平行假设图 图3 两总体同水平假设图 图4 两总体平坦性假设图 (1)平行假设 (2)同水平假设 (3)平坦性假设 多样本问题类似于两样本问题,对于总体G1,G2,…,Gk,通过样本阵X1,X2,…,Xk来检验k条轮廓线是否平行,是否同水平和是否平坦。 1.平行假设 2.同水平假设 3.平坦性检验 为了简化过程,本节省略赋值过程,只对赋值后的数据进行随机模拟,即直接随机生成各元服从给定离散分布的数据。以维数p=5为例,随机变量ξ=(ξ1,ξ2,ξ3,ξ4,ξ5)的均值向量μ=(0,0,0,0,0),从ξ中生成随机样本,选择不同的自助样本容量m和自助样本数量n进行重构数据,对重构数据进行多元正态性检验(每个m和n组合进行105次试验),结果见表1。 表1 多元正态假设拒绝率(α=0.05) 从表1可以看出,固定n时,随着m的增大,正态拒绝率均逐渐减小,这与中心极限定理的渐进正态性相吻合。当m<25,n不大时,正态拒绝率十分低,而随着n增大,正态拒绝率急剧上升。在m=25时,拒绝率随n的提高上升比较缓慢,且不高于给定的α=0.05。结论:重构数据至少使得自助样本容量m达到25,才能有效地保证数据的正态性。 首先考虑样本质量十分高的情况,即样本是总体的很好代表,样本均值、样本协方差阵与总体期望、总体协方差阵基本相同。以均值向量μ是锯齿形的5维随机变量为例进行模拟。定义轮廓线的极差:锯齿的高峰与低谷之间的最大差距。按照不同的极差,分别进行同水平的轮廓分析,计算同水平假设的拒绝率(每个组合进行105次试验),结果见表2。 从模拟结果来看,当同水平原假设成立的时候(表2第1列),无论n取何值,实际error I基本在0.05左右徘徊,这个结果符合假设检验中α=0.05的含义:在原假设成立的情况下,有5%的概率拒绝原假设,所以该方法可以有效地控制第一类错误。对于不满足原假设的总体(表2第2~4列),检验的通过率会随着极差的增大而降低,即使对于极差较小的第2列,假设检验结果也会随着n的提高更加准确,所以检验的功效会随着极差和n增大而提高。此外,不同的原始样本量s并不会对上述结果产生影响。所以,对单样本情形,从第一类错误和检验的功效来看,此方法在样本质量较高时有很好的效果。 表2 单样本同水平假设拒绝率(α=0.05,m=25) 不过在实际中样本质量往往是未知的,此时样本均值、样本协方差等与总体可能存在一定差异。于是按照给定的原始样本数量s=100,200,…,500,先随机抽样得到原始样本(这些原始样本与表2的样本不同之处在于,由于随机性,前者的样本均值、样本协方差阵不一定与总体相同),再从原始样本中按照n=10,15,…,40进行重构样本,以均值向量μ=(0,0,0,0,0)为例,检验该方法对同水平假设的拒绝率,即实际error I,每个组合进行105次试验,结果见表3。 表3 单样本同水平假设拒绝率(m=25) 从表3中可以看出,对于不同的s和n的组合,该方法的实际error I会发生不同程度的“膨胀”现象,根本原因在于该方法是基于原始样本进行的重抽样,随着n的增加,自助样本的均值会偏向原始样本的均值而不是总体均值,这一点也会随着n的增加而更加明显。如果原始样本均值与原总体有一定差异的话,那么对自助样本的检验会倾向于拒绝原假设,这样会导致实际error I增加。此外,实际error I会随s增大而减小且越来越接近α。对于发生的“膨胀”现象,本文给出3种解决方法: (1)增大样本量s。随着样本量s的增大,样本会越来越能代表总体,与总体的差距会越来越小,也就越来越趋近表2的情况,此时error I和error II都会得到有效控制。 (2)适当降低名义error I-α。虽然当α=0.05时,没有组合的实际error I达到0.05,但当α调低至0.01时,有很多情况可以使实际error I达到0.05。 (3)多次进行试验。由于该方法是以重构样本为基础的检验方法,所以能够进行多次抽样和假设检验。例如,当α=0.05,s=200,n=20时实际error I为0.216,制定策略:进行7次试验,当有4次或4次以上拒绝时才拒绝原假设,此时的实际error I就会降低为0.043<0.05。能够多次进行试验是该方法最大的优势所在。 在控制error I方面,一般不会采取降低n的方式,因为随着n的降低的确可以使实际error I减低,但这样也会使实际error II提高,令检验功效降低。在实际中,由于客观因素的限制,原始样本量可能不能任意增加,所以比较合适的方法是降低名义error I和进行多次抽样试验两者配合使用。 与单样本类似,对两样本平行假设也按照样本质量分两种情况进行随机模拟,样本质量较高时,对总体平行和不平行两种情况进行模拟。在平行情况下,两个均值向量的轮廓线为锯齿形,并定义两条轮廓线的差距是两条线通过平移达到重合所经过的最小距离。在不同的极差和差距下,探究随着n增大,对原假设的拒绝率的变化,结果见表4。 表4 两样本平行假设拒绝率(α=0.05,m=25) 从表4中可以看出:无论是轮廓线的极差r和差距l,还是自助样本数量n都不会影响该方法的实际error I,随着n的增加也能保证较好的检验功效。同样原始样本量s也不会产生显著影响。所以,在样本质量较高的情况下,对两样本平行假设,该方法有很好的效果。针对一般样本情况,实际error I见表5,结论与单样本情形类似:该方法也会产生一定的实际error I的“膨胀”现象,同样可以通过增大原始样本数量、降低名义error I和进行多次试验来解决。 表5 两样本平行假设拒绝率(m=25) 对于两样本的其他检验和多样本检验,通过随机模拟可以得到类似于平行假设的结论。 本文的方法实际上是将原始样本作为一个新的总体,通过对新总体的重构样本进行检验来得出结论。在这个过程中,合适的自助样本容量m保证了重构数据的正态性,合适的自助样本数量n和名义第一类错误α保证了假设检验结论的正确性,减少误判的发生。由于Bootstrap方法重构数据的过程是可放回的随机抽样,原则上该方法对原始样本数量并没有要求。采用这种重抽样的方法能够让不连续的原始样本数据从离散分布转换为服从多元正态分布的重构数据,且在这一转换过程中保证了原始样本和重构样本拥有相同的总体均值。 从随机模拟的结果看,当样本能够很好地代表总体时,即样本均值和协方差阵偏离总体均值和协方差阵较少,即使是小样本也能够产生很好的效果。不过这在实际中一般是无法保证的,所以,大样本应该是更适合的应用范围。事实上,针对该方法可能会出现实际error I膨胀现象,可以通过增大样本量s、适当减小α和多次进行试验来解决这个问题,灵活调整试验的次数恰恰是Bootstrap重抽样方法所带来的优势之一。 本文随机模拟结果仅仅考虑了维数为5的情况,而更高维的数据会对该方法产生怎样的影响和小样本情况下如何对该方法进行改进还有待进一步研究。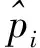
(二)重构数据和轮廓分析
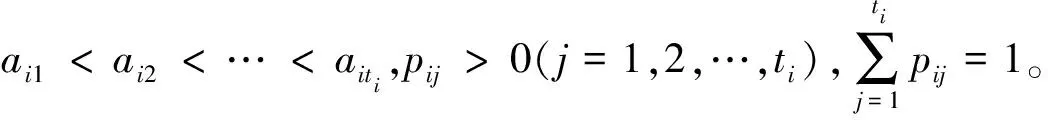
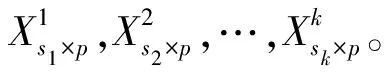
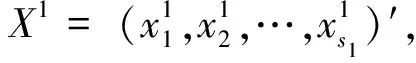

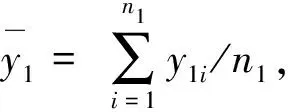
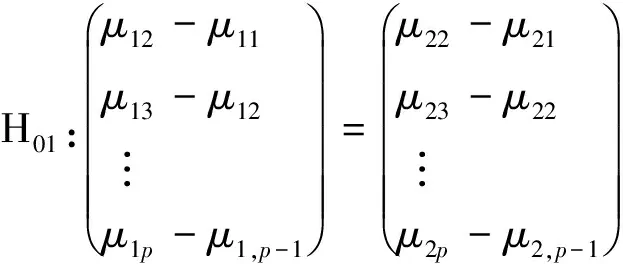
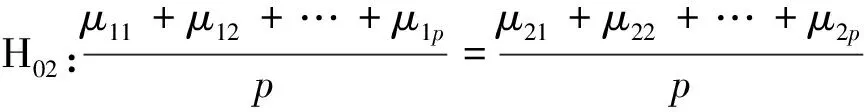
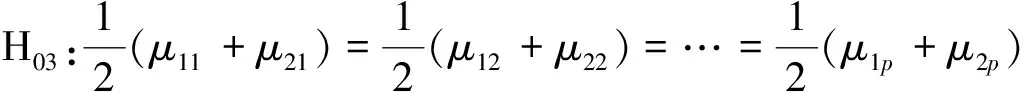
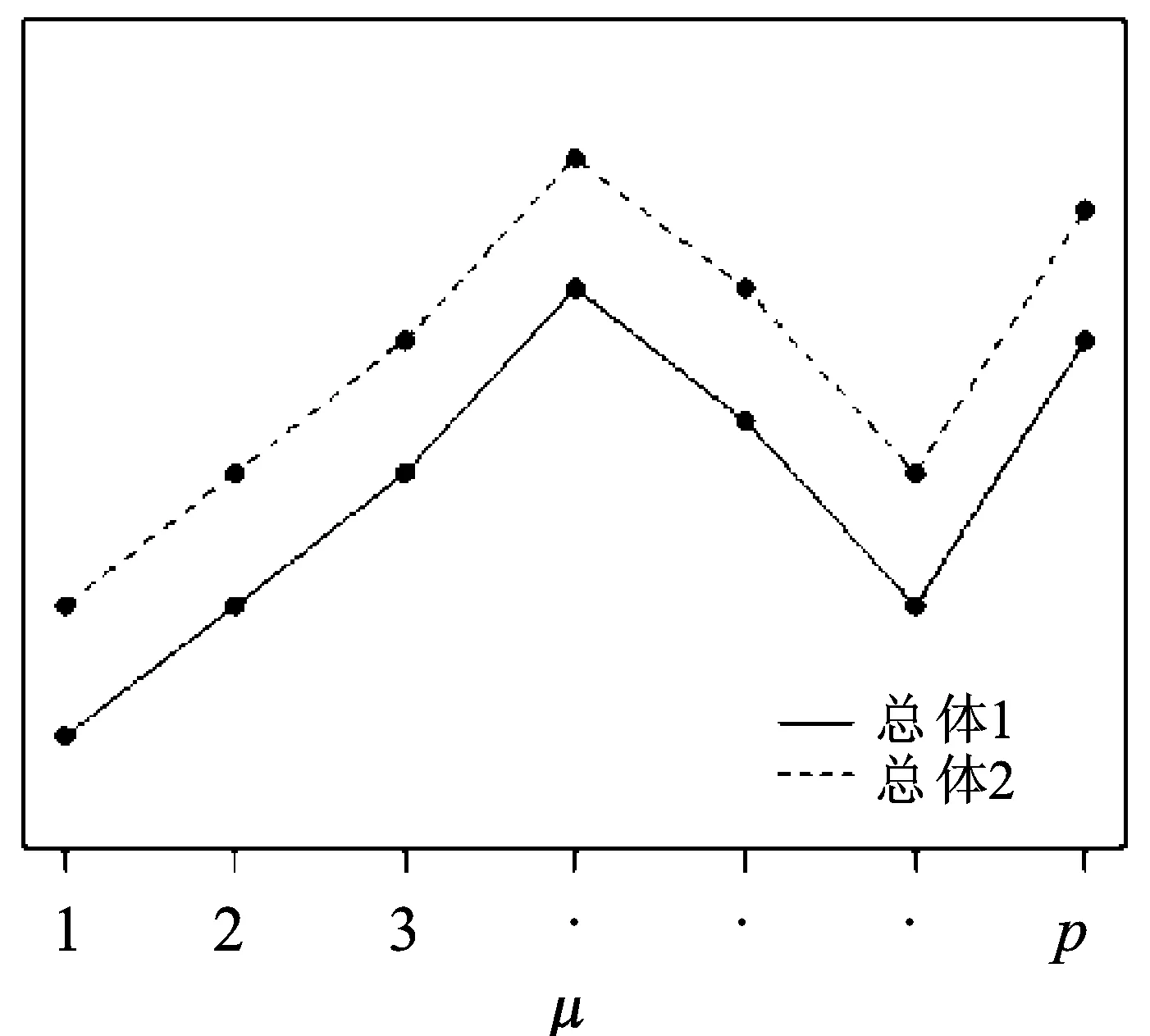
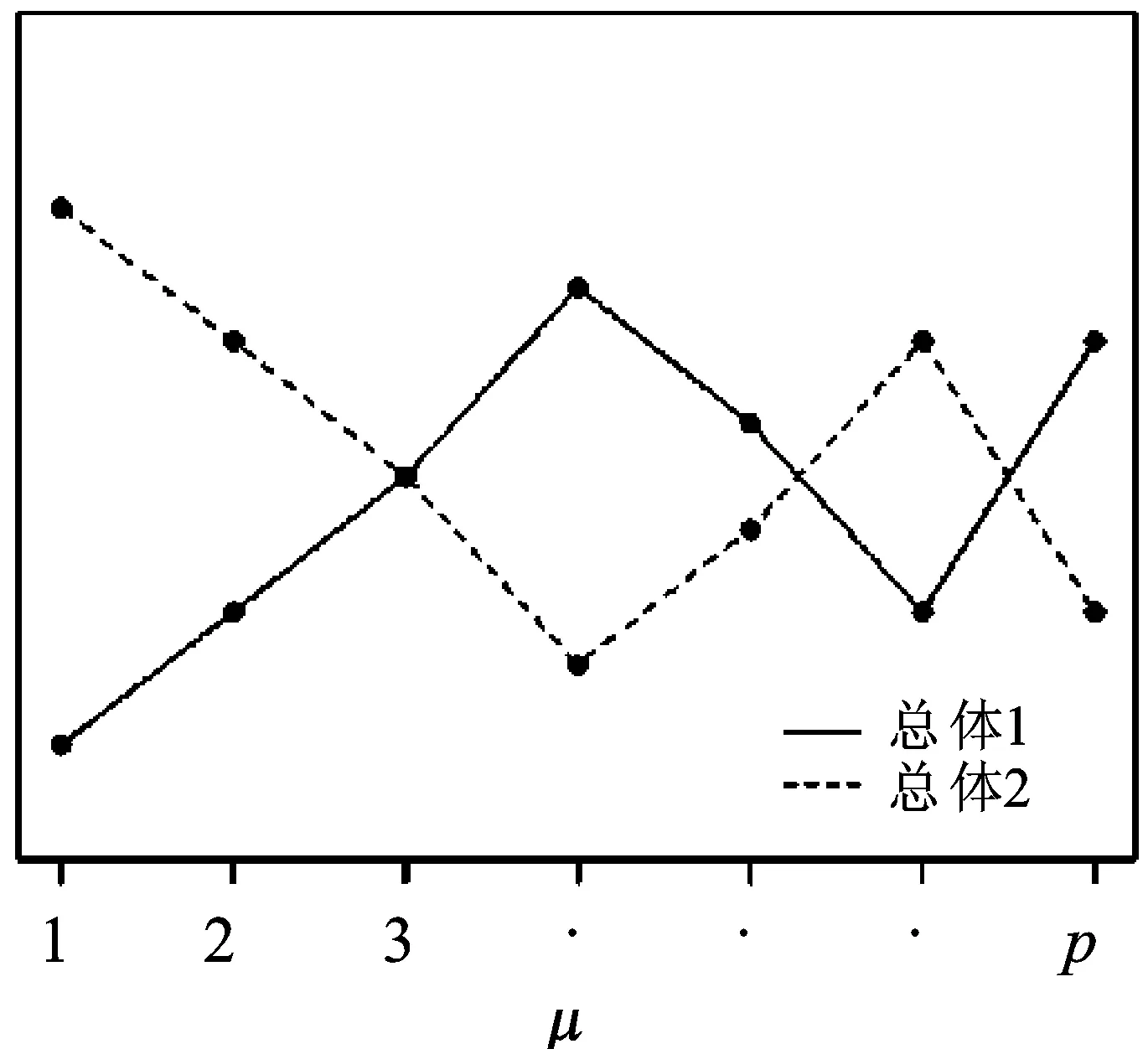
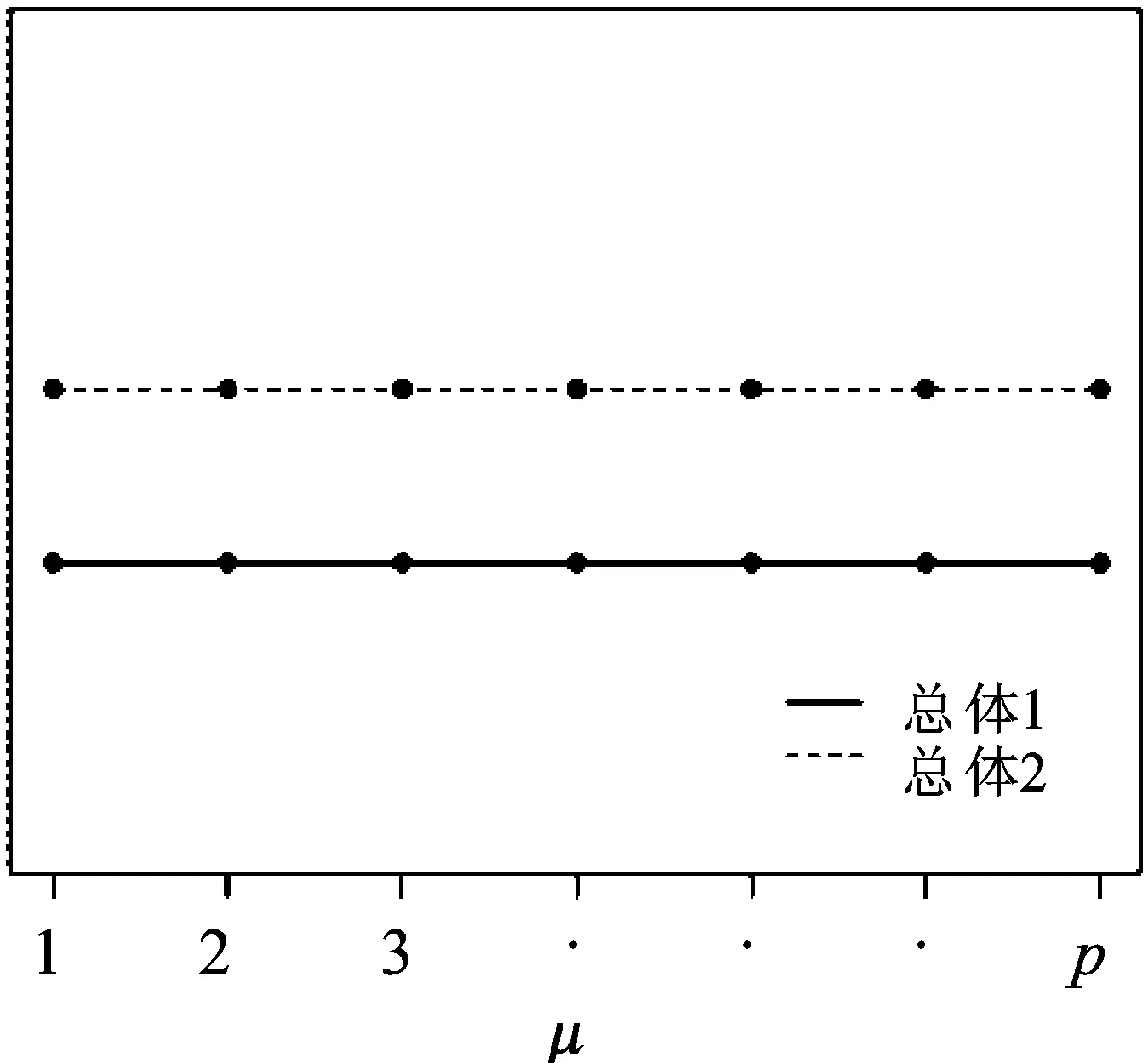
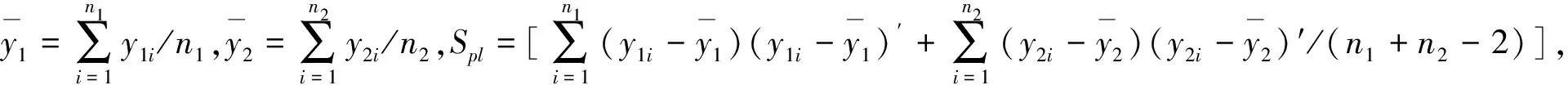
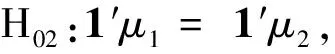
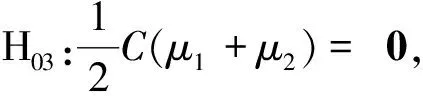
(三)多总体情形
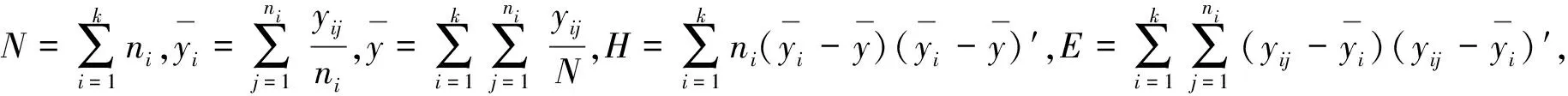
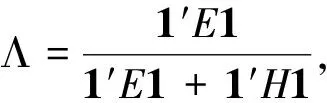
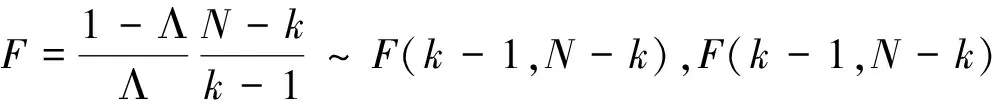
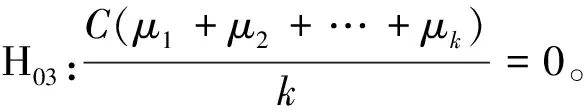
三、随机模拟
(一)正态性检验
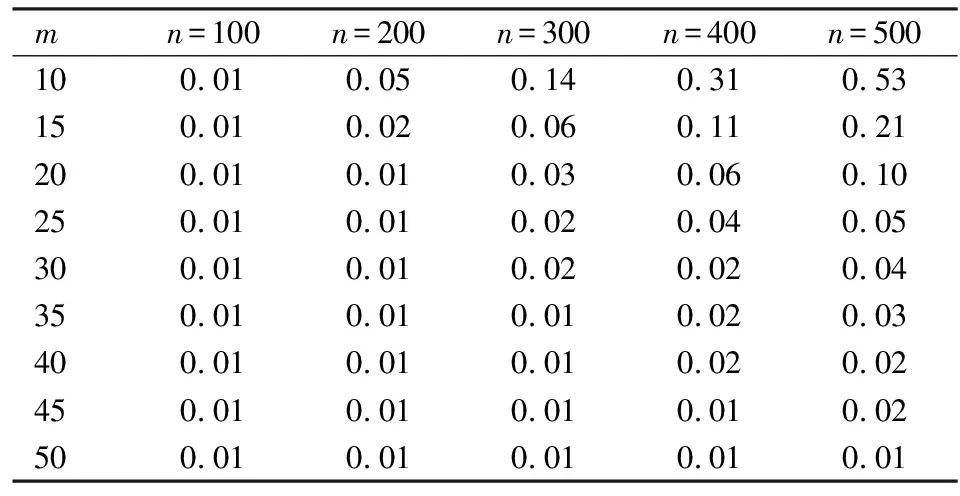
(二)单样本同水平检验
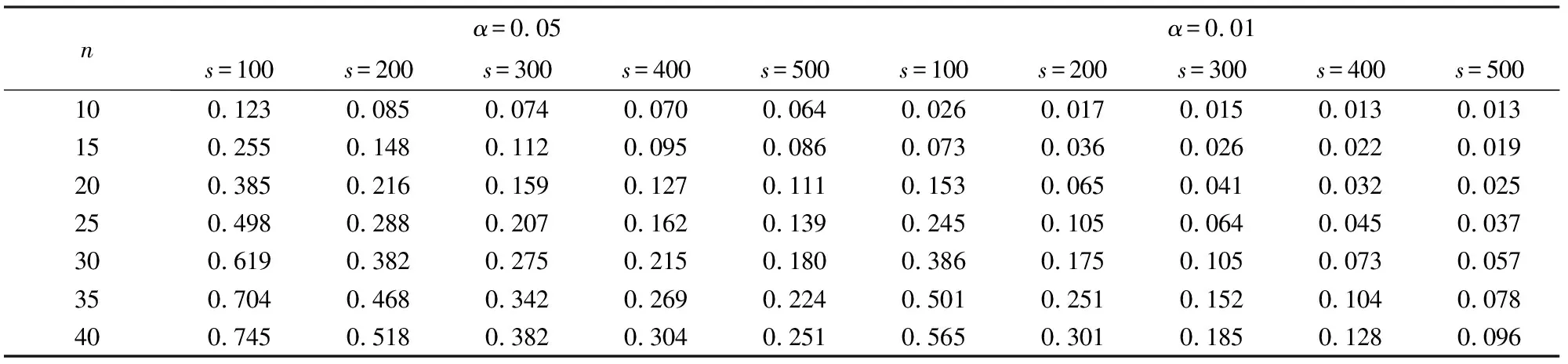
(三)两样本平行检验

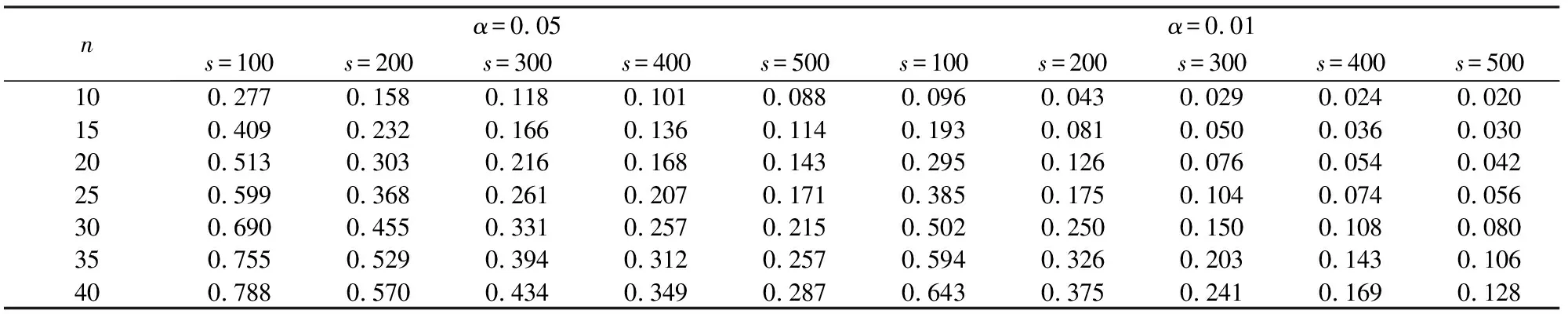
四、总结与展望
