EWT多尺度排列熵与GG聚类的轴承故障辨识方法*
2019-05-10赵荣珍李霁蒲邓林峰
赵荣珍, 李霁蒲, 邓林峰
(兰州理工大学机电工程学院 兰州,730050)
引 言
作为旋转机械设备的核心部件,滚动轴承的状态是否正常直接影响着机械设备的使用。统计发现,在旋转机械发生异常的原因当中,有30%是由轴承故障引起的[1]。因此,如何快速有效地对滚动轴承故障给予辨识,已经成为目前研究的一个重点。
对振动信号进行特征提取和故障识别是滚动轴承故障诊断研究领域关注的重要问题之一。源于滚动轴承的振动信号呈现出的非线性和非平稳性,使得传统的以傅里叶变换为基础的方法难以取得较好的分析效果[2]。Huang[3]提出的经验模态分解(empirical mode decomposition,简称EMD)是一种自适应信号处理方法,该方法不受不确定性原理的限制,非常适合非线性和非平稳信号的分析。但目前已发现这种算法仍存在着以下几个问题待解决:a.固有模态函数(intrinsic mode function, 简称IMF)的正交性无法通过理论证明;b.收敛条件不合理、过包络和欠包络等问题产生的模态混淆,易导致IMF阶数增加;c.计算过程需要多次迭代,得到一个实际的IMF分量需要较长时间等[4]。针对上述不足,Gilles[5]依据小波变换和窄带信号分析理论,提出了一种新的自适应信号处理方法——经验小波变换(empirical wavelet transform, 简称EWT),并把它成功应用于心电图信号(electrocardiogram,简称ECG)信号分离和图像降噪分析中。李志农等[3]不仅提出了基于EWT的机械故障诊断方法,而且将这种方法与传统的EMD方法进行的对比表明,EWT明显优于传统的EMD方法,这一结论还被后续的一系列研究所证实[6-9]。
排列熵是一种检测随机性和动力学突变的方法,它具有计算简单、抗噪能力强等特点[10]。Yan等[11]将排列熵引入到旋转机械振动信号特征提取中的结果表明,该特征能够有效地表征出滚动轴承在不同状态下的工况特征。类似于传统的单尺度非线性参数,排列熵仍可在单一尺度上描述时间序列的不规则性。Aziz等[12]还提出了多尺度排列熵(multi-scale permutation entropy,简称MPE)的概念,用于衡量时间序列在不同尺度下的复杂性和随机性,使鲁棒性得到加强。郑近德等[13]将多尺度排列熵概念运用在轴承故障诊断上,也取得了良好的诊断效果。
聚类分析是模式识别的重要方法之一。常用的有模糊C均值(fuzzy C-mean, 简称FCM)、K-means聚类、GK(Gustafson-Kessel,简称GK)聚类、谱聚类等。其中的FCM采用欧式距离计算样本之间的相似性,一般它仅适用于球形分布的数据集。GK算法引进了自适应距离范数和协方差矩阵,可以反映数据沿任意方向或子空间的分散程度,并没有改变聚类算法产生类似于球体的聚类状态[14]。GG聚类算法是FCM聚类算法和GK聚类算法被改进的结果。因其通过引入模糊最大似然估计方法来度量样本之间的距离,故可以反映不同形状和不同方向的数据类。文献[15]已将GG聚类算法成功应用于滚动轴承的故障诊断中,取得了较好的分类效果。
基于上述原因,本研究将对经验小波变换、多尺度排列熵、GG聚类算法相结合并应用于滚动轴承的故障辨识方法进行研究,欲通过实验验证所提出方法的有效性。
1 基础理论
1.1 经验小波变换EWT
EWT的核心思想是通过对信号的傅里叶频谱进行自适应分割,构建出一组适合于待处理信号的小波滤波器,以提取具有紧支撑傅里叶频谱的AM-FM成分,然后对提取的AM-FM成分进行Hilbert变换,最终得到有意义的瞬时频率和瞬时幅值,进而得到Hilbert谱。

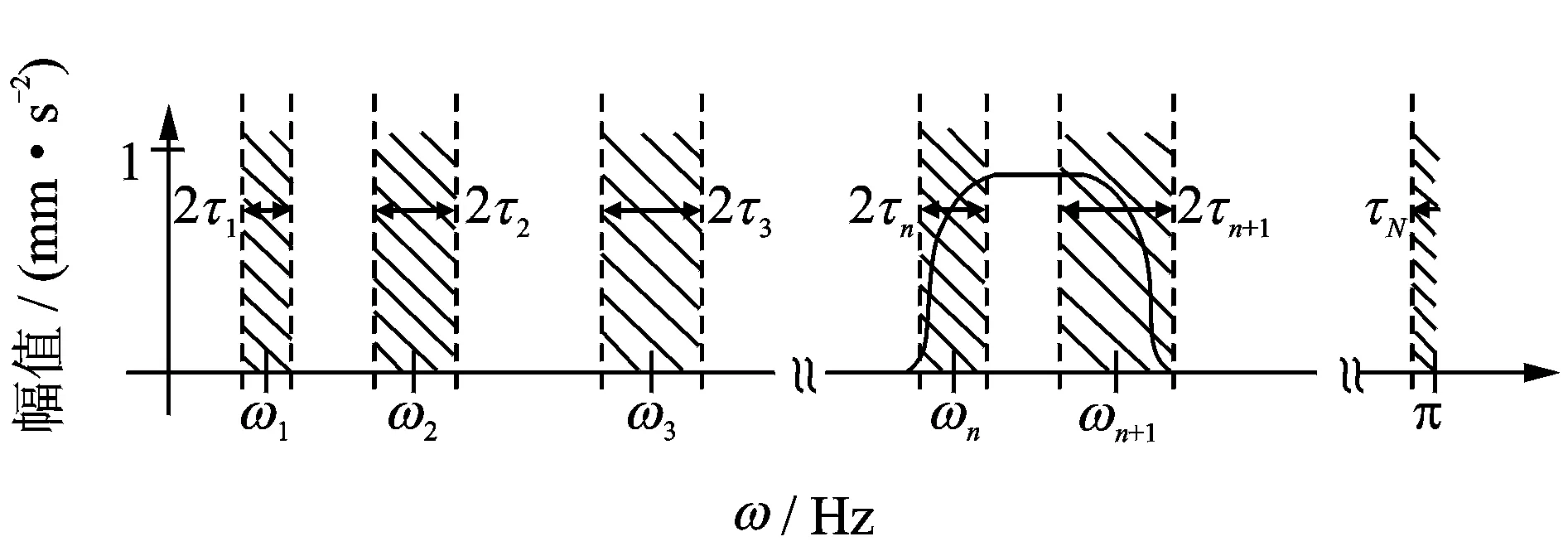
图1 傅里叶轴的分割Fig.1 Partitioning of the Fourier axis
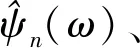
(1)
(2)
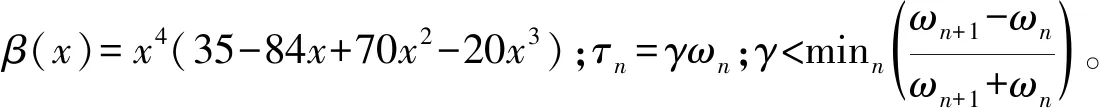
傅里叶分割的关键是确定N。除去0,π两个边界之外,文献[5]采用了易于理解的阙值法寻找其余N-1个边界。寻找的途径是通过计算频域内k个幅值极大值Mi(i=1,2,…,k),按递减排序M1≥M2≥…≥Mk并归一化它们到[0,1],规定Mk均需大于阙值Mk+α(M1-Mm),其中α为取值在[0,1]之间的相对振幅比。在α被确定之后,N为大于阙值的极大值点的个数,因此可定义大于阙值的前N个最大值所对应的ωn为N-1个边界。
重构原始信号f(t)的公式定义为
(3)
经验模态fk(t)的定义如下
f0(t) =Wf(0,t)*φ1(t)
fk(t)=Wf(k,t)*ψk(t)
经过对若干个经验模态函数进行Hilbert变换,即可得到Hilbert谱。
1.2 多尺度排列熵理论
1.2.1 排列熵算法
对于一维时间序列X={x(i)|i=1,2,…,n},设嵌入维数和延迟时间分别为m,τ,则按照Takens定理对X进行相空间重构,可得到式(4)所示的重构矩阵,即
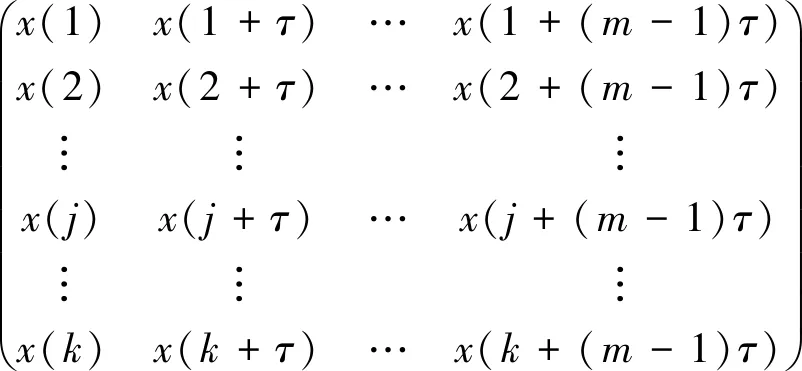
(4)
其中:j=1,2,…,K;K=n-(m-1)τ。
该矩阵共有K行,其中每一行均为一个重构分量。如果用{j1,j2,…,jm}表示重构分量中各个元素所在列的索引,则可将式(4)中的若干重构分量按升序重新排列为式(5),即
x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤
…≤x(i+(jm-1)τ)
(5)
若重构分量中有大小相等的情况,需通过比较j1和j2值进行排序;当j1 (6) 当Pj=1/m!时,Hp(m)将达到最大值ln(m!)。对Hp(m)进行归一化处理,即 Hp(m)=Hp(m)/ln(m!) (7) 显然,Hp可代表X的随机性;Hp越大,表示X的随机程度越大;反之,说明X越规则。 1.2.2 多尺度排列熵算法 该算法首先将原始时间序列进行粗粒化处理,在多个尺度上计算时间序列的排列熵,然后计算各个不同尺度下的排列熵。具体的计算步骤如下。 1) 设长度为N的原始时间序列x(i)={x(1),x(2),…,x(N)},建立的新粗粒序列为 (8) 其中:s为尺度因子。 当s=1时,粗粒化序列为原始时间序列,称为单尺度排列熵;当s=n时,原始时间序列可被分割成为N/s个每段长度为s的粗粒序列。 2) 对得到的N/s个粗粒序列,求排列熵。 文献[16]给出的GG聚类算法步骤如下。 1) 设聚类样本集合为X={x1,x2,…,xi,…,xn}。其中:元素xi具有d个特征指标。设利用隶属度划分矩阵U=(ui k)K×n作为判据,可将X聚成K类(2≤K≤n)。其中:ui k表示第k个样本隶属于第i个类别的程度。 2) 设终止容限为ε>0,随机初始化隶属矩阵为U。 3) 用式(9)计算各聚类中心,即 (9) 其中:h>1为加权指数;l为整数且l>1。 4) 计算模糊最大似然估计距离测度 (10) 其中:Ai为第i个聚类的协方差矩阵,pi为第i个聚类被选中的先验概率。 计算公式如式(11,12),即 5) 更新用于分类的隶属度矩阵 (13) 直到‖Ul-Ul-1‖<ε。 本研究提出的将EWT、多尺度排列熵、GG聚类算法相结合的新故障诊断法具备如下特点。首先,它充分利用了EWT的自适应分解和排列熵计算简单、抗噪能力强的特点。其次,利用相关系数选取EWT分解后的最优模态分量的处理方式,在减少了一定的计算量之外,将多个尺度下计算出的最优模态其排列熵作为了特征向量。针对用此方式得到的熵值特征向量存在着高维度和数据难以可视化的新问题,故随后利用主成分分析(principal component analysis, 简称PCA)进行可视化降维,最后将得到的维数低、敏感度高且分类误差率小的主要特征向量输入至GG聚类算法中去实施聚类分析。 为上述过程设计的算法步骤如下: 1) 对振动信号进行经验小波变换,得到若干个AM-FM分量; 2) 对若干AM-FM分量进行相关性分析,相关系数最大的即为最优模态分量,EMD各模态与原信号的相关性约等于各分量的自相关系数[17],因此对得到的若干固有模态分量进行相关性分析[18]并选出最优模态作为下一步故障分类和识别的样本,以达到剔除无关模态的目的; 3) 计算最优模态分量的多尺度排列熵值,经实验决定选取前9个尺度的排列熵作为特征向量; 4) 利用主成分分析对熵特征向量进行降维; 5) 将降维后的低维特征向量作为GG聚类算法的输入,并采用聚类评价指标评价聚类效果。 与上述算法对应的数据处理流程如图2所示。 图2 故障聚类方法流程Fig.2 The flow char of the fault classification method 本研究采用美国凯斯西储大学电气工程实验室的滚动轴承数据[19]对图2算法进行验证。轴承型号为SKF公司6205-2RS深沟球轴承。电机功率约1 494 W,转速1 730 r/min,采用电火花加工技术在轴承上布置单点故障,凹坑的直径×深度=0.177 8 mm×0.297 4 mm。设置的采样频率为12 kHz,采集{滚动体故障(rolling element fault, 简称REF),内圈故障(inner race fault, 简称IRF),外圈故障(outer race fault, 简称ORF),正常(NORM)}={REF, IRF, ORF, NORM}这4种状态下的振动信号各50组,每个信号长度为2 048。 随机选取滚动体故障信号进行分析。图3是经过EWT自适应分解后得到的10个AM-FM分量情况,表1是相关系数的计算结果。可以看出,C7与原始振动信号的相关系数最大为0.856 6,因此选择C7为最优AM-FM分量进行下一步的故障分类和识别。 图3 滚动体故障EWT处理结果Fig.3 Rolling element failure EWT processing results Tab.1 AM-FM component and correlation coefficient of the original signal 分量序号相关系数分量序号相关系数C10.121 5C60.462 5C20.153 2C70.856 6C30.135 2C80.064 8C40.120 3C90.037 3C50.068 5C100.029 2 在计算多尺度排列熵时,需设定的参数有:时间序列长度N、嵌入维数m、时延τ和尺度因子s。其中,推荐的m=3~7[13]。m过大,将增大计算时间且无法反映序列的细微变化;m过小,重构序列中可能包含的状态会太少,则难以检测出时间序列的动态突变;经过权衡,本研究中选取m=4。图4为不同τ时的排列熵变化情况。可看出,τ对信号熵值的影响较小,故选取τ=1。取s=12,计算12个粗粒向量的排列熵,得到的4种状态结果见图4。 图4 滚动轴承信号在不同时延下的排列熵Fig.4 Arrangement entropy of rolling bearing signals at different times 图5是4种故障随尺度因子s增大时最优模态的多尺度排列熵变化情况。显然,当s=1、即单一尺度排列熵时,虽然正常状态与故障状态的熵值区别明显,但是3种故障状态的熵值很接近,此时很难区分3种故障状态,因而需要对最优模态分量进行多尺度分析。由于前几个熵值表征了EWT最优模态的主要信息,通过实验决定采用前9个尺度的排列熵值作为特征向量。 图5 EWT最优模态的多尺度排列熵Fig.5 The optimal modal of multi-scale EWT permutation entropy 对滚动轴承的4种状态分别进行EWT分解并通过相关性分析选取最优模态分量,在9个尺度下计算最优模态分量对应的排列熵作为特征向量,可得到4组50×9的排列熵。采用极大似然估计法,用PCA算法将特征向量从9维降至3维。因为有4种状态,故聚类中心个数初步设定为4个,设加权指数h=2、迭代终止容差ε=0.000 1。将经PCA降维后的特征向量输入GG聚类算法,得到的结果如图6所示。 图6 EWT多尺度排列熵的GG聚类等高线图Fig.6 The GG clustering contour for EWT multi-scale dimension permutation entropy 图6中,V1~V4分别是{REF, IRF, ORF, NORM}4种状态的聚类中心,它们的聚类中心坐标值见表2。从图6可看出,滚动轴承的4种不同状态不仅被明显地分开、而且各类别均聚集在聚类中心附近,即聚集紧密、没有出现不同类别相互混叠的现象,类间距较大。各组样本集合的隶属度平均值见表3。从表3可看出,第1组样本对于V3的隶属度远大于其他3组,说明第1组样本隶属于V3类,辨识效果良好。同理,第2~4组样本分别可归属于V1,V4和V2类。 表2 4种不同类型信号的聚类中心 Tab.2 The clustering centers of the four different typessignals 样本组号聚类中心xy内圈故障V10.103 90.473 2外圈故障V20.667 50.648 1滚动体故障V30.961 80.540 0正常状态V40.754 30.177 3 表3 4种不同类型信号的隶属度 为进一步验证节2所提方法的有效性,本研究还采用直接对原始振动信号进行多尺度排列熵计算和EWT分解后提取单一尺度排列熵作对比试验,并把结果分别输入FCM,GK,GG聚类算法,得到的聚类结果如图7所示。通过对比分析得到的结论如下。 1) 将图7(a)、图7(b)与图7(g)、图7(h)进行对比可以得出,直接对原始信号进行多尺度排列熵提取得到的特征向量经FCM,GK聚类算法处理的聚类效果不理想,而经EWT多尺度排列熵提取的特征向量聚类效果较好。显然,这应该是原始信号经EWT消噪、保留了更多故障信息的结果,故聚类效果较好。 图7 不同模式组合下的2维聚类效果图Fig.7 Different mode combination 2 dimension clustering results 2) 图7(d)与图7(e)聚类效果不佳。这是因为单一尺度排列熵并不能很好地表征故障状态,而且经过EWT后并没有筛选出最优模态分量,没有去除冗余信息,这对聚类效果造成了一定的不利影响。 3) EWT多尺度排列熵组合较其他组合模型,其聚类结果的类内紧致性最好。图6、图7(g)和图7(h)的聚类中心基本吻合,图7(a)、图7(d)的聚类中心不一样,说明聚类方法对聚类中心的影响较小,而聚类中心与输入的特征向量有关。 总体而言,如果从聚类等高线的角度去评价,则FCM聚类的等高线接近于圆球形;GK聚类的等高线类似于椭圆;而GG聚类的等高线,应该说具有等高线形状不确定的特点。 使用分类系数(ppartition coefficient, 简称PC)和划分熵(classification entropy, 简称CE)这两个测度评价[16],对图6、图7不同聚类模型的聚类效果评价结果见表4。 表4 不同模型FCM,GK,GG的聚类指标 根据表4可得到如下推论:a.相对于FCM和GK聚类,GG聚类具有明显的优势,这是由于FCM聚类的圆球形,它仅反映超球形数据结构的标准距离规范;b.GK聚类的椭球形仍近似于球形;c.GG聚类因为聚类形状是任意形状的,故聚类效果可以反映出数据集的分散程度;d.EWT多尺度排列熵组合在GG聚类中,PC值最大达到了1,CE值最小为NAN。由此看出,EWT多尺度排列熵组合较其他模式组合而言具有一定优势,因此本研究提出的方法具有良好的滚动轴承故障分类与辨识性能。 经验小波变换是近几年来兴起的一种新自适应信号处理方法。它具有计算简单、计算速度快、理论基础完备的特点。在此基础上,提出了一种经验小波变换、多尺度排列熵、GG聚类算法相结合的故障诊断方法,并把它应用到滚动轴承的故障诊断中。该方法首先采用EWT对原始信号进行分解、得到若干个固有模态分量,通过计算各个分量与原始信号的相关系数,选取最优模态分量以剔除冗余信息,对最优模态分量进行多尺度的排列熵计算,由于得到的熵值特征向量具有高维度和数据无法可视化问题,故采用PCA进行降维之后再输入到GG聚类算法中。实验证明,本研究提出的故障诊断方法能够较好地区分滚动轴承的不同状态,故障类间无重叠,是一种有效的自适应故障特征提取和故障数据聚类与分类方法。1.3 GG聚类算法
2 设计的故障辨识方法
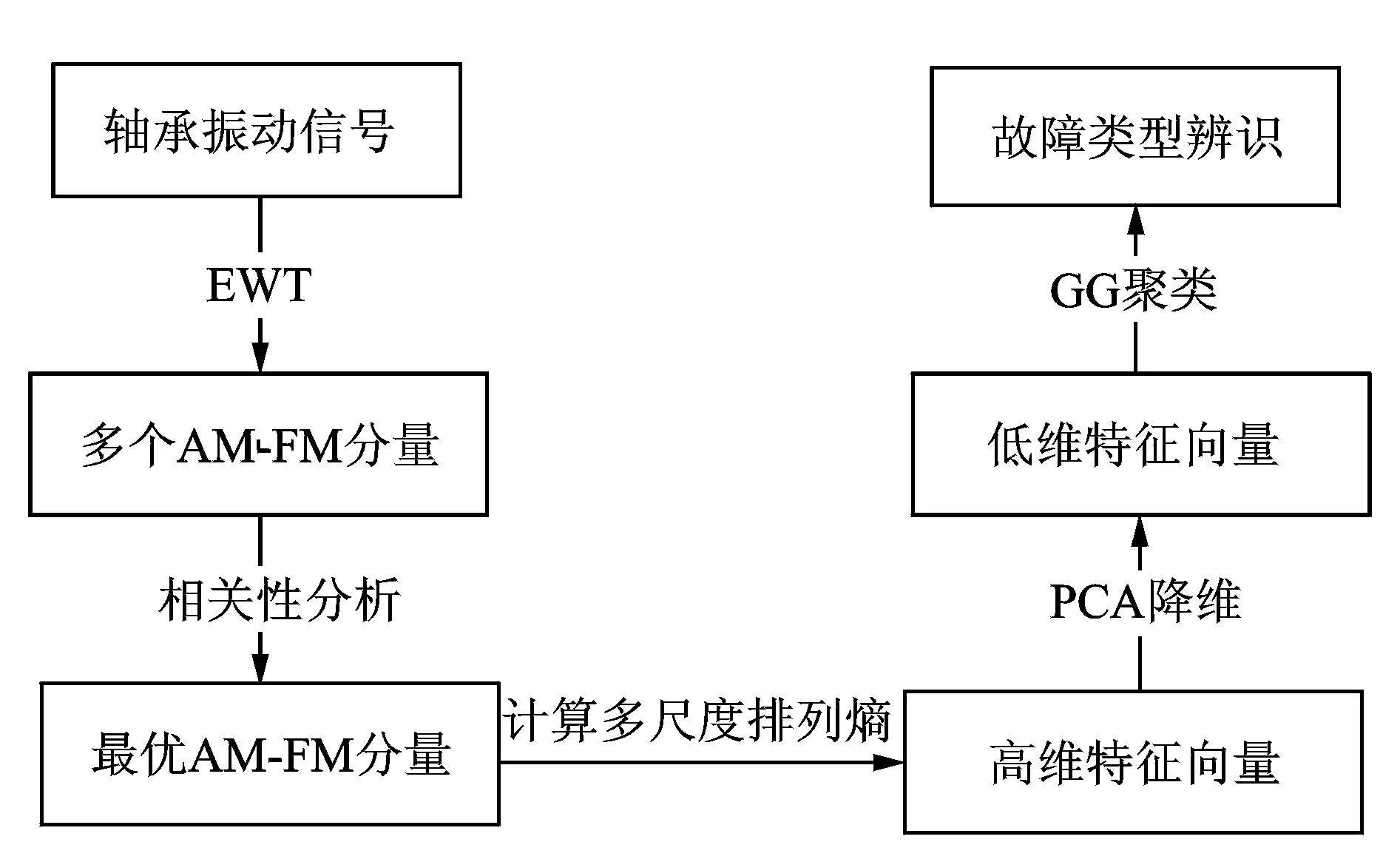
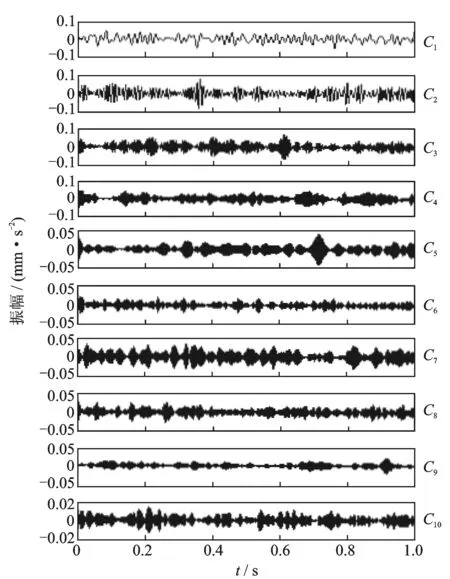
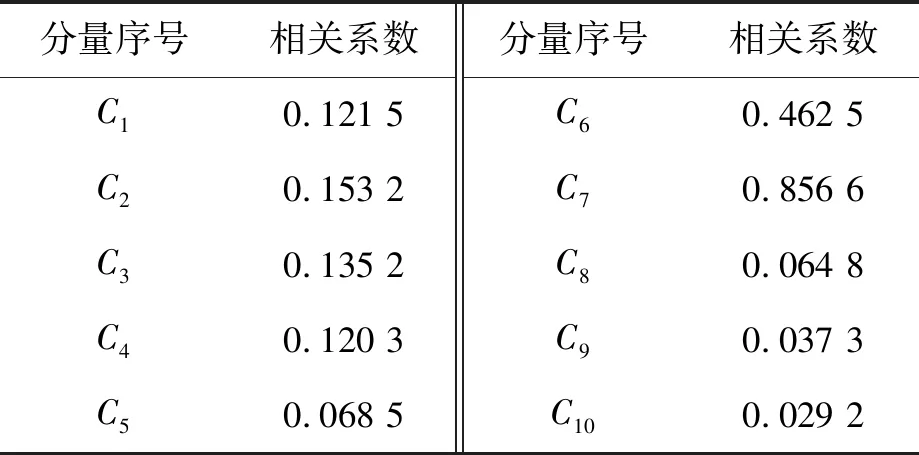
3 实例分析

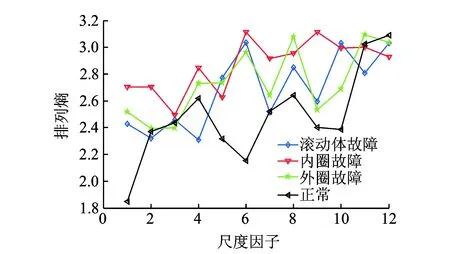
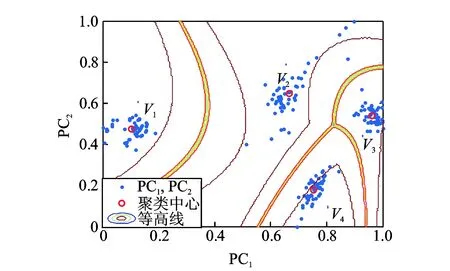
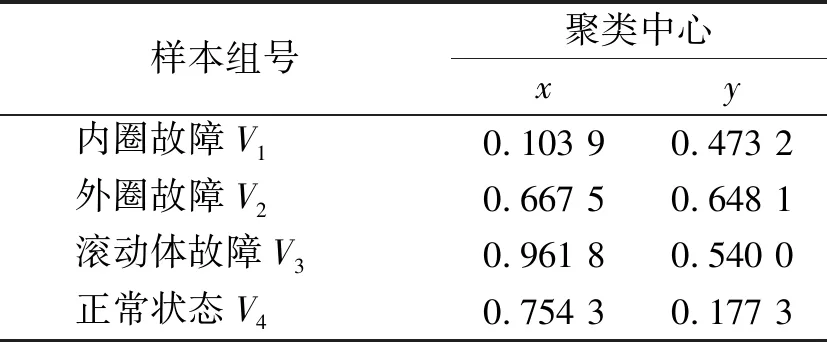

4 结束语
