磁悬浮压缩机顶隙调压模型与实验*

韩邦成， 崔炳伟， 郑世强， 张 寅, 宋欣达

(1.北京航空航天大学惯性技术重点实验室 北京，100191) (2.北京市高速磁悬浮电机技术及应用工程技术研究中心 北京，100191)

引 言

磁悬浮离心压缩机是采用磁悬浮透平技术的压缩机设备，将压缩机增压部分安装在电机的延伸端上，实现了高速电机直接驱动，能够同时满足大容量和大压力的要求。但是，与传统压缩机相似，风压紊乱带来的故障也会对磁悬浮压缩机产生严重的损害：a.故障往往具有迟滞现象，使得立即解除这些不稳定状态较为困难，造成恶性循环；b.磁轴承轴向受力不均匀，导致轴向磁轴承振动甚至失稳，对磁悬浮压缩机造成严重磨损；c.风压紊乱还会造成磁悬浮压缩机性能严重恶化，轻则引起震动噪声，重则导致机组瘫痪[1]。喘振是最常见的一种压缩机风压紊乱造成的故障，当喘振发生时，压缩机出口的压力由于流量的损失而降低，而管网内的压力由于迟滞并不能及时下降，造成管网压力大于压缩机出口压力，引起流量的回流，回流的气体会对压缩机的叶片等部位施加力的作用，影响压缩机正常工作，对压缩机产生严重损害。旋转失速是气流冲角达到临界值附近时，气流离开叶轮而造成风机风压降低的现象，旋转失速在严重时也会造成喘振的危害。可见多数风压紊乱造成的故障与压缩机蜗壳出口压力的改变有着直接的关系。

学者们针对风压紊乱引起的喘振等故障的发生机理及防治进行了一系列的研究[1-4]。传统压缩机一般通过转速调节[5]、进出口节流调节[6]、叶轮结构、扩压器结构变化等方式调节压缩机的压力。文献[7]在传统压缩机上进行了针对压缩机顶隙与压缩机出口压力关系的数学模型建立及相关实验，证明了顶隙对压缩机出口压力有影响。在磁悬浮压缩机的风压调节方面，文献[8]提出磁悬浮压缩机可以通过调节叶轮顶端与蜗壳之间的间隙对压缩机出口风压进行调节，为本研究的开展指明了方向。文献[9]通过磁悬浮压缩机位置传感器采集的位移信号对于喘振的产生进行了有效检测，为磁悬浮压缩机风压调节研究的开展奠定了基础。文献[10]使用一种基于H∞算法的主动磁轴承控制算法并对压缩机调压模型进行了分析，但研究局限在喘振的仿真，缺少应用于压缩机的研究及试验。通过上面的分析可以看出，传统压缩机结构固定，对于通过叶轮顶隙抑制风压紊乱的研究极少，而通过磁悬浮压缩机轴向主动磁轴承实现风压调控的研究还停留在理论阶段，缺少相应的实验研究。

为解决磁悬浮高速离心式压缩机系统的风压调节问题，笔者进行了相关的理论研究及实验分析。从轴向主动磁轴承调节磁悬浮转子位置的工作原理角度分析风压调节的可行性，从流体能量方程出发建立叶轮顶隙与出口风压之间的数学模型，通过“间隙改变对压缩机蜗壳出口风压影响”实验对顶隙改变调节风压的特点进行分析并对所建立的模型进行验证。

1 轴向磁轴承工作原理及控制分析

图1为磁轴承磁路模型图，缠绕在极靴上的线圈通入电流后，根据电磁感应定律，模型中的悬浮体将受到磁力的作用。根据虚位移定理、麦克斯韦方程可推导得到磁悬浮转子所受力的数学模型

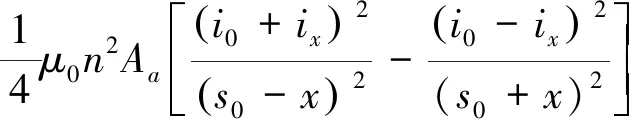
(1)

其中：n为线圈匝数；s为磁间隙；lf e为导磁体回路长度；Aa为气隙截面积；Af e为线圈截面积；μ0为真空磁导率；i为总输入电流；i0为偏置电流；ix为控制电流；s0为转子在平衡位置时的位移；x为转子偏离平衡位置处的值。

图1 磁轴承磁路模型Fig.1 Magnetic path model of magnetic bearing

在具体设计时，主动磁轴承采用二对极设计，各通道采用偏置差分结构，如图2所示。当磁悬浮转子在平衡位置作小位移运动时，将电磁力在平衡位置处Taylor展开，忽略高次项后，可对数学模型线性化为

Fm=khx+kiix

(2)

图2 轴向磁轴承结构模型Fig.2 Structural model of axial magnetic bearing

其中：kh，ki分别为位移刚度及电流刚度。

(3)

通过模型可以看出，磁悬浮轴承对转子的作用力同时受到偏置电流及转子位置的影响。磁悬浮轴承系统对转子进行控制的模型如图3所示。其中：fi为数学模型中电流项产生的力；fh为模型中位移项产生的力；fd为干扰力；xh为位置信息；uc为控制信号。

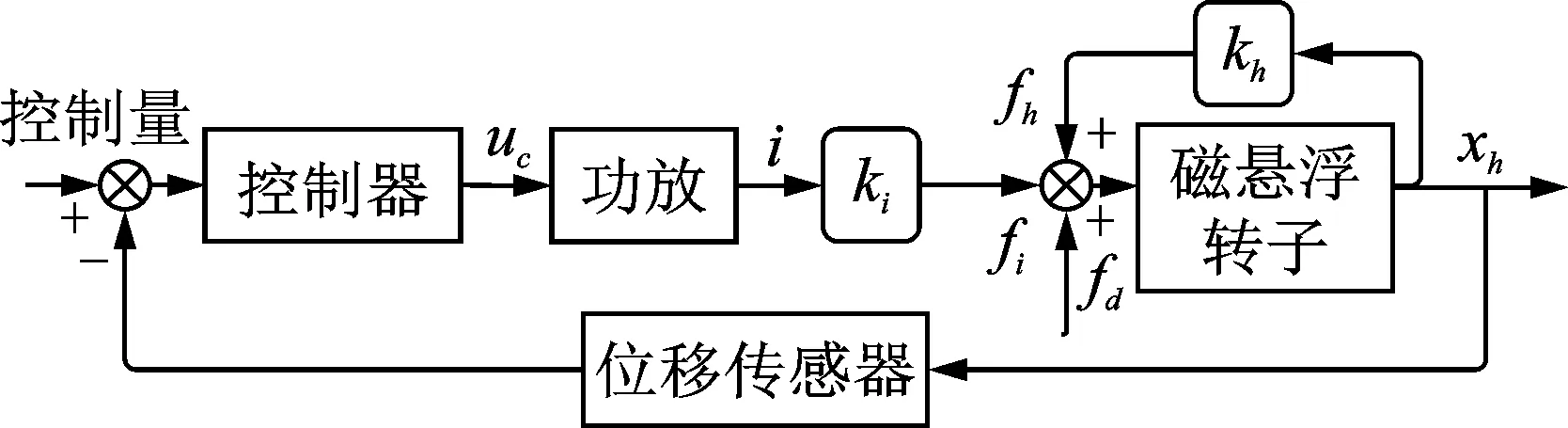
图3 磁悬浮转子控制模型Fig.3 Control model of magnetic levitation rotor

由于磁轴承控制过程的开环不稳定性及转子运行过程中干扰力fd的影响，磁悬浮轴承系统位置传感器需要实时的将转子位置信息xh输送回控制器并与输入的控制量比较，控制器将差值解算并产生对功放环节控制的控制信号uc，功放环节在控制信号的指挥下，通过外部电源产生作用于磁悬浮轴承线圈的电流i，在线圈产生的电磁力作用下，实现磁悬浮转子的悬浮或位置调整。当前，对于磁悬浮轴承控制系统的研究已经比较全面，既有PID控制[10]等常规控制方法，也有H∞控制[11]、基于趋近律的滑模控制[12]等鲁棒控制方法。因此，在磁悬浮压缩机中通过轴向主动磁轴承对转子位置进行调整，从而实现压缩机蜗壳出口风压的调节是完全可行的。

2 叶轮顶隙调模型

磁悬浮压缩机系统可以通过位移传感器对风压状况进行早期监控。同时，还能通过改变转子轴向位置对叶轮与压缩机蜗壳之间间隙进行调整，有效调节压缩机出口风压，实现对故障的早期预防。笔者对其原理分析如下: 压缩机工作时其气体为Ma<0.3的低速流动，气体的密度变化有限。如图4假设进入压缩机的气体压强为P1、气体的流动速度为v1，流出压缩机的气体压强为P2、气体流动速度为v2，气体叶轮上进行离心运动时获得的能量为W1，各种损耗的能量和为W2，通过气体压缩机获得的净能量为ΔW，气体的流量为qv。

图4 磁悬浮压缩机蜗壳模型Fig.4 Volute model of magnetic levitation compressor

那么依据气体的伯努利方程及能量守恒原理并忽略气体的势能变化之后，可以得到

(4)

(5)

(6)

气体压缩过程中的功主要用于提高压力及流体流速，压力的提升称为静压升高，流体速度的提升称为动压升高。依据压缩机的原理及伯努利方程可知,压缩后气体无论动压升高还是静压升高均来源于流体流经叶轮时的流速的升高。基于该原理，笔者提出使用无量纲压升系数Ψ，建立压缩后气体风压与流入压缩机蜗壳风压的关系式，并假设最主要的影响因素为压缩机叶轮的转速，基于该假设笔者建立压缩后气体压力与压缩机转速的数学模型如下

(7)

其中：P2为增压后的压力；P1为入口的压力；ρ为气体的密度；U为磁悬浮压缩机叶轮的转速。

静压与动压之和称为全压，全压能的提高与气体在压缩机中的压缩过程有关。实际的压缩过程为有损失并且与外界有热交换的多变过程，气体按多变压缩过程压缩时多变指数是变化的，用平均的多变指数m来代替变化的多变指数，称压缩过程中所需要的功为压缩功，则多变过程的压缩功模型为

(8)

其中：m为平均多变指数(一般取1.4)；R为气体的普适恒量；T为气体的华氏温度。

Senoo等[13]研究了单级离心压缩机中不同顶隙的对压缩功的影响，并提出了一个简单的数学模型描述了叶轮和蜗壳之间间隙与压缩功的关系，其模型如下。

(9)

其中：W0为顶隙c=0时的理论压缩功；W1为顶隙增加到c1之后的理论压缩功；h0为压缩机叶轮叶片高度。

设间隙增加δc变为c2，此时理论压缩功为W2，并加入实验获得的阀门修正系数v后，由式(9)推导可以得到

(10)

设顶隙变化前通过离心压缩机增压后的静压为Pc1，无量纲压升系数ψ1，那么式(7)变为

(11)

将其带入压缩功表达式得到

(12)

同理，设顶隙变化后通过离心压缩机增加的静压为Pc2，无量纲压升系数为ψ2，可以得到

(13)

将式(12,13)带入式(10)可以得到

(14)

间隙改变过程中时间较短，改变前与改变后温度变化不大，即T1=T2，因此数学模型变为

(15)

由式(15)便可以得到顶隙c变化后压升系数ψ的变化，进而可以得到顶隙变化后的静压升高，δc的取值也为风压的调控提供了参考。

3 实验平台及主要参数

文中以功率为30 kW的压缩机为实验对象，进行了“间隙改变对压缩机蜗壳出口风压影响”的实验。实验平台如图5所示，其主要参数见表1。

图5 30 kW磁悬浮压缩机实验平台Fig.5 30 kW compressor experimental platform

参 数值压缩机额定转速/(r·min-1)48 000压缩机设计极限流量/(m3·h-1)3 500压缩机设计增压比1.68叶轮高度/mm148磁轴承设计间隙变化范围/mm0.2叶轮与蜗壳之间间隙/mm15

磁悬浮压缩机运行过程中，径向磁轴承及位于下端的轴向磁轴承对悬浮的转子起支撑作用，转子轴直接与叶轮相连接。当电机带动叶轮旋转时，进入压缩机本体的气体经叶轮带动而增速，增速后的气体在蜗壳内实现增压并将增压后的气体输送到出气口，完成压缩过程。实验平台中，电机控制器用于控制转子升速并使其稳定在需求转速；磁轴承控制器用于将转子稳定悬浮并改变转子位置，通过上位机可以对转子位置实时控制实现叶轮与蜗壳之间间隙的改变；阀门用于模拟压缩机的工作状态，不同的阀门开度代表压缩机工作于不同的流量状态；流量计用于采集进入压缩机的气体流量，压力计用于采集压缩机气体的出口压力，温度计用于采集压缩机进出口的温度；流量计、压力计、温度计连接到S7-200PLC用于采集流量、出口压力及进出口温度数据。

4 实验过程及数据分析

磁悬浮转子悬浮于指定位置作为间隙调节的初始位置进行压缩机的升速实验，在管道出口阀门分别关紧20%，50%，80%情况下，将压缩机转速稳定在6 000, 8 000, 10 000, 12 000, 14 000， 16 000， 18 000， 20 000, 22 000, 24 000及26 000 r/min左右时进行压缩机出口压力、流量、进出口温度的采集。阀门开度50 %情况下，将压缩机转速稳定在5 000, 10 000, 15 000, 20 000及25 000 r/min左右时，通过改变转子轴向位置调节叶轮与蜗壳之间间隙，考虑到磁轴承的保护间隙只有0.2 mm，分别对初始位置、间隙减少0.1， 0.2 mm时压缩机蜗壳出口压力、流量及进出口温度进行采集。

图6展示了阀门关紧不同程度时转速升高对出口风压及流量的影响。从图6可以看出，当转速改变时，磁悬浮压缩机的出口增压压力会发生明显的改变，同时转速对增压影响的曲线与二次函数曲线相似度较高。因此提出数学模型时，假设压缩机的出口增压主要受到压缩机转速的影响是合理的。

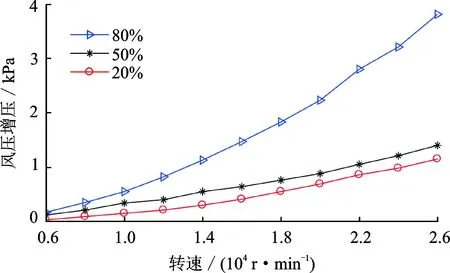
图6 阀门关紧20%，50%，80%时风压增压随转速变化图Fig.6 Variation of pressure boost with speed when the valve is closed 20%, 50%, 80%

结合统计学中单因素试验方差分析的原理对实验数据进行定性分析如下：间隙改变作为唯一的实验变量，将相同转速下间隙不变、间隙改变0.1及0.2 mm时风压增压数据分为3组，表2是对不同转速下增压数值的组内平方和与组间平方和的比较。

从多组数据处理的结果可以看出，“组间差值平方和”远大于“组内误差平方和”，因此可以断定因素“叶轮与蜗壳之间间隙改变”对“磁悬浮压缩机蜗壳出口压力”有显著的影响。间隙减小时风压增加，间隙增大时风压减小，因此通过调节叶轮顶端与蜗壳之间间隙对风压进行调控具有可行性。

表2 组内误差平方和与组间差值平方和比较

Tab.2 Sum of squared error and sum of squares between groups

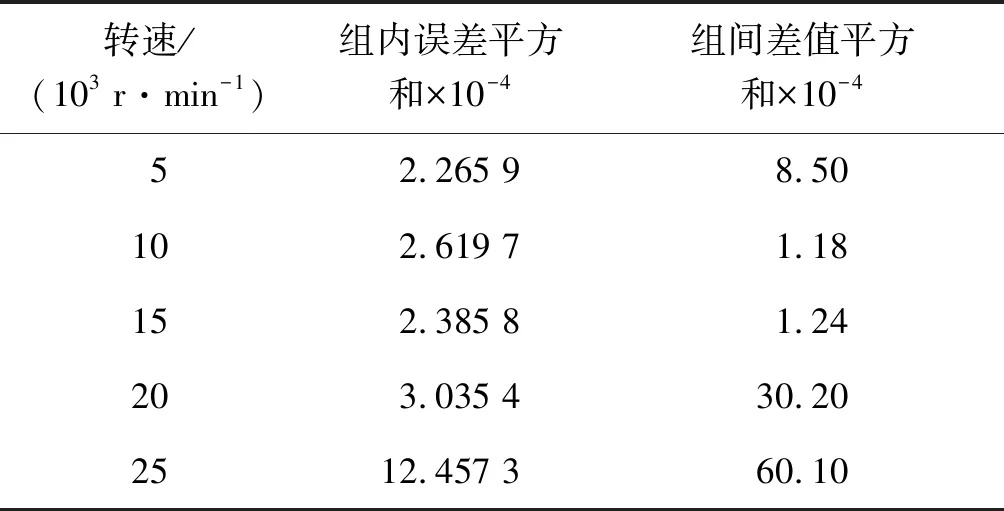
转速/(103 r·min-1)组内误差平方和×10-4组间差值平方和×10-452.265 98.50102.619 71.18152.385 81.24203.035 430.202512.457 360.10

图7为阀门50 %开度时蜗壳出口增压实验值与模型计算值的比较。从图7可以看出，当间隙改变前出口风压值相同时，间隙改变(0.1， 0.2 mm)后模型计算与实验得到的出口风压值相差较小，在阀门修正系数合理地情况下，误差能控制到9.5 %以内。因此，通过模型得到的风压变化值可以作为风压调控的依据。

图7 模型计算压力与实验数值比较Fig.7 Compare the calculated and experimental values of the pressure

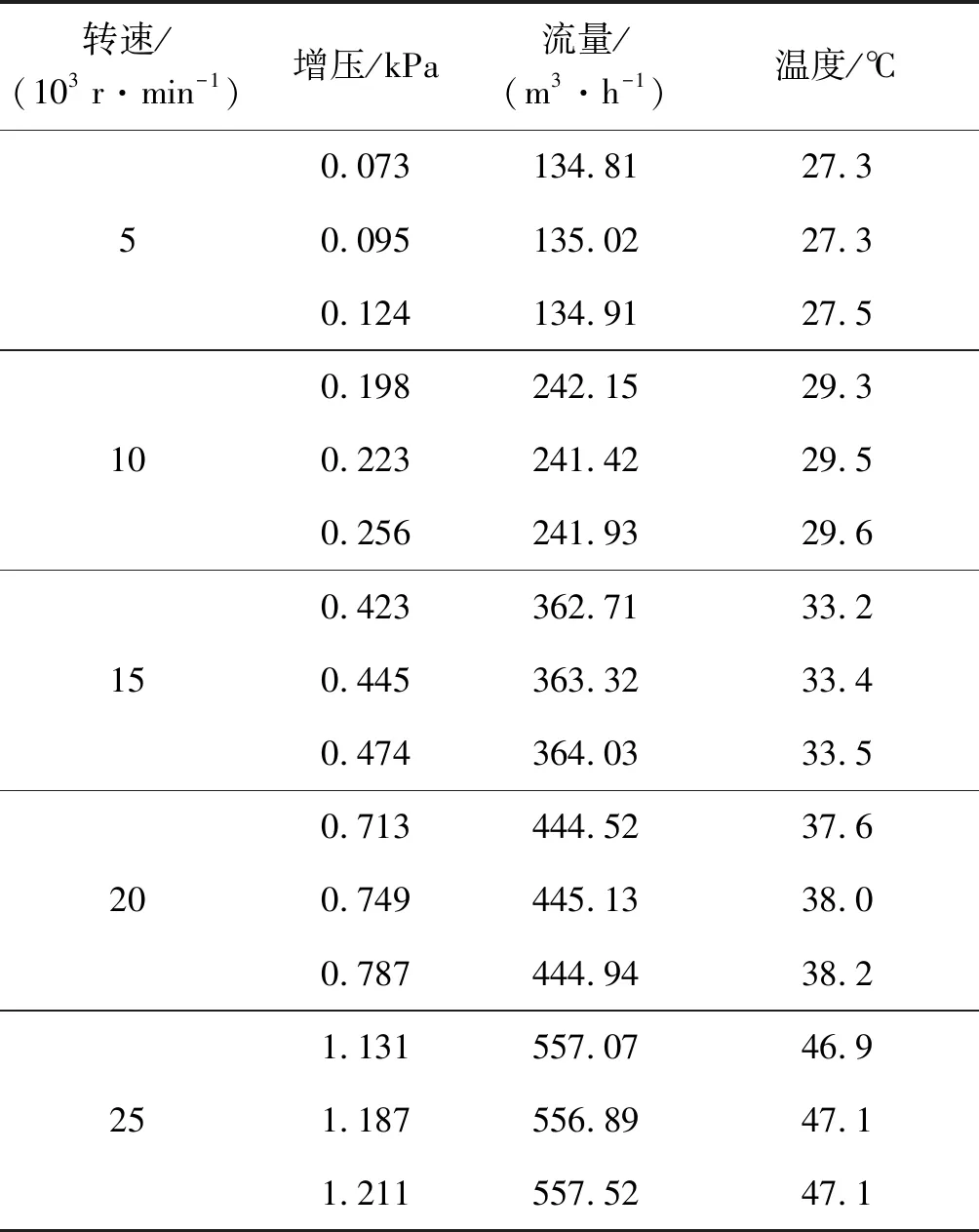
表3是间隙改变后出口增压、流量及出口温度的变化值，相同转速下依次为间隙不变、间隙减小0.1 mm及间隙减小0.2 mm时得到3组数据。从表中可以看出，随着出口风压的增加，间隙对风压的影响更加明显，而对压缩机的流量影响较小。单独的升速实验表明，出口气体温度的升高主要与工作时间有关，间隙改变几乎对其无影响。因此通过改变间隙对风压进行调控可以实现对风压的单独调节，而不会引起流量及出口温度的明显改变，在工程中更加实用。

5 结束语

以磁悬浮压缩机为主要的研究对象，建立了叶轮顶隙变化与蜗壳出口风压之间关系的数学模型，并通过实验证明了模型的准确性。实验证明，风压调节过程对流量、温度等参数产生的影响较小，实现了对风压的有效调节。运用笔者的研究成果并结合磁悬浮压缩机在工况检测方面的优势，可以在故障发生的早期对喘振等恶劣工况进行有效的控制，具有很高的工程价值。

表3 间隙改变后出口增压、流量及出口温度的变化值

Tab.3 The change of outlet pressure, flow rate and outlet temperature after clearance change

转速/(103 r·min-1)增压/kPa流量/(m3·h-1)温度/℃50.073134.8127.30.095135.0227.30.124134.9127.5100.198242.1529.30.223241.4229.50.256241.9329.6150.423362.7133.20.445363.3233.40.474364.0333.5200.713444.5237.60.749445.1338.00.787444.9438.2251.131557.0746.91.187556.8947.11.211557.5247.1