基于PZT结Lamb波方向算法的损伤定位方法*

赵竹君, 李 成, 侯玉亮, 铁 瑛, 宋成杰

(郑州大学机械工程学院 郑州,450001)

引 言

Lamb波是在具有自由边界的固体板或层状结构中传输的一种弹性导波，由于其本身的传播特性，如沿传播路径衰减小，能量损失小，传输距离远等，成为现行无损检测领域研究的重要手段。对于由碳纤维增强树脂基复合材料制造的航空航天结构，Lamb波的应用则更为普遍。在对其进行无损检测时，采用何种损伤检测工具及方法非常重要。

在损伤检测过程中，检测工具通常采用压电换能器(piezoelectric transducers，简称PZT)，PZT的轻薄特性使之在超声无损检测中得到广泛的应用。Matt等[1]证明当PZT直径与Lamb波波长之比足够小时，其可被视为完美的检测工具。蔡建等[2]通过双面激励法，即在板的上下表面分别布置PZT，有效抑制了Lamb波的多模式特性。Wandowski等[3]研究了PZT的不同布置方式对损伤定位结果的影响，并证明了PZT在损伤检测中比激光测震计具有更高的敏感性。近些年，Lamb波损伤检测的方法有了很大的发展。Hay等[4]提出概率成像方法对损伤进行成像定位。孙亚杰等[5]利用超声相控阵技术对复合材料结构进行损伤识别。冯勇明等[6]利用时间反转方法对复合材料结构进行损伤检测，并用改进的RAPID算法进行损伤成像。

笔者以复合材料板的损伤定位为研究对象，在板上布置PZT 结对结构损伤进行定位检测，通过选择PZT结的布置位置以及PZT结的数量，运用互相关算法提取出损伤散射信号并用PZT结中各PZT接收损伤散射信号的位移差，找到遇损伤发生散射的Lamb波方向，多个PZT结即可确定多个方向，根据找到的损伤方向得到损伤位置。

1 PZT结损伤判定原理

1.1 损伤方向算法

由于Lamb波在板中传播时遇到损伤会产生散射，因此可以在散射方向的合适位置布置相应的PZT结，以得到板中经由损伤位置散射过来的Lamb波信号。为确定损伤的准确位置，至少需要两束由损伤位置散射而来的lamb波响应信号，如图1所示。如果可以得到两个损伤散射方向，则其方向交点即为损伤位置。通过运用由3个PZT组成的PZT结，图1中P1,P2,P3组成PZT结1；P4,P5,P6组成PZT结2。运用损伤方向算法，可以求出图中θ1,θ2的角度，从而确定损伤散射的其中两个方向。同理，如果有3个及以上多个PZT结，将得到多个损伤方向，任意两个损伤方向的交点都为损伤位置中心。在对损伤方向进行求解时，各PZT应呈三角形布置，且PZT之间间距不宜过大，最小为两PZT半径之和。

由于复合材料薄板尺寸为l×w，以板的中心为原点，长边为x轴，短边为y轴，建立坐标系，PZT结的各PZT中心坐标为(xi,yi)(i=1,2,…,6)。选取各PZT结中最先接收到损伤信号的PZT为基准，其坐标为(xb,yb)。损伤信号到达各PZT的时间为ti，到达基准PZT的时间为tb。以一个PZT结为例，则有Δti=ti-tb，由Lamb波在板中传播的速度v可得Δli=Δti·v，以基准PZT的中心为圆心，Δli为半径画圆，如图2所示，分别过PZT结中另外两个PZT的中心做圆1，2的切线m1，m2，其斜率分别为k1，k2。理想状态下m1∥m2,结合波的传播理论，则损伤信号的方向为与m1，m2垂直的方向。

现依据各点在坐标系中位置可推导出损伤方向的计算表达式。由分析可得，以基准PZT的中心为圆心的圆方程为

(1)

过第i个PZT中心做圆切线方程为

ki-y-kixi+yi=0

(2)

点到直线的距离公式为

(3)

基准PZT中心到过点1的圆切线距离为Δli，得

(4)

(5)

设损伤方向为kd，则有kdki=-1。

1.2 损伤信号的提取

在Lamb波无损检测过程中，PZT分别采集损伤前后两种响应信号，损伤前信号为结构健康响应信号，损伤后信号为结构损伤信号。Lamb波在板中传播过程中发生边界反射，因此损伤后的响应信号中不仅包括Lamb波遇损伤散射的损伤散射信号，还有Lamb波遇边界反射的信号。通常损伤散射信号的提取是根据健康响应信号和结构损伤信号之间的差异，由于Lamb波在传播时其散射信号会出现衰减，且会出现多模式混叠现象，单纯的以有损信号与无损信号相减无法得到实际的损伤散射信号。结构健康信号与结构损伤信号在同频条件下，时域上具有不同特征，存在不相关性，但二者皆由同一窄带激励信号激励，因此，激励信号作为损伤前后响应信号的基本单元与响应信号在时域上具有相同特征，通过相关性的计算分别提取出损伤前后响应信号与激励信号之间的差异，其二者的差值即为损伤散射信号。设两列信号为α(t),β(t)，则两列信号的互相关函数定义式为

(6)

它表征了对各态历经随机过程中，信号β(t)对信号α(t)的依赖程度。在τ=τ0时，R(τ)达到最大值，此时两信号之间的时间间隔为τ0，即两列信号的时间延迟为τ0，此时信号β(t)对信号α(t)的依赖程度最大，即两列信号相关性最强。设激励信号为fb(t)，压电片接收到的响应信号为f(t)，以激励信号为基准，将响应信号与基准信号做互相关运算，互相关函数达到最大值时，对应的时刻为τ0，此时响应信号与基准信号相关性最强。同时，求出基准信号的自相关函数，互相关函数与自相关函数二者最大值的比值为响应信号中基准信号幅值ab。τ0与ab可表达为

(7)

其中：〈,〉表示相关运算。

(8)

设结构健康响应信号为fh(t)，结构损伤信号为fd(t)，与激励信号分别作互相关运算，设τ1，τ2为fh(t)，fd(t)中激励信号fb(t)的出现时刻,abh为fh(t)中激励信号fb(t)的幅值，abd为fd(t)信号中激励信号fb(t)的幅值。根据式(7)可得

(9)

(10)

2 实 验

2.1 实验系统的搭建

本实验系统采用传统的Lamb波激励和接收装置，系统装置如图3所示。该系统包括NI PXI5421 任意波发生器、HA-205 电压放大器以及 PIC 255型PZT换能器，接收仪器包括 PZT 传感器、PXIe5122 数字化仪，任意波发生器和数字化仪均是由 PXIe8840 控制器控制，波形发生器和数字化仪与 PZT的连接均是通过GTP-150A-2探棒。系统通过任意波发生器产生的输入信号再经电压放大器放大后进入 PZT 激励器，PZT 激发的Lamb波信号在复合材料板中传播一段距离后由 PZT 接收器接收，并由数字化仪对数据进行采集保存到计算机中。实验中波形发生器产生的激励波形为加汉宁窗调制的5周期正弦波，频率为f0(300 kHz)。

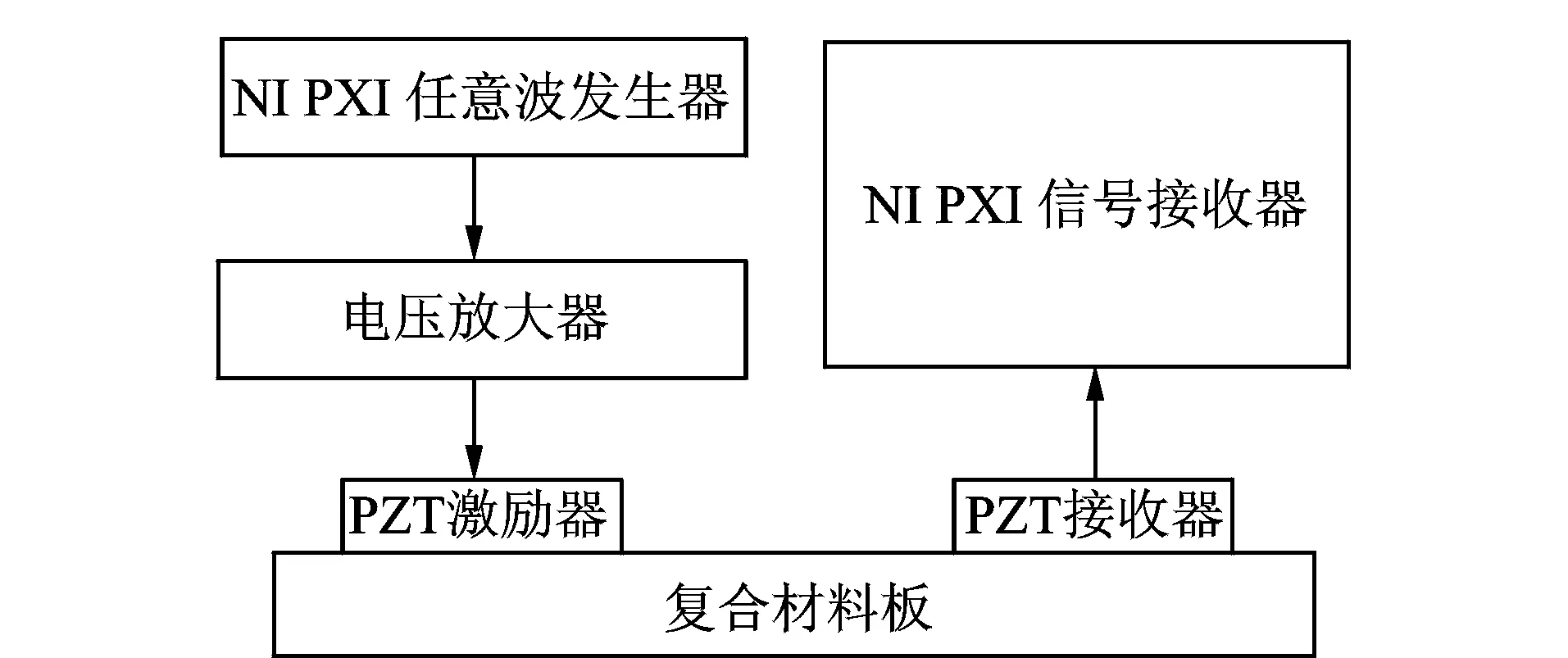
图3 实验系统装置Fig.3 Experimental system devices

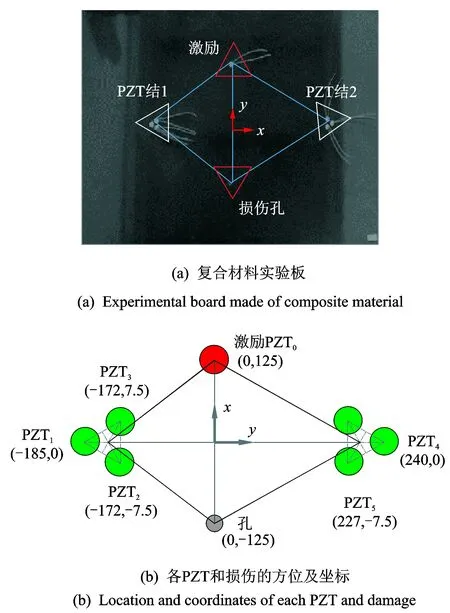
图4 实验试件及各PZT和孔位置Fig.4 Test specimen and location of PZT and damage

实验所用的试件，如图4(a)所示：24 层的碳纤维增强树脂复合材料矩形板长为 720 mm，宽为 500 mm，在其上粘贴有2组PZT结与1个激励PZT，实验中的损伤设置为典型的通孔损伤，采用电钻钻出直径为6 mm孔。

为验证方法的可行性 ，笔者直接选用两个PZT结验证是否可以算出方向交点，得到损伤位置。在实际应用中，由于损伤所在位置具有不确定性，例如损伤位置在PZT结附近或者PZT结的连线上，因此需采用3个及以上PZT结，通过计算每个PZT结接收到的不同损伤方向，并对最终得出的各损伤方向求交点，任意两个损伤方向的交点即为损伤位置。在布置各PZT时，考虑到各PZT坐标值将代入损伤方向算法公式中计算，为使计算精度更高，使得定位结果更加准确，各PZT的坐标值需更为精确，因此文中各PZT结均采用3个圆形PZT呈等边三角形布置。由于每个PZT的直径为10 mm，板尺寸较大，设置PZT间距为15 mm,且经实验研究表明PZT结中的压电片间距设为15 mm可行。以板的中心为坐标原点，建立直角坐标系，各PZT编号及7个PZT和孔的位置坐标如图4(b)所示。

2.2 采集响应信号并提取损伤散射信号

首先采集无损伤状态下的响应信号，对0号PZT施加激励信号，分别采集其他6个PZT接收到的Lamb波响应信号。为了消除外界环境对数据的影响，对每个频率的数据在同一结果状态下进行多次测量求平均值，并利用LabView软件中的有限冲击滤波器进行滤波，实验时对采集信号进行归一化处理，其中PZT3接收到的健康响应信号如图5所示。

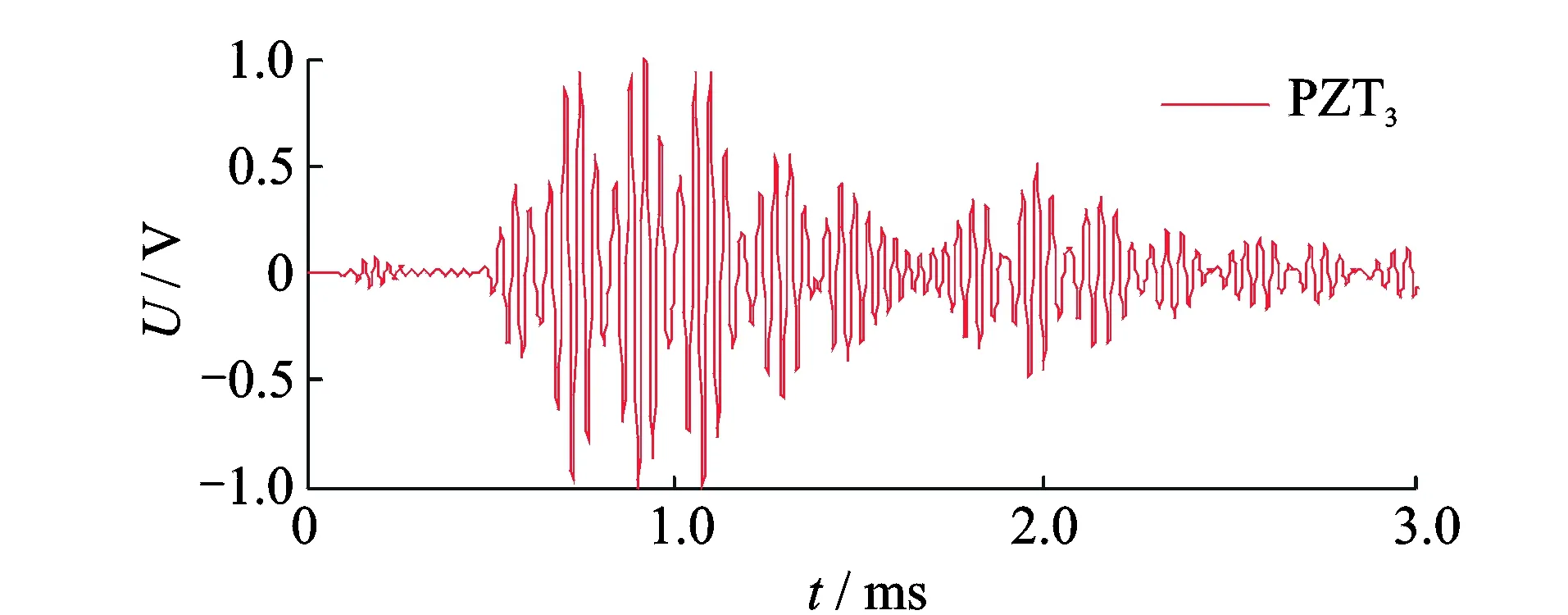
图5 PZT3采集的健康响应信号Fig.5 Health response signal collected by PZT3

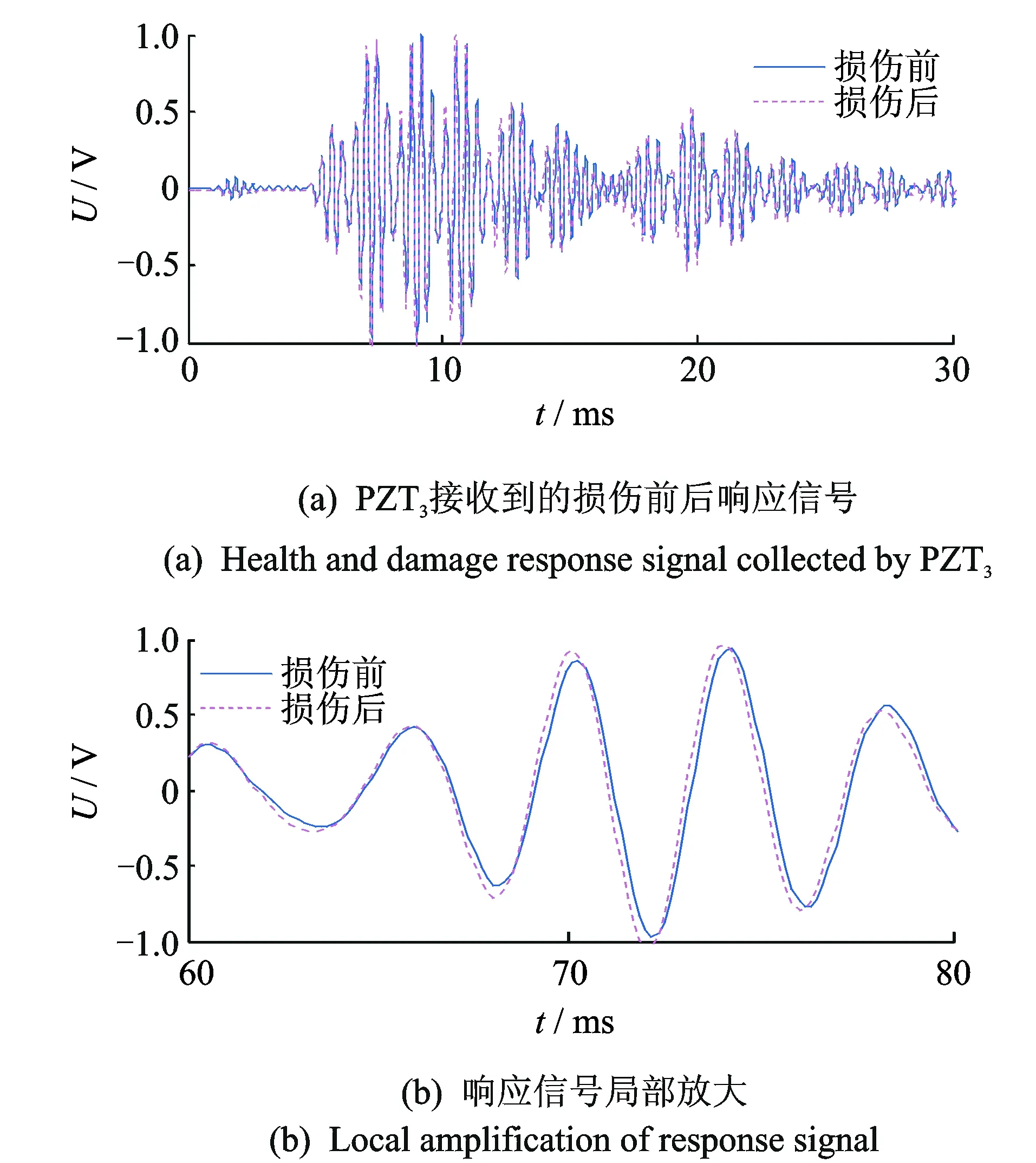
图6 PZT3损伤前后响应信号Fig.6 Health and damage response signal collected by PZT3 and local amplification

文中选用的损伤形式是在实验结构中形成一个通孔，损伤后信号采集时依然选择PZT0施加激励，现选择PZT3接收到的损伤后信号与其健康信号作对比分析，如图6所示。图6(a)为PZT3损伤前后响应信号，选取6×10-5至8×1005s时间段响应信号局部放大如图6(b)所示，可以看出，在损伤前、后信号差异并不十分明显，且幅值发生微弱变化。由于实验板的尺寸无法达到理论要求的无限大，Lamb波在板中传播一段距离后，波包的混叠现象增强，如果直接采用单纯的损伤前后信号相减的方法，并不能完全得到损伤信号。

根据互相关理论，响应信号由激励信号激发得到，因此响应信号与激励信号的相关程度最高，运用文中提出的方法，对损伤前后响应信号分别与激励信号进行互相关运算，并将相关运算后的信号做差，得到差信号，即得到损伤散射信号，对差信号的波包进行重构，便可提取到损伤散射信号波包的峰值到达时间。分别对6个PZT接收的损伤前后响应信号进行损伤散射信号提取，其中PZT3处理后的信号如图7所示，损伤散射信号能够被提取，且可得到完整波包。

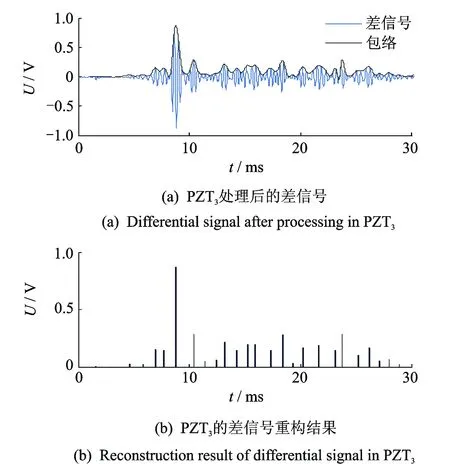
图7 用文中提出的方法得到的PZT3损伤散射信号结果Fig.7 Damage scattering signal results got by PZT3

2.3 求解Lamb波在板中传播速度与损伤方向

在无损状态下，将波形发生器与波形接收器直接相连，得到直连信号，再将波形发生器与激励压电片连接，同时6个PZT依次接收，得到Lamb波健康响应信号。由直连信号可得设备的延时为t0=8.16×10-6s。6个接收PZT得到的响应信号的第一个包络峰值的到达时间如表1所示。根据激励压电片与接收压电片在板中的位置，可求得PZT0与PZT1,…,PZT6的距离。由速度计算公式v=s/t可得Lamb波到达各PZT的传播速度，对各PZT结的各PZT速度求平均值，得到PZT结的速度。

由于各PZT的距离较近，其接收到的损伤散射信号时间间隔很短，速度差异引起的位移差异很小，相对于Lamb 波传播路径，各PZT接收到响应信号的方向偏差较小，因此考虑各PZT结的各个压电片接收到的Lamb波速度选为相同值，如表1所示。由于实验用复合材料板尺寸较小，板材对于损伤前后Lamb波波速影响差异较小，所以损伤前后Lamb波在板中速度取相同值。

根据提取到的损伤信号，对每个压电片接收到响应信号的差信号重构如图8所示，提取重构信号中第1个峰值到达时间，图8中坐标值x即为峰值到达时间，y为峰值。

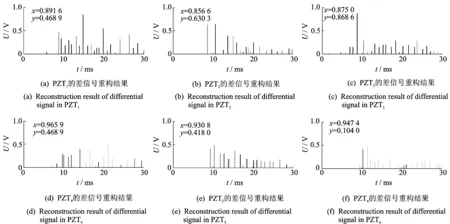
图8 各PZT损伤散射信号重构Fig.8 Reconstruction of damage scattering signals collected by each PZT

表1 Lamb波传播速度

由图中提取的各峰值坐标x值可以得出损伤信号到达2,5号PZT的时间最短，因此选取两个PZT结的2号和5号PZT为基准压电片。根据位置坐标，由损伤信号重构结果可得损伤波包到达各PZT的时间及波包传播距离提取如表2所示。将表2中得出的PZT1与PZT2的时间差和位移差、PZT2与PZT3的时间差和位移差、PZT4与PZT5的时间差和位移差、PZT5与PZT6的时间差和位移差带入式(5)得：k1=2.498 4/1.273 1，k2=1.639 7/-1.639 7，k3=-2.255 3/-1.373 8，k4=-1.875 2/1.875 2。对应角度分别为：α1=68.185 9°/51.850 9°,α2=58.622 3°/-58.622 3°,α3=-66.087 5°/-53.948 8°,α4=-61.930 1/61.930 1°。理论上，k1与k2相等，k3与k4相等，考虑到实验过程中存在误差，选取近似相等的角度数据，α1=51.850 9°，α2=58.622 3°，α3=-66.087 5°，α4=-61.930 1°。分别取2者平均值，可得PZT结1的损伤方向θ1=34.763 4°，PZT结2求得损伤方向θ2=25.991 2°，损伤位置坐标为(-7.37，-121.77)，实际损伤位置为(0,-125)，误差为8.05 mm，其中误差值为本文提出方法计算得损伤位置与实际损伤位置的距离。

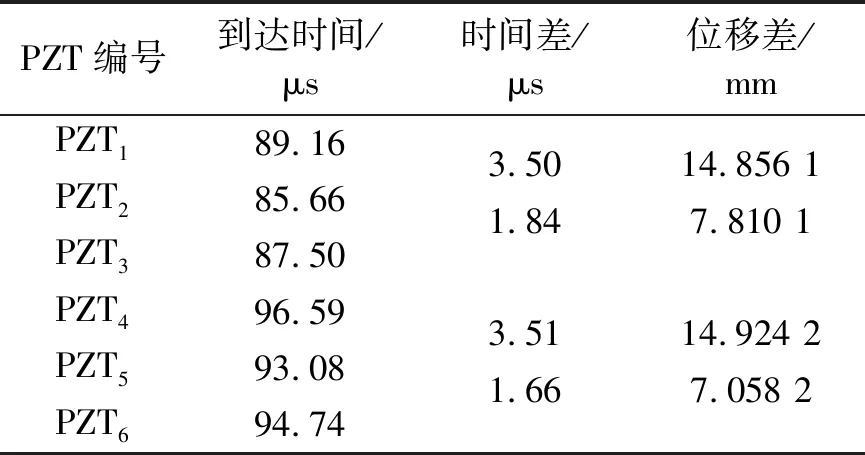
表2 损伤散射信号波包到达时间

3 结束语

利用MATLAB 软件编写了基于互相关理论的信号处理方法，在激励频率300 kHz的条件下，对实验测得的信号数据进行处理，根据处理后结构健康响应信号与结构损伤响应信号的差异，用本方法能够提取出损伤散射信号，且对散射信号重构后可以得到损伤散射信号各波包峰值对应的时间；

根据PZT结在板中的位置，并选择2,5号PZT为基准PZT，将各PZT坐标代入损伤方向计算公式结损伤判定方法利用损伤方向算法得到了各PZT结接收到的经由损伤孔散射的其中一个Lamb波方向，且方向交点确定的损伤位置与实际损伤位置距离为8.05 mm，误差在可接受范围内。

今后将进一步研究多损伤问题，针对多损伤的多方向性，考虑到多损伤问题信号处理的复杂性，对Lamb波在碳纤维增强树脂基复合材料中的传播速度以及信号处理方法进行优化，从而提取出多损伤散射信号的多个损伤包络的到达时间，实现多损伤定位。同时，对PZT结的最大间距进行讨论，得到PZT间距的范围，改进损伤方向算法，从而进一步完善损伤定位方法。