VMD多尺度熵用于高速列车横向减振器故障诊断*

苟先太， 李昌喜， 金炜东

(西南交通大学电气工程学院 成都，610031)

引 言

高速列车横向减振器属于典型的非线性复杂系统，列车运行时产生的振动信号具有明显的非线性、非平稳特征，故障诊断时采用传统的信号处理方法很难提取到故障的有效特征[1]。针对该问题，不少学者进行了研究。文献[2]提出了基于聚合经验模态分解(ensemble empirical mode decomposition，简称EEMD)排列熵的特征分析方法，能有效解决模态混叠和端点效应。文献[3]提出了一种基于Copula函数的特征提取方法，将信号进行EEMD分解，对本征模态函数(intrinsic mode functions，简称IMFs)使用Gaussian Copula函数构建它们的联合概率密度函数,提取边缘分布的Kullback-Leibler Distance值，联合概率密度函数的均值和方差作为特征。EEMD是在经验模态分解 (empirical mode decomposition，简称EMD)的基础上的改进算法，能有效抑制模态混叠现象，但算法效率低。文献[4]提出的变分模态分解(variational mode decomposition，简称VMD)可以自适应地将振动信号分解成一系列有限带宽的模态函数集合，实现了各信号分量频率的分离，克服了EMD存在的模态混叠和数学理论缺乏等问题，并且算法效率高。

熵是一种度量时间序列复杂性的方法。从近似熵(approximate entropy，简称ApEn)[5]到样本熵(sample entrop，简称SpEn)[6]都是度量序列复杂度的方法。ApEn是将数据与其本身进行比较，由于熵测度的是新信息产生率，所以与其自身比较毫无意义。SpEn是改进的复杂性测度方法，具有较好鲁棒性，由于其测度信号单一尺度的复杂度，所以不能充分表征信号在不同尺度上的复杂程度[7]。文献[8]提出了多尺度熵(multiscale entropy，简称MSE)分析方法，即在多尺度上挖掘信号的SpEn，既可以从总体上量化序列的复杂度，又可以从多个尺度上提取有效特征，从不同角度准确识别信号。以MSE作为特征的提取方法常被应用到故障诊断及医学信号识别等领域。文献[9]提出了结合局部均值分解和MSE的特征提取方法，首先对原始振动信号进行改进的局部均值分解，然后利用MSE对分解结果进行量化，构成特征向量进行识别。文献[10]提出一种基于EMD的MSE的脑电信号瞬态特征提取方法，分类效果良好。

针对高速列车横向减振器故障振动信号的特点，笔者结合VMD和MSE的优点，用于高速列车横向减振器故障振动信号的特征提取，即VMD-MSE。实验结果表明，该方法可有效提取故障特征信息，实现故障类型的准确判断。

1 变分模态分解

VMD可以非递归地将振动信号分解成一系列有限带宽的固有模态函数，从而能够自适应地实现信号频域的有效分离。

1.1 变分问题的构造

VMD将一个原始信号f分解成k个模态函数uk(t)，每一个模态函数具有中心频率ωk。VMD可以表述为求解k个模态函数，使所有模态函数的带宽总和最小，约束条件是所有模态函数和等于原始信号f

(1)

具体步骤如下：

1) 通过对原始信号f的每个模态函数e-jωkt进行Hilbert变换，得到其单边频谱；

2) 对各模态函数e-jωkt混合预估中心频率e-jωkt，并将每个模态函数的频谱调制到相应的基带；

3) 求解解调信号梯度的平方L2范数，估计出每个模态函数的带宽。

1.2 变分问题的求解

通过引入拉格朗日乘子λ(t)和二次惩罚因子α，将约束变分问题变为非约束变分问题。其中α保证信号在高斯噪声存在情况下的重构精度，λ(t)使得变分问题的求解保持严格的约束性。延伸后的拉格朗日表达式如下

L({uk},{ωk},λ):=

(2)

(3)

(4)

(5)

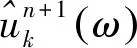
具体流程如图1所示。VMD算法的求解过程中，各模态分量不断更新其中心频率及带宽，最终可根据原始信号的频域特性完成频带的剖析，实现信号的自适应分解。

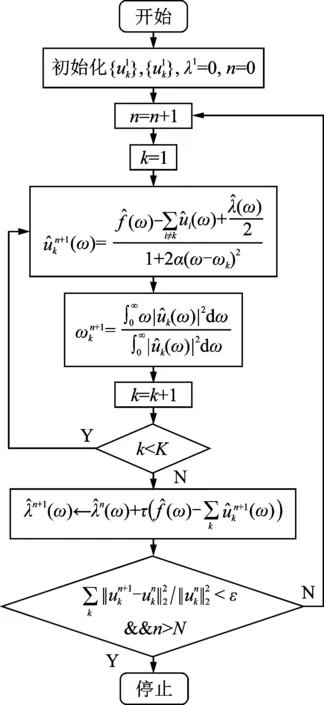
图1 VMD流程图Fig.1 Flowchart of VMD

2 故障诊断流程

高速列车横向减振器故障振动信号是典型的非线性、非平稳信号，故障特征主要体现在低频部分[11]。首先，采用小波包方法对原始振动信号处理；其次，用VMD方法分解得到具有特定物理含义的IMFs，以MSE方法对得到的IMFs进行定量描述，形成特征向量；最后利用一种基于Murphy改进的D-S方法作为融合规则的多准则特征评价方法对特征向量进行综合评价，去除冗余特征[12]，利用分类器实现高速列车横向减振器故障类型的识别。图2为高速列车横向减振器故障诊断具体实现步骤。

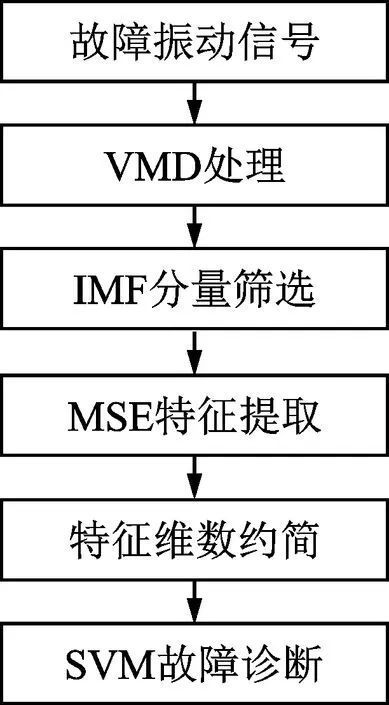
图2 故障诊断步骤图Fig.2 Graphic of the steps of fault diagnosis

3 高速列车横向减振器故障诊断

3.1 实验数据

实验数据是由西南交通大学牵引动力国家重点实验室提出的基于多体动力学软件Simpack建立的某动车组车辆系统非线性动力学模型仿真得到。模型结构如图3所示。其中:①表示构架1右侧上抗蛇行减振器；②表示构架1右侧下抗蛇行减振器；③表示构架1右侧横向减振器；④表示构架1空气弹簧；⑤表示构架2左侧横向减振器；⑥表示构架2左侧上抗蛇行减振器；⑦表示构架2左侧下抗蛇行减振器。横向减振器7种故障工况如表1所示。实验数据是在220 km/h下运行约3.5 min得到，采样频率为243 Hz。仿真实验的振动信号主要包括车体、一系、二系、构架、轮对各部位横向、纵向和垂向的振动位移和车体、构架、轴箱上各个部位三个方向的振动加速度，共58个通道数据。

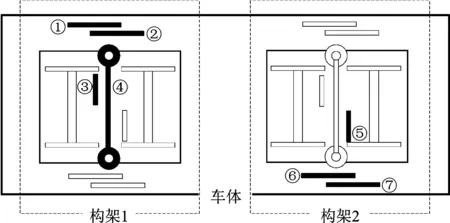
图3 模型结构图Fig.3 Structure diagram of the model

图4为构架1架1位横向加速度振动信号7种工况部分数据时域和频谱图。由图4可以看出，故障状态振动信号时域图和频谱与原车有明显的区别，但不同故障状态的振动信号时域图和频谱相似，无法识别。

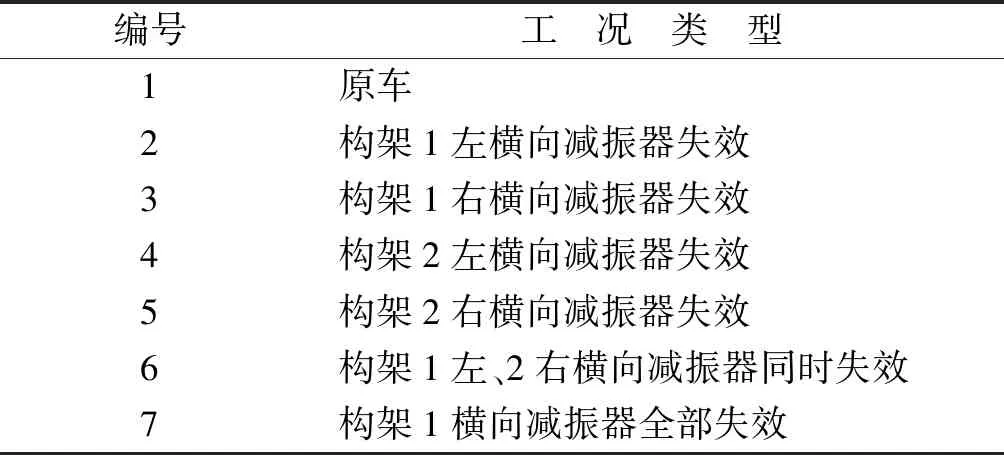
表1 7种工况编号

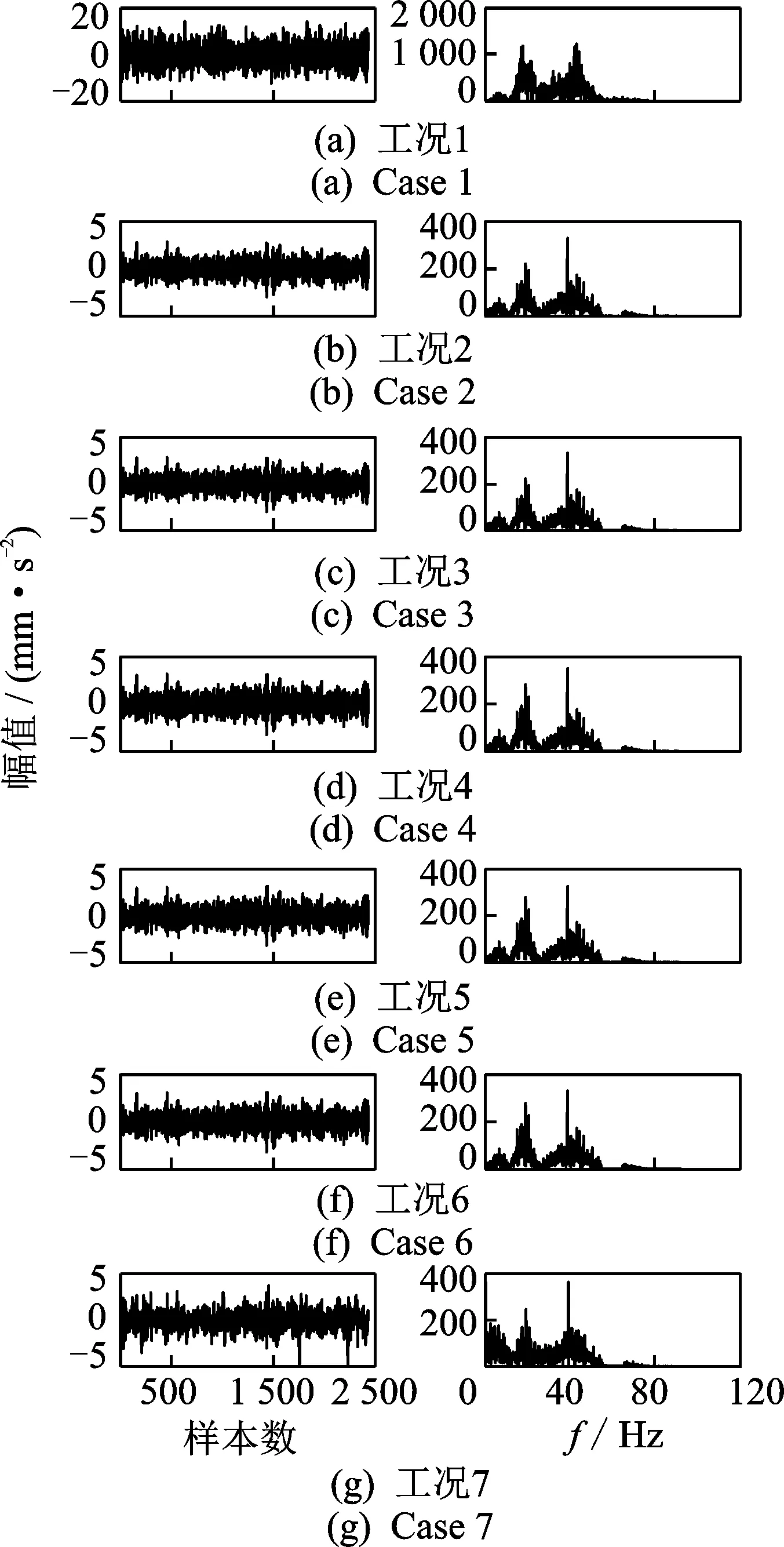
图4 7种工况的时域信号和频谱图Fig.4 Time-domain signal and spectrum graphics of seven working condition

3.2 振动信号的变分模态分解

对信号进行VMD分解，首先要确定分解层数K。K取值过小时，VMD分解会出现模态混叠或者模态丢失的现象；反之分解结果出现残余分量。文中采用观察模态频谱图的方法确定K。选用构架2架8位横向加速度信号进行VMD分解，信号采样频率243 Hz，选取486个数据点作为1个样本。图5(a～c)为振动信号在不同K值下VMD的分解结。其中平衡约束参数α=30，τ=0以保证实际信号的保真度。

从图5(a～c)中可以看出，K=8时IMF8的频谱中存在不同尺度信息，模态分解不充分；K=10时IMF7和IMF8两个模态的频谱几乎重合，存在多余的模态分量。因此，选取K=9。为了验证本方法的优势，利用EMD和EEMD方法对上述仿真信号进行处理，以作对比。分解结果如图6所示。从图6(a)中可以看出，EMD处理后信号存在严重的模态混叠，而图6(b)中EEMD处理后的IMF3～7分解充分，而包含相对高频段信息的IMF1和IMF2存在模态混叠。

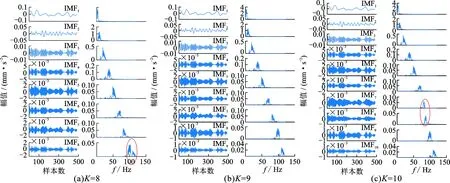
图5 不同K值VMD处理结果Fig.5 Processing results by VMD under different K

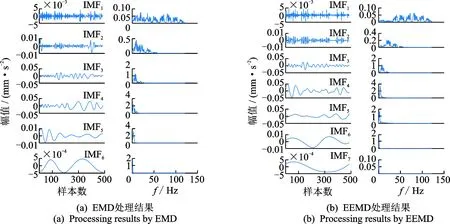
图6 基于EMD和EEMD的振动信号处理结果Fig.6 Processing results of vibration signal by EMD and EEMD

为了说明本方法的计算效率，采用不同方法对同一工况的同一通道数据所有样本进行分解，需要的时间如表2所示。EMD方法效率最高，VMD次之，EEMD方法的效率最低。理论上，每个IMF都是一个平稳信号，代表原信号中的特征成分之一。由于受参数选取等因素影响，分解结果中不可避免地存在虚假成分。文献[13]提出了基于互信息的HHT虚假分量识别方法，研究结果表明，与相关系数法相比，互信息法能更好的识别虚假分量。同时通过各方法分解出的IMF数来确定有效IMF数，因此文中采用互信息法选取VMD和EEMD方法的前4个有效IMF，EMD方法的前3个有效IMF。

表2 不同方法的分解效率

3.3 多尺度熵特征提取

在MSE的计算中，参数的选择会影响计算结果。其相似容限r取值一般与原始序列的标准差相关(一般取r=0.1-0.25SD，SD为原始序列标准差)，因此反映的是原始序列在不同尺度上的复杂度。此外对于嵌入维数m，研究表明当m=2时，计算结果的准确性与序列的长度N依赖性最小。尺度因子τ=τmax。

实验中每种工况数据是在200 km/h运行210 s得到，采样频率为243 Hz。截取486个采样点作为1个样本，除去异常点，每种工况90个样本。由于列车运动状态需要多个自由度表示且多通道数据具有较强的相关性，所以在特征提取时对7～18通道采用串联的方式进行数据融合，则有

F(xi)= [f1(c7),f2(c7),…,fn(c7),f1(cj),

f2(cj),…,fn(cj),…,f1(c18),f2(c18),…,

fn(c18)] (1≤i≤90,7≤j≤18)

(6)

其中：xi为第i样本；cj为第j通道;n为有效模态数;fn(cj)=MSEIMFn为通道j数据模态分解后第n个有效模态的多尺度熵；F(xi)为xi的多尺度熵。

可知，VMD和EEMD方法得到的特征为90*(12*4)的矩阵，EMD方法得到的特征为90*(12*3)矩阵。

3.4 特征约简和支持向量机故障识别

通过VMD-MSE方法得到特征向量，采用文献[12]的特征评价方法进行特征评价，最后得到一个特征排序列表。根据每一维特征量的重要性对该表依次去掉冗余特征，得到若干个嵌套的特征子集F1⊂F2⊂…⊂F来训练SVM，并以SVM的预测准确率评估特征子集的优劣，从而获得最优特征子集。7种工况各90个样本集经归一化后，随机选取50个作为训练样本，40个样本作为测试样本。支持向量机故障识别时，输入的特征维数大于等于3，图7为不同方法的不同特征子集的分类精度。

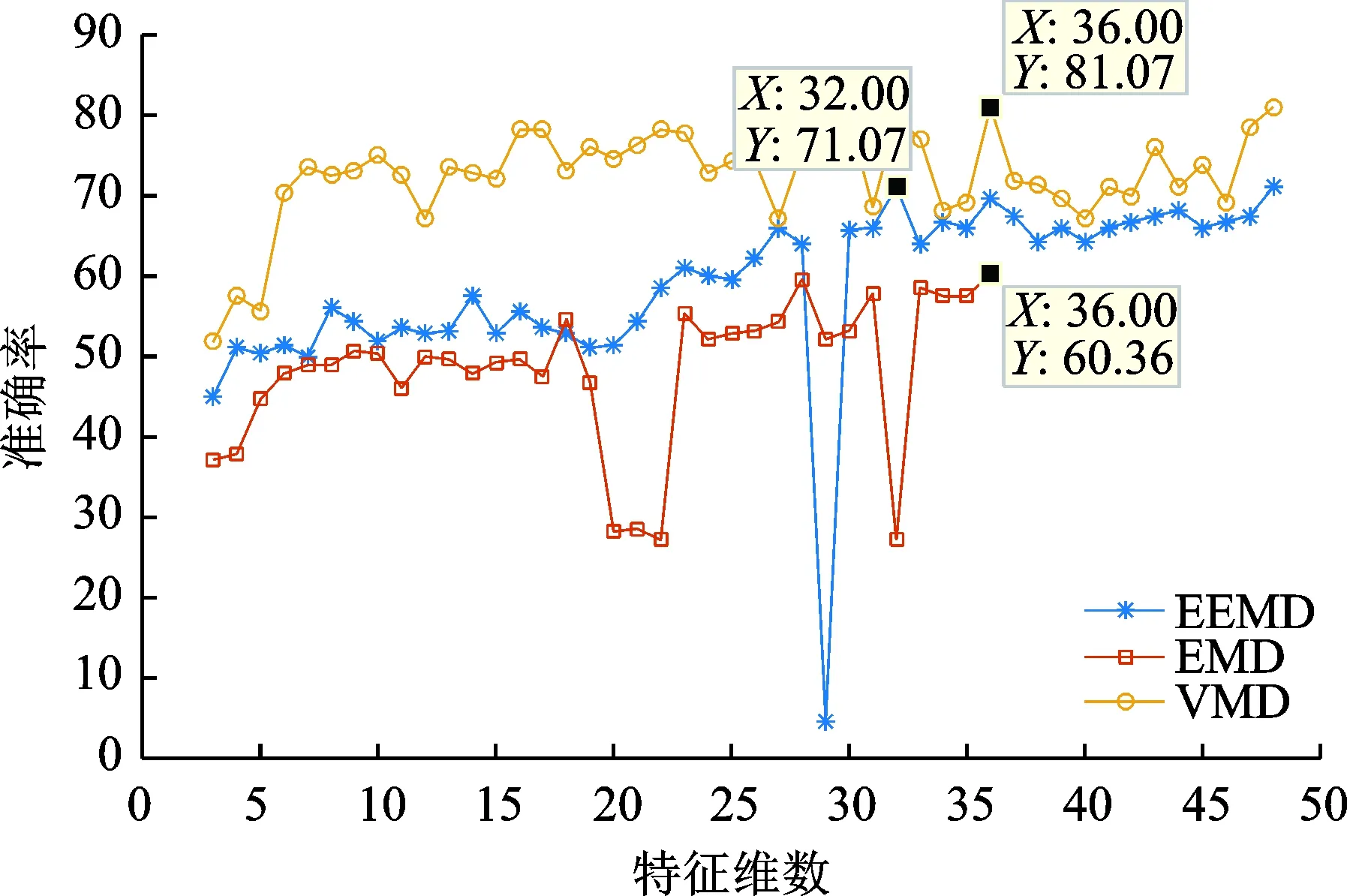
图7 不同特征子集故障识别率Fig.7 Fault recognition rate of different feature subsets

从图7中可以看出，基于VMD-MSE方法得到的特征向量的故障识别率高于基于EMD-MSE和EEMD-MSE方法得到的特征向量的识别率，并且在特征子集维数达到6后趋于稳定。EMD-MSE和EEMD-MSE方法的特征向量的准确率都有巨大波动，验证了VMD-MSE方法在特征提取时的优越性。另外，EMD方法的最优特征子集维数是28，EEMD方法的最优特征子集维数是32，VMD方法的最优特征子集维数是36。

表3～5为各方法最优特征子集准确率的混淆矩阵。由表3～5可知，在针对高速列车横向减振器故障信号的特征提取中，VMD-MSE方法比EMD-MSE方法具有更好的识别效果。EEMD和VMD对原车状态和多个横向减振器失效工况的识别率最高可达100%，对于多个横向减振器失效工况的故障检测具有很高的可行性，但对单个横向减振器失效的故障识别率较低。这是因为同一架构上的两个横向减振器安装位置比较接近，任何一个失效对于列车振动的影响差异不大，导致难以区分同一架构上的横向减振器失效的具体位置。如果将同一架构上的两个横向减振器归为一类，则故障识别率大大提高。这也间接说明多个横向减振器失效对车体的影响大于单个横向减振器失效对车体的影响。

表3 EMD-MSE特征提取方法识别结果

Tab.3 Identification of feature extraction Method by EMD-MSE

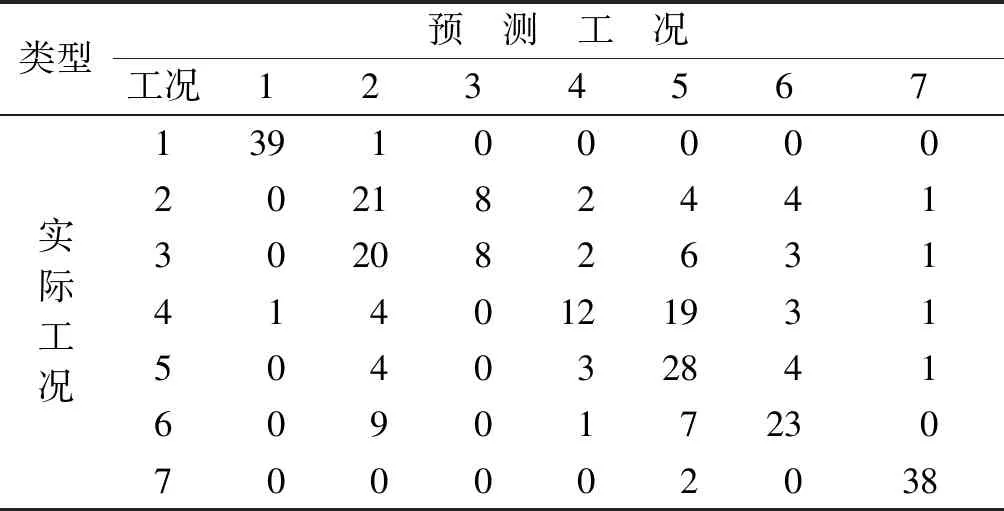
类型预 测 工 况工况1234567实际工况1391000002021824413020826314140121931504032841609017230700002038

表4 EEMD-MSE特征提取方法的识别结果

Tab.4 Identification of feature extraction Method by EEMD-MSE

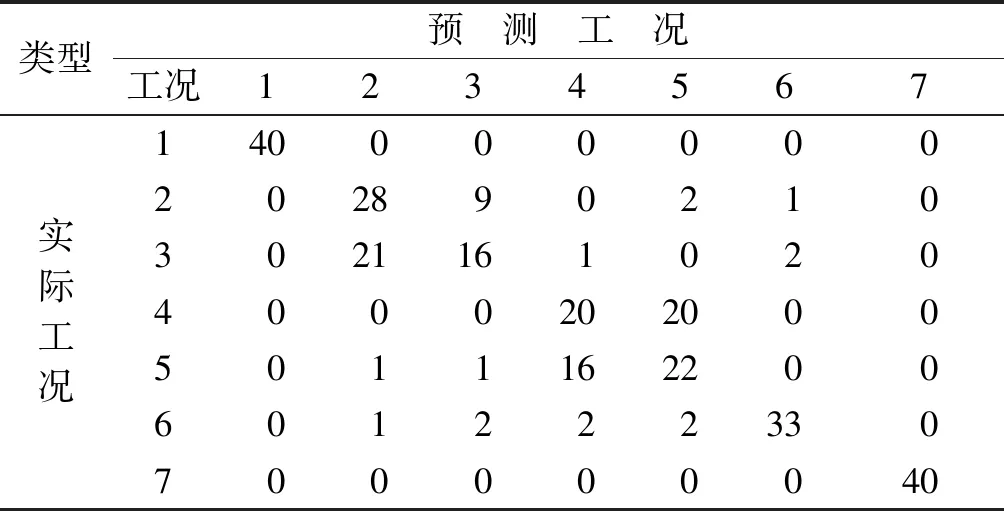
类型预 测 工 况工况1234567实际工况140000000202890210302116102040002020005011162200601222330700000040

表5 VMD-MSE特征提取方法的识别结果

Tab.5 Identification of feature extraction Method by VMD-MSE

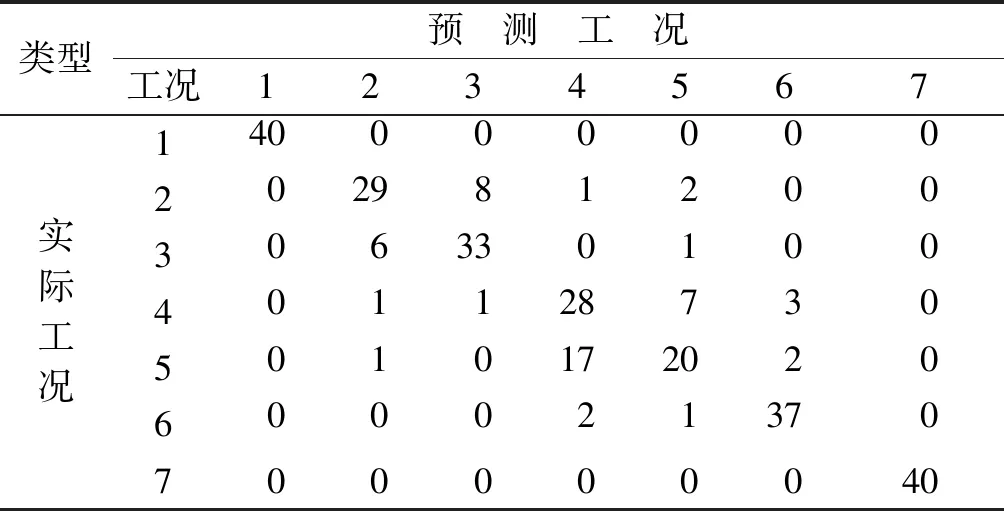
类型预 测 工 况工况1234567实际工况1400000002029812003063301004011287305010172020600021370700000040

4 结束语

笔者把VMD和MSE相结合的特征提取方法应用于高速列车横向减振器的故障诊断，实验结果表明，该方法得到的特征向量可以有效识别故障类型。基于VMD-MSE的特征提取方法得到的特征向量相比其他两种方法有较好的分类结果，而且相对稳定。同时该方法的计算效率高。基于离线数据的高速列车横向减振器故障诊断是对高速列车安全状态实时监测的预演，对后期实时在线分析与评估具有重要意义。