基于叶片贡献度的叶盘系统频率转向特性*

张宏远， 袁惠群， 杨文军， 赵天宇

(1.沈阳理工大学汽车与交通学院 沈阳，110159) (2.东北大学机械工程与自动化学院 沈阳，110819) (3.东北大学理学院 沈阳，110819)

引 言

航空发动机压气机谐调叶盘具有频率转向现象[1-2]，而加工误差、工作过程中的磨损和抑制颤振等原因会导致各叶片的固有频率的差异，即失谐。失谐会造成严重的局部化[3]。

国内外研究人员对于失谐叶盘系统频率转向特性开展了大量研究。文献[4-5] 对叶盘频率与系统参数的关系进行了研究。文献[6-9] 研究了叶盘频率转向与失谐之间的关系。文献[10-13]对叶片频率转向与振型转换特性进行了研究。王南飞等[14]的研究表明旋转叶片必须考虑预应力影响。上述研究没有考虑在频率转向区域叶片对叶盘系统振动局部化的贡献度。

笔者采用子结构模态综合法，考虑了预应力效应对叶盘系统有限元缩减模型的影响，分析谐调叶盘系统的频率转向特性和应变能分布，提出贡献度因子来衡量叶片和轮盘对失谐叶盘系统局部化的影响，通过计算不同转向间隙对应的贡献度因子，分析叶片对失谐叶盘系统振动局部化的贡献度。

1 叶盘系统建模

航空发动机叶盘系统如采用整体模型将花费大量计算时间，若再考虑榫头与榫槽的非线性接触会使分析极为困难。由于失谐不能采用循环对称模型，因此采用子结构模态综合法[15-17]，共划分38个子结构，叶片网格采用solid45单元, 轮盘网格采用solid187单元，每个子结构共有52 163个单元和79174个节点。叶片的密度为4 400 kg/m3，弹性模量为113 GPa，泊松比为0.3；轮盘的密度为4 700 kg/m3，弹性模量为150 GPa，泊松比为0.3。压气机叶盘系统子结构缩减模型如图1所示。

图1 叶盘系统子结构缩减模型Fig.1 Finite element model of a bladed disk

第i个叶盘子结构的强迫振动方程可表达为

(1)

其中:Mi，Ki，qi,Fi分别为第i个子结构的质量、刚度、位移和子结构的作用力矩阵。

航空发动机等旋转机械旋转部件是否考虑离心力的影响对计算结果有较大的影响，因此，考虑预应力的方程为

(2)

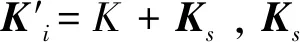
(3)

令子结构界面固定，可得

(4)

由式(4)求得正则化模态φ1, 即

φ1=[φlφh]

其中：φl和φh分别为低阶和高阶模态。

φ1满足以下条件

其中：E为单位矩阵。

由于在分析叶盘系统的振动模态时主要关注低阶模态，所以选取低阶的模态φl构成主模态φm，即

φm=φl

(7)

当忽略惯性项并只考虑界面自由度的作用力，由方程(3)得：

(8)

令 {qm}=E,{qs}=φJ

约束模态

(9)

第i个子结构的Ritz基向量为

(10)

坐标变换方程为

(11)

其中：p为子结构模态坐标；φi为坐标变换矩阵[15]。

用式(11)将式(2)转换到模态坐标系

(12)

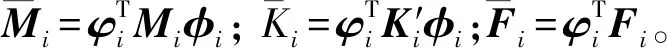
采用文献[18]的方法缩减自由度，令

(13)

(14)

(15)

其中：pa为ps缩减后的模态坐标。

式(12)可以转换为

P=βX

(16)

叶盘系统自由度进行缩减后的强迫振动方程为

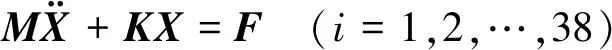
(17)

表1列出了叶片在不同模态截断数下的部分无量纲动频。通过对比可知，模态截断数的取值显著影响计算精度，当模态截断数Tn<20时，精度较差；当模态截断数Tn≥20时，精度较好，模态截断数的增加对精度影响较小。

2 谐调叶盘系统模态振型转换特性

2.1 谐调叶盘系统的频率转向区域

通过对叶盘系统模态分析，将获得的频率除以某一频率值进行无量纲化，将无量纲固有频率按照节径排列，可以大致分成4个模态族，如图2所示。图中的模态族Ⅱ和模态族Ⅲ的0～6节径构成了谐调叶盘系统的频率转向区域。图中所涉及的频率和应变能等都除以某一频率值无量纲化。

由图2可知模态族Ⅰ的频率都集中在1.0附近，由图3可知模态族Ⅰ的大部分应变能在叶片上，节径的变化对叶盘的频率基本没有影响，在该模态族为叶片模态；由图2和图3可知,在模态族Ⅱ的0～6节径叶盘的振动能量大部分在轮盘上，节径的变化对叶盘的振动影响显著，模态族Ⅱ为轮盘模态；同理可知，模态族Ⅲ的0～6节径为叶片模态。

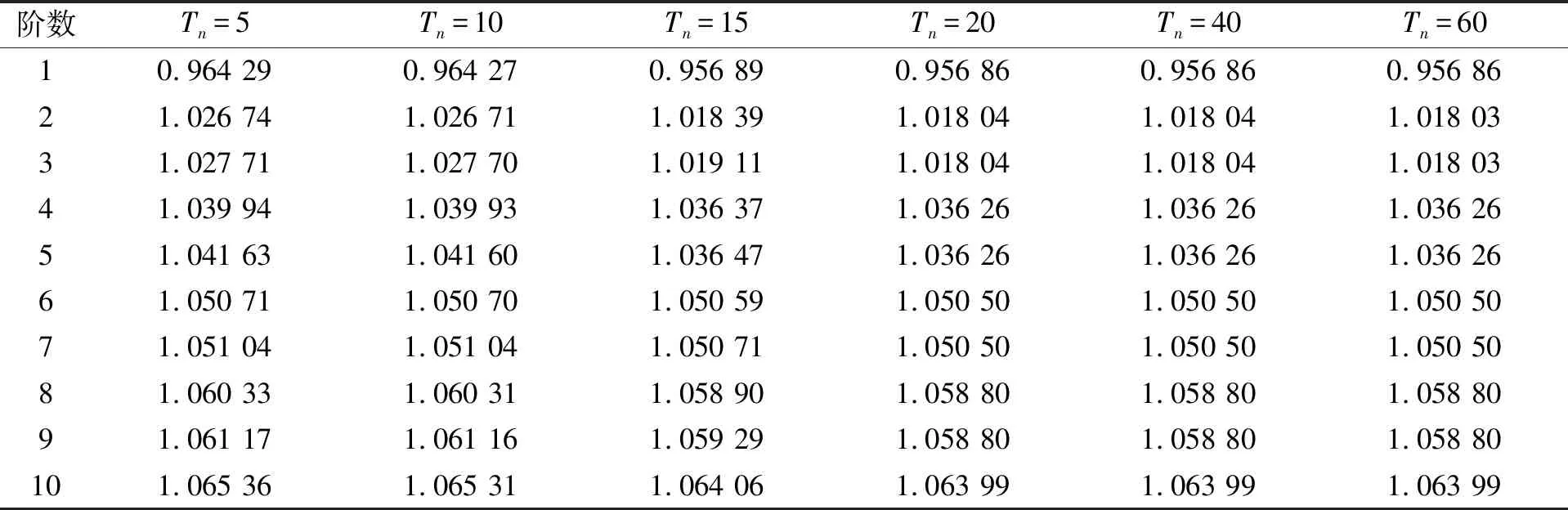
表1 不同模态截断数下叶片无量纲动频

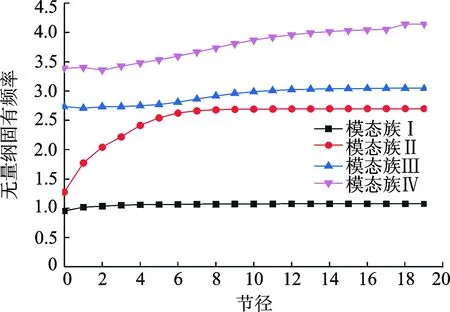
图2 谐调叶盘系统频率转向特性Fig.2 The frequency steering characteristics of the tuned bladed disk system

图4为模态族Ⅱ在频率转向区域的振动特性，选择节径数为1～7和激励阶次为1～6时叶盘系统应变能分布。从图4可知:在频率转向区域(0～6节径)，应变能随着节径数的增大而增大，在节径数为6时达到最大，当超过频率转向区域，即节径数为7时，叶盘系统的应变能大幅度降低；在同一节径数下，当节径数与激励阶次相同时叶盘系统的应变能最大，比如图中当节径为3、激励阶次为3时的应变能，这一结论符合三重点原理[19]；当激励阶次和节径数同为6时谐调叶盘系统的应变能最大。

图3 各模态族叶片应变能Fig.3 Strain energy of modal families

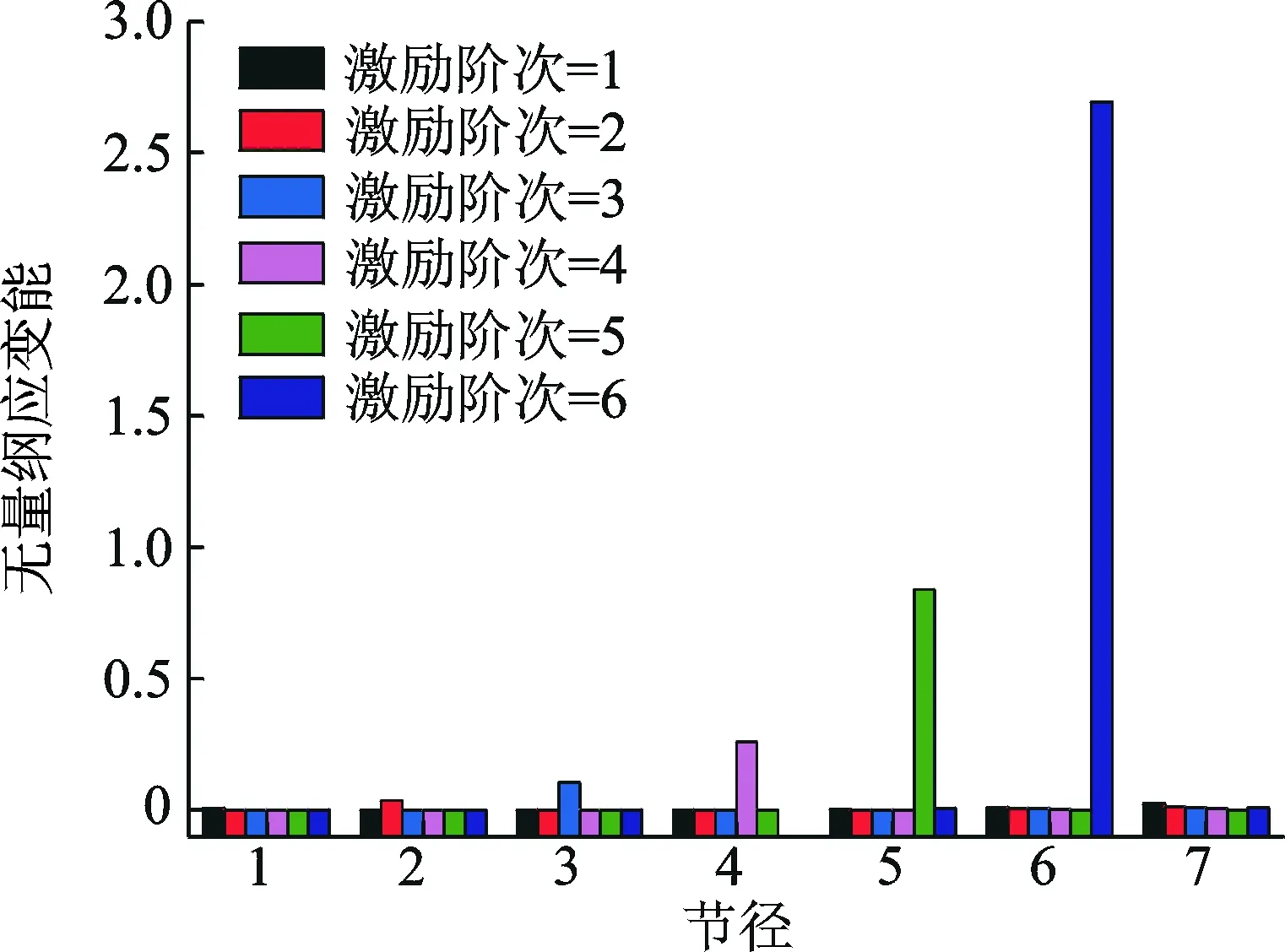
图4 模态族Ⅱ在频率转向区域应变能分布Fig.4 Strain energy of modal family Ⅱ in the region of frequency veering

2.2 频率转向间隙

在频率转向区域，节径数的变化显著影响叶盘系统模态振动局部化。为了分析相邻模态族叶片应变能对叶盘系统振动的贡献度，引入了频率转向间隙[10]，相对频率间隙d计算公式为

(18)

其中：f1，f2和p分别为模态族Ⅰ的无量纲频率、模态族Ⅱ的无量纲频率及对应的节径；f1min和f2max分别为模态族Ⅰ最小无量纲频率和模态族Ⅱ的最大无量纲频率。

采用式(18)以模态族Ⅱ和模态族Ⅲ为例，计算了相邻两个模态族在频率转向区域的频率转向间隙，计算结果如表2所示。

表2 模态族Ⅱ和模态族Ⅲ频率转向间隙

Tab.2 The frequency veering distance of modal family Ⅱ and Ⅲ

节径模态族Ⅱ无量纲频率模态族Ⅲ无量纲频率无量纲频率转向间隙01.2782.7360.82411.7762.7080.52522.0422.7330.33832.2192.7360.23342.4142.7500.13952.5442.7710.08962.6242.8100.07172.6632.8650.07682.6802.9180.08992.6892.9600.101102.6932.9890.110112.6963.0090.116122.6973.0230.121132.6983.0320.124142.6993.0380.126152.6993.0420.127162.6993.0440.128172.7003.0460.128182.7003.0470.129192.7003.0470.129

由表2可知，随着节径数的增加，频率转向间隙呈现先减小再增加的趋势。频率转向间隙在6节径时达到最小，最小值为0.071，在频率转向区域(0～6节径)频率转向间隙数值变化非常明显，在远离频率转向区域(9～19节径)，频率转向间隙基本保持不变。

3 叶片对失谐叶盘系统振动局部化贡献度

3.1 贡献度因子

从谐调叶盘系统模态振型转换特性可知，在频率转向区域，叶盘系统的振幅和应变能随着节径数的变化呈现一定的规律性，为了评价在频率转向区域叶片和轮盘对失谐叶盘系统振动局部化的影响，从模态应变能角度定义了式(19)的贡献度因子。

叶片贡献度因子

(19)

其中：Cb为叶片贡献度因子；Eb i为第i个扇区叶片应变能；Ed i为第i个扇区轮盘应变能。

3.2 失谐叶盘系统模态振动局部化贡献度

叶片刚度失谐后会使叶盘系统模态振型出现较大改变，各叶片的振动能量也不同，当较大的振动能量集中在几个叶片上时就会导致模态振动局部化现象。为了定量描述叶盘系统振动局部化程度，引入了文献[10]定义的局部化因子，该局部化因子的定义如式(20)所示。由于文中叶片刚度失谐模拟采用叶片弹性模量失谐来实现，三种失谐模式是通过实验测得的三组叶片静频，然后采用二分法和有限元分析来识别失谐参数，通过反复迭代计算，最终获得与实验测得的叶片静频对应的弹性模量值。通过计算三种失谐模式下叶盘系统在频率转向区域的局部化因子，获得如图5所示的局部化因子随激励频率的变化情况。

(20)

从图5可知，随着激励频率的增大，叶盘系统的局部化因子开始变化较小，然后逐渐增大。当激励频率为2.6时，模态族Ⅱ和模态族Ⅲ的频率转向间隙为最小，失谐叶盘系统振动局部化显著，导致在该处振动局部化因子急剧增加。

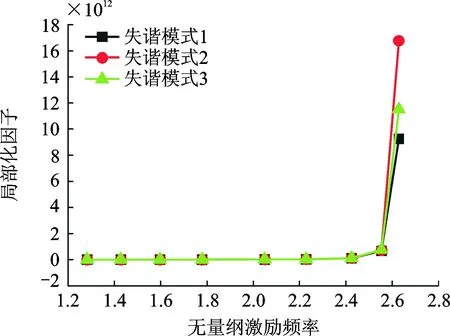
图5 激励频率对失谐叶盘系统模态振动局部化影响Fig.5 Effect of excitation frequency on the mode vibration localization of the mistuned bladed disk system

3.3 失谐叶盘系统受迫振动响应局部化贡献度

在频率转向区域，对失谐叶盘系统进行受迫振动分析，计算三种失谐模式下频率转向间隙对应模态族Ⅱ的叶片贡献度因子和局部化因子，频率转向间隙(无量纲)对失谐叶盘系统振动受迫响应贡献度如图6所示。

图6 频率转向间隙对失谐叶盘系统振动响应贡献度影响Fig.6 Effect of frequency veering distance on the contribution degree of forced vibration response

从图6可知，随着频率转向间隙的增大，叶片贡献度因子逐渐减小，在最小频率转向间隙处三种失谐模式的叶片贡献度因子最小，其中失谐模式2的叶片贡献度因子最小。图7分析了叶片贡献度因子与叶盘系统局部化因子的关系，从图上可知，随着叶片贡献度因子的增大，局部化因子增大，叶盘系统局部化程度逐渐增加。

图7 叶片贡献度对失谐叶盘系统振动响应局部化影响Fig.7 Effect of the contribution degree on the localization of forced vibration response

4 结束语

基于航空发动机压气机叶盘系统建立了有限元模型，进行了模态分析和受迫振动响应分析，通过计算频率转向间隙、贡献度因子和局部化因子，从应变能角度研究了在频率转向区域谐调和失谐叶盘系统振动特性；分析了谐调叶盘系统模态振型转换特性，找到了频率转向区域，在模态族Ⅱ和模态族Ⅲ发生了频率转向现象；在频率转向区域叶盘系统的应变能随节径和激励阶次的变化而变化，在激励阶次6和节径数为6时应变能最大；定义了贡献度因子，通过计算贡献度因子分析了失谐叶盘系统模态振动局部化贡献度；通过计算局部化因子，分析了失谐叶盘系统受迫振动响应，在频率转向区域叶片贡献度因子和局部化因子呈现一定的规律性。