Control of the common rail pressure in gasoline engines through an extended state observer based MPC

Chao WU, Kang SONG, Hui XIEState Key Laboratory of Engines,Tianjin University,Tianjin 300072,China

Abstract In this paper, a model predictive control (MPC) solution, assisted by extended state observer (ESO), is proposed for the common rail pressure control in gasoline engines. The rail pressure dynamic, nonlinear with large uncertainty, is modeled as a simple first order system. The discrepancy of the model from the real plant is lumped as “total disturbance”, to be estimated in real-time by ESO and then mitigated in the nonlinear MPC,assuming the total disturbance does not change in the prediction horizon.The nonlinear MPC problem is solved using the Newton/generalized minimum residual(GMRES)algorithm.The proposed ESO-MPC solution,is compared with the conventional proportional-integral-differential(PID)controller,based on the high-fidelity model provided in the benchmark problem in IFAC-E-CoSM. Results show the following benefits from using ESO-MPC relative to PID (benchmark): 1) the disturbance rejection capability to fuel inject pulse step is improved by 12% in terms of recovery time; 2) the transient response of rail pressure is improved by 5% in terms of the integrated absolute tracking error; and 3) the robustness is improved without need for gain scheduling,which is required in PID.Additionally,increasing the bandwidth of ESO allows reducing the complexity of the model implemented in MPC, while maintaining the disturbance rejection performance at the cost of high noise-sensitivity.Therefore,the ESO-MPC combination offers a simpler and more practical solution for common rail pressure control,relative to the standard MPC,which is consistent with the findings in simulation.

Keywords: Rail pressure control,fuel system control,model predictive control,extended state observer,active disturbance rejection control

1 Introduction

Common rail fuel system has become norm in modern diesel engines, and is becoming more and more popular in gasoline engines,in the face of the stringent emission legislations[1]. The common rail pressure affects the fuel amount delivered into the cylinder, the penetration rate of the fuel spray,and the fuel air mixture preparation[2].Therefore,the rail pressure control plays a fundamental role in improving the combustion process, the engine thermal efficiency, and emissions [2].This drives the need for the accurate rail pressure control with fast transient response and high disturbance rejection capability.

The dynamic of the rail pressure is, however, highly nonlinear with a large amount of uncertainties. For instance,the fuel flow rate into the common rail is affected by the pressure in the common rail,the pressure in the high pressure (HP) fuel pump, the engine speed, and the HP fuel pump solenoid position [3]. The pressure in the HP fuel pump is, unfortunately, unmeasurable.In addition,disturbances,such as the fuel injection rate variation and the pressure fluctuation at the HP fuel pump inlet,also have great impacts on the common rail pressure control.

The proportional-integral-differential (PID) controller is one of the most popular solutions,as reported in[3].It is simple to implement but shows poor robustness and the parameters tuning is time-demanding [3]. Recent development in this field involves more sophisticated and precise control solutions. As an example, in [4], a single neuron adaptive PID controller for rail pressure is designed,where the neuron network training requires a large amount of data.In another approach,the quantitative feedback theory was applied[5],showing improved performance over the traditional PID controller.In[6],a time-varying internal model based controller was developed,to compensate for the rail pressure pulsations.The sliding mode controller,as developed in[7],was shown to achieve fast transient response, but was still struggling with the chattering issue. The triple step method was proposed by Hong Chen et.al in[8],combining the steady-state control,a feed-forward control concerning the variation of the tracking reference,and a non-linear error feedback.In our previous work as shown in[3],the active disturbance rejection control(ADRC)was applied to both gasoline and diesel engines. Similar work was also reported by Qifang Liu in[9].Results confirmed the superiority over the conventional PID controller. Meng Du et. al [10] proposed the variable parameter ADRC for the gasoline engine rail pressure control, as a competitive solution for the benchmark problem[11].

In this work, an extended state observer (ESO) [12]based model predictive control (MPC) solution for the rail pressure control is proposed for gasoline engines applications.Different from conventional MPC[13],the effects of the model discrepancy of the model used in MPC from the real plant are lumped as total disturbance and estimated by ESO. This allows the MPC controller to use a simplified model for reduced computational burden.This was shown to work well for the air system control of diesel engines as discussed in [14,15]. The control performance with the ESO-MPC solution will be compared with that achieved with the conventional PID controller,based on high fidelity model provided in the benchmark problem[11].The effects of the bandwidth of ESO on the control performance and the reliance on model accuracy will also be discussed.The proposed rail pressure controller is also applicable to Diesel engines,since the operating principles is similar.

2 System modeling

The common rail system for a gasoline engine is considered.The system specifications are listed in Table 1.The plant layout, as shown in Fig.1, includes the common rail, the injectors, and the high pressure pumping with a solenoid(pressure control valve,denoted as PCV)mounted.There is a pressure sensor mounted at the end of the common rail for feedback control.

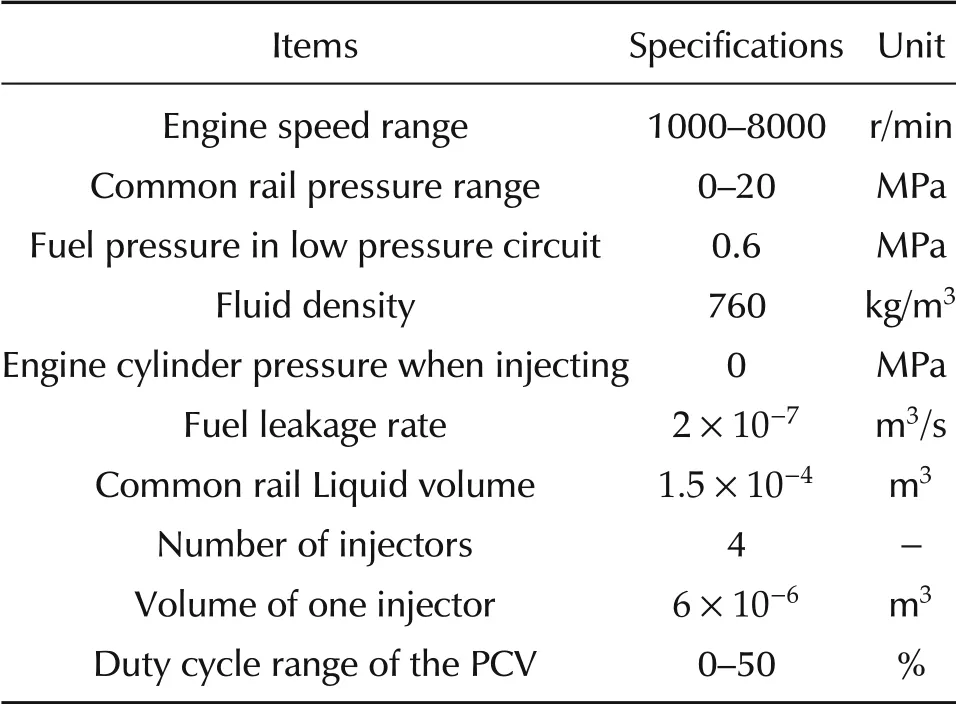
Table 1 The common rail system specifications[16].

The fuel is pumped from the fuel tank to the HP pump at an inlet pressure of 3-5 bar, driven mechanically by the engine crankshaft. The fuel flow rate into the HP pump is affected by the open/close timing and state(position) of the PCV. The duty cycle of pulse width modulation (PWM) signal is used to control the timing and position of the PCV.The amount of fuel flowing out of the common rail is influenced by the injecting duration of the injectors. The difference between the flow rates into and out of the common rail determines the pressure dynamic. Therefore, from a control point of view,the manipulative actuators is the PCV, which has to be controlled to maintain the common rail pressure at the desired value in the presence of disturbances,such as the variations in injection duration. Detailed modeling work was introduced in the paper[16]by Qifang Liu.For completeness,the model that includes the PCV,the high pressure fuel pumping, the common rail, and the injectors are represented by equations(1)and(2).

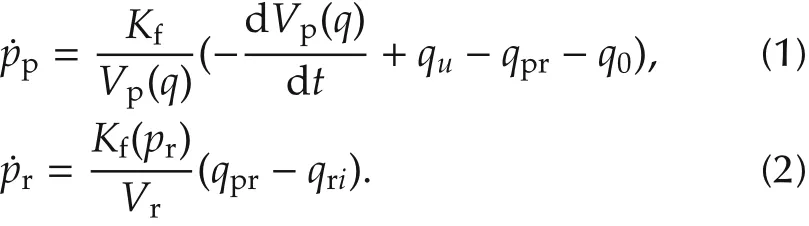
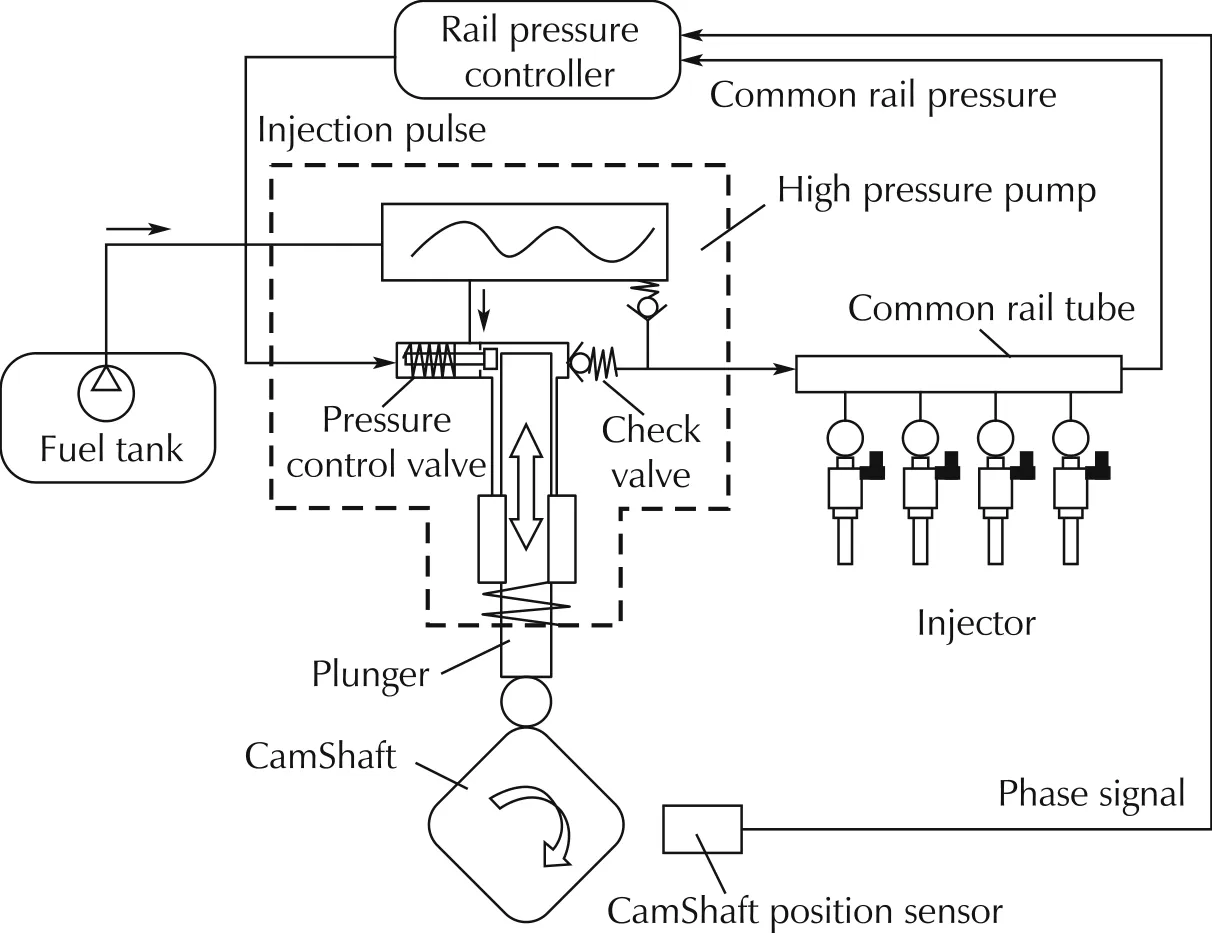
Fig.1 The schematic diagram of the high pressure common rail system[16].

In equation(1), ˙ppis the pressure of the chamber inside the high pressure pump, Kfis the bulk moduls of elasticity, quand qprare the inlet flow rate and outlet flow rate of the high pressure pump respectively,and q0is the fuel leakage caused by the clearance fit.

In equation(2),qriis the outlet flow rate of the common rail tube,that is,the total amount of fuel supplied to the four injectors in our plant. Vrand Kf(pr) are the volume and elastic modulus of the common rail tube respectively.

The sub-elements,Vp(θ),qu,qpr,and qriin equations(1)and(2)are explained as below:

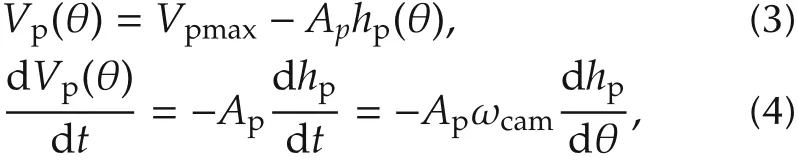
where Vpmaxis the maximum volume of high pressure pump chamber,hpis the plunger lift,which is a nonlinear function related to cam line,Apis the sectional area of plunger,θ and ωcamrefer to the angles and speeds of the cam respectively.

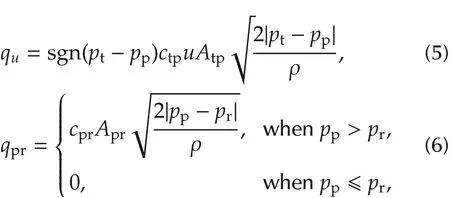
where ptis the pressure of the low pressure circuit,ctp,cprrefer to the flow coefficients at the inlet and outlet of the high-pressure pump respectively,Atp,Aprare cross section area of inlet and outlet of high pressure pump respectively,ρ is the density of the fuel,u is the duty cycle of the PWM signal,which is generated by the engine control unit(ECU).

For simplicity in control design, equation (6) is simplified as a linear equation,

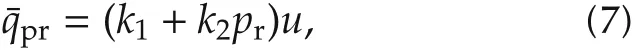
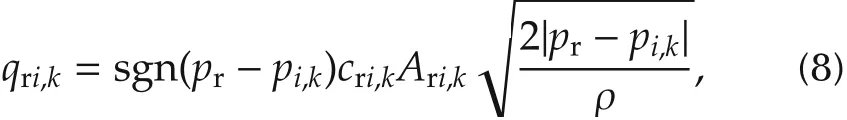
where Ari,kis the cross-sectional of the injector inlet port, cri,kis the liquid flow coefficient of the injector inlet port, pr-pi,krefers to the pressure difference between the common rail tube and the control chamber inside the injector.

The summation of qri,k(i = 1,2,...,4), i.e.,, are simplified by a linear function as in(9).

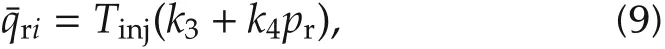
Substitute (8) and (9) into the common rail pressure dynamic(2),the following dynamic equation can be obtained:

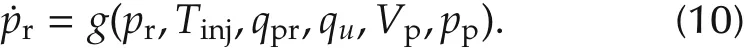
By approximating qribyin(8),and approximating qprbyin (9), the common rail pressure dynamic in(2)can be rewritten as

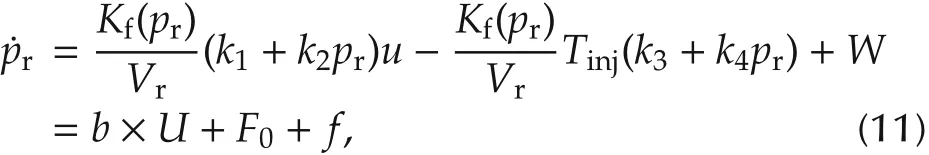
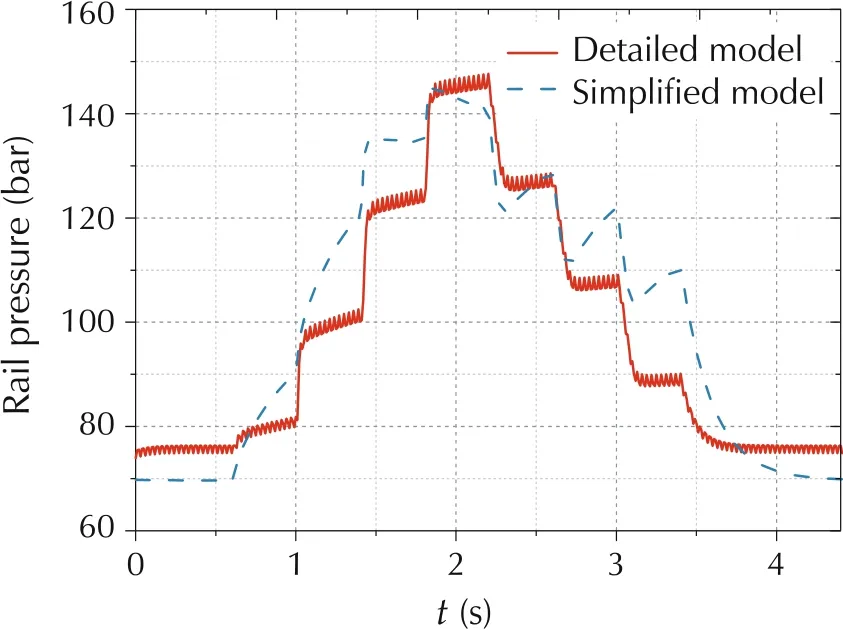
Fig.2 Validation of the simplified model.

3 Controller development

The control objectives of the CRHPS (common rail high pressure system)can be summarized as below.

1)Minimize the tracking error of the rail pressure.

2)Avoid control effort u saturation and minimize high frequency control switching ˙u.

3) Reject the unknown disturbances to maintain the desired rail pressure.

These objectives are expressed mathematically as

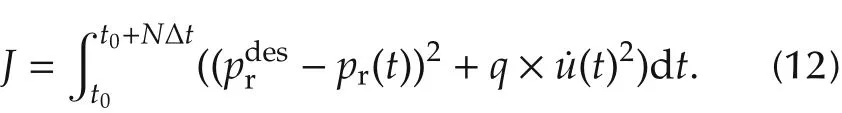
In the cost function in (12), t ∈[t0,t0+NΔt], Δt is the sampling period,and NΔt is the horizon over which the optimal solution is sought, q is weighting factor matrix to be tuned, ˙u is the derivative of the control input u.The following state and control constraints can also be enforced:

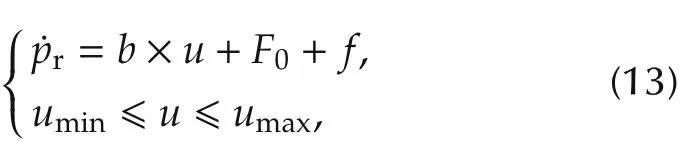
The subscripts min and max denote the minimum and maximum values respectively for the box constraints.The schematic of the ESO-MPC control architecture is shown in Fig.3. The sampling period of the ESO-MPC controller is 1 ms,and the prediction horizon of MPC is 10 steps.

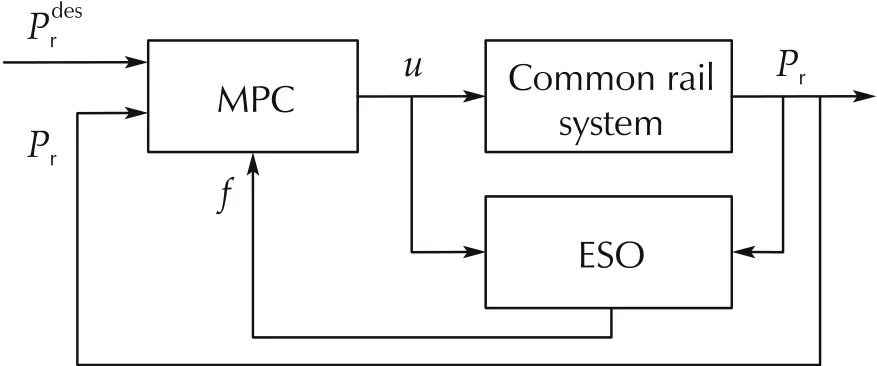
Fig.3 Control structure of the ESO-MPC controller.

3.1 Model predictive controller

The corresponding duty cycle of the PCV driven signal,u,is determined from the solution of a MPC problem with the cost function similar to(12),as defined in(14).In equation(14),the box constraints on the control input is retained by introducing φ1(u,t)and φ2(u,t).

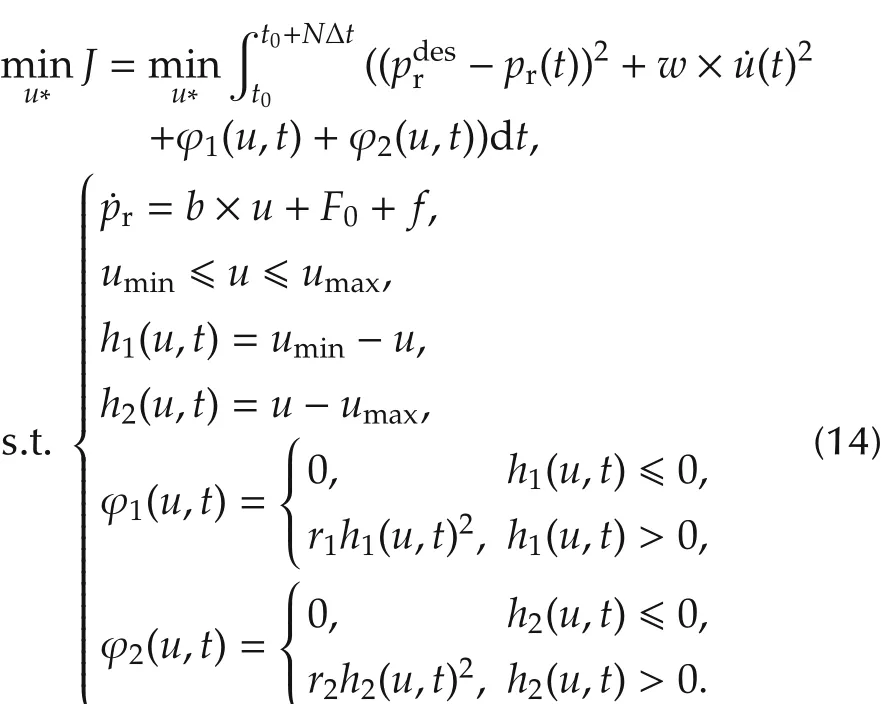
In equation (14), φ1(u,t) and φ2(u,t) are introduced to handle the box constraint,using the exterior penalty method [17], w is the penalty for the derivative of u.Note that in the MPC problem,F0and f are assumed to be constant over the prediction horizon.This MPC problem is then solved using the nonlinear MPC algorithm from [17]. Specifically, the Newton/generalized minimum residual [18] (N/GMRES) algorithm is adopted.This algorithm is based on the continuation method combined with a fast algorithm for linear equations instead of the Ricatti differential equation and provides a fast and stable numerical solution.

3.2 Extended state observer

Note that in(14),the total disturbance, f,is unknown and not measureable.In order to estimate f in real-time,the ESO method[12]is used by augmenting the original model in (11) with an additional state f, and rewritten(11)in the extended state form:Equation(15)can be written in state space form as,are the states,y=x1is the measured output,d= ˙ˆf is unknown.

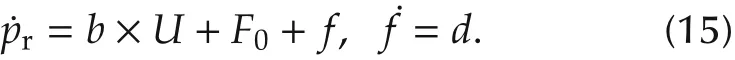
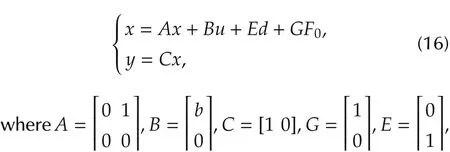
The ESO for the state space representation in equation (16) is designed as in (17), following the method shown in[19].

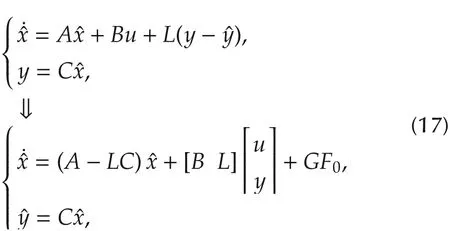
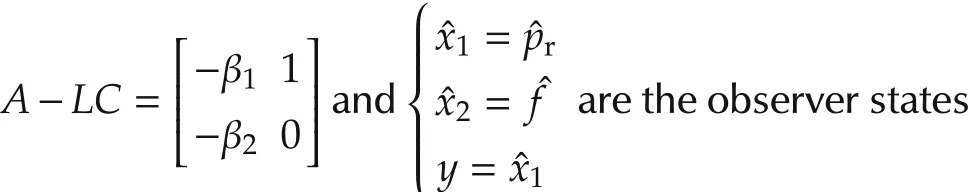
and measurement estimates,respectively.

Tuning of the ESO gain matrix is addressed using the bandwidth parameterized method proposed by Gao [19]. This is briefly introduced here for completeness.The characteristic polynomial for the ESO system,equation (17), is s2+β1s+β2= 0. Since β1and β2are design variables,these can be selected to make the ESO state space Hurwitz stable.If we recognize that the characteristic polynomial may be represented as a damped second order system,that is,s2+β1s+β2≡s2+2ξωos+ω2owith ξ and ωobeing the damping coefficient and the natural frequency(bandwidth),respectively,of the ESO system,the ESO observer gains,β1and β2are then easily determined through the selection of a system bandwidth and damping as follows:

It is possible to make both ξ and ωotime varying and allow a dynamic selection for ωo.In this paper,for simplicity,the damping ratio ξ is fixed at 1.Hence,the eigenvalues for A-LC in equation(17)are determined by the system bandwidth ωo.After convergence of ESO,ˆx1→x1→pr, ˆx2→x2→f,and then f can be used in the MPC controller.

4 Controller validation

In this section, simulation results from the implementation of the proposed ESO-MPC controller were shown, which were compared with results from the conventional PID controller. The simulation was conducted on the simulation model proposed by Qifang Liu in[16].The model was derived for the fuel rail injection system based on hydrodynamics and the bulk modulus of elasticity and simplified reasonably for the controller design[16].The model was implemented in Matlab/Simulink. Performance metrics, such as the settling time,overshoot,maximum deviation from the target rail pressure,were assessed.The PID controller parameters and the ESO-MPC controller parameters are shown in Table 2.

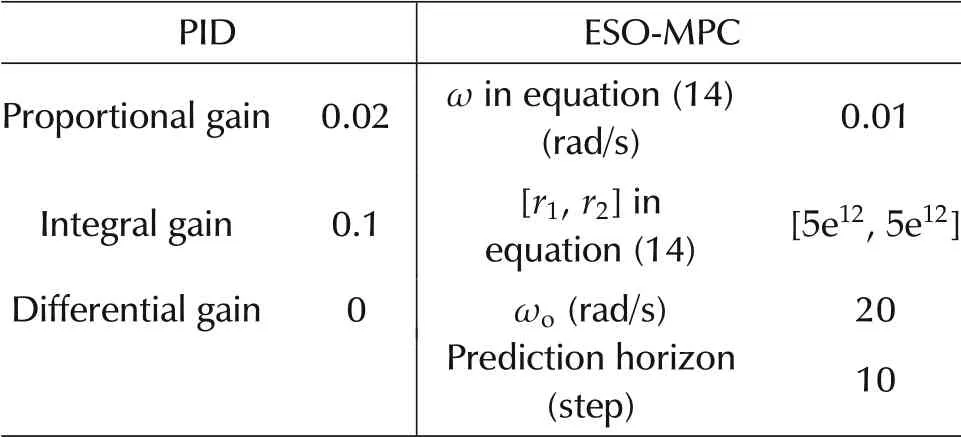
Table 2 Controller parameters.

4.1 Rail pressure step response test

To evaluate the transient response of the rail pressure controller, a rail pressure step from 110 bar to 130 bar was carried out at 3000 r/min engine speed and 2.2 ms single pulse injection. As can be seen, for rail pressure tracking,the first plot in Fig.4,the ESO-MPC controller improves the transient response by 10%in terms of setting time, and 2.63% in terms of integrated absolute tracking error (IAE). The detailed performance metrics were tabulated in Table 3. An interesting observation is that at quasi-steady state condition(1.65 s to 1.75 s),the ESO-MPC controller produces 25%lower variations of duty cycle (13% to 15%), relative to that with PID controller(5%to 13%).Additionally,ESO-MPC also reduces the IAE of the rail pressure by 4.87% compared to that with PID control. This is beneficial to improve the durability of the fuel system and reduce the energy cost. Another observation is that the absolute value of the duty cycle using ESO-MPC is higher than PID controller.The primary reason is that with the baseline PID controller, it takes greater than 0.5 s for the rail pressure to settle down, which is in line with the findings in the reference paper by Meng Du et al. [10]. In contrast, the ESO-MPC controller converges much faster than PID. Simulation results show that with time going on(＞2s),the mean values of the duty cycles from PID and ESO-MPC will converge, even though the duty cycle variations are different. This is applicable to all the results in this paper.

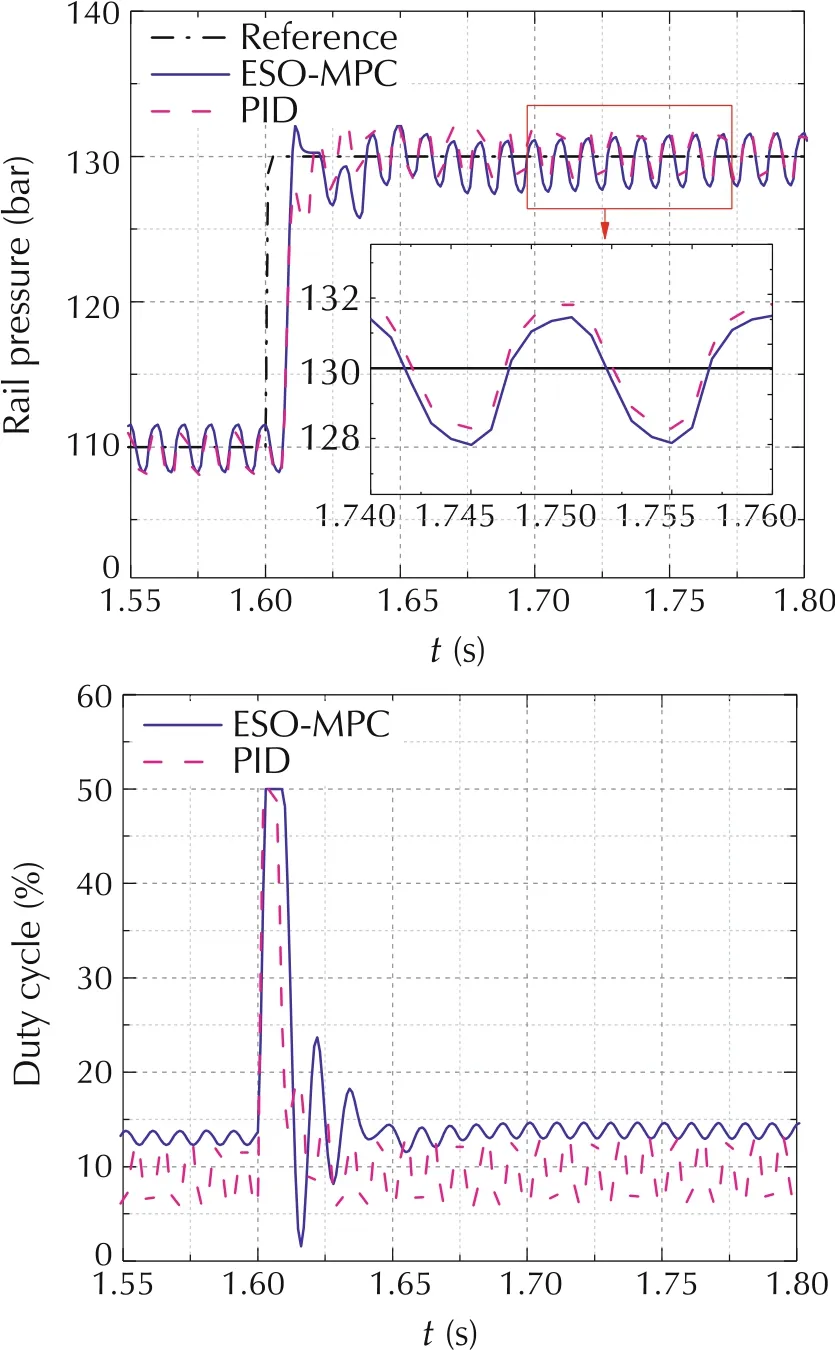
Fig. 4 Performance comparison in target rail pressure step from 110 bar to 130 bar at 3000 r/min engine speed and 2.2 ms injection pulse.

Similarly, in the step down test of the rail pressure from 130 bar to 110 bar, the ESO-MPC controller improves the transient response by 8.39%in terms of IAE during the time interval of 2.8 s to 3.0 s,and 27.46%in terms of overshoot as indicated in Table 4. The benefit in the reduced variation of duty cycle at quasi-steady state is also observed. Fig.5 Performance comparison in target rail pressure step from 130 bar to 110 bar at 3000 r/min engine speed and 2.2 ms injection pulse.

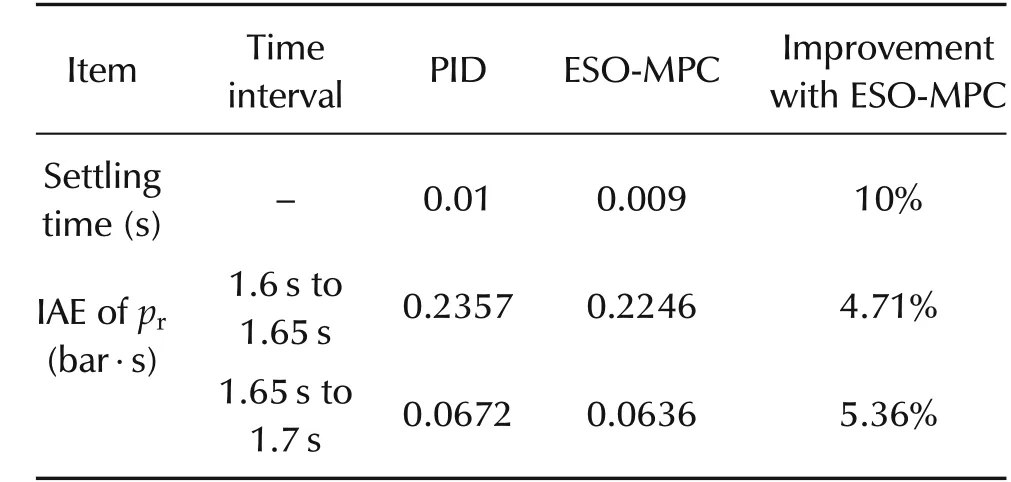
Table 3 Performance comparison between PID and ESO-MPC in rail pressure step-up.

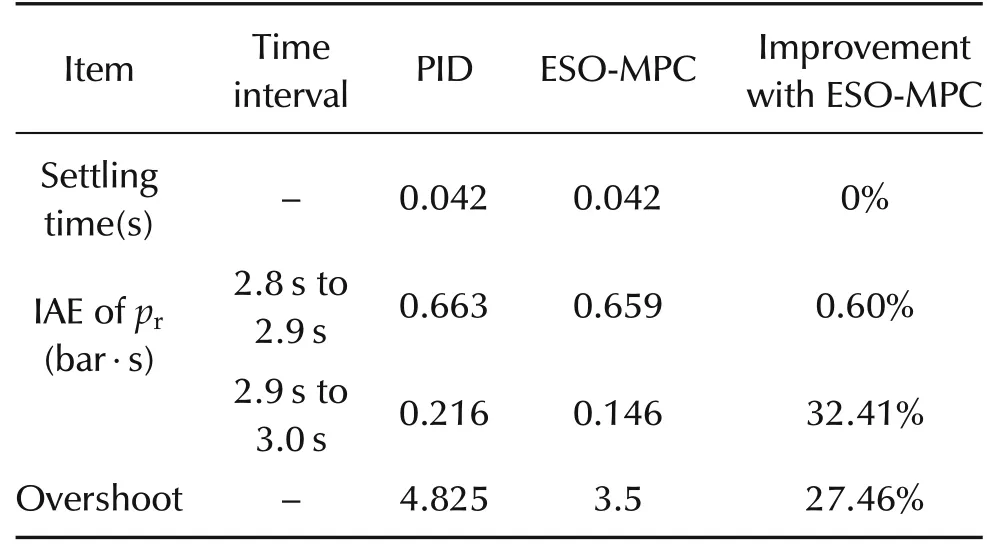
Table 4 Performance comparison between PID and ESO-MPC in rail pressure step-down.

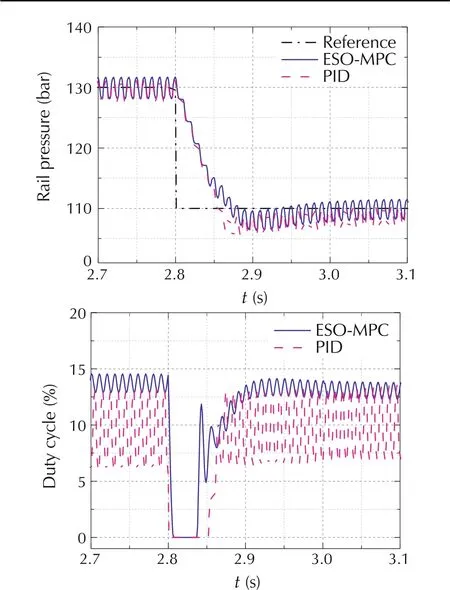
Fig. 5 Performance comparison in target rail pressure step from 130 bar to 110 bar at 3000 r/min engine speed and 2.2 ms injection pulse.

4.2 Disturbance rejection capability to fuel rate step

The change of the injection rate is one of the most significant disturbances to rail pressure control.In order to maintain stable and accurate rail pressure control,the controller needs sufficient disturbance rejection capability.The performances with ESO-MPC and PID controller were assessed at 3000 r/min engine speed with fuel rate stepping from 4 ms to 2.2 ms, as shown in Fig.6. The IAE from 2.4 s to 2.6 s with the ESO-MPC controller is 0.236 bar·s,which is 12.09%shorter than that achieved with the PID controller. The recovering time, the time elapsed from 2.4 s to the time at which the rail pressure deviation from the target value has entered and remained within the error band of ±2.5 bar, also confirmed the superiority using the ESO-MPC solution(50%shorter than that with the PID controller).The difference between the two average values of the duty cycle is due to the fact that the duty cycle with the PID has not converged to the steady-state value yet.

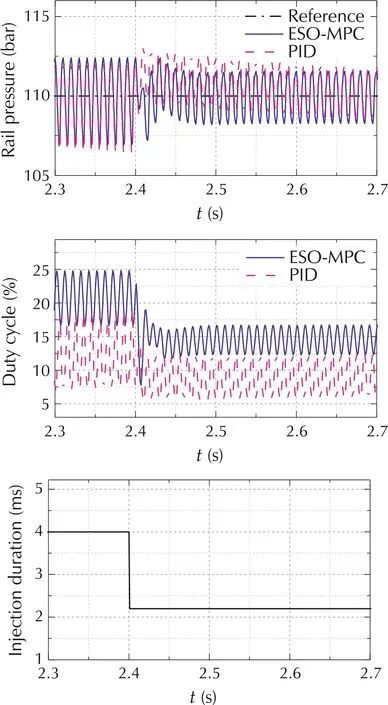
Fig. 6 Disturbance rejection performance comparison with fuel rate stepping from 4ms to 2.2ms in at 3000 r/min engine speed.

4.3 Robustness over wide operating range

In this section, the robustness of the ESO-MPC controller was compared with the conventional PID controller at different engine speeds and fuel rates,as shown in Fig.7.The performance metrics,such as settling time and IAE of the tracking error are tabulated in Table 5.

As is seen, the PID controller is not able to maintain the control performance over the listed operating range.Specifically, the response is quite sluggish at low rail pressure condition,while overshoot is seen at high pressure conditions.This drives the need for gain scheduling.In contrast, using the ESO-MPC controller, satisfactory performance is maintained over the investigated operating range.The primary reason for this comes from the compensation effect by using ESO, as indicated in the third plot in Fig.7.

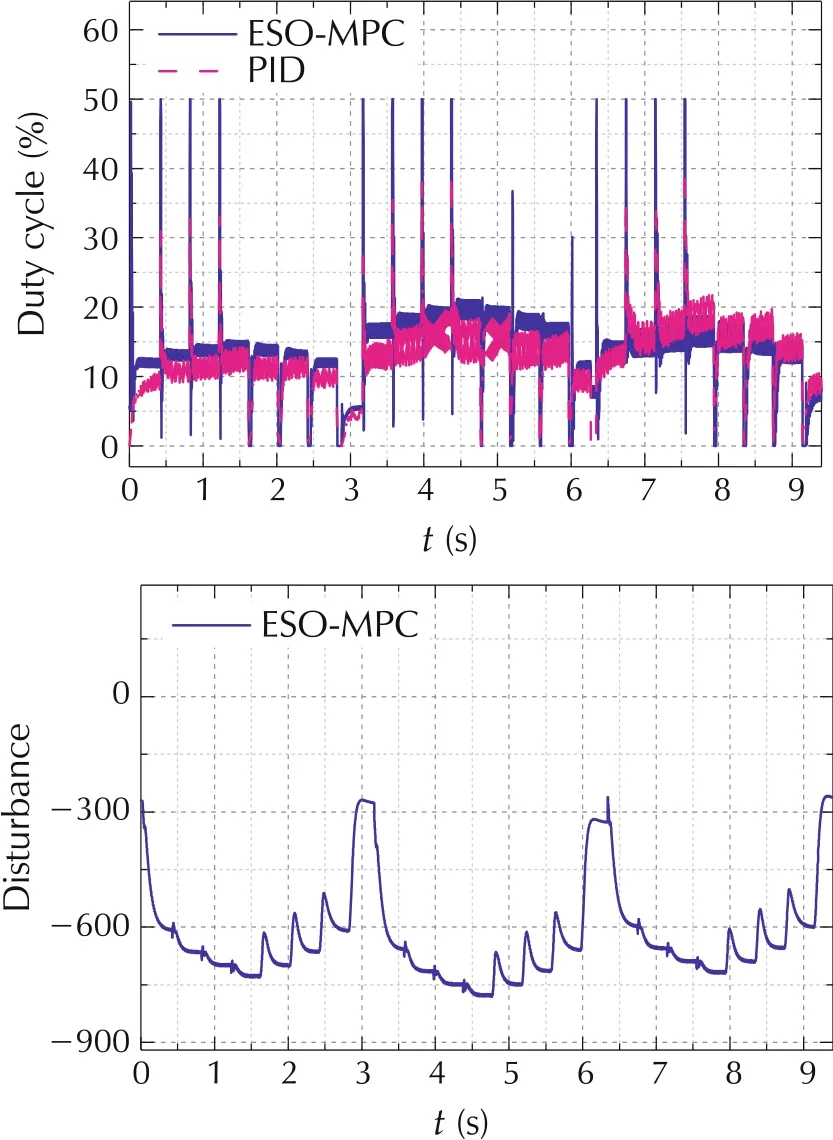
Fig. 7 Disturbance rejection performance comparison with fuel rate stepping from 4 ms to 2.2 ms and engine speed stepping from 3000 r/min to 2000 r/min.

Another observation is that the computation time of ESO-MPC controller is higher than that of PID controller,which are 0.72 ms and 0.04 ms,respectively.

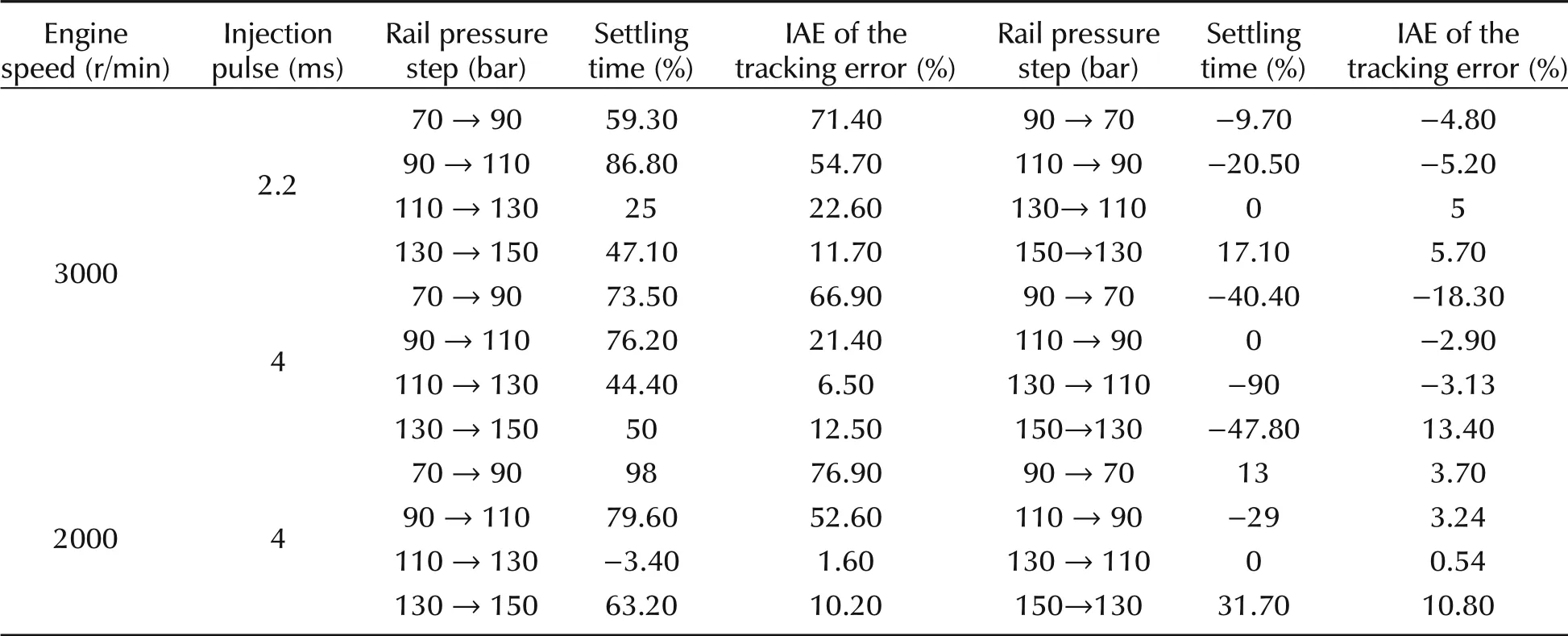
Table 5 Improvement(%)from using ESO-MPC relative to the PID controller.

4.4 The impact of ESO bandwidth on control performance and complexity

4.4.1 The trade-off between disturbance rejection and noise sensitivity

In the proposed ESO-MPC controller,the ESO was used to observe the uncertainties in the MPC controller.To evaluate the impact of ESO on the control performance,a fuel rate step from 2.2ms to 4ms at 3000 r/min engine speed was carried out from 4.8 s. Different ωowere selected,namely,20 rad/s,40 rad/s and 100 rad/s.

As can be seen, for rail pressure tracking in the first plot in Fig.8 with ωo=20 rad/s,it converges much more slowly relative to the ωo= 40 rad/s and ωo= 100 rad/s cases, caused by the slow convergence of f, as shown in the second plot in Fig.8.Because of the slow convergence of f,there is large difference in f between three cases as shown in the time period from 4.9 s to 5.25 s in Fig.8. The difference will vanish as the elapsed time is greater than 5 s. However, for ωo= 100 rad/s case, the variation of the duty cycle is much larger relative to the other two cases. The performance metrics are listed in Table 6.Results indicate that there is trade-off between the estimation accuracy and the noise sensitivity.

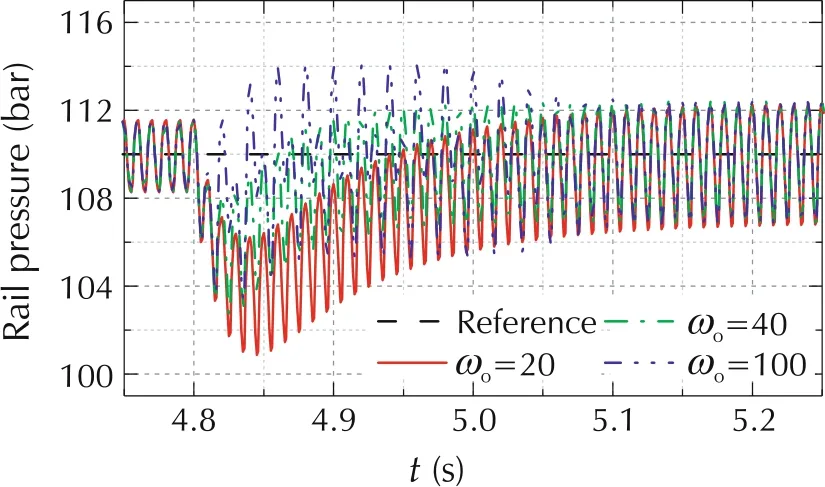
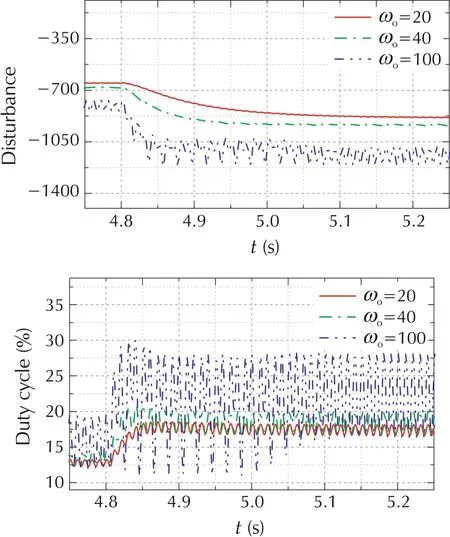
Fig. 8 The impacts of ESO bandwidth on the disturbance rejection capability at 3000 r/min engine speed in the face of fuel rate step from 2.2 ms to 4 ms from 4.8 s.

Table 6 Impacts of ESO bandwidth(ωo)on the disturbance rejection performance.

4.4.2 Appropriately selected ESO bandwidth allows reducing model complexity

The computational burden and the memory occupation are concerns for the conventional MPC controller.In the proposed solution,the utilization of ESO offers the opportunity to reduce the model complexity by lumping the effects of model inaccuracy as total disturbance to be estimated by ESO.In order to verify this,the controller performance, obtained from a simplified controller by assuming F0= 0 in (11), is compared with the original controller developed in Section 4(the complete expression of F0is used).

By observing the results shown in Fig.9 and the performance metrics listed in Table 7,the following observations become clear.

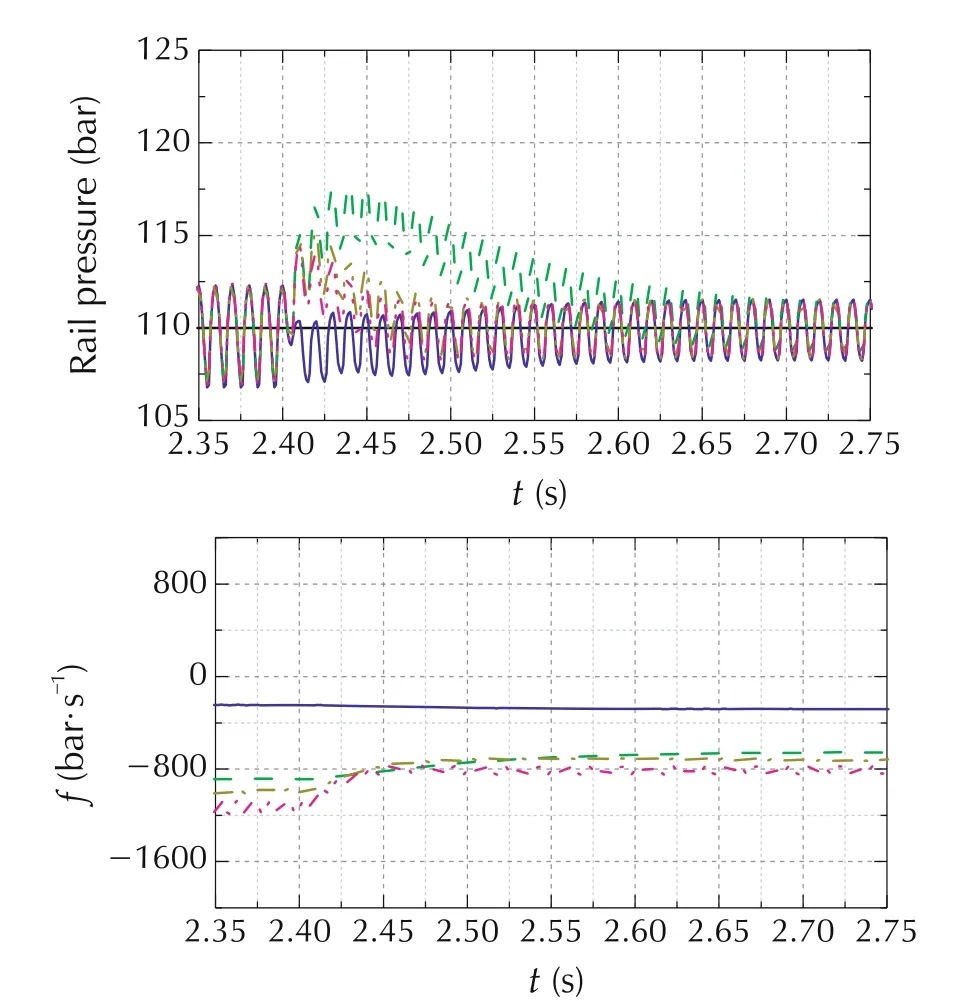
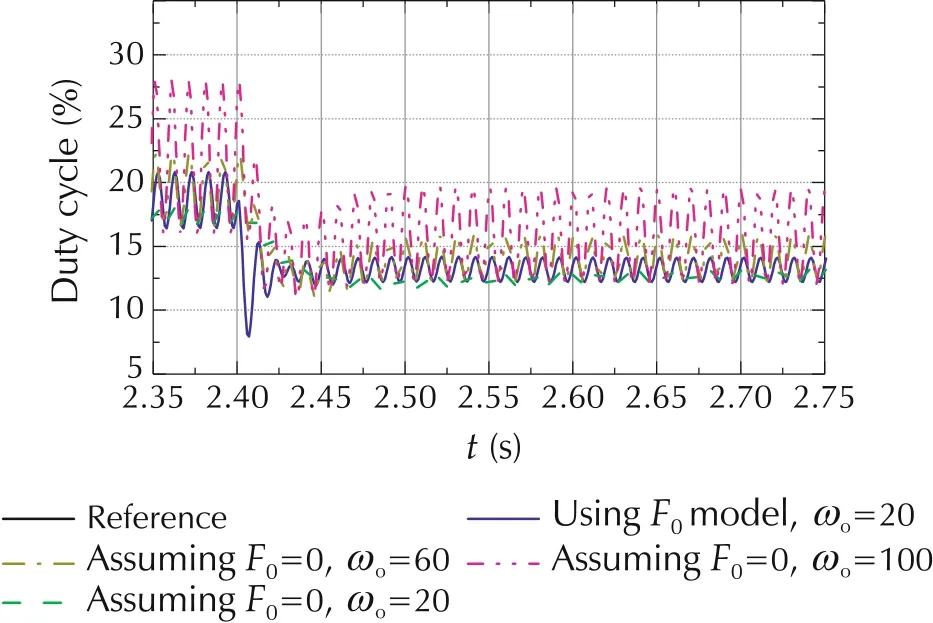
Fig.9 Performance comparison between ESO with F0 model and ESO with F0 =0(using different ESO bandwidths).

1)By comparing case 1 and case 2,it is clear that detailed model provides improved disturbance rejection capability,since there is reduced amount of total disturbance to be observed.

2)By comparing case 1 and cases 3,it is seen that even with reduced model complexity,i.e.,assuming F0=0,a satisfactory control performance can still be achieved by appropriately increasing the ESO bandwidth.This is primarily because of the disturbance observation capability of ESO.

3) Over-increasing the ESO bandwidth leads to control process oscillation.

4) With F0in (11) simplified as 0, the disturbance,f,deviates larger from zero,relative to the original controller.This is simply because of the effects of simplifying F0as 0 is lumped into f.

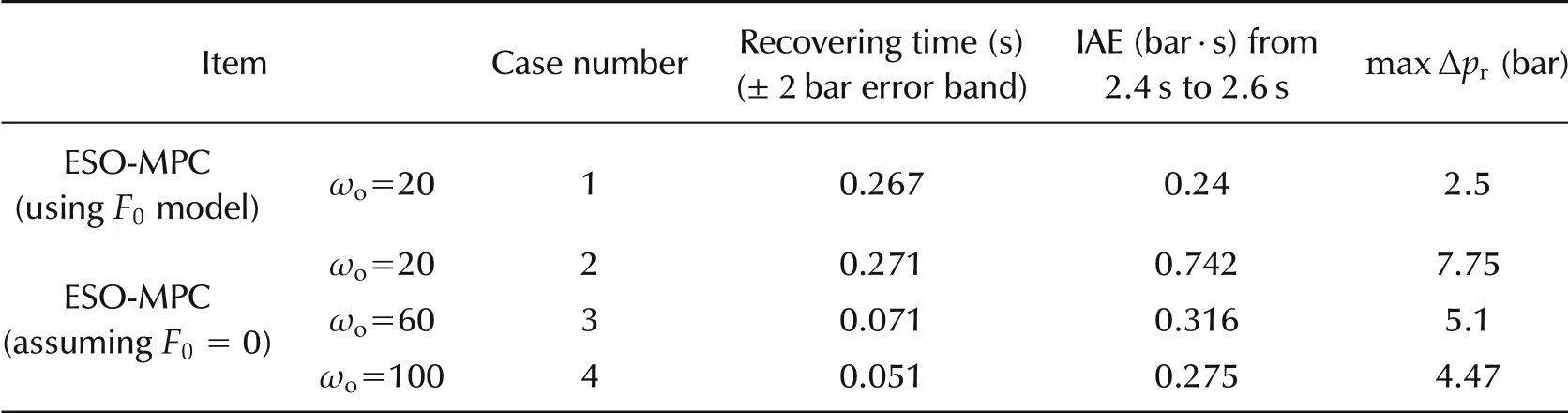
Table 7 Appropriately selected ESO bandwidth ωo allows reducing model complexity.

5 Conclusions

In this paper, an ESO-MPC controller was proposed,for the rail pressure control of gasoline engines.

The main conclusions were listed below.

1) By simplifying the rail pressure dynamic as a simple first order system to be used in MPC while treating the model discrepancy from the real plant as total disturbance to be estimated by ESO,an ESO assisted MPC solution was proposed.The Newton/GMRES algorithm was used to solve the MPC problem.

2) The proposed controller was evaluated on a high fidelity model provided in a benchmark problem. In comparison with the conventional PID controller, the ESO-MPC solution improved the rail pressure transient response by 5%in terms of the integrated absolute tracking error,and enhanced the disturbance rejection ability,in the face of fuel rate step,by 12%in terms of recovery time.

3)Additional simulation results showed that the ESOMPC solution is able to maintain the control performance over a much wider operating ranging,relative to the PID controller. The maximum improvement in settling time is up to 77%. This comes from the benefits from using the ESO.

4) The effects of the ESO bandwidth were analyzed.Results confirmed that the complexity of the model used in MPC can be reduced by appropriately increasing the bandwidth of the ESO, with the upper bound of ESO bandwidth limited by the noise sensitivity. Therefore,the ESO-MPC combination offers a simpler and more practical solution relative to the conventional MPC.

6 Nomenclature

1)Variables

A:Area(m2).

c:Flow coefficient.

k:Parameters for identification in the simplified model.

K:The bulk moduls of elasticity.

p:Pressure.

q:Flow rate(kg/s).

u:The control input:duty cycle(%).

V:Volume m3.

ρ:Density(kg/m3).

θ:Camshaft angle.

h:Lift(m).

2)Subscript

ri:From the rail into the injector.

pr:From the pump into the common rail tube.

p:Pump.

r:The common rail tube.

cam:Camshaft.

max:Maximum value.

f:Fuel.

tp:The inlet of the high pressure fuel pump.

inj:Injection.

des:Desired.