Revisiting the benchmark problem of starting control of combustion engines

Jiangyan ZHANG , Zhenhui XU , Jinwu GAO

1.State Key Laboratory of Automotive Simulation and Control,Changchun Jilin 130025,China;

2.Department of Control Science and Engineering,Jilin University,Changchun Jilin 130025,China;

3.College of Mechanical and Electronic Engineering,Dalian Minzu University,Dalian Liaoning 116600,China;

4.Department of Engineering and Applied Sciences,Sophia University,Tokyo,102-8554,Japan

Abstract Starting of combustion engines is a typical transient operating mode that has significant influence to the engine performance.Due to the distinct variations in the pathes of air intake and fuel injection,the model of the engine system contains considerable uncertain parameters.To search effective control schemes that guarantee desired performance,engine starting control is proposed as a benchmark challenge problem.As a challenging result,a model-based control scheme is developed perviously.In this work,the benchmark problem is revisited and a modification for the fuel injection path control of the previous work is proposed by integrating a time sequence regressive based parameter tuning strategy.Validation by the benchmark problem simulator shows that although the new strategy has simple structure, similar control performance is obtained. Especially, the new strategy has potential extensibility with learning based methods to further improve the performance of the benchmark problem on engine starting control.

Keywords: Combustion engine,starting control,transient performance,benchmark challenging

1 Introduction

The SICE benchmark problem on starting control of combustion engine is proposed by the research committee on advanced engine powertrain control theory of Society of Instrument and Control Engineers (SICE)of Japan [1]. The challenging problem is motivated by automotive industry, and is formulated by industrialacademic collaboration. During the last ten years, several challenging results have been reported from both sides of academic and industrial community as reported in the papers[2-7].Meanwhile,the technology of quick starting control which is targeted by the benchmark problem has been widely applied to the production engines with the conception such as idling stop, fuel cutting,especially mode switching in hybrid electric powertrain[8,9]where the combustion engine is stopped and restarted frequently. However, it is still an open challenging issue to starting a combustion engine with high performance.

The most challenge in starting of gasoline engine is the controls for the air path and fuel path,since the dynamics of the air intake path and the fuel injection path are dramatically changed during the first a few combustion cycles.For example,the intake manifold pressure is normally high during the cranking period before getting the first firing in cylinder. In this case, the air charge is much over than the required volume, and as a result,it will lead to over torque generation that drives the crank to higher overshoot. Moreover, the wall-wetting phenomenon causes cylinder-to-cylinder and cycle-tocycle variation in the fuel mass injected to individual cylinders. Therefore, it is difficult to handle the fuel injection mass during the first a few cycles. In the result in[7]presented by the first author of this paper,an openloop observer-based air charge mass estimation method is proposed and with the estimation, the fuel injection is decided individually where the fuel injection mass of each cylinder is generated by an inverse-dynamicsbased prediction.It should be noted that this approach is in principle a model-depended approach. However,obtaining a model of air intake path with higher accuracy is a difficult task,and estimation provided by open-loop observer depends on the model accuracy.

In this paper,we revisit this challenging problem.The aim of this work is to simplify the fuel path control design of the proposed approach in [7] by removing the open-loop observer. Instead of the observer-based control law, an autoregressive model with feedforward of air mass flow is proposed. Top dead center (TDC)-based and cycle-based multi-sampling rates are used for the time sequence regressive model. It allows to use learning algorithm for the regressive model parameters.Combining with the control loops for the ignition and the throttle opening, the modified control scheme is validated with the simulator provided by the SICE benchmark problem[10,11].

2 Brief review of the benchmark problem

The benchmark problem on starting control considers a V-type four-stroke spark ignition (SI) engine with six cylinders as sketched in Fig.1 where only one cylinder is plotted for simplicity.

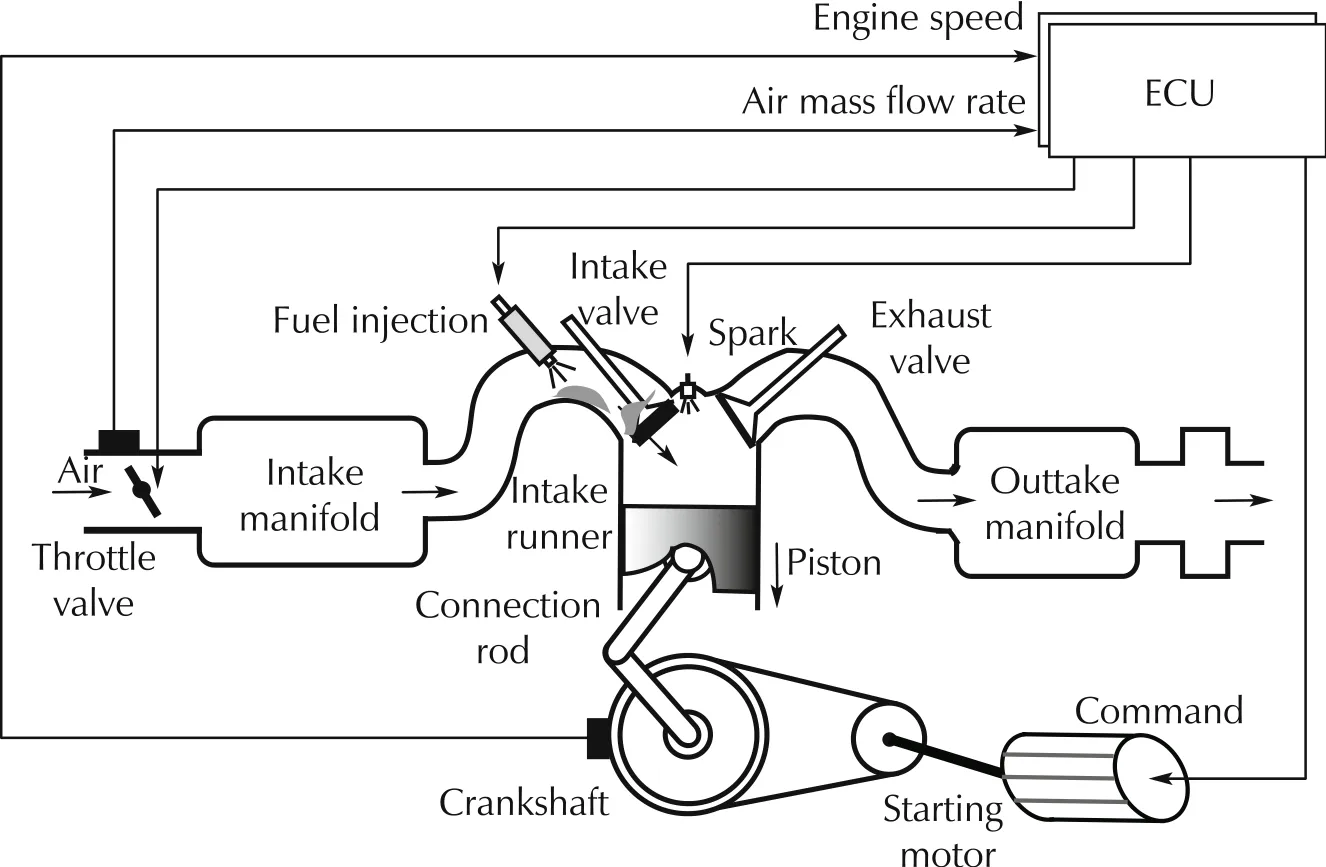
Fig.1 Schematic of engine system.

When the engine starts to provide driving torque for a vehicle, it relies on an initial rotational speed of the crankshaft performed by the equipped starting motor.Then, according to the commands from the electronic control unit(ECU)of the engine,the starting motor is cut off and each cylinder starts to generate driving torque serially acted at the crankshaft. The rotational speed of the crankshaft is the so-called engine speed which is concerned at this work.The main purpose of the engine starting control is to let the engine speed be quickly and smoothly stable at a desired value.The performance of the starting speed is determined by the proper control of the driving torque which is generated by the combustion of the air-fuel mixture in each cylinder.

During the intake stroke,the air intake into the cylinders is through the air path that consists of the throttle valve, the intake manifold, intake runner and the intake valve. For fuel injection, the engine system uses port injection, hence the fuel path of each cylinder possesses the wall-wetting phenomenon.Then,in each cylinder, the air-fuel mixture is ignited by the spark at the MBT(minimum spark advance(SA)for best torque)of the compression stroke. The generated energy by combustion is transferred to be the driving torque at the crankshaft due to the movement of the piston during the power stroke.Finally,the exhaust stroke follows and forms the emission of the vehicle.Moreover,for the engine with six cylinders,one cycle is completed in 720°crank angle θ,and the TDC timing interval of each cylinder is 120°.In view of the above facts,the actuators for the engine starting control include the throttle opening uth,the individual fuel injection ufiof each cylinder and the spark timing which is usually called as SA usiof each cylinder. That is, there are 13 control input variables,and the engine speed w is the output as shown in Fig.2.In addition, the air mass flow rate ˙mipassing through the throttle valve and the θ are measurable for control law development.

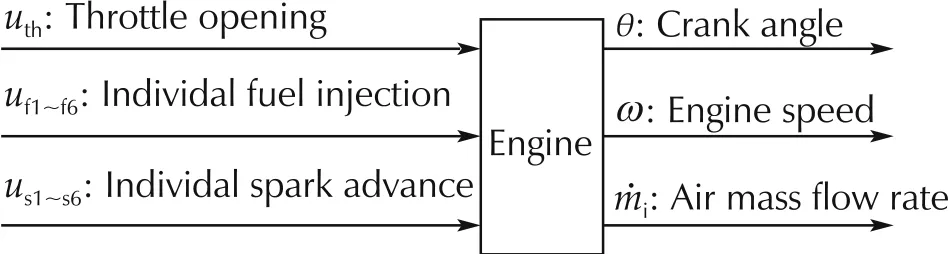
Fig.2 System inputs and outputs.

The constraint conditions for starting the engine in the benchmark problem and the design specifications for the starting engine speed are as shown in Table 1.

For the above formulated starting control problem,the challenging points lie in the proper management of the in-cylinder A/F during the first a few cycles for successful ignition, since the intake manifold has a higher pressure than the value at steady state, and the wallwetting phenomenon of each cylinder has distinct variance after the first combustion event. Moreover, to get the desired starting speed performance,the torque generation management by the coordination control of the 13 actuators is significant.

Evaluation of the proposed control scheme should use the provided simulator by the SICE benchmark problem.The simulator is constructed in Matlab/Simulink and is available from the attached CD ROM of the book[10].

Table 1 Problem formulation.

Finally, in the previous work [7], a control scheme that includes a fuel injection control block and control blocks for the throttle opening and SA, respectively, is proposed for successful combustion and starting speed regulation,shown in Fig.3.Note that the fuel path control is constructed with an open-loop observer and the inverse dynamics. In this work, the fuel path control block is redesigned by replacing the observer with a learning-based control law.

3 Modif ied approach

In this section,a new fuel control law is designed and combined with the control laws of the SA and throttle opening, to solve the benchmark problem. In particular, the redesigning of the fuel injection control law includes two steps: first, propose a control law based on autoregressive model with feedforward of air mass;then identify the model parameters in the controller by auto-tuning algorithm.

3.1 Fuel path control law

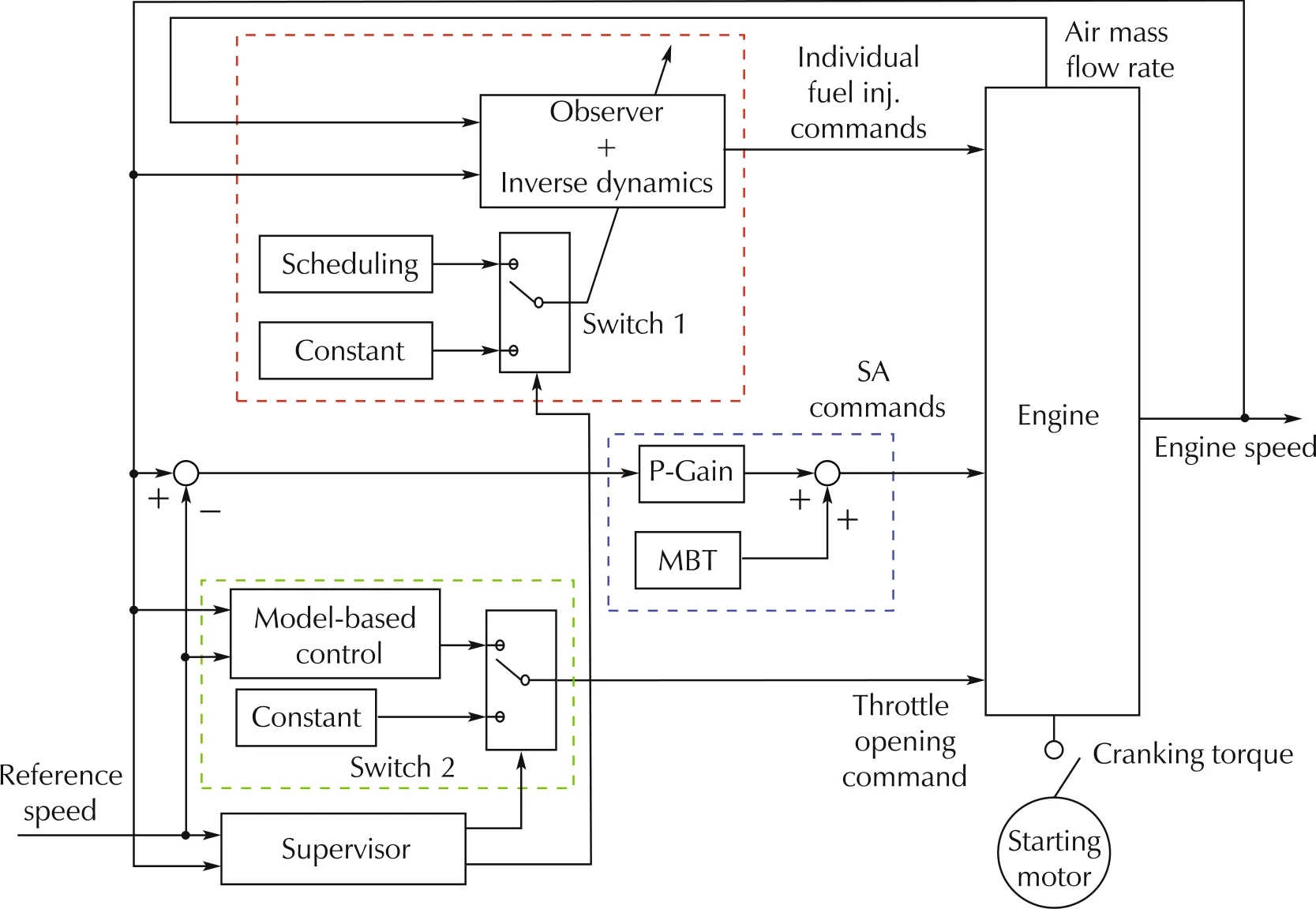
Fig.3 Block diagram of previous proposed control scheme in[7].

To decide the fuel injection mass for each cylinder,especially, during the transient response period at the starting operation,the air charge estimation of individual cylinder is a bottleneck due to the dramatic variation of the air state in the intake manifold and the wall-wetting phenomenon.Due to the constraint on A/F of the benchmark problem, the manifold state and wall-wetting for the fuel path control design are the main factors for determining the air and the fuel mass in individual cylinders.In the following,an autoregressive model of the air path is constructed first to realize the air charge estimation. With the air charge estimation, the fuel injection control law for each cylinder can be designed based on the fuel path wall-wetting dynamical model.

It is known that the behavior of the air path can be characterised by the following equations:

where pmdenotes the intake manifold pressure, c1and c2are composed coefficients with time-varying physical parameters, and ˙modenotes the air mass flow rate leaving the manifold into the cylinders. The fuel path is modeled as the well-known wall-wetting model as follows:

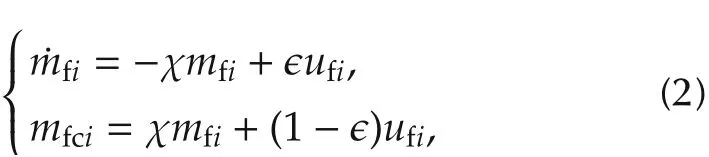
where mfiand mfcirepresent the fuel mass entering the intake port per induction stroke and the fuel mass injected into each cylinder,respectively,and ϵ and χ represent the fraction of fuel deposited on the inlet port and the inlet port time constant,respectively.

Since the individual fuel injections should be decided per 120°at each TDC timing, the air-path model is discretized with TDC-based sampling period with ˆtdc(l)=2π/(3ω(l))where l(=1,2,...)denotes the TDCbased sampling sequence (Note that l = 1 means the TDC timing of the cylinder that is first ignited).Then the model(1)is approximated by the forward differential as follows:

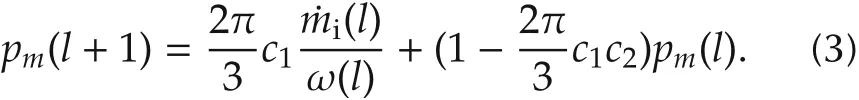
Furthermore,since the exact air charge for each cylinder can only be obtained after the whole intake stroke,while the fuel injection should be decided at the corresponding TDC timing,an estimation for the air charge of each cylinder is constructed by

where ˆmcylrepresents the air charge into each cylinder.Then, taking the relation (1b) and the equation (3) into account obtains the time serial model of the air charge estimation as follows:

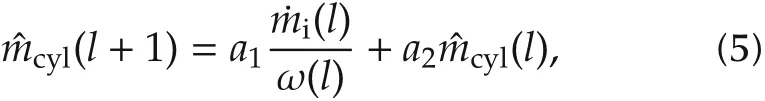
where a1=(2π/3)2c1·c2and a2=1-c1c22π/3.It should be noted that this regressive algorithm is deduced based on the intake manifold model(1),while no more parameters of the model (1) and pressure measurement are needed, since parameter of auto-regressive term and the external control term, a1and a2, might be directly tuned combining with the following fuel injection mass command.

With the air charge estimation(5),for the i th cylinder,the fuel injection during a cycle can be calculated as

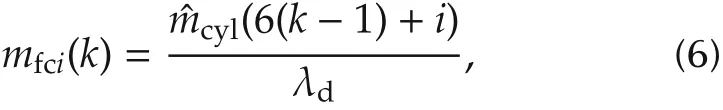
where λdrepresents the desired A/F and k denotes the cycle-based sampling sequence.For the engine with six cylinders,it can be deduced that the relation between k and l is k = f ix((l-1)/6)+1,where“f ix”is the Matlab function that rounds the element l-1 to the nearest integer towards zero.Then,in order to decide the individual fuel injection command for each cylinder,the fuel path model(2)is discretized with cycle-based sampling rate as follows:

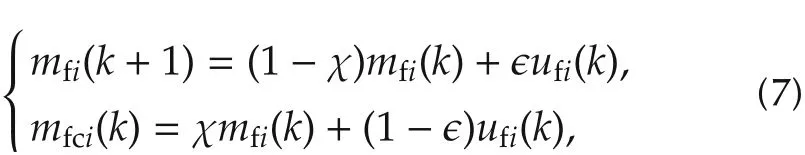
where i = 1,...,6.Finally,the fuel control law for individual fuel injection command can be obtained from the inverse dynamics of the model(7),

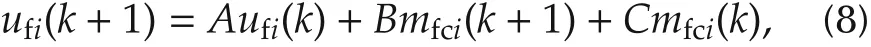
where

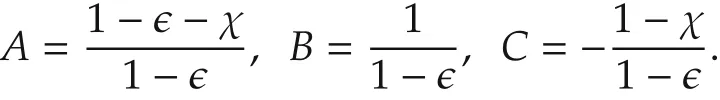
The above proposed control scheme for fuel injection is summarized as Fig.4.

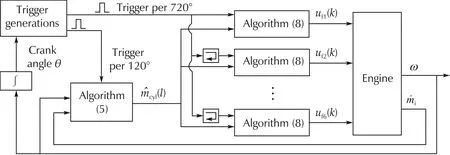
Fig.4 Structure of the fuel path control system.

3.2 Parameter-tuning algorithm

As a result, the fuel injection mass is decided by the algorithms(5)and(8)with two sampling rates.To guarantee successful firing and reject larger overshoot of starting speed response, the fuel injection mass at the first cycle is directly tuned with the coefficients of the algorithms(5)and(8).The evaluating index for the tuning is the overshoot and the regulating time.

For tuning the fuel injection mass of the first cycle,the only index is getting firing successful. Due to the initial position of the crank angle is uncertain, it is not possible to calculate exactly the fuel injection mass for the cylinder which gets the first firing and it is unknown which cylinder gets the first firing. Monitoring the first firing and followed by a few firing events in the other cylinders will lead to the decision of the fuel injection mass for the first cycle.Then,during a starting process,online tuning the parameters of algorithm(5)and(8)can be focused on stable combustion in the cylinders and rejection undesired over torque generation as possible.

It should be noted that tuning all parameters is not easy by online during the stating process,however,primary tuning a1and a2, and secondary tuning ϵ should be a feasible way to avoid complexity. In this paper, ϵ is used as the tuning parameter, since this physical parameter directly influences how much fuel is injected immediately into the current cylinder.As shown by the equation (8), increasing the value of ϵ can cause more fuel mass injected into the current cylinder during the first a few cycles and also increase the deposited fuel in the wall which is inlet to the cylinder with delay.In this case,this delayed fuel injection may cause much speed regulation time.Based-on this observation,the logic for fuel injection tuning can be described as shown in Fig.5.It should be noted from Fig.5 that the parameter tuning is by online during a starting process. In this work,the error of the speed response to the speed reference,denoted as δ:=|ω-ωref|,is taken as the tuning index.

Fig.5 Flowchart of auto-tuning algorithm.

Finally, it should be noted that the proposed autotuning algorithm is the first step for the control design.The flow chart shown in Fig.5 suggests that the tuning process might be conducted by an extreme seeking or learning algorithm by minimizing a cost function J,such as

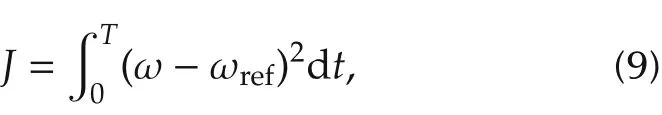
where T denotes a given finite time variable.

4 Simulation validation

Combining the control laws for the throttle opening and the SA in the previous work [7], the redesigned control scheme is evaluated by the provided simulator from the SICE benchmark problem.The simulator is constructed mainly by a 46th-order model which is oriented to industrial development. More detail introduction of the inside on the simulator is referred to the[1,10].

In the validation simulation, the reference starting speed is set as ωref= 750 r·min-1. The open-loop observer based fuel path control loop in the control scheme presented in [7] is replaced by the new control algorithms(5)and(8)as shown in Fig.6.

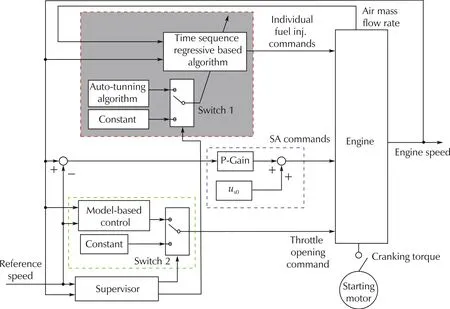
Fig.6 Block diagram of modified control scheme.

With the tuning policy in Section 3.2,the fuel injection control law is tuned as follows:

1)During the first cycle, the fuel injection command is delivered serially with an identical value, while from the second cycle, quite different injection commands are applied to the fuel path of each cylinder;

2) the parameters of algorithm (5) is chosen as a1=0.1089 and a2=0.752×10-8;and

3)the parameters of control law(8)are set as χ=0.01 and ϵ0=0.13.

Figs.7-9 show the simulation result. The air charge estimation by the control law (5) is as shown in Fig.7,and Fig.8 provides the individual fuel injection commands by the controller (8) and the responses of the fuel path in terms of the in-cylinder A/F.Especially,from the starting speed response curves shown in Fig.9 with three different ϵ values,it can be observed that the influence of the parameter ϵ to the regulation performance.Bigger ϵ leads to a longer regulation time as mentioned above.

Fig.7 Air charge estimation by the control law(5)(ϵ=0.1).

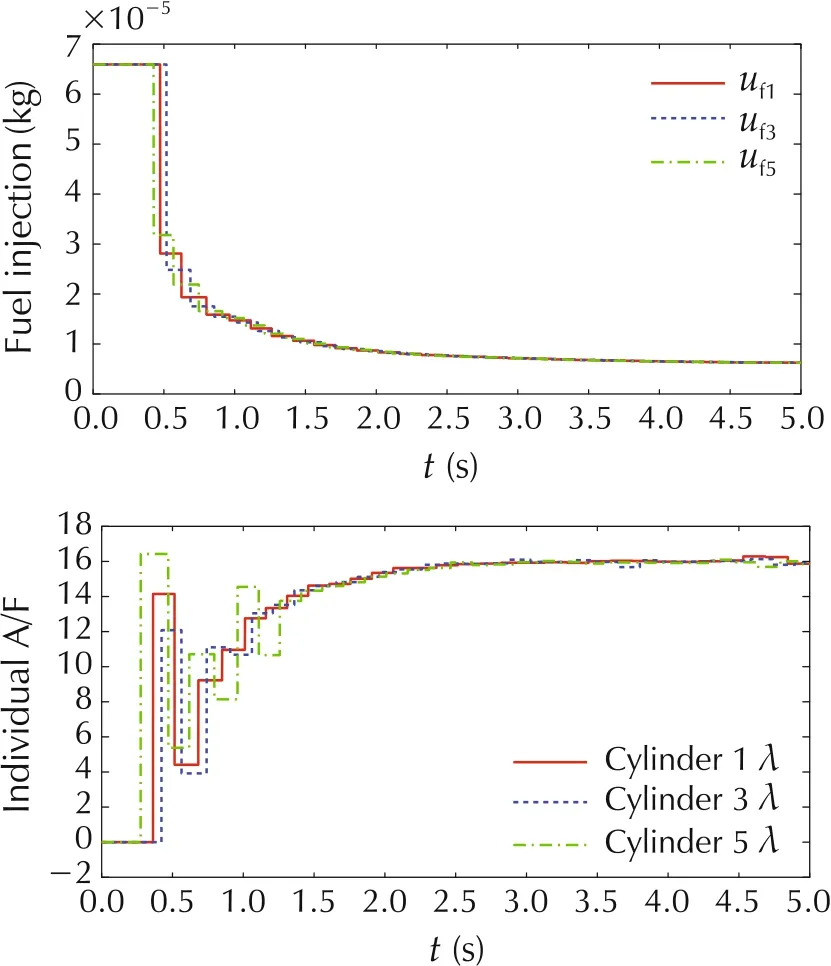
Fig.8 Fuel injection and the individual A/F curves(ϵ=0.1).

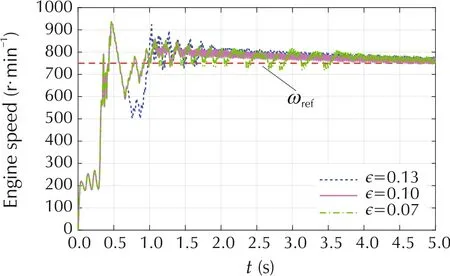
Fig.9 Starting speed response.

5 Conclusions

During the starting operation, thermal environment and dynamical characteristics of the air path and the fuel injection path of gasoline engine change dramatically,especially,before and after a cylinder getting successful firing. Furthermore, randomly stopped piston position causes the initial position of the crank angle uncertain and the stochastically getting firing of in-cylinder gas makes modeling the behavior of engine starting difficult.This paper recalled the model-based design approach for the SICE benchmark problem of engine starting control.Mainly,a time sequence regressive based fuel injection decision algorithm is proposed to replace the fuel injection control loop of the previous scheme.Combining with the parameter tunning procedure, the validation with the SICE benchmark simulator demonstrates that a solution that guarantees the response performance closed to the previous solution is achieved. The benefit of the modified scheme is that the control design is independent on the system model, and the control parameter tuning policy suggests to use learning or extremal seeking methods.This issue will be remained as the future challenge.