基于TSOA定位原理混合算法的掘进机位姿检测方法

刘 超，符世琛，成 龙，刘 丹，沈 阳，吴 淼

(中国矿业大学(北京) 机电与信息工程学院，北京 100083)

智能化开采成为煤炭安全高效开采的发展方向与必然趋势[1]。无人采掘装备是当前国际煤炭领域的发展前沿[2]。在地下巷道掘进过程中，传统掘进方法效率低，精度有限，而且井下矿工长期处于高温、高湿、高浓度粉尘环境，健康严重受损，井下环境复杂，事故频发，增加了矿工的工作强度及危险性，因此我国亟待研制无人采掘装备[3]。要实现综掘工作面的无人化，综掘装备自主导控是其关键，掘进机的位姿检测方法是实现综掘装备自主导控的核心，具有重要的研究意义。

智能化开采成为煤炭安全高效开采的发展方向与必然趋势[1]。无人采掘装备是当前国际煤炭领域的发展前沿[2]。在地下巷道掘进过程中，传统掘进方法效率低，精度有限，而且井下矿工长期处于高温、高湿、高浓度粉尘环境，健康严重受损，井下环境复杂，事故频发，增加了矿工的工作强度及危险性，因此我国亟待研制无人采掘装备[3]。要实现综掘工作面的无人化，综掘装备自主导控是其关键，掘进机的位姿检测方法是实现综掘装备自主导控的核心，具有重要的研究意义。

自20世纪90年代以来，国外主要产煤大国多以露天矿为主，在井下实际运用掘进机位姿检测技术的报道较少，多数技术集中在盾构掘进机中[4]。日本GYRO系统[5]使用陀螺仪检测盾构掘进机的姿态角，环境温度的变化对陀螺仪的机械有较大影响，该系统实用性不佳，只能作为人工测量的辅助参考。德国艾柯夫公司[6]的掘进机具有方向控制和自动成型以及对故障监控的功能，但位姿检测精度不高，受环境影响较大，在矿井中未见成熟应用案例。

近年来，国内学者对掘进机的位姿检测方法进行了许多研究。陶云飞[7]提出了一种基于激光导向系统的位姿测量方法、周玲玲等[8]提出了一种基于双激光标靶图像识别的位姿检测方法、童敏明等[9]提出了一种多传感器的定位系统、杜雨馨等[10]提出了一种基于机器视觉的位姿检测系统、贾文浩等[11]提出了一种基于iGPS的掘进机定位系统、吴淼等[12]提出了一种基于空间交汇测量技术的位姿自主测量方法、黄东等[13]提出了一种基于视觉/惯导的位姿测量方法。从上述研究可以发现，目前掘进机的位姿检测方法主要有:惯性导航、机器视觉、激光、全站仪、无线电等。不同的定位方法定位精度也各不相同，惯性导航[14]由于导航信息经过积分产生，所以定位误差随时间增大，精度差;基于激光、机器视觉的定位环境适应性较差，巷道中粉尘较大，会干扰可见光及红外线的传播，对成像会产生严重的影响;基于全站仪的定位需要专业测量人员参与，巷道环境复杂，增加了全站仪的工作难度;无线电定位主要包括WiFi、Bluetooth等，但上述方法精度不高，而超宽带(Ultra-wideband,UWB)测量范围广、系统组成简单、抗干扰能力强，局域范围内具有高精度测距功能，在掘进机静止或者移动过程中均能提供较高的定位精度。基于UWB测距，符世琛等[15-16]提出了一种基于TOA定位原理的掘进机自主定位定向方法，但该原理需要保证基站和终端的时基必须是同步的，同时该原理存在位置模糊解[17]，影响精度。

笔者基于UWB测距，根据TSOA定位原理，提出了一种面向掘进机的混合算法的位姿检测方法，建立了观测方程组，详细地推导了混合算法的计算过程;基于MATLAB仿真对比了间接法和混合算法的定位点空间分布、三轴误差及均方根误差，分析了混合算法的姿态角精度，在模拟巷道进行了实验验证，代入混合算法得到三维坐标，与标定值进行对比，得到了误差随距离变化的规律。

1 面向掘进机的超宽带位姿检测系统

1.1 UWB定位技术

UWB测距[19]是利用纳秒甚至皮秒级的极窄脉冲来实现信息的传输，UWB信号的相对带宽必须大于0.2，绝对带宽大于500 MHz，具有恒定的波达时间分辨率，可解算出准确的测距信息。它具有抗干扰能力强、多径分辨能力强、系统容量大、传输速率高、安全性高、成本低和功耗低等优点。

通过UWB信号无线电波[20]，测量目标的方向、距离、距离差等定位参量，实现位置坐标求解，定位过程如图1所示。利用UWB测距进行掘进机的位姿检测，关键是获得掘进机机身定位点的坐标。首先由一个或多个位置已知的基站发射无线电信号，无线电信号的电参量(如振幅、频率、相位、时间等)中的一个或多个携带着定位参量信息，经电波传播到PC端;其次PC端接收并处理该无线电信号，并根据电波传播特性，由电参量得到定位参量(如来波方向、距离、距离差、高度等);再次根据得到的定位参量及位置已知的基站，获得多个相对于各基站的位置面;最后由多个位置面根据相应的定位算法，得到掘进机机定位点的坐标。

图1 UWB定位结构Fig.1 Ultra-wideband positioning structure

1.2 TSOA定位原理

测距和定位(Time Summation of Arrival，TSOA)原理[20]是基于波达时间和，通过信号同步网络实现在时域、频域、空域上的严格同步，各站将测得的目标数据通过数据传递网进行传递，发射站只发射信号，接收站通过接收待测目标反射的发射站信号，测量从发射站到待测目标以及待测目标到接收站的距离和。在一个特定空间，保持与两个指定基准点距离和相等的点的轨迹是以接收站、发射站为焦点的椭球面，该面称为椭圆球位置面。在测量没有误差的情况下，UWB测距模块一旦得到接收站和发射站的距离和P，那么待测目标一定在由P所确定的椭圆球位置面上，其定位原理如图2所示。

设定4个定位基站A，B，C，D，基站A为发射站，只发射信号，其位置坐标为(XA,YA,ZA)，基站B，C，D为接收站，只接收信号，其基站群位置坐标为(Xi,Yi,Zi)，其中i=B,C,D。接收站通过接收目标反射的发射站信号，测量从发射站到目标的距离rA，以及目标到接收站的距离ri。掘进机的机身节点E的位置坐标为(XE,YE,ZE);第i个接收站获得的观测量为Pi，解算出3个椭圆球的交点，得出目标点的坐标值，则机身定位点位置坐标的TSOA观测方程组为

(1)

式中，

2 基于间接法与Taylor级数展开法的混合算法

位置坐标的解算方法有很多种，但是无论采用哪种方法均需求解非线性方程。方程(1)就是非线性方程组，然而在工程实现中，求解非线性方程并不是一件容易的事，同时，UWB测距存在一定的误差，测距误差的引入会导致椭圆球位置面不相交于一点或者根本没有交点。综上所述，对掘进机机身的定位问题就由原来的非线性方程精确求解问题转换成非线性优化的最优估计问题。

间接法与Taylor级数展开法各有优缺点，二者都是将非线性问题转化为线性问题。间接法可以通过直接计算得到一个初始点坐标，性能稳定。Taylor级数展开法为了防止收敛到局部最优点以及减少迭代次数，初始点的估计值需要靠近真实值，但在实际中不易实现，虽然一般都能收敛到真实点，但迭代过程的收敛性无法保证，同时每一次迭代都需要对矩阵求逆，运算量大。而由间接法得到的定位点估计值可以解决初始点这一问题，满足Taylor算法对初始点的要求，文献[18]表明Taylor级数算法的精度高于间接法。因此，在本文中提出了将间接法与Taylor级数展开法进行混合，通过间接法得到初始点坐标值后，代入Taylor级数展开法进行循环迭代消除误差，从而可以得到更精确的掘进机机身位姿。

2.1 间接法

在间接法中，首先把rA看成一个已知量，从而解得XE,YE,ZE是rA的线性函数，求出机身定位点E的坐标估计值，具体过程如下:

通过对方程组(1)进行移项，平方，整理化简，得

(2)

式中,

将式(2)转化为矩阵形式:

AX=b

(3)

式中

使rank(A)=3，由此可得最小二乘解为

X=(ATA)-1ATb

(4)

可得机身定位点E的坐标估计值为XE,YE,ZE。

2.2 混合定位算法

Taylor级数展开法是一种基于Taylor级数展开的加权最小二乘估计迭代算法，其核心思想为:首先在目标位置的初始估计点利用Taylor级数展开，并忽略二次及以上项，将非线性方程变为线性方程，采用最小二乘法对三轴偏移量进行估计;然后利用估计的偏移量对初始坐标进行修正，不断迭代，使估计的目标位置逼近真实位置，从而得到对目标位置的最优估计，混合算法程序流程图如图3所示。算法步骤主要如下:

(1)将式(4)中计算得到的(XE,YE,ZE)作为E点的初始估计坐标值，与真值(XE0,YE0,ZE0)的误差设为(δX,δY,δZ)，则有

(5)

(2)将式(1)在(XE,YE,ZE)点用Taylor级数展开，并忽略二次及以上项，则有

(6)

将式(6)转化为矩阵形式，则有

Αδ=Ζ

(7)

图3 混合算法程序流程Fig.3 Hybrid algorithm program flow chart

可得到δ的最小二乘解为

δ=(ATA)-1ATZ

(8)

(3)判断选择的判据ε是否小于给定的门限ε0，其中ε=δX+δY+δZ，设定ε0=0.1，若ε大于门限，则用式(9)代替对目标的上次估计值，并重复步骤(2)，(3)。

(9)

(4)若ε小于门限，则停止迭代，定位点E的最终估计位置为XE1,YE1,ZE1。

(10)

3 混合算法精度分析

3.1 定位点分布

为了探究定位点的分布，设定基站坐标A(0，10，0)，B(2，5，0)，C(-2，5，0)，D(2，0，5)，E点为掘进机机身定位点，坐标为(0，n，0)。采用美国Time domain公司生产的P440 UWB测距模块，宽带为3.1～5.3 GHz，中心频率为4.3 GHz，经过课题组的大量实验验证[21-22]，该模块在100 m狭长封闭空间的误差基本都小于0.02 m，在视距传播的条件下的测距参量一般呈现高斯分布，因此将均值为0、标准差为0.02 m的测距误差代入间接法和混合算法，得到定位点的三维坐标，并进行1 000次定位仿真，将仿真结果所得到的均值作为最终定位点的坐标值，n分别取15 m和90 m。

当n为15 m时，得到2种算法的定位点空间分布如图4所示。在间接法中，定位点在空间呈椭球状分布，定位点比较密集，三轴的误差可以达到厘米级，而在混合算法中，定位点在空间呈发射状分布，定位点发散，三轴的误差可以达到毫米级以上，相比间接法，精度有较为明显的提高。

图4 15 m定位点分布Fig.4 15 m positioning point distribution

对15 m这个定位点进行定位精度分析，在MATLAB中利用2种算法测量100次，得到如图5所示的三轴误差仿真曲线。在间接法中，最大误差在1 cm以内，Y轴误差较小，X轴、Z轴次之;在混合算法中，三轴的误差在毫米级以上，X轴误差较小，Y轴、Z轴无较大差异，该算法精度高于间接法。

当n为90 m，2种算法的定位点分布如图6所示。二者在空间中均呈椭球状，定位点比较密集，但混合算法的精度高于间接法，可达毫米级。

图5 15 m三轴误差仿真曲线Fig.5 15 m triaxial error curves

图6 90 m定位点分布Fig.6 90 m positioning point distribution

在90 m，用2种算法在MATLAB中对定位点测量100次，与真值比较，得到如图7所示的三轴误差曲线。由图7可知，间接法的误差基本维持在4 cm以内，Y轴误差最小，X轴、Z轴误差无明显差异，而混合算法三轴的误差达毫米级以上，Y轴误差最小，混合算法的精度有较大提高。

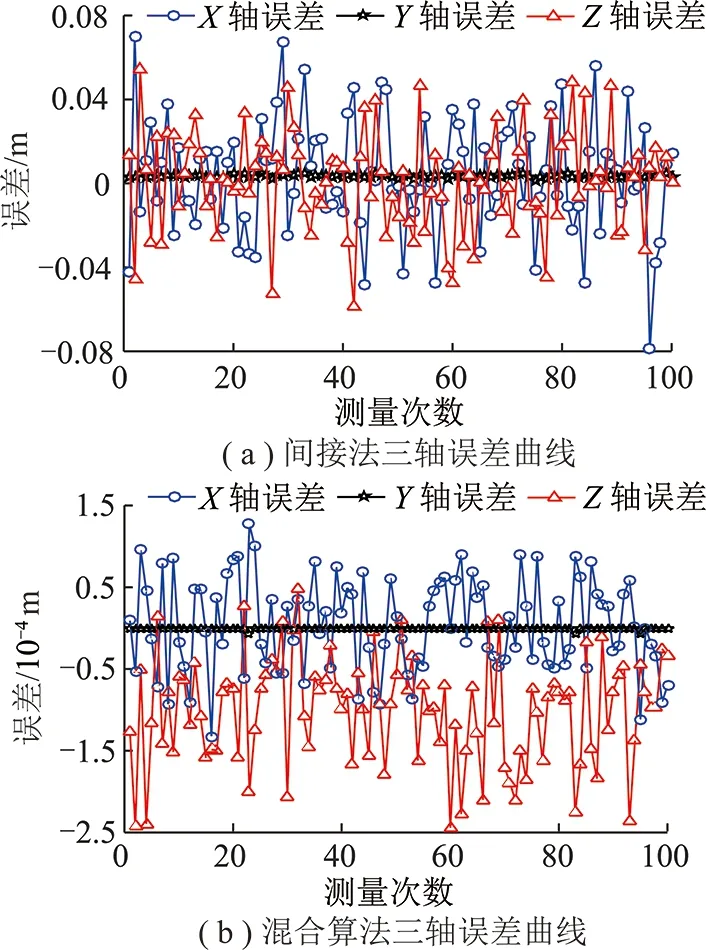
图7 90 m三轴误差仿真曲线Fig.7 90 meter triaxial error curves

3.2 均方根误差分析

在定位过程中，无论何种定位方法，由于受测量设备和传播环境的影响，测量的定位参量都会存在误差，从而导致定位误差的存在，并且采用不同的定位算法，定位误差的大小也不一样。均方根误差[23]是评价定位精度的一个十分重要的指标，均方根误差越小，定位精度越高，因此此处采用均方根误差作为定位算法精度的评判指标。

选取3.1节中的基站坐标，E为定位点，坐标为(0，n，0)，n从10 m处开始，每隔1 m移动一次，直到移动到100 m处，在MATLAB中根据2种算法对其进行仿真，得到2种算法的均方根误差随距离的变化曲线如图8所示。由图8可知，在10～100 m内，间接法的均方根误差控制在4.5 cm 以内，随着距离的增大均方根误差也在增大，而在混合算法中，均方根误差达到毫米级以上，相比间接法，精度明显更高。

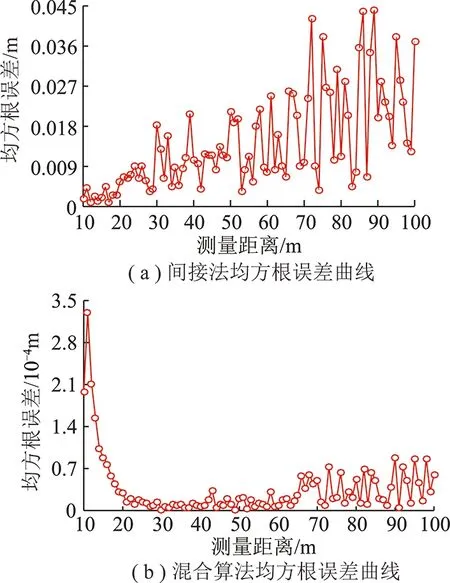
图8 均方根误差随距离变化曲线Fig.8 RMSE error curves with distance

为了探究三轴的定位精度随定位距离的变化关系，在MATLAB中进行仿真模拟，得到三轴的均方根误差随定位距离的变化曲线如图9所示。由图9可知，10～100 m内，在间接法中，三轴均方根误差随测量距离增大而增大，Y轴的均方根误差较小，在5 mm以下，X轴和Z轴次之，没有明显差异;在混合算法中，三轴的均方根误差达到毫米级以下，X轴和Y轴均方根误差较小。

图9 三轴均方根误差随距离变化曲线Fig.9 Triaxial RMSE error curves with distance

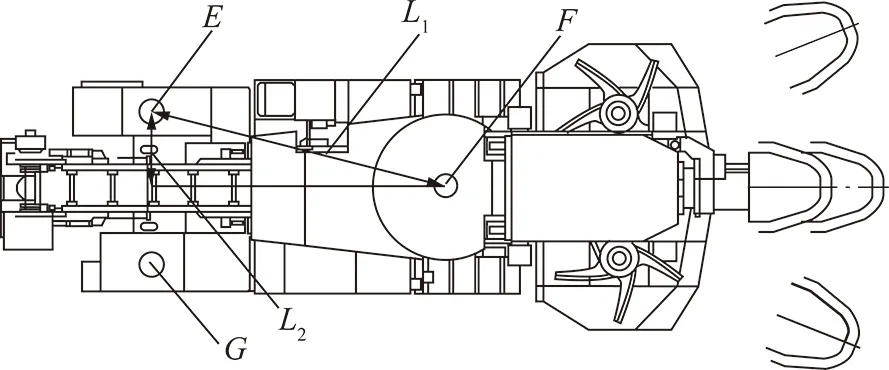
图10 掘进机机身定位点布置Fig.10 Layout of the roadheader fuselage locating point

由2种算法的定位点均方根误差曲线和三轴均方根误差曲线可知，混合算法的均方根误差可达到毫米级以上，精度明显高于间接法。

3.3 姿态角精度分析

图10为掘进机机身定位点布置示意图，3个定位点布置在同一水平面上，形成一个等腰三角形，掘进机机身视为一个刚体。结合EBZ160悬臂式掘进机的尺寸，图中L1为定位点E到定位点F的距离，L2为定位点E到掘进机中轴线的距离，定位点E到定位点G之间的距离为2 m，定位点F到L2之间的距离为2 m。

4个基站的坐标与3.1节中相同，基站对机身的3个定位点E，F，G进行测距，利用混合算法解算出定位点的坐标，代入位姿解算公式[16]，可得到掘进机的航向角α、俯仰角β、横滚角γ。

(11)

分别选取15 m和90 m进行位姿参数精度分析。在15 m中，E(1,13,0)，F(0,15,0)，G(-1,13,0)，90 m中，E(1,88,0)，F(0,90,0);G(-1,88,0)，可得到如图11所示的位姿参数精度分布曲线。由图可知，在15 m处，掘进机的航向角、俯仰角、横滚角的精度可达到0.005°左右，其中航向角精度最高;在90 m处，各姿态角的精度可控制在0.008°以下。随着定位距离的增大，定位误差也随之增大，同样，位姿误差也随着定位距离的增大而增大。

图11 位姿解算精度曲线Fig.11 Accuracy curves of pose

4 实验验证

煤矿的巷道可近似为狭长封闭空间，实验选择在与巷道相似的狭长封闭的楼道中进行，二者在其空间变化上是相似的，重点研究该位姿检测系统及其算法的精度，以及空间结构对UWB模块的影响。采用的UWB测距模块是美国Time domain公司生产的P440模块。准备工作如下:

(1)在电脑上安装P440测距软件。

(2)将模块1，2，3，4(端口ID:101，102，103，104)连接至PC端，运行软件并调至ALOHA组网模式，将4个模块设置为基站。

(3)将模块5，6，7(端口ID:105，106，107)连接至电脑，运行软件，将软件调至ALOHA组网模式，将3个模块设置为动点，断开连接。

(4)将1，2，3，4模块用数据线接入USB分线器，连接至PC端。

(5)放置三脚架，将模块1，2，3，4分别固定在4个三角架的云台上，摆放好位置，用重锤线标定天线相位中心位置，便于确定坐标位置，用激光测距仪测量4个模块的三维坐标，坐标见表1。

表1 模块坐标Table 1 Coordinates of modules

(6)在前方放置一张桌子，模块5，6，7安装在手机支架上，将手机支架固定在桌子上的3个角，形成一个直角三角形，确保高度一致。模块位置示意如图12所示。

(7)给模块接入移动电源，确保模块供电。

实验步骤:

(1)用激光测距仪测量模块1，2，3，4的三维坐标，以及模块5，6，7到模块1，2，3，4天线基准点之间的距离并记录。

(2)在电脑上运行P440测距软件，模块1，2，3，4设置为广播模式，时间间隔设置为100 ms。

(3)在logging窗口选择保存数据的文件夹。

(4)返回测距窗口，点击“send”按钮启动模块发送电波开始测距，数据以Excel文件形式自动保存在刚才选择的文件夹中。

(5)将模块5，6，7向前移动，保持3个模块之间的相对距离不动，间隔一定距离再次重复以上步骤并记录。实验实物如图13所示。

图13 定位实验实物Fig.13 Photograph of the experiment for positioning

在3～94 m内，根据UWB模块所测模块5，6，7到模块1，2，3，4的测距信息，利用混合算法计算模块5，6，7的位置坐标，相关数据见表2，3，4。

表2 模块5测量数据Table 2 Measured data of module 5

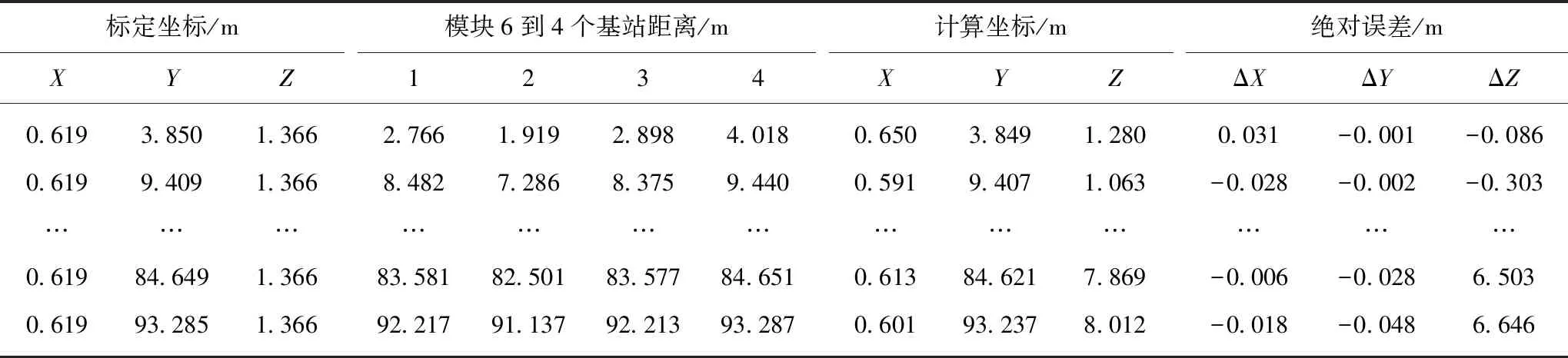
表3 模块6测量数据Table 3 Measured data of module 6

将定位模块5，6，7的标定坐标与计算坐标相减得到绝对误差，对三轴误差在 MATLAB中进行拟合得到误差随距离变化的误差曲线，如图14所示。由图14分析可知，基于混合算法在3～94 m的测量范围内，X轴和Y轴在30～50 m处出现了峰值，这是由于该位置楼道环境发生了变化，成为空旷非封闭环境(图12)，导致UWB的传播路径发生变化，从而出现了多径效应[21]，因此误差较大。其中Y轴精度较高，在测量范围内可达到毫米级，且不随测量距离的增大而增大，X轴方向误差基本控制在4 cm以内，Z轴方向误差随测量距离的增大而增大，在94 m附近误差高达6.763 m。由此可知，在3～94 m测量范围内，X轴和Y轴可以满足掘进机的定位要求。

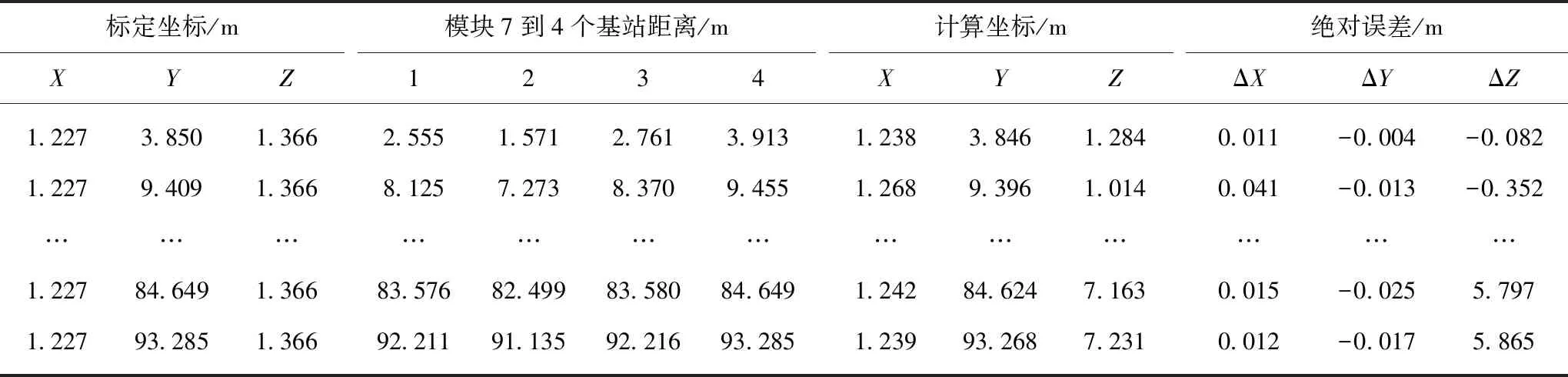
表4 模块7测量数据Table 4 Measured data of module 7

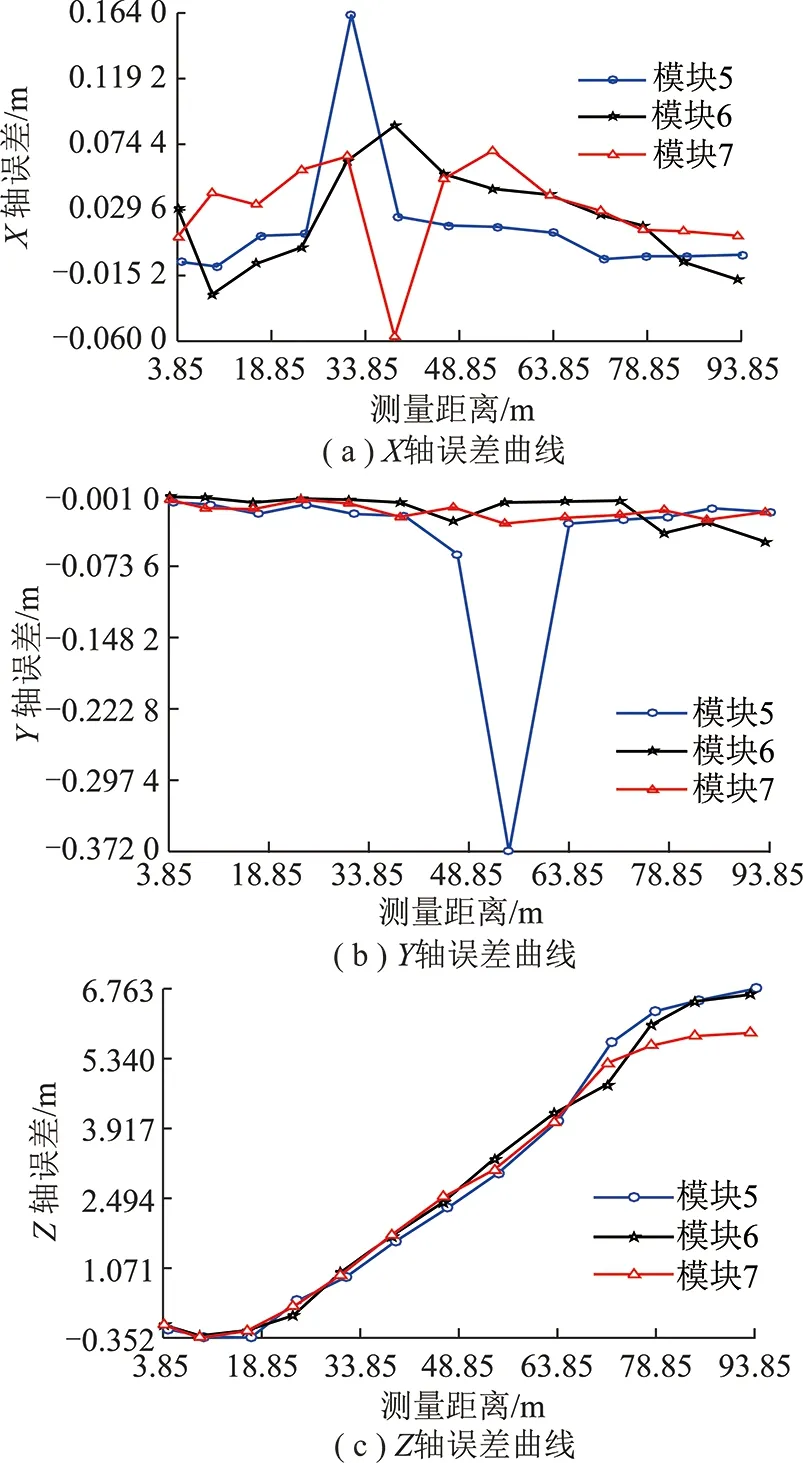
图14 模块5，6，7的X,Y,Z轴误差曲线Fig.14 X,Y,Z xial error curves of module 5,6 and 7

5 结 论

(1)基于UWB测距，根据 TSOA定位原理，提出了一种面向掘进机的混合算法的位姿检测方法，建立了观测方程组，系统地推导了混合算法的计算过程，将间接法计算得到的初始值代入Taylor级数展开法，循环迭代，消除误差，最终得到了掘进机机身的三维坐标。

(2)基于MATLAB对间接法和混合算法进行了定位仿真实验，仿真对比了2种算法的定位点空间分布、三轴误差、均方根误差以及姿态角，由仿真结果可知:混合算法的精度优于间接算法，在10～100 m的测量范围内，间接法的各轴精度可达到厘米级，Y轴精度较高，均方根误差可控制在4.5 cm以下，而混合算法的各轴精度可以达到毫米级以上，均方根误差在毫米级以上，姿态角的精度可以控制在0.008°以下。

(3)搭建了掘进机位姿检测实验平台，开展了模拟巷道的UWB测距实验，完整地采集了实验的相关数据，将所测数据代入混合算法得到掘进机的三维坐标，与标定坐标比较，得到了误差随距离变化的规律。实验表明:在3～94 m的测量范围内，X轴误差基本控制在4 cm以内，Y轴误差可达毫米级以上，Z轴误差较大，随测量距离的增大而增大。在三维空间中提高Z轴精度的方法值得继续研究。