基于方位/频率测量的悬浮式深弹炸点控制研究

陈韶华,刘天华,汶宏刚,罗会彬

(1.中国船舶重工集团公司第七一〇研究所;2.海军驻宜昌地区军事代表室,湖北 宜昌 443003)

0 引言

深弹是一种重要的反鱼雷武器。悬浮式深弹在舰艇一定距离上形成对鱼雷的拦截屏障,其作战效能的发挥,关键在于深弹对鱼雷的可靠探测和炸点精确控制[1-2]。

深弹对鱼雷探测有主动和被动2种方式,主动方式要求的探测系统结构复杂、成本高,被动方式对系统要求相对简单。被动方式又分2种方法:接收鱼雷辐射噪声,接收鱼雷自导信号。现代高性能鱼雷一般采用线导+声自导方式,只在距目标很近时才开启主动声自导,因此可能存在深弹接收不到鱼雷声自导信号的情况。鱼雷辐射噪声是比较稳定的噪声源,尽管随着鱼雷减震降噪技术的发展,鱼雷辐射噪声有所下降,但在深弹探测的近距离范围内,仍有可能满足深弹的探测定位和炸点控制要求。

文献[3]通过线谱相位变化率来测量目标距离变化率,但不能得到具体的距离值。本文采用矢量水听器接收鱼雷辐射噪声,通过检测其中的线谱频率和方位变化,采用TMA方法估计目标的航速、航向、距离和通过正横时刻,在该时刻前发出起爆信号引爆深弹摧毁鱼雷。

1 矢量水听器对鱼雷线谱的检测与定向原理

典型鱼雷辐射噪声线谱主要分布在100～1 000 Hz之间,在1～5 kHz之间也有较强的宽带能量与线谱分布。

二维压差式矢量水听器可以安装在深弹头部用于探测鱼雷辐射噪声。如图1所示,组成压差式矢量水听器的声压水听器1和2、3和4分别位于空间笛卡儿坐标系相互垂直的x轴与y轴上,它们之间的间距均为d,声中心在观测点o处。

图1 二维压差式矢量水听器示意图Fig.1 Schematic diagram of two-dimension pressure difference vector hydrophone

压差式矢量水听器声压由4个声压水听器平均得到:

振速由声压梯度积分得到[4]:

式(2)与式(3)在时间轴上滑动进行运算,就得到vx(t)与vy(t)。

对声压与振速信号p(t)、vx(t)、vy(t)分别做FFT,得到P(f)、Vx(f)、Vy(f)。采用互谱法得到水平声强的2个分量[5]:

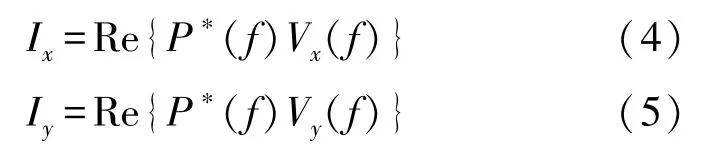
于是可得到频域声强的幅度和方向:

通过式(6)声强谱可以进行线谱检测,式(7)估计线谱的方向。矢量水听器声强检测与方位估计示意图如图2所示。

图2 矢量水听器检测与方位估计示意图Fig.2 Schematic diagram of detection and bearing estimation with vector hydrophone

2 鱼雷正横位置的预测

对上述矢量水听器获得的目标辐射噪声的声强谱,采用线谱的自动检测与提取方法[6]检测线谱,估计线谱频率与方向,得到鱼雷从悬浮式深弹附近经过时的频率、方位序列(n)和(n),采用TMA方法估计目标的航速、航向与位置参数。

2.1 目标观测模型

假设鱼雷从深弹附近匀速直航通过,以悬浮式深弹为中心建立坐标系,如图3所示。

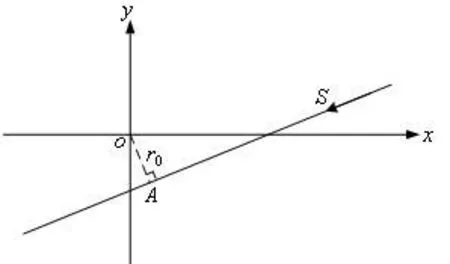
图3 目标运动态势Fig.3 Target motion situation

目标的2个速度分量表示为

式中:ux(n)与uy(n)表示与速度独立且相互独立的噪声扰动,服从零均值高斯分布N(0,);vx与vy在本节表示目标航速。

目标的位置表示为

式中T为采样间隔。

待估计的目标速度与位置写成状态方程,有:

简写为

观测点对目标方位与多普勒频率的测量由下式得到[7]:

式中:测量噪声wφ(n)与wf(n)体现了方位与频率测量误差,它们分别服从零均值高斯分布N(0,)与N(0,),且与x(n)、y(n)、vx(n)、vy(n)独立。为处理方便,也假设噪声相互独立。

式(11)简写为测量方程:

可以看出观测量与状态量之间是非线性关系,需采用扩展卡尔曼滤波器估计目标参数。对h(s(n))进行一阶泰勒级数展开,得到观测矩阵:

式中雅可比矩阵:

为了表达方便,上式x、y后的序号n省略。

2.2 扩展卡尔曼滤波器对目标的跟踪

根据文献[8],扩展卡尔曼滤波器写为

1)预测。

2)最小预测MSE矩阵。

3)卡尔曼增益矩阵。

4)修正。

5)最小MSE矩阵。

式中状态转移矩阵A由式(10)定义,其它参数定义如下给出。

状态噪声与观测噪声协方差矩阵分别表示为

观测数据θ(n)根据运动模型来估计,作为测量值输入。初值的设置包括噪声方差及采样间隔T,对跟踪性能都有很大影响,需要多次仿真与优化。

经过扩展卡尔曼滤波,估计出目标位置与速度参数x(n)、y(n)、vx(n)、vy(n),可以得到目标的航迹方程:

式中:k=vy/vx为直线斜率;y0通过把目标位置x(n)、y(n)代入上述方程求得。

目标正横位置是上述方程与其垂线方程y=-x/k的交点,于是可预测出鱼雷过正横时刻和正横距离。如果正横距离小于引信爆炸半径,在鱼雷接近正横位置时刻,控制深弹起爆。

3 计算机仿真

设鱼雷在坐标系中的初始位置为(500,200),航速为50 kn,航向-155°,可以计算出目标正横距离30 m。目标辐射噪声线谱频率为500 Hz,线谱谱级设为130 dB。6级海况条件下500 Hz噪声谱级约75 dB。采用矢量水听器检测到的线谱频率变化如图4(a)所示,频率分析分辨率为1 Hz,频率估计均方根误差为0.3 Hz。估计的目标方位如图4(b)所示,方位估计均方根误差为3°。

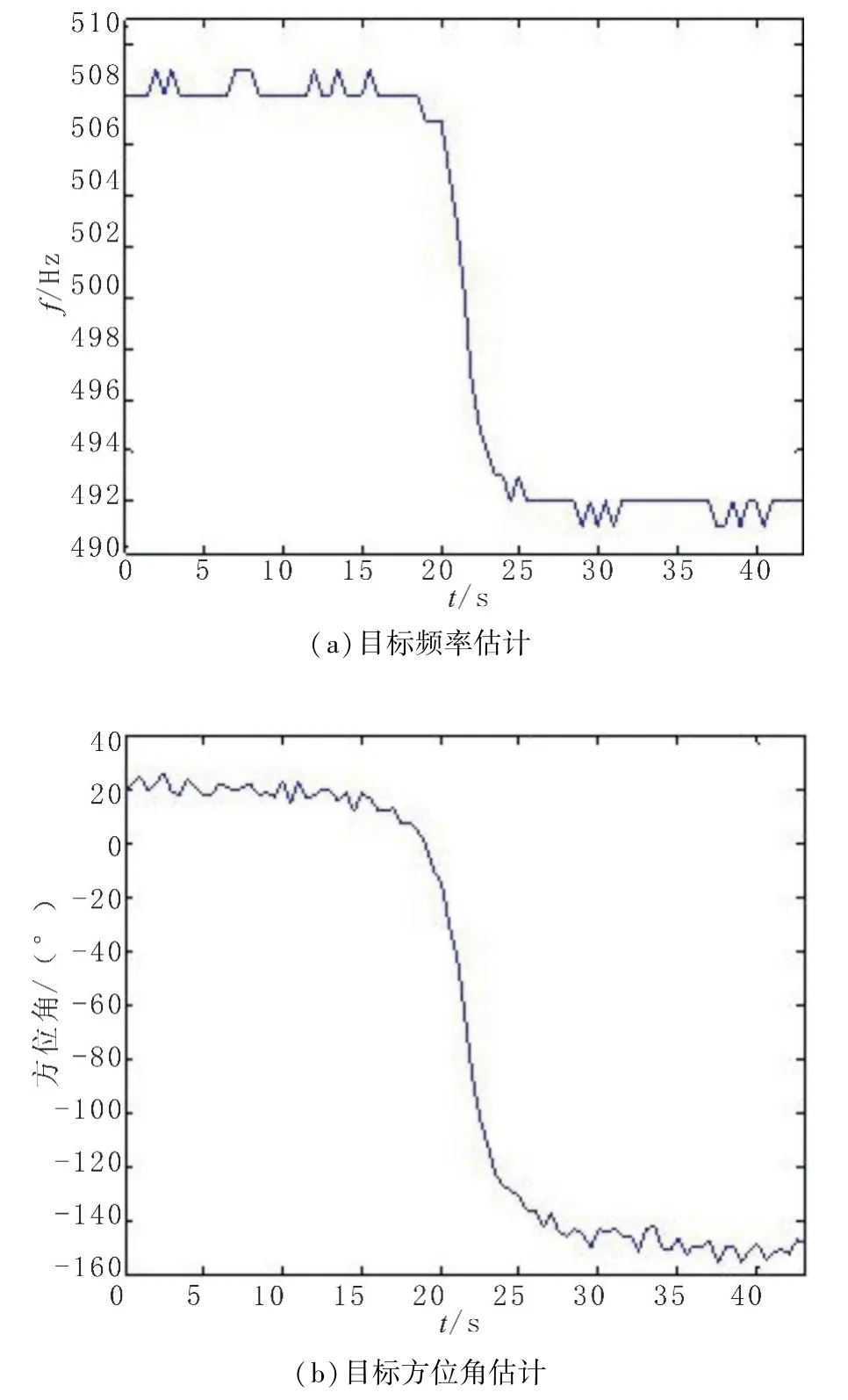
图4 鱼雷目标的频率与方位角估计Fig.4 Frequency and bearing estimation of torpedo target

图5是采用扩展卡尔曼滤波器估计的目标航迹和航速等参数。矢量水听器只能测向、不能测距,通过方位/频率TMA分析,可以得到目标的距离信息。可以看出,扩展卡尔曼滤波算法在不到10 s的时间内收敛,越接近正横,估计值误差越小。至正横前约3 s时,估计目标位置为(118.4,17.9),航向估计为-153°,航速估计为24.5 m/s。故航向估计误差2°,航速估计误差0.5 m/s。根据图3几何关系可计算出鱼雷过正横位置坐标为(12.7,-27.2),根据扩展卡尔曼滤波算法估计的正横位置坐标为(17.2,-33.7),距离误差为7.9 m,可以满足炸点控制的需要。

图5 鱼雷航迹与航速估计Fig.5 Trajectory and velocity estimation of torpedo

4 结束语

本文讨论了悬浮式深弹采用矢量水听器对鱼雷辐射噪声线谱的检测与测向,以及采用方位/频率TMA预测鱼雷正横距离从而控制深弹炸点的方法。对高速运动的鱼雷,线谱频率与方位有较大变化,能满足扩展卡尔曼滤波方法预测目标正横距离的需要。计算机仿真验证了方法的可行性。工程中,还应考虑本舰噪声对鱼雷辐射噪声检测的干扰。