AUV装备任务可靠度指标论证方法研究

韩守鹏,杨振宇

(中国人民解放军92578部队,北京 100161)

0 引言

武器装备通常用战备完好性、任务可靠性、维修人力费用和保障费用四方面的要求来规定系统的可靠性,以综合反映武器装备的作战效能以及用户费用要求。这些要求通常体现为基本可靠性、耐久性、贮存可靠性和任务可靠性四类参数[1-5]。其中前三类参数主要反映了装备对维修、保障资源的需求;任务可靠性则反映了装备在规定的任务剖面中完成规定功能的能力,为概率指标,与具体使用紧密相关,对AUV装备,该指标通常描述为任务可靠度。在进行AUV装备任务可靠度指标的论证时,既要考虑装备本身的技术能力对任务可靠性指标的支持,又要考虑装备使用的效费比需求。对技术能力方面的论证,已有相关文献研究可借鉴[6-8];对使用需求方面的论证方法,是从使用方的角度分析研究任务可靠度指标的合理性,但未查到相关系统性文献,这就是本文研究的主要内容。

1 任务可靠度指标论证的影响因素

对AUV这类一次性使用、或自主作业并返回的可重复使用装备,其采购、维护及所携带载荷的成本较高,从装备使用需求角度论证任务可靠度指标对研制或采购决策制定显得更加重要。考虑实际使用情况,提出了以下有关任务可靠度指标论证的使用需求影响因素。

1.1 平均作业完成次数

平均作业完成次数是指计划执行n次任务条件下,能够完成预定作业目的平均次数。

对于一次性使用的单程型任务,n=1,设p为单次任务可靠度,则平均作业完成次数即为p。

考虑往返型任务情况,在某些情况下,虽未成功返回,但也可能已经达到预计作业目的。令w为加权系数,表示未成功返回情况下,仍已达到预定作业目的的平均概率,其取值范围为[0,1),具体应根据装备和任务情况实际确定。据此,连续完成次作业目的的概率可表示为

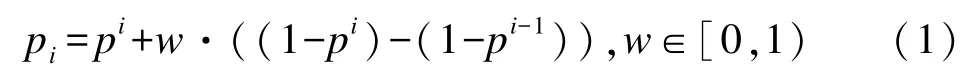
设计划执行任务总次数为n,则执行n次任务时,对应的平均作业完成次数为

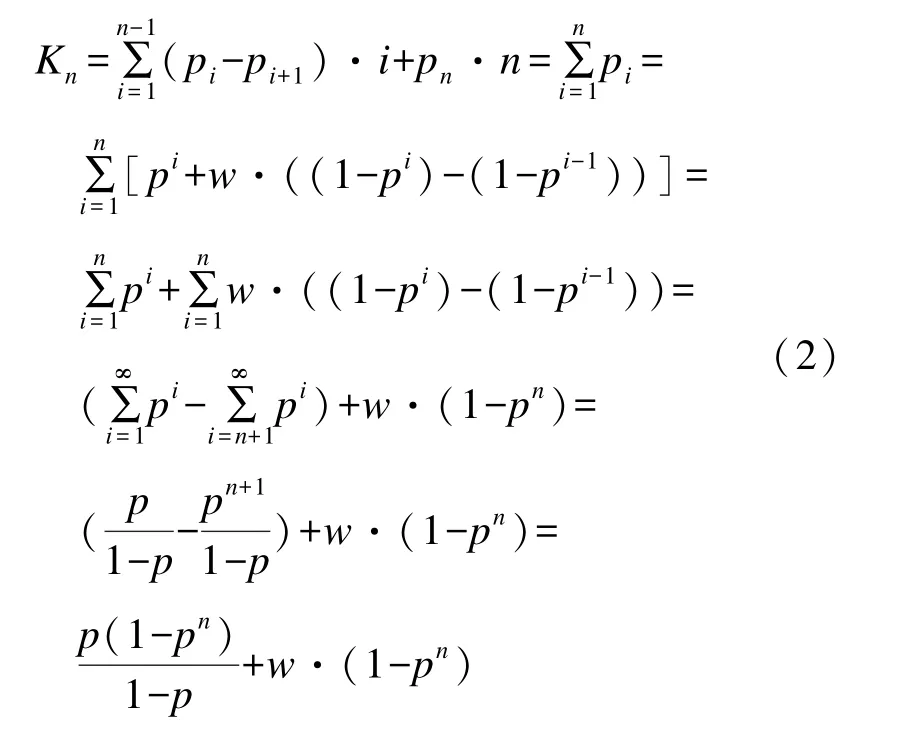
对于必须成功返回才达到任务作业目的的往返型任务,相当于前述分析情况的一个子集,对应于w=0。此时,可在前面分析基础上,进一步简化为

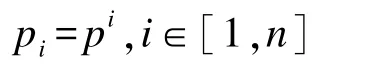
进一步有

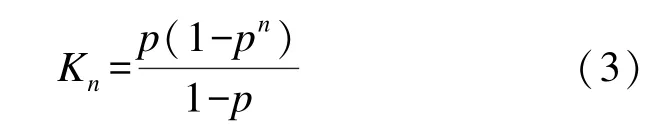
显然对于单程型任务,实际为往返型任务在n=1,w=0条件下的一个特例子集,即有

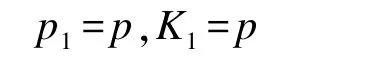
因此,本文后续讨论内容,均以往返型任务为对象展开。

1.2 平均任务寿命

从概率意义上讲,平均任务寿命为要求执行无限大次任务时,对应的平均作业完成次数,即

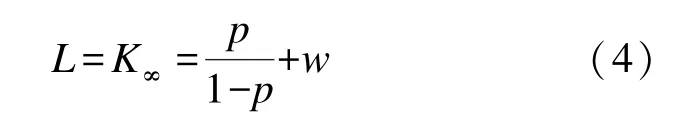
1.3 平均任务完成率

平均任务完成率是指平均作业完成次数与计划执行任务总次数平均任务完成率的比值,即

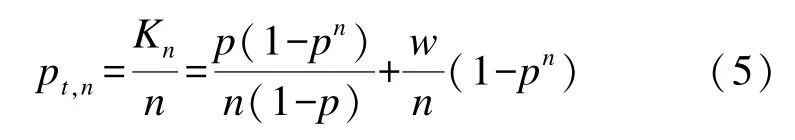
根据上式,w=0条件下,求解不同任务次数n、不同单次任务可靠度取值p条件下的平均任务完成率,结果如表1所示。

实际上,平均任务完成率是与需求的总任务次数紧密相关的,在实际使用或论证时,应结合需要完成的任务总次数及其对应的平均任务完成率要求,来综合考虑单次任务可靠度的指标需求。

1.4 完成任务所需最优储备条数

执行任务前,需规划确定完成任务所需最优储备条数M,以避免储备不足和储备过量情况的出现。其确定依据:M条同时参与任务时,完成有效任务条次数C(其取值由任务最终需要达到的效果决定)前提下,对应的平均任务完成率pt,n应达到事先规定的最低可接受值pt,min。根据这一思想,结合前述公式,推倒得出储备条数计算公式如下:

1)任务不受时间限制。

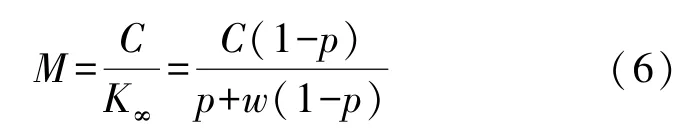
事实上,任务不受时间限制的情况是比较极端的,考虑任务受时间限制的情况更有意义。

2)任务受时间限制。

此时即对应为在规定时间内,完成规定有效任务条次C,平均任务完成率应达到预设概率值pt,min要求。

设单次任务执行时间为Δt,规定任务时间为T,则规定时间内单条最多执行任务次数为m,则m应满足:

其中floor为向下取整函数。则有:

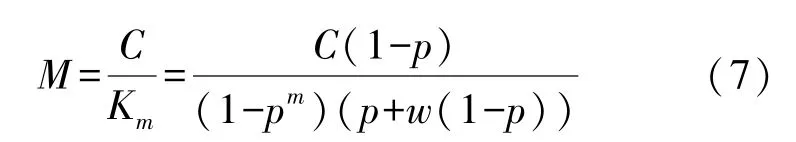
2 灵敏度分析

2.1 单次任务可靠度p对平均任务完成率pt,n的影响

根据公式(5),w=0条件下,有:

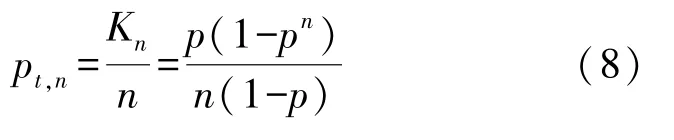
随着要求达到的平均任务完成率和任务次数的提升,所需的单次任务可靠度相应提升。任务次数的确定可考虑寿命次数、维修周期综合确定。例如,在连续任务执行次数不小于5次、平均任务完成率不低于0.6 的要求下,单次任务可靠度应不低于0.82,考虑适当余量,单次任务可靠度不低于0.85是必要的。

2.2 单次任务可靠度p对平均任务寿命的影响

根据公式(5),对应有:

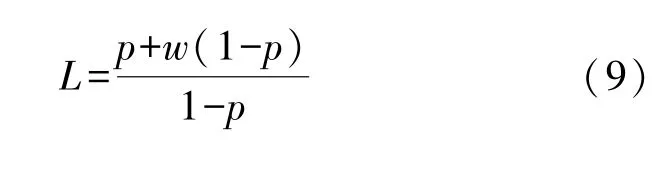
平均寿命是随单次任务可靠度的变化率单调增长的。针对几种单次任务可靠度的典型取值,在p=0.6,0.7,0.75,0.8,0.85,0.9,0.95时,对应的平均任务寿命为L=2,2.8,3.5,4.5,6.2,9.5,19.5次。

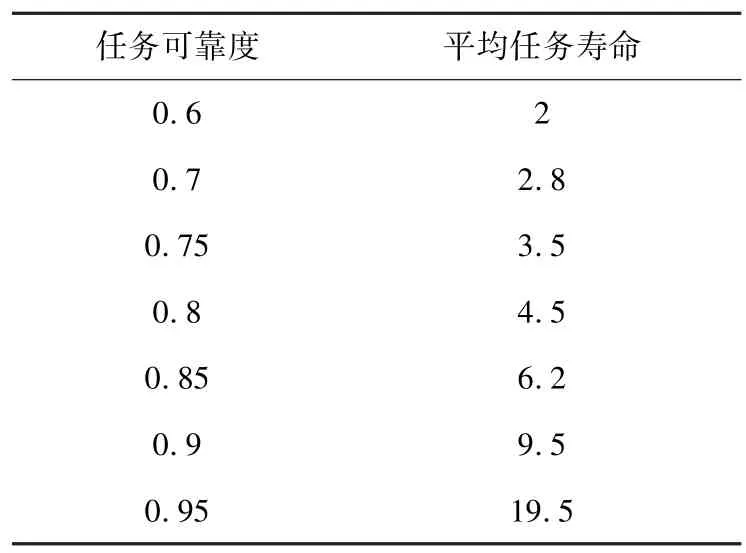
表2 不同任务可靠度对应的平均任务寿命Table 2 Average mission life of different mission reliability

进一步分析,平均寿命随单次任务可靠度的变化率为

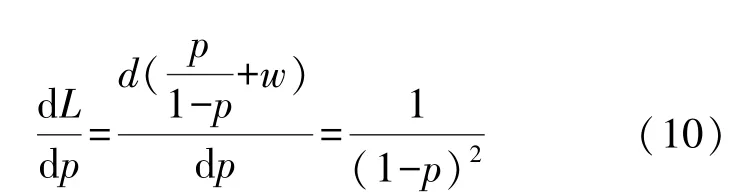
由此可见,平均任务寿命的变化率也是随单次任务可靠度单调增长的,因此,对于连续工作条件下的平均任务寿命,提高单次任务可靠度对于保证其预期指标值的实现是至关重要的。上述分析是针对平均任务寿命来说的,即对应于任务总次数需求为无穷大的情况。在实际使用或论证指标的过程中,可结合实际需要,保证一定平均任务完成率条件下的任务总次数。结合公式(2),对dKn/dp在某一范围内进行约束区间内的细化求解,但分析方法及其总体变化趋势及规律是类似的,可根据具体情况具体分析。

2.3 单次任务可靠度p对储备量的影响

根据需要完成的有效任务条次数,对应不同单次任务可靠度取值,在任务不受时间限制条件下,利用公式(6),得到最小储备数量需求与单次任务可靠度的关系如图1所示。从图中可以看出:对给定的单次任务可靠度,最小储备数量与需要完成的有效任务条次数呈近似线性比例关系,且线性系数随单次任务可靠度p取值的提高而降低。p∈[0.7,0.95]对于储备数量需求是一个变化比较明显的区间,如单次任务可靠度分别取0.7、0.95时,储备数量的差距在3倍以上;由公式(6)容易推导出dM/dp与1/p2成正比,储备数量增加的变化幅度随p的提高而逐渐减小,对dM/dp来说,p∈[0.7,0.9]仍是一个变化比较明显的区间。因此,在该区间内,提升任务可靠度对装备储备数量有着显著的影响。对于任务受时间限制条件下的储备量需求分析,可结合具体要求,用公式(7)代入计算,分析方法和变化趋势与上述类似。

另外,储备数量需求还应在上述最小储备数量确定的基础上,综合考虑执行任务、平时训练的损耗以及保障的完好率等因素,考虑一定的余量综合确定。

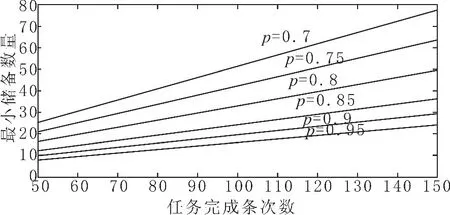
图1 最小储备数量需求随单次任务可靠度的变化Fig.1 Change of minimum reserve quantity requirement with single mission reliability

3 结束语

本文的主要思路是从军事和经济性需求的角度,基于任务需求和效费比要求,研究如何分析确定AUV装备的单次任务可靠度的指标需求问题。研究方法是把单次任务可靠度作为一个整体考虑;考虑到实际使用过程中,也可能存在返回但未达到预定作业目的(如因故未完成预定探测目的,但却成功返回)。此时整体任务可靠度统计中已属于失败范畴,但航行体并未损失,此时可以把整体任务可靠度分解为航行任务可靠度和作业动作任务可靠度。由于通常动作可靠度可以根据先验知识简化为一个固定值处理,因此仍可以按照文中所述的方法代入计算,得出航行可靠度和整体任务可靠度需求值。此方法具有普适性,但具体应用时可根据情况对任务可靠度进一步细化分解研究确定。

同时,任务可靠度指标的论证是一个综合性问题,应充分考虑需求牵引和技术驱动两方面因素的对接,采用自顶向下和自底向上双向结合的方法,综合考虑装备的整体效费比研究确定。本文提出的方法,适用于从战术需求、使用效费比出发,自顶向下推导出任务可靠度的整体指标或粗分解指标需求;而自底向上的论证[6],则需要细致分解系统组成,构建整体任务可靠度与分系统、组部件可靠度之间的关联关系。综合考虑技术可达性和效费比,优化给出技术可实现的整体任务可靠度以及各分系统的任务可靠度指标分配;在此基础上,根据装备需求,综合权衡使用指标、技术能力的匹配关系,最终确定任务可靠度指标。