直立式水下驻留平台座底稳定性分析

张 斌

(中国船舶重工集团公司第七一〇研究所,湖北 宜昌 443003)

0 引言

为更好地进行海洋开发研究,针对某一海域开展长时间定点监测或探测任务,实现诸如海洋水情勘测、海洋水质监测、海底土壤结构研究、水下建筑物与深海管道检测等具体功能,逐渐成为各国学者的研究重心并为之投入了大量精力。传统海洋工程中常用的AUV或ROV均存在自身缺陷,无法很好地完成此类任务要求[1-2]。

为解决这一现实问题,具有着陆驻留于海底这一特定功能的水下航行器被研制出来,这类水下平台自主航行至需要探测或监测海域后下潜驻留于海底,在驻留过程中依靠自身机构维持静态平衡,在不需要时刻调节航行器驻留姿态的条件下完成探测或监测任务。随着相关研究工作的开展,这些可实现驻留功能的水下平台逐渐在其专业范围内发挥出不可替代的作用,在人类深入开发海洋资源的过程中扮演着重要的角色。驻留于海底的水下平台在海流作用下不可避免地发生姿态与位置变动,其抗流稳定性关系到后续工作任务能够正常开展,必须对其进行重点分析。

根据水下驻留姿态的不同,可将其分为横卧式与直立式。两种方案各有优势,其中横卧方式具有更好的坐地稳定性,而直立式则在资源探测、环境监测及反潜作战等领域具有更高效率。目前,现有的水下驻留平台大多采用横卧方式下潜座底[3-5],对其座底稳定性分析大多将海底简化为刚性平面[6],具有较大的局限性。

本文针对竖直座底驻留水下平台特点,建立适合大攻角运动状态的海流响应运动模型,采用姿态四元数描述平台座底姿态以解决可能出现的数值奇异现象。基于弹性力学理论建立符合海底真实物理特性的弹塑性数值模型并将平台-海底交互作用融合进座底平台数学模型中,对驻留稳定性进行仿真研究,为实现水下平台可靠地直立驻留海底提供有意义的参考。

1 坐标系选取

为便于建立平台座底抗流过程中的运动学与动力学方程,描述海流冲击作用下的平台瞬时位置与姿态,引入以下直角坐标系[7]:

1)地面坐标系Exeyeze:坐标原点E可选在海底平面上,即ye=0处;Exe轴位于水平面内;Eye轴位于竖直面内,铅直向上为正;Eze轴的指向参照右手系规则确定,(ie,je,ke)为该坐标系3个轴向的单位矢量。

2)座底平台体坐标系Bxbybzb:各轴与座底平台固连,原点选在平台浮心B处。Bxb轴沿平台纵轴,指向前为正;Byb轴垂直于Bxb轴,当座底平台在地面上水平放置时,指向上为正;Bzb轴垂直于Bxbyb平面,其正向使Bxbybzb构成右手直角坐标系。

3)座底平台速度坐标系Bxvyvzv:原点与体坐标系原点重合,Bxv轴与原点处座底平台的速度矢量重合;Byv轴位于座底平台的纵对称面内,与Bxv轴垂直并指向上方;Bzv轴垂直与Bxvyv平面,指向按右手直角坐标系确定。

通常情况下,体坐标系下广义速度参数向量Vvehicle可以通过速度与角速度的投影转换矩阵得到与地面坐标系中广义位置参数向量Rvehicle的具体对应关系。

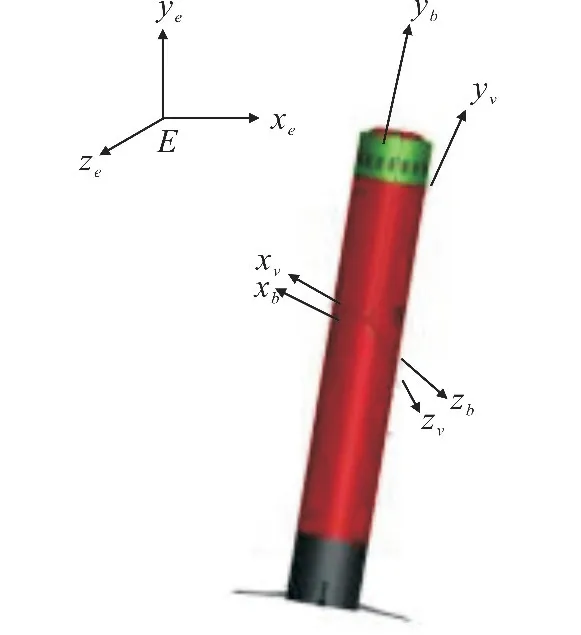
图1 坐标系示意图Fig.1 Schematic diagram of coordinate system

2 动力学与运动学方程

引入下列运动参数,包括地面坐标系中座底平台浮心位置矢量与姿态角共同组成的广义位置参数向量Rvehicle=[xe,ye,ze,θ,ψ,φ]T、由体坐标系下平台浮心速度矢量与角速度共同组成的广义速度参数向量Vvehicle=[vxv,vyv,vzv,ωxv,ωyv,ωzv]T,由体坐标系下平台所受的力与力矩组成的广义力参数向量Fvehicle=[Fxv,Fyv,Fzv,Mxv,Myv,Mzv]T。

基于平台浮心的动量与动量矩定理,可建立适用于直立式座底平台抗流工作状态的动力学方程[8]:

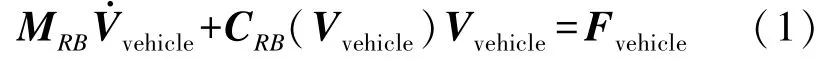
式中:Fvehicle为座底平台所受作用力;

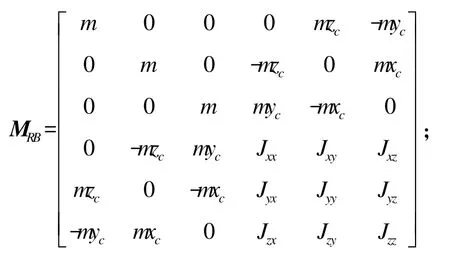
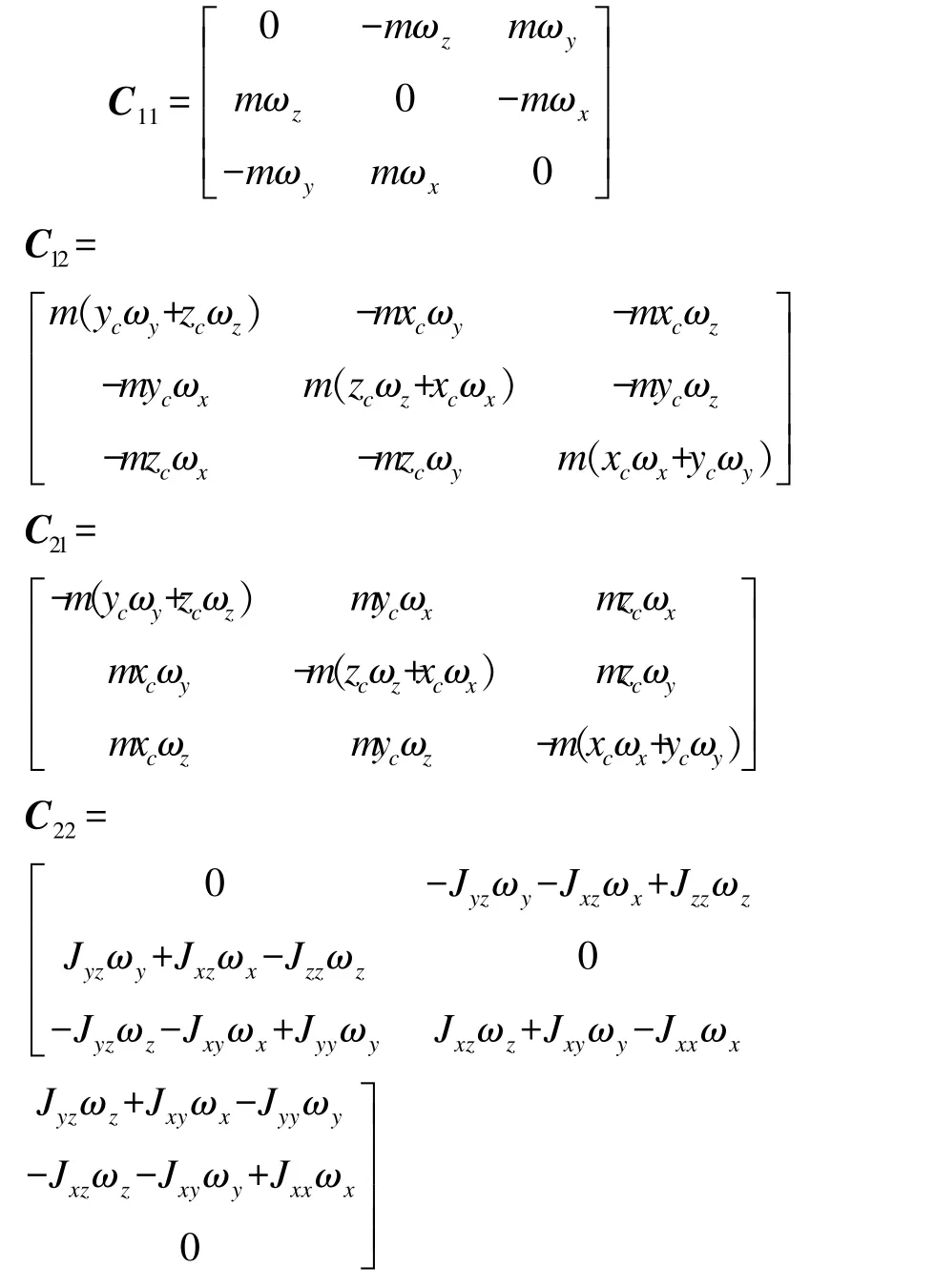
CRB(V)=为6×6阶矩阵,其各个子矩阵表达式如下:

针对水下平台座底过程中特殊运动工况,采用上述欧拉角方法描述平台运动姿态存在个别姿态角的不确定性。运动学方程可能出现奇异,例如当俯仰角为90°时,平台偏航角即为不确定状态。为此,引入哈密尔顿四元数描述平台旋转运动及空间姿态,避免参数退化,减少三角函数运算,提高计算精度[7,9]。

根据四元数定义及相关运算法则,可推导刚体平台角速度在体坐标系中的投影,用于表示刚体平台的旋转运动学方程:

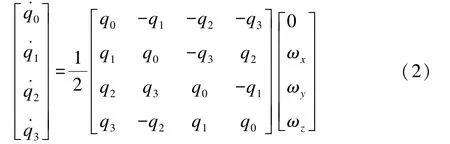
式中q0、q1、q2、q34个参数可描述平台转动,且存在如下联系方程:

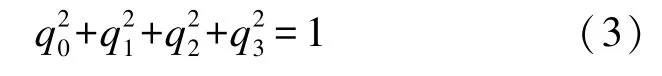
四元数替换空间欧拉角,可得到如下的地面系与体坐标系转换矩阵:

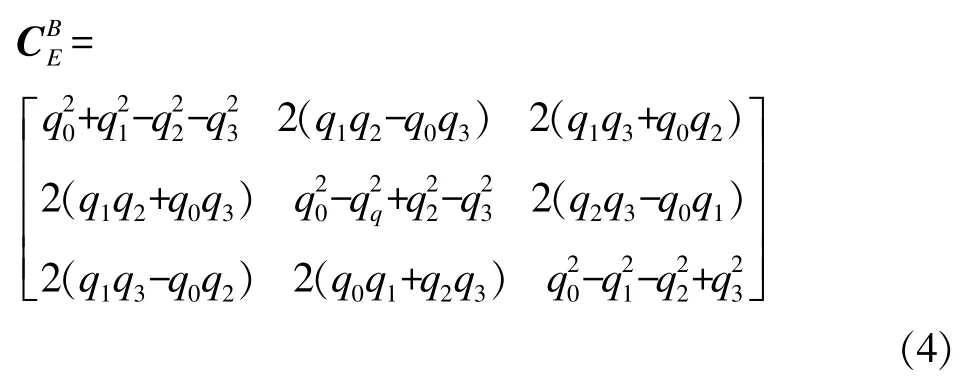
四元数与空间姿态角存在一定对应关系:

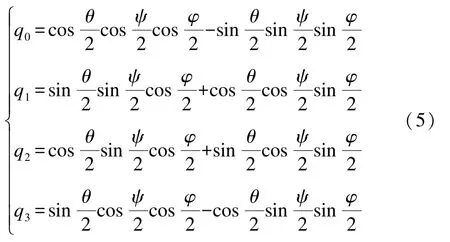
将式(5)分别代入式(2)、(4)中,即可得到通过哈密尔顿四元数建立的座底平台运动学方程。

3 平台座底过程受力分析

平台座底抗流底过程中所受到的作用力可大致分为以下几类:

1)系统体积力:包括其重力向量G=[0,-G,0]和浮力向量B=[0,B,0],由于体积力均指向铅垂方向故而一般将其合并为净浮力矢量ΔG,体坐标系下其表达式为

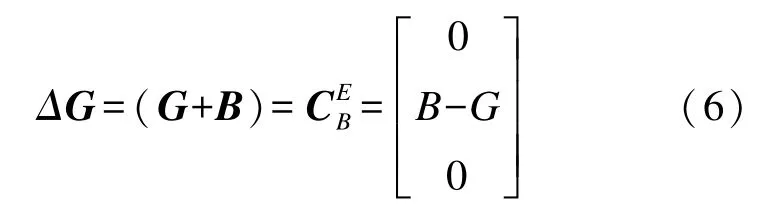
体坐标系下体积力对平台的作用力及力矩可表示为如下广义参数向量形式:

2)流体作用力:平台在流场中不可避免地会受到流体介质粘性的影响,诸多文献在这部分动力学研究中将粘性流体作用力分为3个部分[7]:定常直线平移运动引起的粘性位置力矢量Fμα、旋转运动产生的粘性阻尼力矢量Fμω、非定常运动引起的惯性力矢量Fλ。其中,粘性位置力向量计算方法如式(8)所示:

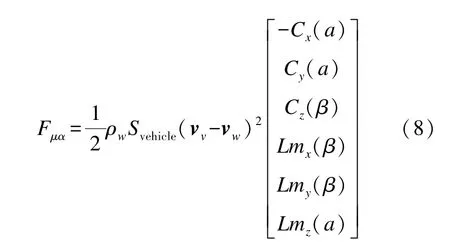
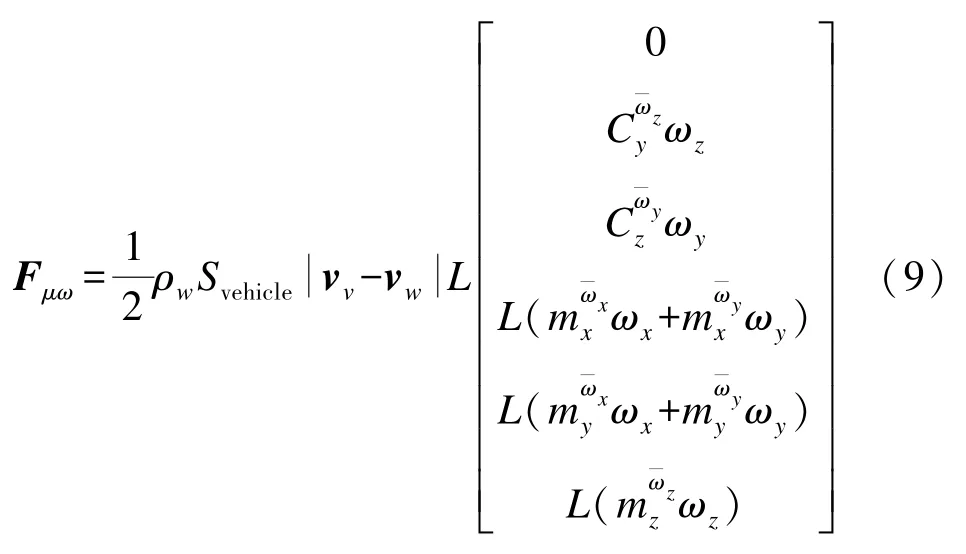
平台旋转运动造成的这部分流体动力增量,即粘性阻尼力矢量计算方法如式(9)所示:

平台在流体介质中的运动存在平移或旋转加速度时,势必会改变周围一部分流体的运动状态,这部分流体动力增量即为惯性力矢量,其具体表达方式如下:

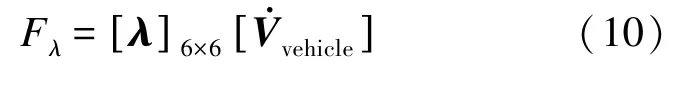
式中[λ]为附加质量矩阵,由平台空间6个自由度上总共36项运动惯性力组成。由曲面积分中使用的高斯散度定理(高斯-奥斯特罗格拉德斯基公式)可知,该矩阵关于主对角线对称,此外由于平台也近似为轴对称的刚体,[λ]可被简化为如下形式:

3)海底交互作用力:为获得平台与海洋底面之间的相互作用,首先要建立是否接触海底的判定条件,若满足以下2个条件中任意1个,则认为平台已经触底[10]:

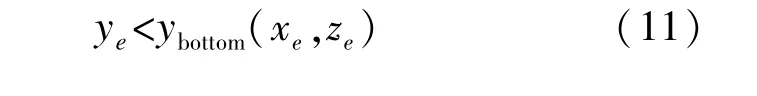
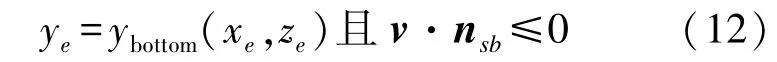
式中:xe、ye、ze为地面坐标系下平台底端面处轴向坐标;ybottom为海底三维连续曲面纵坐标;nsb为海底与平台底端面处接触位置的单位法向矢量,其方向始终由海底指向海水内部;v为平台速度矢量。

对于触底后的平台底端面,会受到海底平面法向支撑力矢量Fp及切向摩擦阻力矢量Fμ的作用。由弹性力学的基本理论可知:

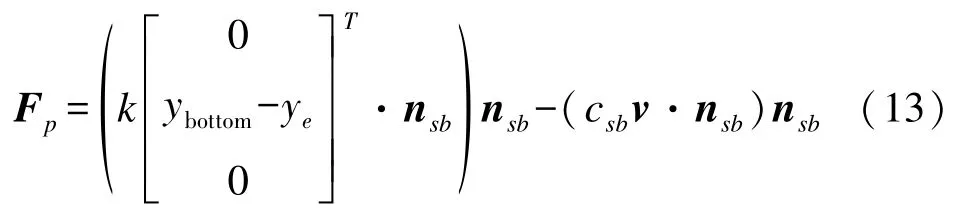
式中:k为与平台底面接触部分土壤的刚度;csb为海底粘性阻尼系数。一般在阻尼振动系统中,用阻尼比表达标准化的阻尼大小,此处,引入海底弹性支撑的阻尼比ζsb,其定义为

式中:mc为接触质量。将式(15)代入式(14)可以得到:

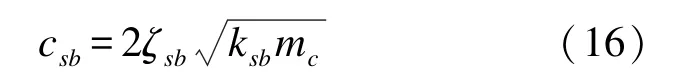
其中阻尼比ζsb定为0.5[11],可以在不显著影响系统整体响应的情况下消除碰撞海底引起的杂散高频扰动影响。

由结构力学的知识可知,刚度不仅仅与材料特性有关,还要考虑整体结构的影响,严格意义上讲,平台底端面接触部分海底平面刚度k与每个接触点上海底刚度ksb之间并不存在简单的线性转换关系,其取值只能通过大量海底试验测试的方法获取。然而对大多数系统而言,其总体运动响应对这一取值并不敏感,为简便起见,此处近似认为土壤与平台底面之间存在一系列相同的接触面单元并将其应力应变关系作为接触面的本构关系,每个接触面单元的刚度为

刚度k可以通过下式计算:

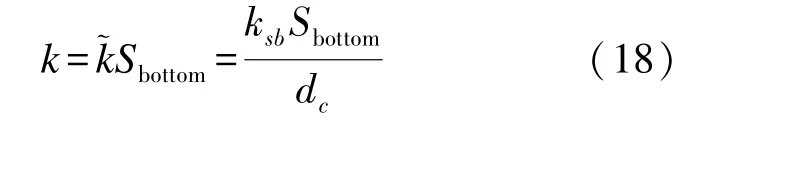
式中:ksb为海底刚度;Sbottom为平台底面与海底接触面积;dc为平台底面当量直径。

在满足海底接触条件的前提下,平台在海底三维平面切线方向上与海底存在相对运动的趋势或相对运动,使得两者之间存在摩擦阻力。计算摩擦阻力前,首先要得到速度矢量v在海底三维平面切向上的分量:

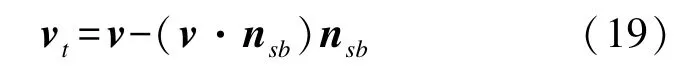
根据库仑摩擦定理,平台底面与海底两者之间存在动摩擦、静摩擦以及过渡状态3种情况:

①vt≠0时,潜标底面与海底在切向上存在相对速度,摩擦力矢量Fμ与摩擦面正压力成正比,方向与相对速度方向相反:

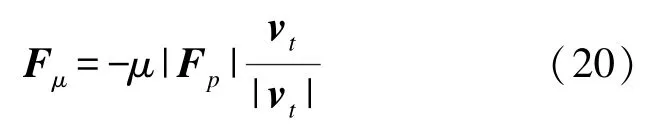
式中:μ为潜标底面与海底之间摩擦阻力系数且具有各向同性。

②vt=0且|Fμ|≤μ|Fp|时,潜标底面与海底之间在切向上仅存在运动趋势,属静摩擦力:

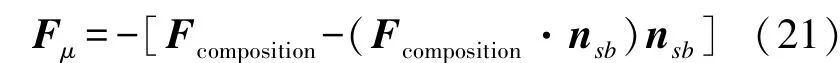
式中:Fcomposition=FBG+Fμa+Fμω+Fλ。

③vt=0且|Fμ|＞μ|Fp|时,此时处于过渡状态内,这是由于采用离散化模型进行数值求解造成的,此时摩擦力已经大于最大静摩擦力,但是潜标底面在海底平面切平面内仍无速度矢量。过渡状态是一个瞬时状态,只持续一个时间步长,在这个时间步长内完成静止状态到运动状态的转换,摩擦阻力Fμ为

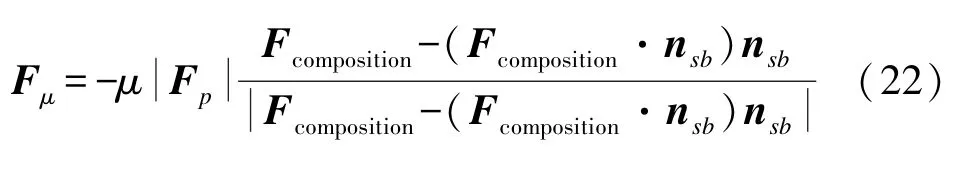
4 座底稳定性仿真计算

采用四阶龙哥库塔方法在时域范围内对系统坐底抗流运动学与动力学模型进行求解,部分计算输入参数如表1所示。

3 kn海流冲击作用下座底平台运动响应参数如图2-6所示。可以看到,系统在海流作用下发生偏转,俯仰角由90°开始振荡减小至88.7°附近,潜标偏转角约为1.3°;平台质心位置由于俯仰角的变动也发生振荡,稳定后y方向偏移2.3 mm,x方向偏移6 mm;质心位置的变动由于潜标偏转产生,海流作用下平台并未离地,其底端面始终与海底接触。

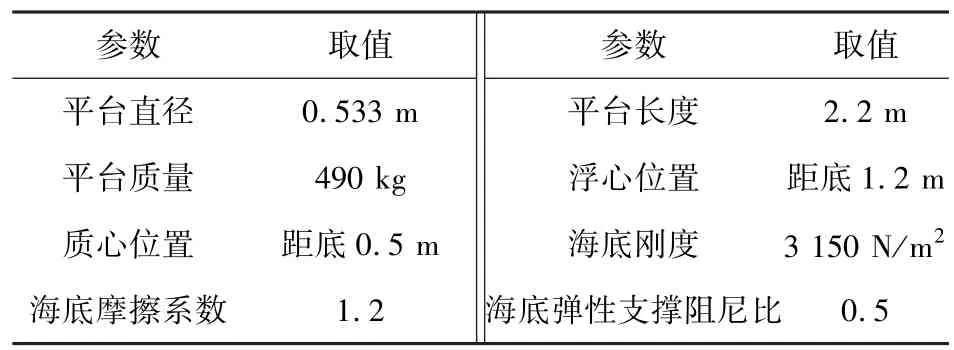
表1 稳定性分析计算输入参数表Table 1 Input parameters for stability analysis and calculation

由计算结果可知,该直立式水下无人座底平台可在3 kn流作用下保持稳定,具备抵抗3 kn海流能力。

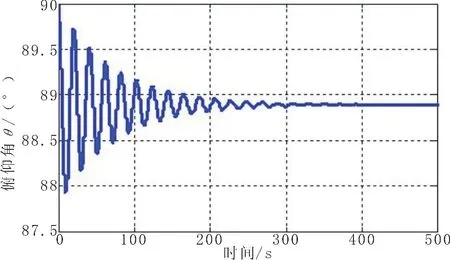
图2 座底平台俯仰角随时间变化情况Fig.2 Pitch angle of bottom-seated platform changing with time

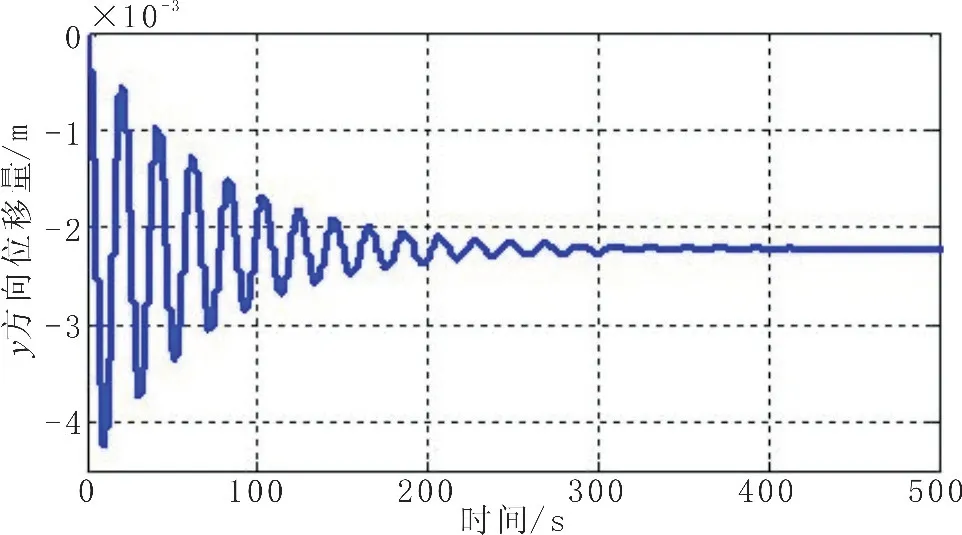
图3 座底平台质心竖直方向位移量随时间变化情况Fig.3 Displacement of bottom-seated platform's mass center in vertical direction changing with time

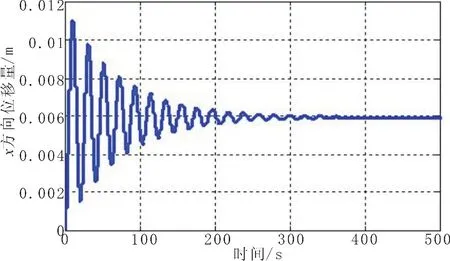
图4 座底平台质心水平方向位移量随时间变化情况Fig.4 Displacement of bottom-seated platform's mass center in horizontal direction changing with time

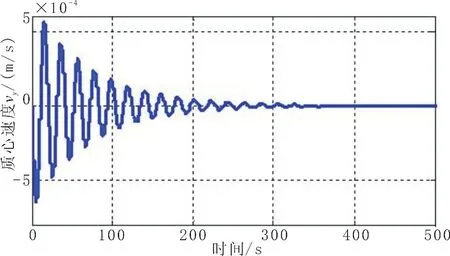
图5 座底平台质心竖直方向速度随时间变化情况Fig.5 Speed of bottom-seated platform's mass center in vertical direction changing with time

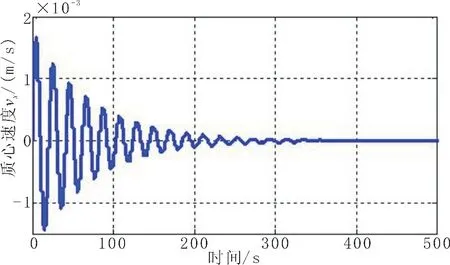
图6 座底平台质心竖直方向速度随时间变化情况Fig.6 Speed of bottom-seated platform's mass center in horizontal direction changing with time

5 结束语

本文在充分考虑海底土质真实物理特性的基础上,建立了海底的弹塑性数值模型,并基于刚体座底平台的动量与动量矩定力,结合四元数方法修正平台旋转与浮心运动方程,建立大攻角运动状态下座底平台三维空间运动数学模型,在此基础上对直立式水下平台座底后海流作用下的运动响应进行仿真预报,分析其抗流稳定性,可为后续设计工作开展提供有意义的参考。