基于舰船地震波的实时恒虚警概率时频检测

颜 冰,马剑飞

(海军工程大学 兵器工程系,湖北 武汉430033)

0 引言

海底可以看作是一个分层的粘弹性介质体,舰船低频振动传播至海底所激发的地震波[1-2]分为压缩波和切变波。压缩波即介质体积形变产生的纵波,它的传播方向与质点振动方向一致;切变波即介质剪切形变产生的横波,它的传播方向与质点振动方向互相垂直,一般统称压缩波和剪切波为体波。在特定的传播条件下,干涉相长的体波叠加出频率较低、能量较强的次声波,其能量主要集中于分界面附近,离开分界面一个波长的距离后将迅速衰减,因此称之为界面波。界面波具有频率低、传播速度低、扩展损失小于体波等特征[3-4],若在分界面上布放与海底介质充分耦合的地震波检测系统,能够有效地接收到舰船地震波产生的界面波信号,后文所提及的舰船地震波信号均指地震波的界面波信号。

1 恒虚警概率线谱检测原理

在自然环境下,地震波传感器接收的背景噪声信号中一般不会包含明显的线谱成分,而航行舰船由于螺旋桨、内燃机等周期性运动部件的存在,其辐射噪声中会含有较强的稳定线谱分量[5]。因此可把对舰船目标的检测简化为高斯背景噪声下的单频线谱检测,式(1)是建立的二元假设检验模型:

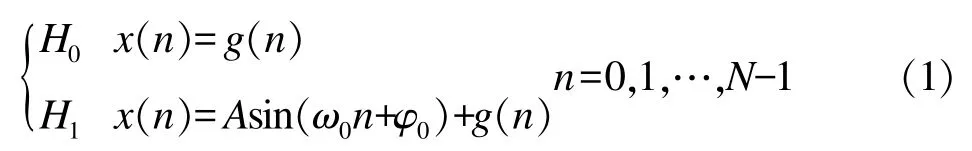
式中:H0设为测量信号中无目标信号成分;H1设为测量信号中存在目标信号成分;ω0=2πf0/fs为归一化角频率,f0表示目标信号频率,fs为信号采样率;φ为初始相位;噪声g(n)是方差为的加性高斯噪声即g(n)～N(0,)。

对x(n)进行DFT变换可得到[6]:

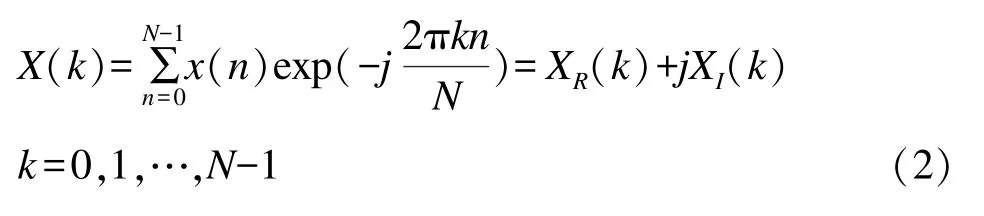
其中,

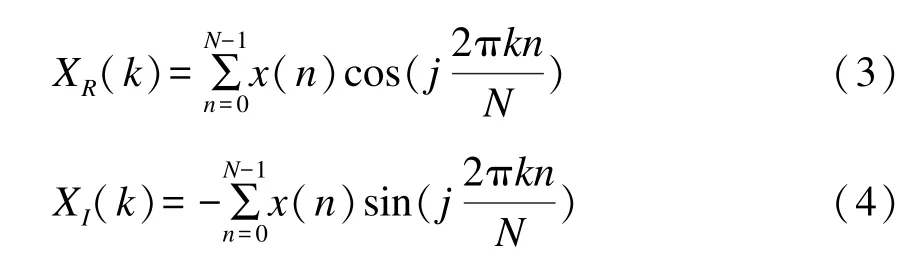
XR(k)和XI(k)分别满足高斯分布:

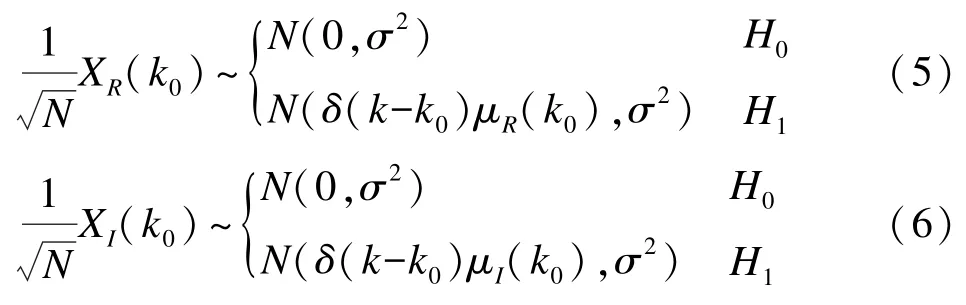
式中:δ为单位冲激函数;的值与采样点数、信号频率和采样频率都有关,此处φ0仅作为一个过程变量不加以求解。

定义功率谱检测器为

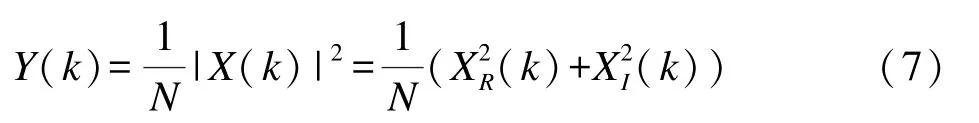
文献[7]已经证明了XR(k)与XI(k)相互独立。结合式(5)-(7)可知,在H0假设条件下,XR(k)与XI(k)均服从均值为0的高斯分布,所以x(n)的功率谱Y(k)服从自由度为2的标准卡方分布;在H1假设条件下,当k≠k0时,x(n)的功率谱Y(k)仍服从自由度为2的标准卡方分布;当k=k0时,x(n)的功率谱Y(k0)服从自由度为2的非中心卡方分布。因此Y(k)服从的卡方分布可表示为

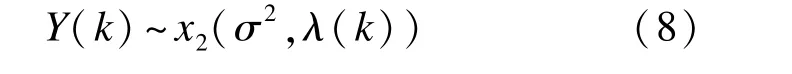
式中:λ(k)参数的取值定义为XR(k)与XI(k)所服从的正态分布的均值平方和,即

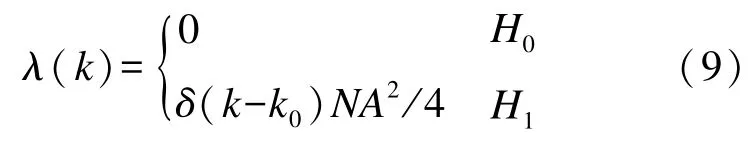
相应地,两种假设条件下信号功率谱的概率密度函数为

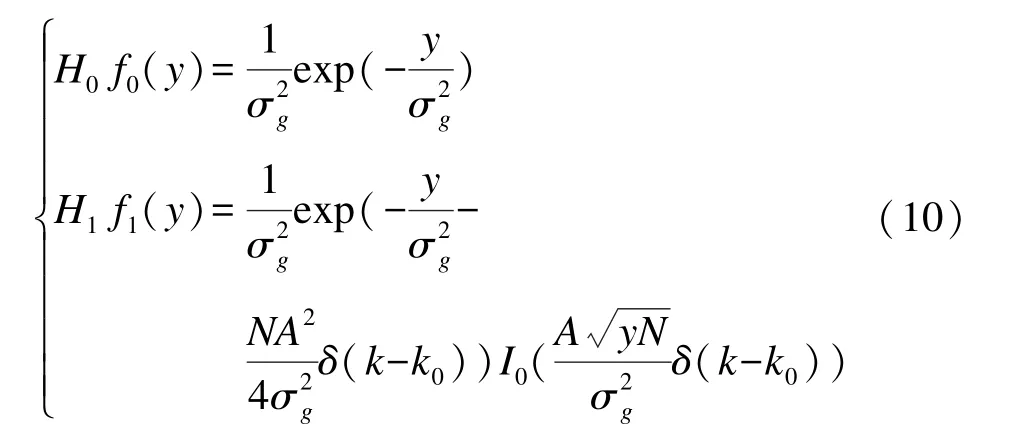
式中:f0(y)为无目标时的信号功率谱概率密度函数;f1(y)为有目标时的信号功率谱概率密度函数;I0为第一类修正零阶贝塞尔函数。

当信号时间带宽足够大时,可认为经过DFT变换后各谱线的系数是独立的[5],因此由二项分布的计算公式可得虚警概率PFA为

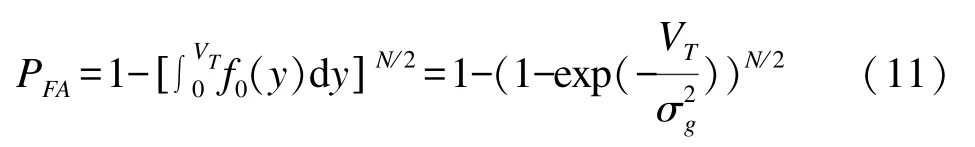
式中:VT为检测门限。求解上式可知,当虚警概率PFA设定时,对应的检测门限VT为

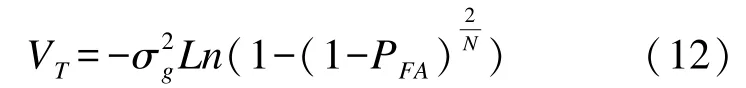
由二项分布的计算公式可得恒虚警概率检测的检测概率PD为

图1(a)-(d)分别是数据长度l为256点、512点、1 024点和2 048点时,在0.1%、1%和10%虚警概率下信噪比与检测概率的关系。信噪比定义为

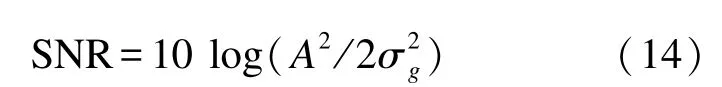
通过对比可以看出,在一定的虚警概率下随着数据点数的增加,检测概率有明显的提升,但在检测过程中如果窗函数截取的数据段过长则会导致时间分辨率变差。

图1 不同信号长度下的检测概率Fig.1 Detection probability at different signal lengths

2 实时恒虚警概率时频检测

2.1 实时恒虚警概率时频检测原理

在对恒虚警概率线谱检测算法性能充分地分析之后,下面提出一种实时恒虚警概率时频检测算法。

由图1(d)可知,当信噪比大于-17 dB时,三种虚警概率情况下的检测概率超过90%。在综合考虑时间分辨率、频率分辨率和低信噪比检测的因素后,恒虚警概率时频检测的窗函数选取为长度2 048点(时长4.5 s)、重叠率50%的矩形窗,对应的频率分辨率为0.22 Hz。

利用长度为N(N=2 048)的矩形窗截取时域信号,每次更新数据点数为1 024(时长约为2.25 s)。对窗函数截取的第i次信号xi求功率谱(直接法)使时域信号变换到频域上:

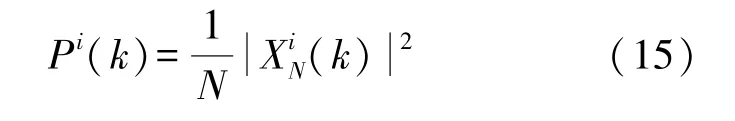
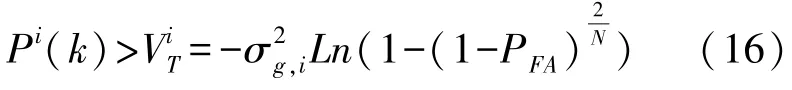
使

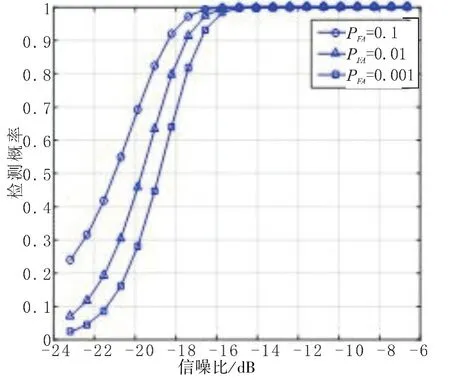
图2 低信噪比检测概率Fig.2 Detection probability at low SNR

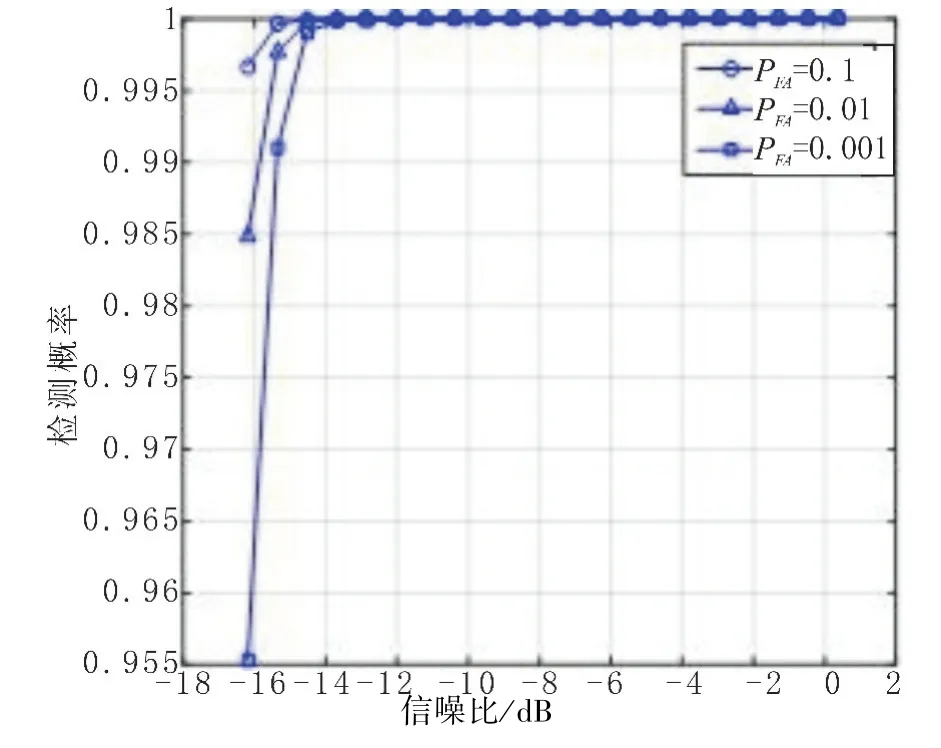
图3 高信噪比检测概率Fig.3 Detection probability at high SNR

2.2 实时恒虚警概率时频检测结果分析

直接利用该算法对实测信号进行检测,发现谱线十分杂乱,不利于对目标的检测决策。分析其主要原因是在恒虚警概率检测推导过程中将舰船目标的检测简化为含噪声信号的单频线谱检测,实际舰船地震波信号不是一个简单的单频信号,而是由多个有一定带宽的窄带信号混合而成,而且背景噪声不是完全的高斯噪声,在某些时间段内存在有色干扰噪声。

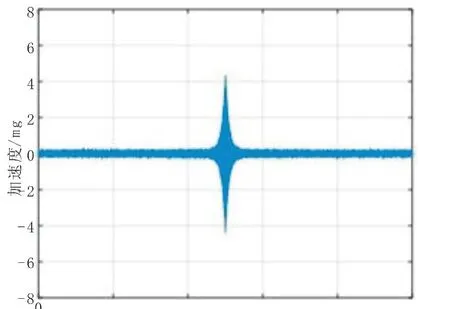
图4 仿真信号Fig.4 Simulation signal

为进一步识别舰船目标的谱线,假定舰船目标的信号为当前时间段内的最强谱线,此时对谱线的检测转化为求出过检测门限的最强谱线。

1)仿真信号检测结果分析。

以单频简谐波的形式近似分析舰船地震波加速度信号在Kelvin黏弹性介质的传播过程[8],与均值为0、方差为0.004 9的高斯白噪声相加后,得到的仿真信号时域波形仿真信号如图4所示。

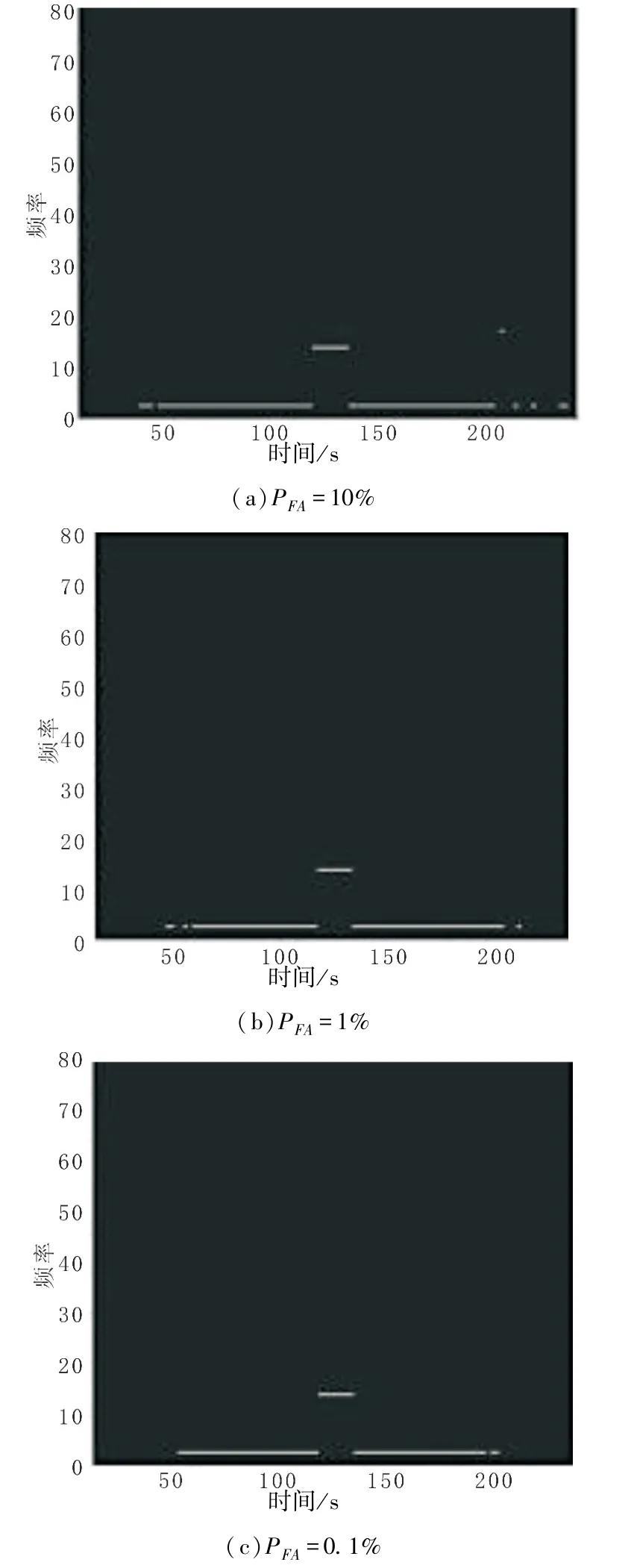
图5 仿真信号检测结果Fig.5 Test results of simulation signal

图5(a)-(c)是在不同的虚警概率下,恒虚警概率时频检测算法对于仿真信号的检测结论(检测结果为1用亮点标出,检测结果为0用暗点标出,横坐标为时间,纵坐标为频率)。可以看出预警时长与虚警概率正相关,3种情况下的预警时长都超过了75 s(预警时长定义为时域峰值时刻与单频点处开始出现连续谱线时刻的差值)。以第50 s时刻为例,此时的信噪比低至-18.02 dB仍可检测到目标。对目标检测的预警时长随虚警概率而增加,但虚警概率太高也会导致检测的谱线结构变得杂乱,从而不利于对目标进行检测决策。

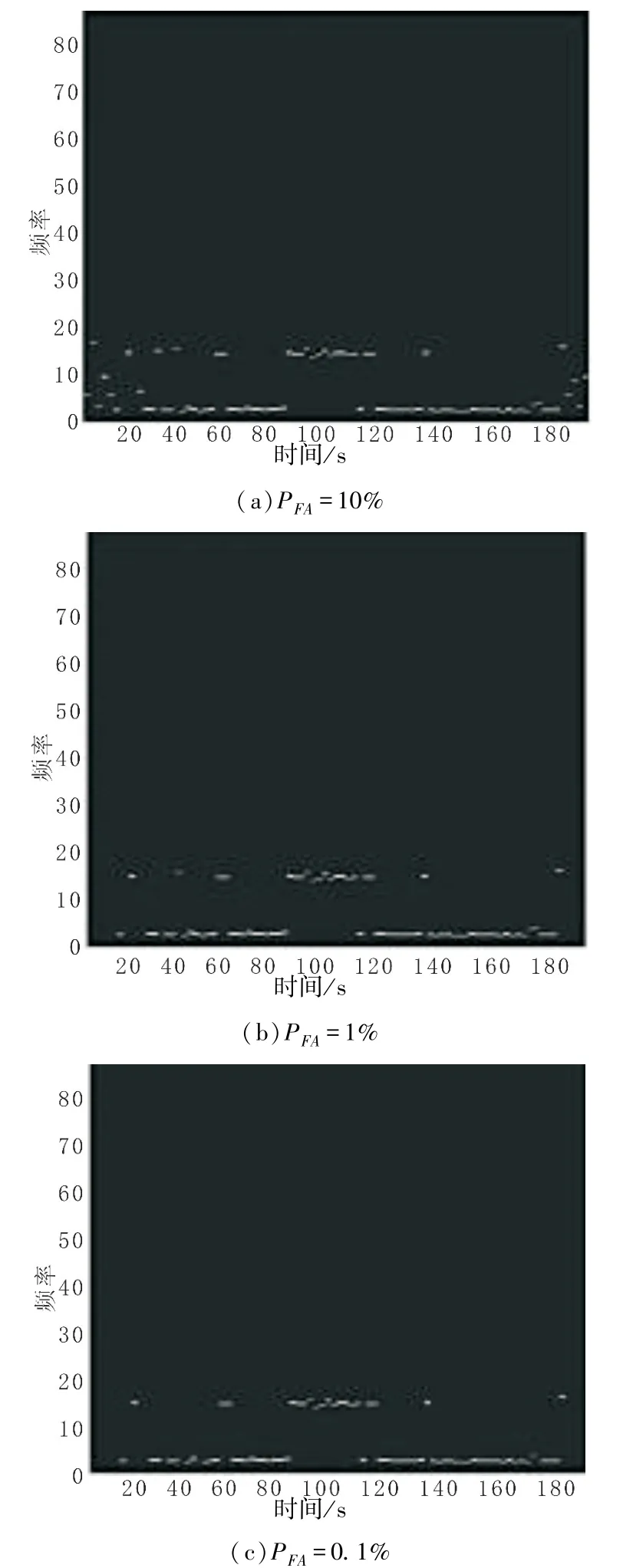
图6 实测信号检测结果Fig.6 Test results of measurement signal

2)实测信号检测结果分析。

图6(a)-(c)是在不同的虚警概率下,恒虚警概率时频检测算法对于仿真信号的检测结论。对目标的预警时长随虚警概率而增加,以1%的虚警概率的检测为例,此时预警时长达到70 s,换算成检测距离为350 m。

2.3 实时时频检测决策算法及结果分析

前述的预警时长仅是通过观测的方式得到,下面设计一个简易的检测决策算法。基于对过门限最强谱线检测结果的二值化,建立探测系统对舰船地震波加速度信号的判别准则:

1)预警准则。若连续的5个时刻在同一频点附近出现过门限最强谱线的点数大于3个,即满足式(18)时,则使系统处于预警状态:

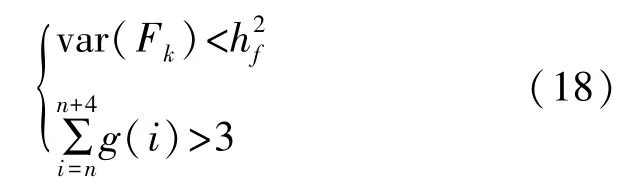
并且记

式中:Fk=[fk(n),fk(n+1),fk(n+2),fk(n+3),fk(n+4)]是连续5个时刻过门限最强谱线对应的频点组成的向量,若某个时刻无过门限谱线,则在Fk中缺省此时刻对应的fk;g(i)为i时刻的判别结果,若i时刻出现过门限谱线则g(i)=1,相反地令g(i)=0;hf为描述谱线在当前时间段的波动范围门限值,本测试过程中,hf取值为5。当整个预警判别完成后,令n=n+5,继续新一轮的判别。

2)放弃预警准则。当系统处于预警状态后,若连续三轮的式(18)判别都不成立时,则系统恢复初始状态。

3)确认目标准则。当系统处于预警状态后,记新出现的过门限谱最强谱线频点的均值为μk+1。若式(20)成立,则输出确认目标信号。

利用设计的决策算法在3种虚警概率下对实测舰船地震波信号和仿真信号进行检测,结果如表1和表2所示。表中,预警时刻为开始处于预警状态的时刻,确认时刻为确认舰船目标的时刻,重新定义预警时长为峰值时刻与预警时刻的差值。

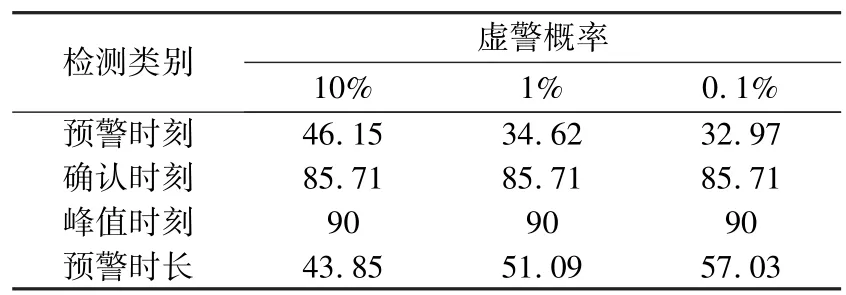
表1 实测信号检测结果Table 1 Detection result of measurement signal

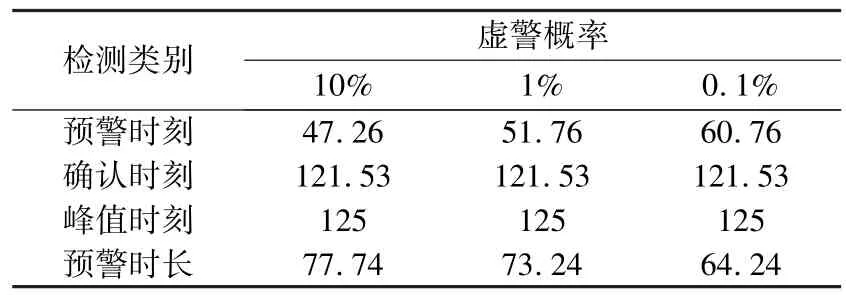
表2 仿真信号检测结果Table 2 Detection result of simulation signal

可以看出,仿真信号的预警时长是随虚警概率的上升而增加,这与理论是相符合的。但对于实测信号而言,其在10%虚警概率下的探测时长小于1%和0.1%虚警概率下的探测时长,这主要是由于实测信号的频谱较为复杂而决策算法又对谱线的分布进行了严格的限制,因此在设计系统时要充分考虑虚警概率与检测距离的关系。

3 结束语

本章在恒虚警概率线谱检测算法的基础之上,提出了实时恒虚警概率时频检测算法,并从仿真信号和实测信号2个方面检验了该算法的有效性。该算法克服了传统时域包络检测舰船目标的局限性,既提升了探测的距离又提高了探测的可靠性。其门限值与虚警概率成反比且随噪声而动态变化,所以算法具有自适应性及不依赖于设计者的经验值的优势。另外,此算法是基于工程应用的角度提出的,运算复杂度低,该检测算法仅要求系统可在2.2 s之内运算一次2 048点的FFF变化即可,其它的运算过程都只是简单的方差计算和大小判别。以STM32系列单片机为例,其DSP库中的FFT变换函数执行2 048点FFT运算的耗时仅在毫秒级别,所以此算法以单片机作为载体可实时地进行检测运算;最后设计了识别目标的决策算法,能够计算出预警时刻与确认时刻,为水下预置武器的使用提供依据。