从Lebesgue测度看R2中图形的面积∗

余玉峰 石冶郝 孙 颖

(1.山西师范大学现代文理学院,山西 临汾 041000;2.首都师范大学初等教育学院,北京 100048;3.湖南省邵阳市大祥区祥凤实验学校,湖南 邵阳 422000)

0 引 言

面积是数学的基本研究对象.在初等数学中学生从直观上感受了一些常见的规则图形的面积,如三角形,平行四边形,梯形[1,第6章,85～104页]及圆[2,第5章,57～78页]等.

到了高等数学,学生需要计算不规则图形的面积.在数学分析中采用Riemann定积分的方法给出一些特殊图形面积的定义.但这种方法仍有局限性,后来又提出了可求面积的定义.这就极大地推广了面积的定义,使很多不规则的图形都具有了确定的面积.但问题又出现了,一些不太特殊的不规则几何图形仍然没有面积的定义,例如

问题1如果设A为[0,1]×[0,1]中的有理点构成的集合,B为[0,1]×[0,1]中的无理点构成的集合,那么A和B有没有面积呢?如果有,是多少?

类似的集合还有很多,例如可数集等.要解决这些问题,用可求面积的定义及Riemann定积分的定义已经不够了.因此,这迫使人们不得不重新思考面积.于是,在实变函数中采用更广泛的Lebesgue测度来代替面积的定义.从而一些复杂的几何图形都可以计算“面积”,问题1就迎刃而解.

本文的目的是使读者对R2中图形的面积有一个深入的认识,要说明的结论是Lebesgue测度是目前“面积”定义最大的推广.本文的安排遵循由特殊到一般,由简单到复杂的思路.首先,回顾R2中规则图形的面积,这要追溯到正方形面积.其次,介绍R2中一些不规则图形面积的定义及计算方法.最后介绍R2中一般图形面积的推广——Lebesgue测度,并指出R2中的一些Lebesgue可测集类的测度与“面积”的关系.

1 R2中图形的面积

1.1 R2中规则图形的面积

正方形的面积等于其边长的平方(参见[1,87～89页),这个公式不是证明出来的,而是一种约定.有了这个约定,就可以得到R2中很多规则图形的面积.例如长方形的面积由正方形的面积推出;平行四边形的面积由长方形的面积推出;梯形的面积由平行四边形的面积推出;三角形的面积由平行四边形的面积推出.多边形的面积由三角形的面积推出;以及由长方形、平行四边形、梯形、三角形经过有限次组合而得到的图形的面积都可以计算出来.

如果把极限的思想运用到图形面积的定义中,就可以得到圆面积的计算公式,见割圆术([3,191页;4]).由圆面积可得扇形面积的计算公式.

最后由长方形(正方形)、平行四边形、梯形、三角形、圆和扇形经过有限次组合而得到的图形的面积都可以计算出来.这些规则图形或规则图形的有限次组合而得的图形面积是确定的,也能计算出来,主要原因是R2中正方形面积的约定.

1.2 R2中不规则图形的面积

下面,考察 R2中不规则图形的面积.首先研究几个特殊的不规则图形的面积.如图1,连续曲线y=f(x)≥0 在[a,b]上形成的曲边梯形的面积这里的积分是Riemann 定积分,也就是说曲边梯形的面积是通过Riemann 定积分定义的,即通过分割、近似代替、求和、取极限四步得到.类似的,如图2,由上下两条连续曲线y=f1(x)与y=f2(x)(f1(x)≤f2(x),a≤x≤b)以及两直线x=a与x=b所围成的图形面积为

图1

图2

对于一般不规则图形的面积,先给出可求面积的定义[6,223页].设P是一平面有界图形,用某一平行于坐标轴的一组直线网T分割这个图形.这时,直线网T的网眼 ——小闭矩形Δi可分为三类：

(i)Δi上的点都是P的内点;

(ii)Δi上的点都是P的外点,即Δi∩=φ;

(iii)Δi上含有P的边界点.

将第(i)类小矩形的面积加起来,记这个和数为sP(T);将第(ii)类和第(iii)类小矩形的面积加起来,记这个和数为SP(T).令

图3

图4

根据可求面积的定义,可以证明上述两类不规则图形是可求面积的.此外,单连通区域和多连通区域都是可求面积的,见图3、图4中的区域D.

这样,很多不规则图形的面积就有了准确定义.并非平面中所有的点集都是可求面积的,如问题1 中的图形A,见如下命题.

命题 1.1问题 1 中的图形A是不可求面积的.

证明：首先,图形A无内点.所以A被平行于坐标轴的一组直线网T分割以后(见图5),直线网T的网眼只有第(ii)类和第(iii)类小闭矩形Δi.所以第(i)类小矩形的面积和为零,即sA(T)=0.因此A的内面积

容易看出正方形[0,1]×[0,1]内和边界上的小矩形都含有A的边界点,[0,1]×[0,1]外(不包括边界)的小矩形内的点全是A的外点.由此可得A的外面积为

图5

若使问题 1 中的图形A具有面积,“面积”定义还需要进一步推广,这个推广就是下面的 Lebesgue 测度.

2 R2中的Lebesgue测度

事实上,经常使用的面积应满足类似于长度公理(见[7,53页])的面积公理.

公理(面积公理)设R2中的一些点集所构成的集合族μ,对于每个E∈μ,都对应一个实数m,使得

(1)(非负性)m(E)≥0;

(2)(有限可加性)如果E1,E2,…,En两两不相交,那么

(3)(正则性)m([0,1]×[0,1])=1.

因此要解决问题1,必须要修改面积公理.面积公理中的(1)和(3)是不能修改的,因为修改后与习惯不符.因此只有修改(2).将(2)的有限可加性改为可列可加性,就得到如下的 Lebesgue 测度公理.

公理2.2([7,54页],Lebesgue 测度公理)设R2中的一些点集所构成的集合族μ,对于每个E∈μ,都对应一个实数m,使得

(1)(非负性)m(E)≥0;

(2)(可列可加性)如果E1,E2,…,En…两两不相交,那么

(3)(正则性)m([a,b]×[a,b])=(b -a)2.

注：可列可加性包含有限可加性的情况,只要令m(φ)=0 即可.

下面在Rn中寻找一集合类μ,在μ上满足 Lebesgue 测度公理.因为在Lebesgue 测度公理中出现了集合的可数并运算,所以μ对集合的可数并运算是封闭的.自然地,要求μ对集合的作交及作差运算也是封闭的.而满足卡拉泰奥多里条件的Lebesgue 外测度正好能满足这一要求.下面来看 Lebesgue 外测度(见[7,56页;8,10页])的定义.

设E为R2中任一点集,对于每一列覆盖E的开区间(某些Ii可以是空集),作出它的体积总和(μ可以等于 + ∞ ,不同的区间列一般有不同的μ).所有这一切的μ组成一个下方有界的数集,它的下确界(完全由E确定)称为点集E的 Lebesgue 外测度,简称 L 外测度或外测度,记为m∗E,即

设E为 R2中的点集,并且对任一点集T都有

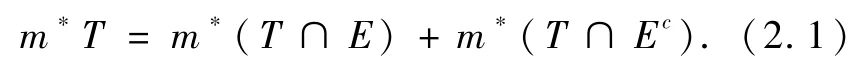
等式(2.1)称为卡拉泰奥多里条件([7,62页;9,127页]).

记μ为R2中所有满足(2.1)的点集E构成的集合,m为满足(2.1)的外测度m∗,则m和μ满足一系列性质,例如μ对集合的可数并、作交及作差运算是封闭的,m在μ上满足可数可加性等.因此μ和m就是要找的集合类及满足 Lebesgue 测度公理的新的“面积”.此时,称μ中的集合E是 Lebesgue 可测集,简称 L 可测集或可测集,E的外测度m∗E称为E的 Lebesgue 测度,简称 L 测度或测度,记作mE([7,62页]).最后记 Lebesgue 可测集构成的集合为μ.

Lebesgue 测度除了以上的定义法,还有一种内填外包的定义法(这时要引入内测度),见[10,38～42页]中第2.3 节,但这两种定义是等价的,见[7,324页].

3 R2中Lebesgue测度与面积的关系

在这一节,我们将说明 Lebesgue 测度与以前面积相比的优越性,以及它们之间的关系.

3.1 规则图形

我们先来看Rn中区间的定义.Rn中集合的直积分别称为开区间,闭区间,半开半闭区间,它们都称为区间.称为区间I的体积.易知在R2中区间是矩形区域,区间的体积就是矩形区域的面积.

R2中的所有矩形区域都是可测集,且它们的面积等于它们的测度,见[7,67页]中定理2.

推论3.1R2中的平行四边形区域是可测集,且它们的面积等于它们的测度.

图6

证明：如图6.设G表示平行四边形ABCD所在的区域,表示G的闭包,表示G的内部,则和都是可测集.过点B作BE垂直于CD交CD于E,过点A作AF垂直于CD交CD的延长线于F.将ΔBCE平移到ΔADF,则四边形ABEF是矩形.设H表示矩形ABEF所在的区域,则和都是可测的,且它们的测度都等于矩形ABEF的面积,又等于平行四边形ABCD的面积即G的面积.

类似可得R2中的其它规则图形(如平行四边形、梯形等)以及由这些规则图形经过可数次组合而得到的图形区域都是可测集,而且它们的面积等于它们的测度.

3.2 可求面积的图形

R2中可求面积的图形区域也是可测集,见如下定理.

定理3.2在R2中可求面积的图形是可测集,而且它的测度等于它的面积.

证明定理3.2 之前,我们先给出一个引理.

引理3.3在R2中面积为零的图形是可测集,而且它的测度等于零.

证明：设P是 R2中面积为零的图形,用平行于坐标轴的一组直线网T分割P.直线网T的网眼——小闭矩形Δi可分为三类(见本文1.2 节中可求面积的定义).记第(i)类小矩形的面积和为sP(T),第(ii)类和第(iii)类小矩形的面积和为SP(T),且为P的外面积.由于P是可求面积且面积为零,所以

记第(ii)类和第(iii)类闭矩形为Δi,i =1,2,….对任意ε ＞0 总存在开区间Ii,使得

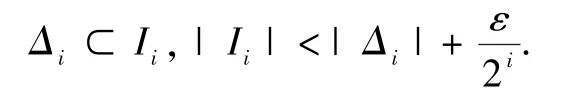
由ε ＞0 的任意性及m∗(P)的定义得

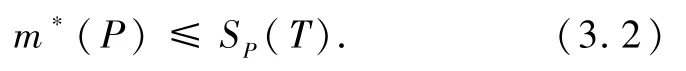
所以由(3.1)和(3.2)可得：m∗(P)≤=0.从而P是可测集,且它的测度等于零.

定理3.2 的证明：将(1.1)式中的P换为或P∂P(为P的闭包,∂P为P的边界)后,我们可得

因此若P是可求面积的,则和P∂P也是可求面积的.由P是可求面积的知P的边界的面积为零(见[6,224页]的定理21.2).由引理 3.3得

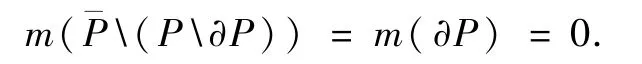
(i)设直线网T分割P时,第(ii)类和第(iii)类闭矩形为Δi,i =1,2,….对任意ε ＞0 总存在开区间Ii,使得从而

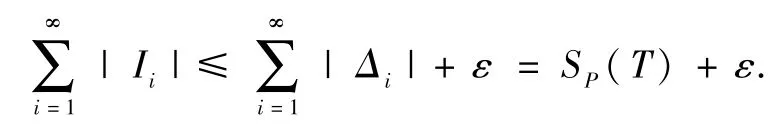
由ε ＞0 的任意性及m∗(P)的定义知

所以

(ii)设直线网T分割P时,第(i)类闭矩形为Δi,i =1,2,…;Ii为覆盖P的任一列开区间,则

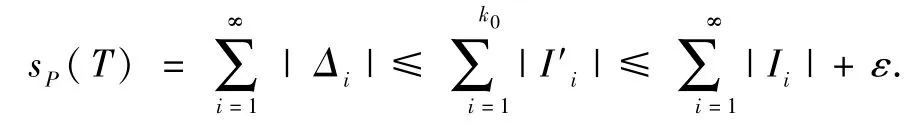
因此

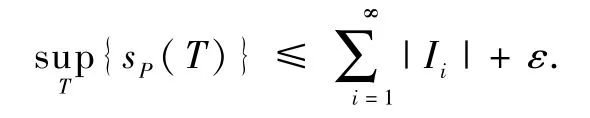
进而

是 R2中覆盖 P 的任一开区间列} + ε,即

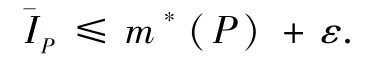
由ε ＞0 的任意性得,

注：在R2中,可求面积的图形是可测集,但可测集(图形)不一定是可求面积的,见命题1.1.

3.3 其他图形

从以上讨论可知R2中的规则图形及由规则图形经过可数次组合所得的图形,可求面积的图形都是 Lebesgue 可测集,并且它们的“面积”就等于它们的Lebesgue 测度.Lebesgue 测度的定义极大地推广了 “面积” 定义,使简单的和很多复杂的几何图形面积都有了准确定义,例如有限集,可数集,开集,闭集,Gδ型集,Fσ型集等(见[7,第3章第3节,67～71页]).尽管 Lebesgue 不可测集(见[7,第3章第4 节,71～74页])仍然存在,但 Lebesgue测度是目前 “面积” 最大的推广.

对于高维空间中的低维测度目前还处于研究中,因此高维空间中的“面积”缺乏像 Lebesgue 测度一样广泛的定义.另外,面积除了 Lebesgue 测度外还有其它的测度,见[11,第7.7 节,336～350页]和[9,第3章第10 节,125～148页].

3.4 问题1的解

由可测集的定义知单点集的测度为零,从而由可测集的可数可加性得有限集和可数集的测度为零(见[7,64页]).由于在问题 1 中,集合A是可数集,因此m(A)=0.从而由测度的有限可加性知m(B)=m([0,1]×[0,1])- m(A)=1-0=1.这样用测度代替面积以后,轻松解决了问题1.