大直径不锈钢棒料剥皮机刀盘结构设计及模态分析
2019-05-07屈银虎成小乐祁志旭刘晓妮周思君
梅 超,屈银虎,成小乐,祁志旭,刘晓妮,周思君
(西安工程大学 材料工程学院,陕西 西安 710048)
0 引 言
随着现代制造业的发展,不锈钢棒料在工业领域得到了广泛的应用。为保证产品的质量,工业上一般采用剥皮机对棒料进行表面处理,得到尺寸和精度均符合要求的棒料[1]。其中,刀盘系统作为大型剥皮机关键技术研究的核心,其主要作用是在旋转的过程中实现刀具对棒料的切削,它的结构形式直接影响切削加工的效率和切削棒料的精度。因此,在刀盘系统的设计中要保证刀具调整时使其运动保持高度的同步性。剥皮机刀盘上安装多把刀具,经过一次对刀后可完成同一批次棒料的车削,大大提高了切削效率和被加工件的表面质量精度。为此,设计合理的刀盘系统是配合主轴传动系统的需要,也是保证剥皮机工作性能和加工精度的必要前提[2]。
文献[3]提出了一种用于棒料加工的剥皮装置,主要结构是主轴带动剥皮机刀盘旋转,刀盘上布置4个刀架,对棒料进行切削,但没有具体说明其运动原理;LING等[4]建立了刀盘系统动力学模型,并基于振动响应结果对疲劳寿命进行了预测。张亮等[5]对刀盘进行有限元分析,分析应力-应变的变化规律,证明了设计结构的合理性;刘志杰等[6]运用组合修改实例的方法对刀盘进行设计,总结设计计算的方法。但目前,对于刀盘模态分析的研究相对较少;张红星等[7]从受力结构的刚度及刀盘结构形式方面浅谈了刀盘振动问题,提出选型和设计方面的建议;敖日汗等[8]分析了刀盘底座半径、柔度与振动的关系,解决了振动问题;吴玉厚等[9]提出刀盘系统第一阶振动频率远远大于实际工作中的频率;张建水等[10]利用ANSYS对刀盘系统进行模态分析,得出刀盘各部分振动的强弱分布及抗振薄弱区,并以此为依据对刀盘进行优化,以提高刀盘在工作过程中的抗振性能。基于前人的研究基础,本文对剥皮机在多刀同时工作这一复杂工况下进行研究,对刀盘系统进行建模,并进行自由模态分析,根据最大振幅出现位置区域,提出刀盘结构优化方案,并进行对比分析验证。同时,对刀盘系统进行静力学分析,计算刀盘系统最大的应力、应变是否满足剥皮机的工作需求,实现满足工作需求强度与自动调刀精确的刀盘系统。
1 建模及模态分析
1.1几何模型的建立
剥皮机切削金属棒料时,刀盘按顺时针方向旋转,根据切削棒料所产生的主切削力的方向,将刀盘设计为薄壁构件,在安装零部件的位置设置较大的壁厚,并减薄刀盘中心厚度,以减小刀盘质量,更有利于刀盘旋转;对刀盘上固定刀架一侧进行加厚,以满足其强度需求。利用Solidworks建立原始刀盘结构模型,如图1所示,刀盘直径为480 mm并通过螺钉固定在主轴齿轮上,随主轴齿轮一起旋转。
1.2结构模态分析
为确保刀盘结构具有良好的动态性能,需要对刀盘结构进行动态设计,而结构模态分析是结构动态设计的核心部分。因此,模态分析可以有效避免刀盘结构的固有频率和刀架的频率产生共振,导致机构失效,从而影响产品的加工精度。另外,通过模态分析可以确定刀盘各阶固有频率和振型,也为制订施工方案以及改进刀盘结构提供参考。
1.2.1 模态分析过程 刀盘结构模态与结构形式、材料参数等有关,与外载荷无关。当外界激励频率接近于结构固有频率时,结构会发生共振,影响结构安全[11]。本文运用ANSYS Workbench软件对刀盘结构进行模态分析[12-14]。将模型导入ANSYS Workbench,材料HT250的弹性模量为1.5×1011Pa,密度为6 900 kg/m3,泊松比为0.25,划分网格,选择单元类型[15]。因本文主要分析刀盘自由模态,故不对刀盘施加固定约束处理。
在对刀盘进行网格划分时,考虑到刀盘结构、计算精度和时间等因素,且刀盘模型比较复杂,划分六面体网格较困难,因而,采用Ansys workbench中的Tetrahedron(四面体)以及人工控制网格密度完成网格划分。其中,单元的尺寸长度为10 mm,最终划分的单元格数为94 346,节点个数为150 139,刀盘有限元模型如图2所示。

图 2刀盘的有限元模型Fig.2 Finite element model of the cutter
1.2.2 模态分析结果 对刀盘进行模态分析后得知刀盘的前6阶模态为刚体模态,固有频率接近于零,因此分析刀盘的固有频率和模态振型从第7阶开始。对刀盘而言,低阶模态在切削过程中起主导作用,故本文提取了刀盘自由模态分析结果的前10阶数据,如表1所示。
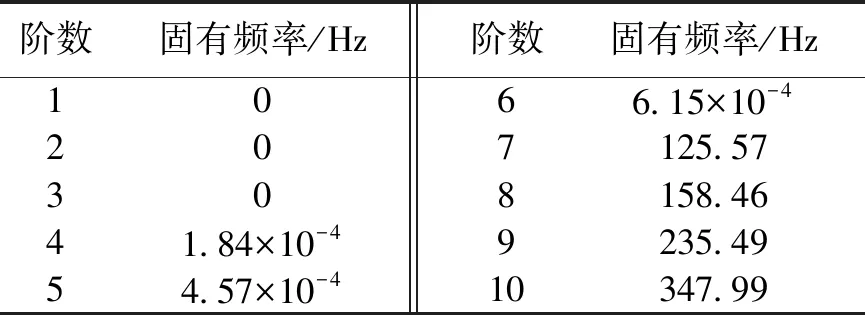
表 1刀盘前10阶固有频率Table 1 First ten order natural frequency of the cutter
从表1可以看出,刀盘的固有频率随阶数的增大而增大。
从刀盘模态振型(图3)中看出,7阶振型主要表现为刀盘两两相对的固定刀架沿Y轴方向上下摆动,其中振幅最小的位置出现在两固定刀架夹角的45°平分线处,形成两条节径,即a、b位置;最大振幅发生在4个固定刀架的最顶端处,约为2.717 5 mm,即A区域,变形百分比为0.566%(最大振幅/刀盘直径)。8阶振型主要表现为两固定刀架夹角45°线的位置沿Y轴方向上下摆动,其中,振幅最小位置出现在固定刀架内,并形成两条节径,即c、d位置;振幅最大发生在两固定刀架夹角45°线位置的最顶端,约为3.485 8 mm,即B区域,变形百分比为约为0.726%。9阶振型为刀盘4个固定刀架尾部整体沿着Y轴方向上下摆动,其中振幅最小位置出现在固定刀架内,振型云图可近似看做刀盘振型形成1条节圆,即e位置;振幅最大发生在4个固定刀架顶端和尾端,约为3.088 7 mm即C、D区域,变形百分比约为0.643%。10阶振型为绕Z轴的扭转变形,其中最小振幅出现在固定刀架夹角45°线位置和固定刀架内,形成3条节径,即f、g、h位置;最大振幅发生在靠近固定刀架附近,约为3.657 2 mm即E区域,变形百分比约为0.761%。

(a) 第7阶

(b) 第8阶
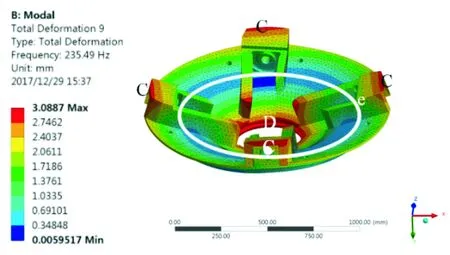
(c) 第9阶

(d) 第10阶图 3刀盘模态振型Fig.3 Vibration types of cutter modal
结合实际工况,以剥皮机刀盘最高转速1 000 r/min为例,根据f=n/60(f为频率,n为转速)计算得出,刀盘的共振频率为16.67 Hz,远远小于刀盘自身的固有频率,因此在切削金属棒料的过程中刀盘不会与机体发生共振,减小了刀盘故障发生概率。但从刀盘的振型来看,刀盘的7~10阶最大振幅值偏大,故要对原始刀盘系统进行优化。
2 刀盘结构的优化
2.1制定优化方案
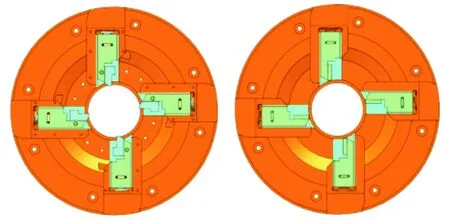
一般为降低机械结构的最大位移值是通过改变构件刚度(更换构件材料)或者在构件结构中增设加强筋或肋板等手段来实现。而本文所分析的刀盘结构最大相对振幅位置易出现在固定刀架之间且变形量较大,严重影响切削精度要求。由于铸铁是刚度较大的常用材料,故本文不更换刀盘材料,仅仅从刀盘结构方面来改善、解决变形问题。因此,本文对刀盘结构提出2种改进方案,图4(a),(b)为方案一,图4(c),(d)为方案二。方案一为在固定刀架之间增加沿刀盘直径方向的加强筋,并在加强筋上焊接固定板,即径向加强筋刀盘;方案二为在方案一的基础上增加横向加强筋,即纵横向加强筋刀盘。
2.2模态结果分析
对优化后方案一、二刀盘进行模态分析,优化后的刀盘7~10阶固有频率较原始刀盘固有频率有了明显的提升,方案二刀盘结构频率提升效果明显高于方案一,如表2所示。2种结构的振型描述与原始刀盘的振型描述一致,在每一阶模态振型中均出现了相同的节圆和节径数,并且出现的位置也基本一致,如图5,6所示。

(a) 方案一加强筋剖视 (b) 方案一刀盘外形 (c) 方案二加强筋剖视 (d) 方案二刀盘外形图 4刀盘优化结构图Fig.4 Optimizd structure of the cutters

(a) 第7阶 (b)第8阶

(c) 第9阶 (d)第10阶图 5方案一刀盘模态振型Fig.5 Vibration types of cutter modal scheme 1

(a) 第7阶 (b) 第8阶

(c) 第9阶 (d) 第10阶图 6方案二刀盘模态振型Fig.6 Vibration types of cutter modal scheme 2表 23种刀盘模态分析计算结果Table 2 Analysis and calculation results of three cutter modal
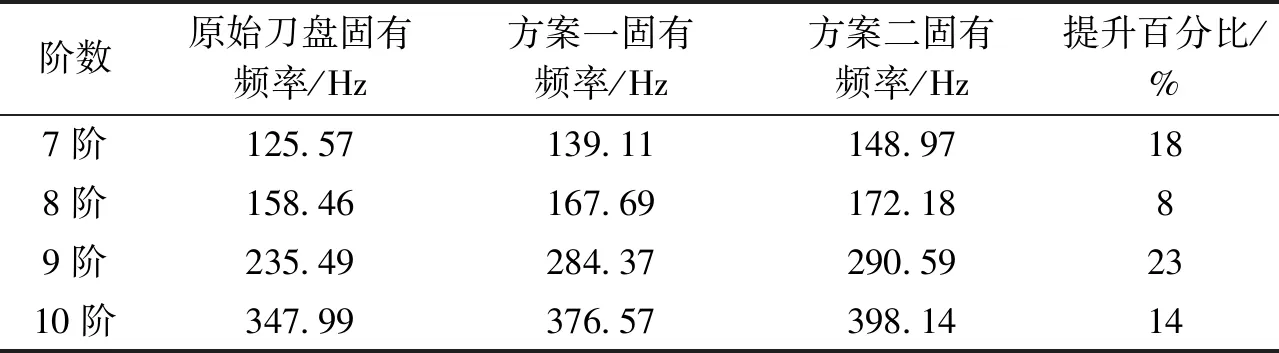
阶数原始刀盘固有频率/Hz方案一固有频率/Hz方案二固有频率/Hz提升百分比/% 7阶125.57139.11148.9718 8阶158.46167.69172.188 9阶235.49284.37290.5923 10阶347.99376.57398.1414
对比分析发现,方案一和方案二的第9阶模态振型固定刀架顶端均未出现最大相对振幅,区别于原始刀盘结构,并且方案一和方案二的最大振幅值均低于原始刀盘结构的最大振幅值。同时,与原始刀盘结构的模态计算结果相比,方案二的刀盘结构第7~10阶固有频率分别提升了18%,8%,23%,14%,如表2所示;方案二刀盘结构的固有频率值优于原始刀盘和方案一,并且满足实际工况的需求。综合来看,方案二的刀盘结构优于方案一和原始刀盘结构,故剥皮机刀盘的结构最后确定为方案二刀盘结构。
3 刀盘结构的静力学分析
针对整体的机械结构使用有限元法可准确分析结构应力、应变情况,进而优化机械结构[16]。因为对刀盘系统施加的载荷主要来自于切削时的切削反力,因此切削力是保证加工精度、优化刀盘结构的重要条件;同时,切削棒料的尺寸与切削厚度差异,导致刀盘系统零部件的应力、应变分布存在不同。因此本节主要分析剥皮机在切削Φ320 mm不锈钢棒料该种极限工况下刀盘零部件的应力、应变分布情况。为表达方便,在本文中规定剥皮机切削Φ320 mm的不锈钢棒料为工况一。
3.1静力学模型的建立
3.1.1 刀盘结构简化 在切削过程中,由于刀盘系统的零部件较多,并且有部分零件只担负传动的任务,不受切削力的作用,故可对刀盘系统进行结构简化,以求降低计算时间。因此,在优化后的方案二刀盘系统基础上建立刀盘结构的静力学模型,刀盘系统简化前后的模型如图7所示。
3.1.2 刀盘材料性能参数及网格划分 在建立模型时,刀盘系统零部件的材料性能参数设置如1.2.1节所示。材料参数设置完成后,分别添加刀盘系统零部件的性能参数,然后对刀盘系统进行网格划分。因为刀盘系统结构复杂,故选择网格类型为四面体单元[11],网格大小20 mm;总单元数为139 623,节点数为235 600。
(a) 简化前 (b)简化后 图 7 简化前、后的刀盘系统Fig.7 Cutter system before and after simplification
3.1.3 模型约束和载荷施加 根据实际工况对剥皮机刀盘系统模型添加约束和载荷。添加约束:刀盘是由8个螺钉固定于主轴齿轮上的,故采用Fixed Support对刀盘上螺钉孔施加固定约束力;对其他零件则设置为相应的接触关系,接触类型为No Separation。载荷施加:通过对不锈钢棒料切削时所产生的主切削力进行模拟计算来确定载荷(由于刀具直接固定在刀盘中的刀架上,因此不考虑其影响),进而来计算施加在活动刀架上的压力。通过对活动刀架结构的简化,能够计算出活动刀架上有效受力面积为43.5 mm×105 mm,即图8(a)中的红色区域,通过P=F/S(F为主切削力,S为有效受力面积,P为施加的压强力)来计算施加的压力,结果为3.9 MPa。故在刀盘系统4个活动刀架上分别施加4个切削反力,如图8(b)所示。
3.2刀盘系统静力学分析
材料HT250的强度极限σb为250 MPa,取安全系数n=3。当最大应力值小于材料的许用应力时,说明刀盘系统部件的强度满足工作需求[17-18]。
(1)
分析工况一可知,刀盘系统的最大应力值为16.3 MPa,图9(a),出现位置位于固定刀架末端,图9(b)。刀盘材料为HT250,其许用应力由式(1)计算为88.33 MPa,最大应力值远小于材料的许用应力值,刀盘系统强度能满足剥皮机切削不锈钢棒料的需求。
通过工况一计算的等效应变值能够看出最大等效应变值为0.000 1,图10(a),出现位置位于固定刀架末端,如图10(b)所示。通过应变分布云图能够发现,活动刀架内安装传动零部件部分的等效应变基本为零,这说明刀盘系统在工况一下运行时不会影响其调刀传动装置。刀盘系统极小的应变不会影响调刀系统的调刀精度,保证了剥皮机调刀系统的精确性。

(a) 刀架添加压力的范围

(b) 添加载荷后的刀盘系统图 8施载后的刀盘模型Fig.8 Cutter model after loading

(a) 工况一刀盘系统等效应力

(b) 工况一刀盘系统等效应力极值图
图9工况一刀盘系统的等效应力分布、极值图
Fig.9 Equivalent stress distribution and extreme value of cutter system in working condition one

(a) 工况一刀盘系统等效应变

(b) 工况一刀盘系统等效应变极值图图 10工况一刀盘系统的等效应变 分布、极值图Fig.10 Equivalent strain distribution and extreme value of cutter system in working condition one
4 结 论
(1) 通过模态分析,得到的刀盘低阶固有频率、振型及最大变形量。比较发现,纵横向加强筋刀盘结构(方案二)的第7~10阶固有频率较原始刀盘分别提升了18%,8%,23%,14%,有效优化了原始刀盘结构,降低了刀盘的最大相对位移值,增加刀盘刚度,使刀盘固有频率更加远离剥皮机工作的基频,以增加刀盘的抗振性能。为以后改进大型剥皮机刀盘结构参数提供参考。
(2) 运用ANSYS Workbench对纵横加强筋刀盘结构进行了静力学分析。刀盘在切削Φ320 mm不锈钢棒料这一极限工况时的最大应力和应变均满足剥皮机的工作需求,能够实现满足工作需求强度与自动调刀精确的刀盘系统。
