面向机器人抓取的零散工件识别与测量方法
2019-05-07林强强金守峰马秋瑞
林强强,金守峰,马秋瑞,张 浩
(1.西安工程大学 机电工程学院,陕西 西安 710048;2. 西安工程大学 服装与艺术设计学院,陕西 西安 710048)
0 引 言
随着现代先进制造技术的进步,工业机器人在生产加工过程中扮演着越来越重要的角色,并且不断地向着智能化和柔性化方向发展[1-3]。机器视觉使工业机器人具有了视觉感知的能力[4-5]。徐博凡等人基于FANUC机器人平台,研发了一套视觉引导系统,提高了机器人柔性化抓取能力[6];李鹏飞等应用双目相机作为引导,实现了机器人对织物的自动抓取[7];李振雨等应用神经网络算法,使用改进的Hebb学习规则提高了识别的精度[8];康存锋等应用机器视觉完成了对并联机器人的引导,实现了稳定可靠的抓取[9];韦攀东等人应用多关节机器人实现了柔软织物的抓取[10]。工业机器人对于固定未知的工件具有较好的抓取精度,但是,实际生产中,工件位置的随机摆放,将导致机器人抓取失败,影响工作效率。
针对工件位置随机摆放,影响抓取精度和效率等问题,提出了基于图像旋转和灰度投影的工件抓取方法。首先对采集的图像经过预处理后,用双线性插值法进行旋转校正,在得到的校正图后应用Canny算子提取零件的边缘,最后对边缘图像灰度投影,得到工件的测量尺寸,从而实现定位与测量。
1 旋转模型的建立
1.1旋转角
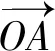

(1)
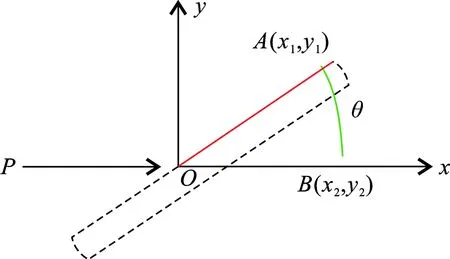
图 1夹角计算模型Fig.1 Angle calculation model
在实际的计算过程中,经过二值化和边缘检测等一系列预处理后,如图1所示长形工件的边缘则被置为1,其余区域则置为0。选取图形的中点P为起始点,向右寻找像素值为1的点,则该点为旋转基准点O,为避免图像噪声的影响,需要验证该点周围的像素点是否为1,若不为1则向下一行继续寻找,从而可确定基准点O的位置;得到O点后,向y轴的方向搜索,直到像素值变为0,则为A点的位置;B点为x正半上轴随机一点。
1.2旋转原理
在机器人抓取工件时,需要调整末端手爪的位姿来准确地抓取工件,提高抓取的精度以及效率。因此可通过建立旋转模型来求取工件与水平方向的夹角。图像旋转是一种常用的数字图像处理技术,已广泛应用于各个领域[11-12]。
由于在灰度投影时,投影的零件图像应处于水平或者竖直状态,因而需要对采集的图像做旋转校正处理。如图2所示,旋转是指将图像中所有的像素(基准点除外)按给定的角度沿着圆弧方向逆时针或者顺时针旋转。(x0,y0)是原始图像的坐标点,(x,y)是旋转后图像坐标点,R是(x0,y0)到原点的距离[13-15]。
根据图2中的三角关系可得

(2)
旋转后

(3)
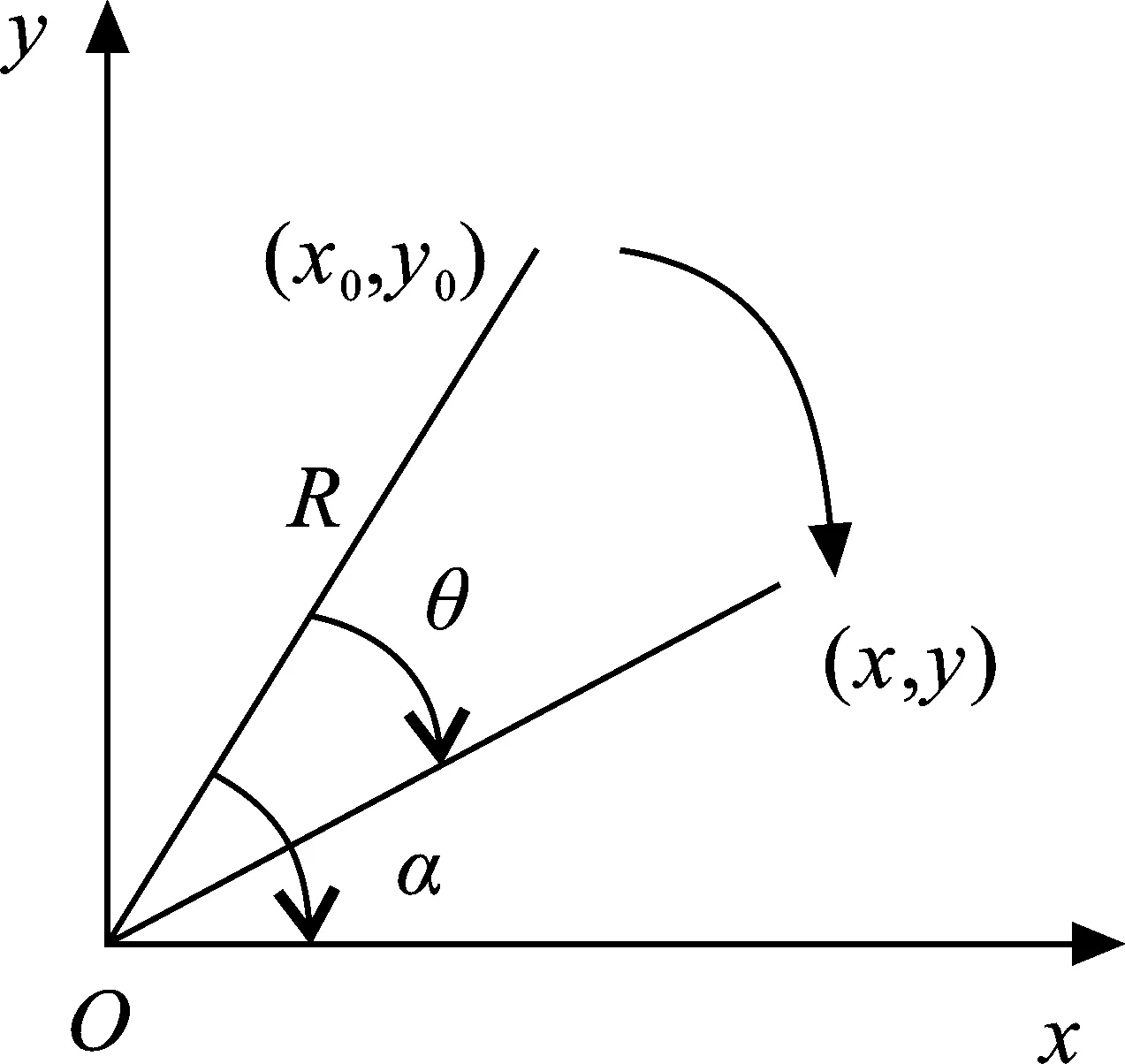
图 2图像旋转模型Fig.2 Image rotation model
联立式(2),(3)后写成矩阵形式
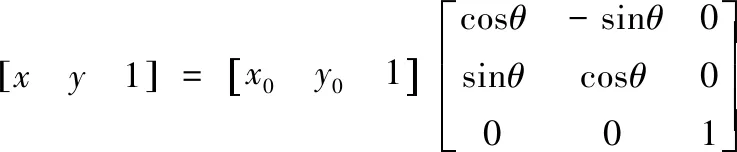
(4)
在进行位图旋转时,确定旋转后的位图大小后,可以确定旋转之后位图矩形区域,需要访问该区域的每一个坐标,以获得该坐标对应于源位图的坐标,最后获得该坐标对应于原位图坐标点处的像素值。因此,在得到式(4)的旋转矩阵后,需要做逆运算,逆运算矩阵如式(5)所示。
(5)
由于图像坐标系原点在左上角,因此需要与实际数学坐标系进行坐标系转换。假设位图的宽度和高度分别为W和H,则图像坐标(x0,y0)与数学坐标(x,y)的关系为
(6)
逆运算关系为
(7)
旋转需要再将数学坐标转换为图像坐标,设旋转后图像的宽度和高度分别为W1和H1,则旋转矩阵和逆运算矩阵为
(8)
(9)
整个旋转过程为:(1)将原始图像的坐标转换为数学坐标;(2)通过旋转公式将图像进行旋转;(3)将旋转后的数学坐标转换为图像坐标。
旋转过程矩阵变换为
(10)
式中:A=-0.5Wcosθ+0.5Hsinθ+0.5W1;
B=-0.5Wsinθ-0.5Hcosθ+0.5H1.
由于旋转后图像的坐标不是整数,故旋转后必须对像素点灰度进行插值运算。常用的插值方法有最近邻法、双线性插值法和双三插值法等3种[16-17]。最近邻插值法操作简单,运算速度高,但效果较差,图像容易模糊;双三插值法速度慢,但图像质量很高;综合比较后,本文采用比较适中的双线性插值法,对图像进行插值运算。
双线性插值原理如图3所示,利用(X,Y)处邻近的4个灰度值,计算(X,Y)处的灰度值。设4个邻近像素,为A,B,C,D,其坐标分别为(i,j),(i+1,j),(i,j+1),(i+1,j+1),灰度值分别为g(A),g(B),g(C),g(D),首先计算E,F点处的灰度值g(E) ,g(F)

图 3双线性插值Fig.3 Bilinear interpolation g(E)= (X-i)[g(B)-g(A)]+g(A)= (i+1-X)g(A)+ (X-i)g(B)
(11)
g(F)= (X-i)[g(D)-g(C)]+g(C)=
(i+1-X)g(C)+
(X-i)g(D)
(12)
则(X,Y)处的灰度值为
g(X,Y)= (Y-j)[g(F)-g(E)]-g(E)=
(j+1-Y)g(E)+
(Y-j)g(E)
(13)
经过计算,图1中的图像与x轴的夹角为32.149 3°,将此图像经过旋转校正后得到水平的轴边缘检测图。
2 基于灰度投影的尺寸测量
经过旋转后的图像与水平方向的夹角近似于0°,为了快速得到工件的尺寸,因此采用灰度投影的方法测量轴径。灰度投影算法是利用图像灰度曲线进行图像分析的一种方法,由于只需对图像行列做投影运算,因此,在减少计算量的同时也提高了运算速度。设经过旋转校正后的图像为I(x,y),大小为M×N,按式(14)对其进行图像行、列像素灰度值累加投影[18-19]。
(14)
式中:fk(i,j)为图像中(i,j)点的灰度值;Ck(j)为图像中第j列像素灰度值的累加投影;Rk(i)为图像中第i行像素灰度值的累加投影。对校正后轴边缘检测图像做行投影,得到图4的投影曲线。从图4可得,投影曲线的峰值位置即为轴的边缘处,计算两峰值位置的坐标差值,即为轴的直径大小。

图 4投影曲线图Fig.4 Projection curve
3 实验分析
3.1实验平台与视觉标定
Dobot机械臂、工业相机及计算机搭建的机器人视觉抓取实验平台如图5所示,Dobot机械臂为四轴四自由度的机器人,手爪为气动机械手爪,滑轨有效行程为0~1 000 mm,Dobot机械臂通过支撑板安装在滑轨上,可实现移动抓取。工业相机为AVT-GE相机,分辨率为1 024×1 024,最大帧频为59帧/s,使用镜头为Computar手动光圈镜头,焦距25 mm。
通过以上计算所得的数据都以像素(pixel)为单位,因而需要通过相机标定转换为以mm为单位的数值。实验过程中,首先采集不同尺寸的标准量块。假定量块为P(mm),经过图像处理之后得到相应像素数为M,可计算物面分辨率K=P/M。采用20 mm,30 mm,40 mm,50 mm的量块进行标定,实验之后以计算出多组物面分辨率的平均值作为机器视觉系统的物面分辨率。标定实验数据如表1所示。

图 5机器人抓取系统Fig.5 Robotic grab system表 1标定实验数据Table 1 Calibration experiment data
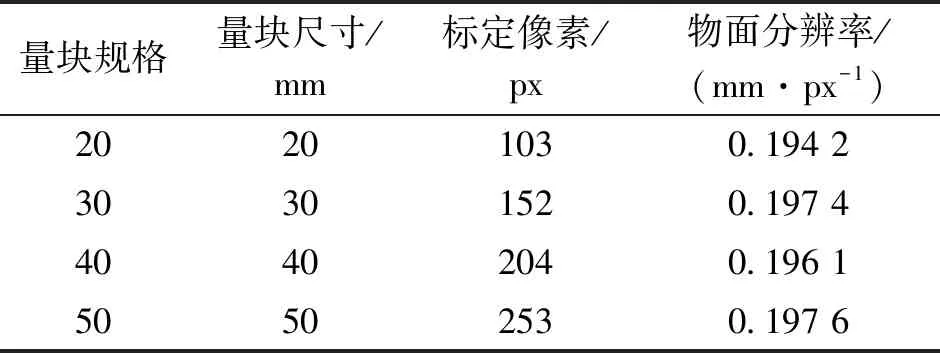
量块规格量块尺寸/mm标定像素/px物面分辨率/(mm·px-1) 20201030.194 2 30301520.197 4 40402040.196 1 50502530.197 6
根据表1中标定的物面分辨率,计算得到物面分辨率的均值K:
0.196 3(mm/px)
3.2旋转校正

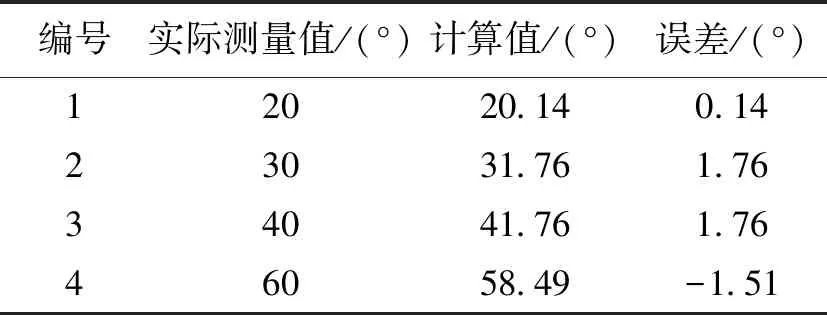
表 2夹角计算Table 2 Angle calculation result
由表2可知,建立的旋转模型校正误差保持在±2°以内。由于采用灰度投影的计算方式,累加投影曲线对于图片的旋转误差并不敏感,因此建立的旋转模型可以满足本文的计算要求。其中20°和60°的轴旋转结果如图6所示。

(a) 20°工件原始图 (b) 旋转校正图

(c) 60°工件原始图 (d) 旋转校正图图 6部分工件校正图Fig.6 Correction chart of parts of the workpiece
从表3可以看出,除编号2的轴径测量值超出了实际的轴径误差外,其余测量值均在误差范围内。实际测量值与计算值的误差也保持在0.2 mm以内,在精度要求不高的生产环境中,可以满足实际识别与定位要求。
在工件的识别与定位过程中,对于旋转角的计算存在±2°的误差,因而导致在投影计算峰值时出现了误差,计算值与实际的轴径误差经过计算为0.134 1 mm。而在机器人识别抓取的过程中,这个误差可以满足抓取要求,并不会影响抓取精度,因而本文提出的方法可以应用于实际生产。
4 结 论
(1) 建立了旋转校正模型,在提取散放工件边缘轮廓特征点的基础上,通过坐标转换、双线性插值计算工件与水平方向的夹角,实现工件的校正。所得夹角可用于机器人手爪位姿的调整,便于快速抓取。
(2) 提出了工件尺寸测量的灰度投影方法,对校正后的工件边缘轮廓进行行投影,查询投影曲线的峰值,峰值点所对应的像素坐标差值为工件的像素尺寸,结合标定参数得到实际尺寸,根据工件尺寸进行机器人手爪开合大小的调整。
(3) 以Dobot机械臂构建了机器人视觉抓取实验平台,对本文方法进行验证,实验结果表明该方法校正角度的误差控制在2°以内,测量尺寸误差控制在0.5 mm以内,达到机器人末端手爪的位姿和手抓开合的调整精度。
