170SD30陶瓷电主轴动力学建模及振动响应分析*
2019-05-07石怀涛赵纪宗
石怀涛, 赵纪宗, 张 宇
(沈阳建筑大学 a.机械工程学院;b.高档石材数控加工装备与技术国家地方联合工程实验室,沈阳 110168)
0 引言
高速电主轴作为数控机床加工的核心部件,是先进制造技术的载体,其各项工作性能的好坏将直接影响着数控机床甚至整个制造业的发展。随着高速电主轴向高转速、高精度、高效率方向的发展,对电主轴本身和电主轴的动力学特性也提出了更高的要求[1-3]。电主轴在高转速情况下运行时会不同程度的产生离心力、惯性力和各种不平衡响应,当外界激振力的频率和电主轴的固有频率相接近或者相等时,主轴系统就会发生共振,这将会严重影响加工零件的加工精度和质量。高性能结构陶瓷作为高速主轴轴承及主轴材料,可以充分发挥陶瓷材料密度小、耐高温、耐磨损、高强度等优良性能,最大程度的降低电主轴在高速旋转时产生的离心力、惯性力以及各种不平衡响应,大大的提高电主轴的运转精度[4-5]。因此,“高转速、高精度、高效率及小振动”成为陶瓷电主轴应用的巨大优势。
目前常用的研究高速电主轴动力学特性的方法主要有以下三种方法:集中参数法、传递矩阵法和有限元法[6-9]。集中参数法将系统简化为互相影响,互相作用的多刚体系统,将质量分散生成包含系统动力耦合特性的集中参数模型;传递矩阵法是把复杂的线性系统分割为若干个元素,用矩阵来描述各个元素之间的特性,用这些矩阵的乘积即可表示整个系统的特性,在利用两端的边界条件,就可以求得系统的动态特性;有限元法首先是将弹性系统分割为若干个元素,把系统离散化之后建立起各个单元之间的运动方程,再以单元的节点位移函数来表示单元内的位移特性,从而导出质量矩阵、刚度矩阵和整个系统的运动方程式,求得系统的动态特性。其中集中参数法在实际中运用的比较少,而有限元法随着计算机技术的发展能够快速准确的求出转子的临界转速,但是使用有限元法对计算机硬件要求极高且占用内存大[10-11];传统传递矩阵法以程序简单、耗时少和所需内存小的优点,被广泛的应用,但是随着计算频率的提高,运算的精度降低[12]。
近年来,电主轴动力学特性在主轴工作中的重要影响引起了国内外专家的研究热潮,并取得了比较突出的成果。殷国富等[13]、陈小安[14]、王建平等[15]以及Jorgensen B R等[16]分别使用有限元仿真和影响系数法对电主轴的动静态性能进行了分析,且综合考虑各个耦合系统之间的关系提出了新型电主轴的耦合动力学模型,但在计算时不同程度的对轴承载荷和变形关系进行线性简化,且是集中在动态模型的建立及分析产生振动的机理。
本文采用采用Riccati法建立电主轴动力学理论模型,使用Matlab编程Riccati法和Prohl法计算电主轴固有频率与临界转速,将仿真结果与锤击法试验结果对比,验证了Riccati法建立的170SD30电主轴理论模型的准确性,并分析相同转速不同节点和不同转速下不同节点上轴系的不平衡响应;同时运用有限元ANSYS对电主轴进行谐响应分析,研究不同的预紧力对主轴振动性能的影响。
1 高速电主轴动力学建模
传递矩阵法首先将高速电主轴简化为集中参数力学模型,在简化过程中,按照质心不变的原则,在尽量保持高速电主轴所有动力学特性的前提下,将高速电主轴系的转子系统简化成为由集中质量和若干轴段组成的模型[17]。
1.1 模型简化
电主轴是新一代机、电、液一体化的加工中心用高速精密主轴,主要由壳体、主轴、轴承、定子和转子等零件组成[18]。图1给出了170SD30 型电主轴的结构示意图,其前后轴承均采用角接触球轴承,主轴前端轴承型号为7015C,后端型号为7012C。

图1 170SD30电主轴结构图
主轴的支撑一般采用角接触球轴承,由于存在初始预紧力,会使其所承受的工作载荷能力和主轴刚度有所提高。因此,在简化电主轴模型时需要考虑轴承的刚度。轴承的刚度可以分为径向刚度、轴向刚度和角刚度,在实际工况下,随着转速的提高轴向刚度和角刚度都会达到一个较为稳定的值,对电主轴的动力学特性影响很小[19]。所以在简化高速电主轴模型时轴承可以简化为4个径向均布的弹簧,只考虑其径向刚度,简化后如图2所示。在添加轴向预紧力的情况下,径向刚度的计算公式为[20]:
(1)
其中,δ为角接触陶瓷球轴承修正系数;Db为滚动体直径(8mm);Z为轴承滚动体数目(18个);α为接触角(150);Fa0为轴向预紧力,本文研究的电主轴是轻载取δ=1.8,前后预紧力都是400N。代入上式得Kr=2245.42N·mm-1。
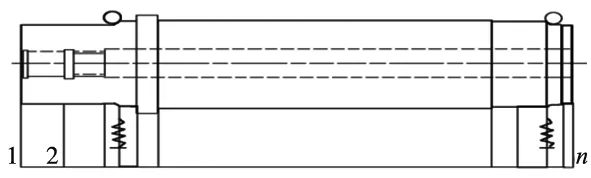
图2 电主轴实体简化模型
1.2 节点划分
在使用传递矩阵法对高速电主轴进行模型简化时,需要对电主轴进行节点划分,而节点的数目将会严重影响电主轴临界转速的计算结果,其中节点数太少计算结果不精确;节点数太多会导致计算过程复杂,耗费时间长,误差增大。根据等截面梁的计算结果,如果要求计算的高速电主轴的临界转速误差小于1%,那么节点总数N应满足如下关系[21]:
N≥1+5.34r
(2)
式(2)中,r为要求计算的主轴固有频率(或临界转速)的最高阶数,根据转子模型,电主轴被划分为25个节点,则r=4。建立的电主轴的简化力学模型如下图3所示。

图3 电主轴的简化力学模型
2 Riccati传递矩阵法对电主轴的分析计算
2.1 传递矩阵法基本原理与计算方法
Riccati传递矩阵法建立的新型高速电主轴模型计算主轴的临界转速时,在编程时考虑了剪切效应和截面系数等影响因素,计算结果更精确,计算速度更快[22]。
在构建电主轴的传递矩阵时,为考虑剪切效应的影响,要在矩阵中加入剪切影响系数 :
(3)
式中,E为弹性模量,I为截面对中性轴的惯性矩,kt为截面系数,G为材料剪切模量,A为截面积,l为轴段的长度。
由材料力学,截面系数:
(4)
式中,x为不均匀分布系数,是一个无量纲系数。计算公式如下:
(5)
(6)
通过式(5)和式(6)计算可以得到,不均匀分布系数x与电主轴的截面形状有相关。其中圆形截面,x由内外径的比值确定,具体关系如表1所示。在本文中,170SD30 型电主轴为实心即是内外径比值为d/D=0.5,因此x取值1.69。

表1 内外径的比值与不均匀分布系数的关系
Riccati传递矩阵法的计算原理是:首先把轴划分为若干等质量的轴段,然后根据轴段两端的边界条件,从轴的一端逐步递推到另一端,从而确定起始端的状态向量,在反过求各个截面的状态向量;在转速由小变大的过程中,响应最大的点即为临界转速[23]。
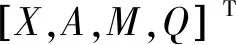
Ti=
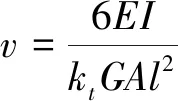
Riccati传递矩阵法把每个节点Z的状态矢量的r个元素分成f和e两组,即:
(7)

(8)
式中,

将式(8)展开,得:
(9)
引入如下Riccati变换:
fi=Siei
(10)
式中,Si称为Riccati矩阵,它是一个r/2×r/2的方阵,将上式代入(8)得:
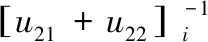
(11)
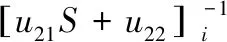
(12)
对比式(10)和式(12),可知:
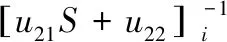
(13)
这就是Riccati传递矩阵的递推公式。
由起始截面的边界条件知f1=0,e1≠0,故有初值S1=0。在已知u11、u12、u21、u22的条件下,反复利用式(13),就可以顺次递推得到S1、S2......、Sn。
对于右端截面N+1的节点则有:
fN+1=SN+1eN+1
(14)
由右端的边界条件fN+1=0及eN+1≠0,故式(14)有非零解的条件为:
(15)
这就是系统的频率方程式。满足式(15)的根ω即为所求的临界转速的角速度。
2.2 主轴系统的不平衡响应分析
质量不平衡响应是主轴系统振动响应分析中非常重要的一个环节,在实际情况下,由于转子材质不均、加工误差及安装偏差等原因,轴系总是存在质量不平衡,因此分析主轴系统的不平衡响应是非常重要且有意义的。
初始输入电主轴的结构参数如下:定子外径D1=130mm,定子内径D2=80mm,轴端长度l=11mm,支撑刚度Kr=2245.42N·mm-1,单元质量m=6.0×10-9t/mm3。其中轴段材料参数入下:弹性模量E=20600N·mm-2,泊松比μ=0.3,密度ρ=7.85g·cm-3。输入转子系统结构参数和材料参数后,调用函数计算单元的5个特征值:质量m、极转动惯量Ip、直径转动惯量Id、弹性模量与截面对中性轴的惯性矩的乘积EI以及剪切影响系数。
运用Matlab编写Prohl法、 Riccati法的程序,可以求得转子各阶固有频率和临阶转速具体算法流程图如图4所示,求解得前4阶固有频率对比结果如表2所示。

图4 算法流程图

阶数Riccati法Prohl法固有频率/Hz误差/%11667.91661.56.022058.12032.58.232956.52890.29.344193.23866.17.8
从表2中可以得到Riccati法比Prohl法计算的固有频率值更大,且两者最大误差为9.3%,后面将计算仿真结果于实验结果进行对比。
根据Riccati传递矩阵法的基本原理,假设主轴系统轴系上存在着偏心质量0.1kg,偏心距0.005m,工作转速为3000r/min。运用Matlab编制程序计算偏心质量处于不同节点时的不平衡响应,不平衡量加在节点3,10,14,15,20,24上,仿真结果如图5所示。

(a) 节点3 (b) 节点10
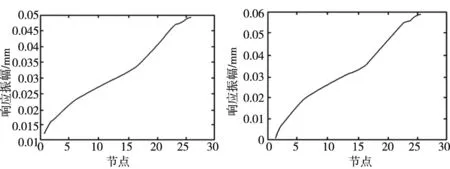
(c) 节点14 (d) 节点15
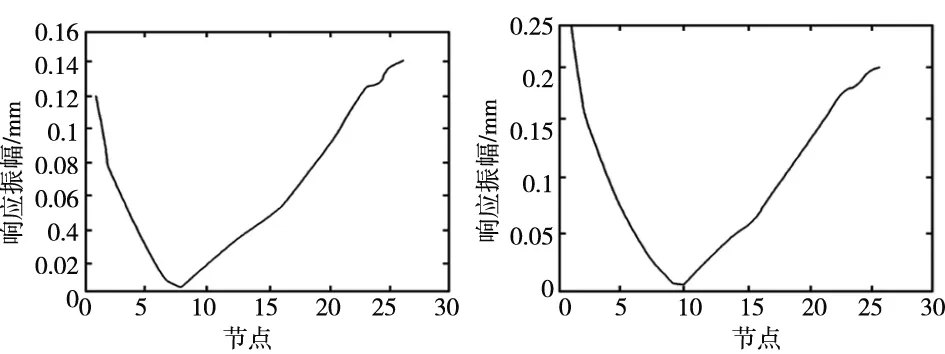
(e) 节点20 (f) 节点24 图5 不同节点上相同转速下轴系的不平衡响应
可以看出,轴系两端弹性支撑附近(节点3和节点24)对不平衡量很敏感,即是如果发生不平衡,响应的振幅最大。
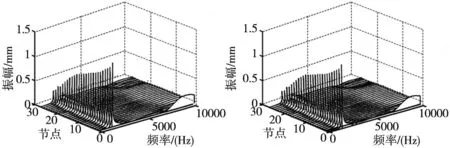
针对不平衡量加在节点3,10,14,15,20,24以上几种不平衡分布情况,采用Riccati传递矩阵法计算不同转速下的响应结果 ,如图6所示。由图可以看到主轴转速从0r/min逐渐增大的过程中,整个轴系的不平衡响应,其中频率在接近1600Hz和3100Hz处各点的振幅突然增大,说明轴系发生了共振。

(a) 节点3 (b) 节点10
(c) 节点14 (d) 节点15

(e) 节点20 (f) 节点24 图6 不同节点上不同相同转速下轴系的不平衡响应
3 实验分析与结果讨论
为了验证Riccati传递矩阵法仿真结果的正确性,搭建了高速电主轴动态性能测试系统。本实验采用锤击法对170SD30 型高速电主轴进行敲击,并对输入输出信号进行激振和采集。实验设备包括力锤、电荷放大器、加速度传感器、力传感器、信号采集仪等。实验测试流程图及实验平台如图7和图8所示。
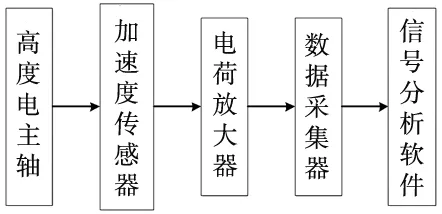
图7 电主轴动态性能测试流程图

图8 电主轴动态性能测试系统
在电主轴上所安装的传感器是加速度振动传感器,是采集振动信号的主要设备,通常由质量块、阻尼器、弹性元件、敏感元件和适调电路等部分组成。本套实验设备的传感器主要参数如表3所示。

表3 传感器主要参数
为了降低实验误差,得到更准确的实验数据,本实验主要选取3个锤击点,分别是主轴前段,主轴中部和主轴后端。实验方法为单点响应,多点施振,具体步骤如下,首先,启动主轴,从某一低速开始运行,然后,用力锤对每个测点敲击6次,力锤加在主轴前端的冲击力为100 N,其次,按一定的步长逐步提高转速,同时对每种转速下电主轴的振动响应值进行测量并记录,最后,获得电主轴振动响应值曲线,如图9所示。

图9 电主轴振动响应曲线
由图9得到1767.6Hz、2214.0 Hz、3186.6Hz分别为主轴的前3阶频率,其余的波峰为电磁噪声的干扰振动频率。Riccati传递矩阵法得到的电主轴前三阶固有频率分别是1667.9 Hz、2058.1Hz、2956.5Hz,最大误差不超过7.2%,比传统传递矩阵法精度提高了2.1%。由此证明了Riccati传递矩阵法分析电主轴的准确性和可行性。
4 预紧力对轴系振动的影响
轴承预紧力对主轴系统的固有频率、振动、刚度、轴承温升等具有重要影响。如果能对主轴系统施加合适的预紧力,它能够有效提高轴系的固有频率、轴系刚度,降低轴系振动,对于提高主轴系统的运行性能具有重大意义。
在ANSYS中有三种谐响应分析方法:完全法、缩减法和模态叠加法。其中综合考虑计算效率、方法特点及主轴系统的具体情况,本文采用模态叠加法进行谐响应分析计算[24]。
在激振力的作用下,当激振力的固有频率和电主轴的固有频率相等时,在电主轴的固有频率处会发生共振并产生响应位移。本文主要对不同预紧力下轴系一阶频率的响应位移进行了计算分析,选取初始激振力F=50N,加载在主轴前段。具体分析步骤如下:
⑴在对模拟轴承的弹簧处施加阻尼。对前轴承的模拟弹簧施加阻尼为1.17N·s/mm,对后轴承的模拟弹簧施加阻尼为 0.765N·s/mm。
⑵计算初始预紧力为50N时电主轴的固有频率。根据轴承径向刚度计算公式(1),对前后轴承的轴向弹簧施加刚度为Kr=2245.42N·mm-1。通过有限元软件首先计算出轴系相应的固有频率,之后再计算出在此固有频率下的轴系谐响应,并分别记录轴系前端、中间和后端的谐响应位移。
⑶重复步骤⑵分别求当对轴承施加预紧力为100N、150N、200N、250N、300N、350N、400N时,主轴前端、中间和后端的谐响应位移。
根据以上步骤可以得到当主轴在不同预紧力下作用时,主轴前端、主轴后端和主轴中间的径向响应位移,如图10~图12所示。
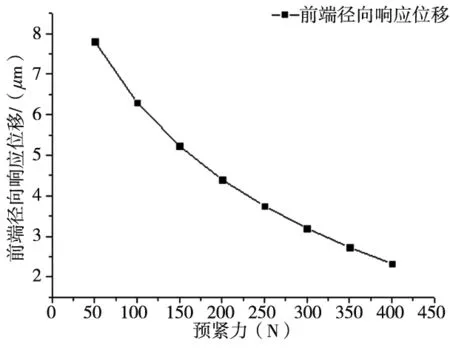
图10 主轴前端径向响应
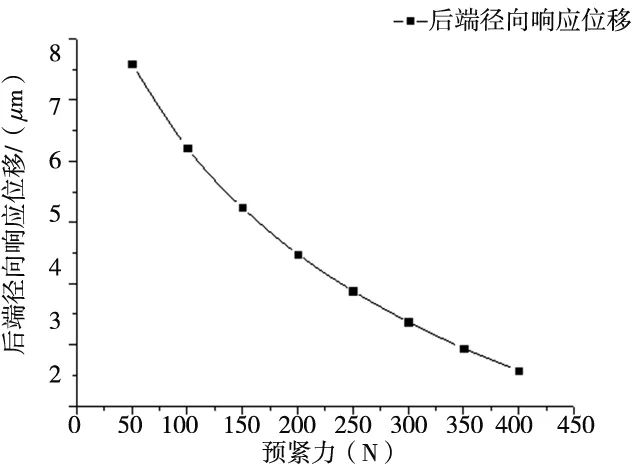
图11 主轴后端径向响应位移

图12 主轴中间径向响应位移
从图10~图12中可以得到,主轴前端和后端的径向响应位移随着预紧力的增大而减小,主轴中间的径向响应位移随着预紧力的增大而增大。由此可以得到对轴承施加合适预紧力能够降低主轴前端和后端的振动,且在主轴轴承等弹性支撑附近施加的预紧力要比在非弹性支撑处施加的预紧力大,有助于降低振动位移,这对指导研发高性能电主轴具有重要意义。
5 结论
(1)Riccati传递矩阵法求得的电主轴的固有频率和临界转速与实验结果最大误差为7.2%,比传统矩阵法精度提高了2.1%,证明了Riccati传递矩阵法的准确行与可行性,解决了传统传递矩阵法运算精度降低的问题。
(2)电主轴在运转过程中,在轴系的弹性支撑附近对不平衡量比较敏感,响应的振幅较大,易发生共振。
(3)适当增加预紧力能够降低主轴前端和主轴后端的振动,可以有效的避免由于振动带来的影响。
