基于GA-IPSO算法的柔性生产线高级计划排程方法研究*

2019-05-07吴永明张晗徐艳霞赵旭东

组合机床与自动化加工技术 2019年4期

吴永明，张晗，徐艳霞，赵旭东

(贵州大学现代制造技术教育部重点实验室，贵阳 550025)

0 引言

高级计划排程(APS)是一种包含了众多数学模型可以有效提高排程效率的生产线排程方法，可以有效解决企业遇到的多任务、多工序的生产排程问题。

目前，大部分学者针对高级计划与排程问题的研究主要集中在构造模型及求解算法等方面。宁维巍等分析了APS技术在这两种生产管理下的应用情况[1]。黄健等提出了一种面向多品种小批量混装线的高级计划排程模型[2]。Krenczyk等提出了一种集成物料规划系统与高级计划排程系统的排程模型，通过可视化方法来进行生产计划排程[3]。Bhawarkar等提出一种减少机器闲置时间和拖期惩罚高级计划排程方法[4]。Ornek针对制造资源计划系统无法考虑车间容量变换的问题，提出了基于约束规划建立的高级计划排程模型[5]。Marcosiris等提出了一种基于瓶颈分配方式的高级计划排程模型以减少其在瓶颈问题中的影响[6]。Kenn等针对供应链设计了高级计划排程系统，体现了排程系统的智能性[7]。James等针对设备负荷设计出一种根据零件工艺自动分配生产线的高级计划排程系统[8]。刘晨等构造了高级计划排程模型并采用不等长矩阵的编码方式的遗传算法求解，但易在陷入局部最优[9]。范营营等设计了一种启发式算法缩短产品在车间的流动时间，提高了资源利用率，使派工层面科学化、正规化[10]。张腾飞等提出一种改进遗传算法求解作业调度问题[11]。

然而，大部分学者对于APS模型的建立忽略了实际生产过程中，生产力较为不足或要求更快的交付定单等情况。针对上述问题，本文基于混合整数规划，以最小化完工时间、降低生产成本为生产线排程优化目标，建立高级计划排程模型。在模型中将部分工序外包以解决由于生产能力不足导致订单无法按时交付的问题。设计了一种GA-IPSO优化算法求解高级计划排程模型，在粒子的寻优搜索过程当中实时动态地改变惯性权重值，并对粒子进行交叉、变异等操纵以增添粒子的多样性，提升优化算法的计算精度和寻优搜索能力，防止优化结果陷入局部最优。通过实例验证了高级计划排程模型及优化算法在提高企业排程效率问题上的有效性。

1 基于混合整数规划的高级计划排程模型

1.1 模型描述

及时可靠地交付订单产品是制造型企业提高市场竞争力的基本条件，是生产线调度排程的重要目标之一。当企业因控制成本或生产能力限制无法按时完成订单时，将生产过程中的部分工序外包成为一种合理的选择。因而，结合混合整数规划，创建一种基于高级计划和排程方法的优化模型。图1为高级计划排程优化模型的示意图。

图1 排程模型示意图

1.2 模型的假设条件

(1)机器间相互独立，不存在先后关系；

(2)机器在某一时刻只能加工一个工序任务；

(3)每台机器具有固定且已知的准备时间；

(4)机器在开始加工零件之后无法停止；

(5)机器单次只可加工某一道工序；

(6)零件在机器上的加工时间已确定。

1.3 参数和变量说明

Oi：订单(i=1,2,...,o)，其中：o为订单数量；

Si：订单Oi中未外包工序的总加工时间；

Di：订单Oi中外包工序的总加工时间；

DTi：订单Oi中外包工序的运输时间；

Mr：零件编号(r=1,2,...,R)，其中：R为零件数量；

Nj：工序编号(j=1,2,...,J)，其中：J为工序数量；

rk：机器准备时间。

1.4 模型构建

(1)

Si,Di,DTi≥0,∀i.

(2)

rk>0

(3)

其中，公式(1)为以最小化订单总完成时间为目标的函数；公式(2)限定订单完工时间，运输时间均为正数；公式(3)限定机器准备时间为正数。

2 基于GA-IPSO算法的APS模型求解

采用粒子群算法求解APS优化模型。该算法具有操作简便、精度高、收敛快等优点，但是存在容易陷入局部最优等问题。对此，加入遗传算法中的交叉和变异等功能以提高算法的全局和局部意义下的搜索能力和效率。

2.1 粒子群算法

粒子群算法中的每一个粒子均具备两个属性：速度V和位置X。速度表示粒子搜索的快慢，位置表示粒子搜索的方向。粒子在解空间中独立地搜索最优解，并将其记为当前个体极值Pbest。将当前个体极值与粒子群中其他粒子相比较，得到最优个体极值设为粒子群的全局最优解Gbest。粒子群中的全部粒子依据寻优得到的个体最优解Pbest和全局最优解Gbest来调整粒子自身的速度和位置。速度与位置的更新公式为：

(4)

(5)

式中，ω为惯性权重，以保持原本速度；C1为粒子追踪历史个体最优解的权重系数；C2为粒子追踪粒子全体最优解的权重系数；ξ，η为[0，1]区间均匀分布的随机数。图2为基本粒子群算法的流程图。

图2 基本粒子群算法流程图

2.2 GA-IPSO算法

图3 遗传-粒子群算法流程图

2.3 算法步骤

2.3.1 初始化粒子种群

由于基本粒子群算法属于连续寻优过程，而生产线的工序排程为离散过程，因此必要对粒子进行某一方式编码，用以拟定不同零件及不同工序之间的加工顺序优先级。对于m个零件，n道工序，其对应的粒子长度为m×n，每一道工序对应一个10～30范围内的随机数。与工序对应之随机数执行倒序排序，排序优先级表示该工序加工优先级。

2.3.2 目标函数

2.3.3 更新粒子的速度和位置

惯性权重是基本粒子群算法中更新粒子自身寻优速度的最重要的参数。较大的设定值利于提升算法的全局寻优能力，较小则增强算法的局部寻优能力。基本粒子群算法的惯性权重通常采用固定值，但其缺点在于寻找最优解的过程中，粒子群的多样性容易随着迭代过程而逐步降低，从而导致结果陷入局部最优。现加入一种动态改变惯性权重的方法，用来保持粒子群在迭代过程中的多样性，避免结果陷入局部最优。各代的惯性权重表达式为：

“妙在似与不似之间”，这是老观念，传承就是要像，不像就不叫传承，首先是传承，或者叫继承，才能谈得上创新。先要走入，方能走出。连老师的皮毛都没有学到，形与神都学不像，谈何创新？只有学不像老师的人，才天天说要创新，因为学不会老东西，只能讲创新。真正的学生，通常都会说，一辈子连老师的皮毛都没有学到，这不能理解为谦辞。

(6)

式中，gn为迭代次数；gnmax为最大迭代次数；ωs为初始惯性权重，取1.2；ωe为迭代至最大次数时的惯性权重，取0.4。

同时，为增加粒子的收敛性，现加入速度限制范围。设置编码后产生随机速度范围的0.25倍，即粒子的速度区间。分别按公式(4)、式(5)重置粒子的寻优速度和位置。

2.3.4 粒子的交叉

现将遗传算法中的交叉增添至粒子群算法的搜索过程中。采用随寻优搜索过程动态变化的交叉概率以增加交叉粒子的多样性。计算公式为：

(7)

式中，pc为交叉概率；pcmax为最大交叉概率，取1；pcmin为最小交叉概率，取0.5。采取两点交叉法以及随机抽取交叉法进行交叉操作。生成一个[0，1]区间内随机数，若其小于0.5，则采取两点交叉法；否则，采取随机抽取交叉法。两点交叉法操作如下：

(1)从全部粒子中随机选取两个粒子作为父代粒子进行交叉操作；

(2)随机生成两个交叉点并保证交叉长度界限大于粒子总长度的1/3且小于粒子总长度的2/3；

(3)将所选取的两个粒子中，位于两交叉点之间的部分进行交换，生成两个新的子代粒子，交叉结束。

随机抽取交叉法操作如下：

(1)从全部粒子中随机选取两个粒子作为父代粒子进行交叉操作；

(2)生成与粒子相同长度的list列表，列表中随机排列元素1和2；

(3)将第一条粒子中与list列表中元素1所在位置对应的位置中的元素提取出，将第二条粒子中与list列表中元素2所在位置对应的位置中的元素提取出，组成一条新的粒子；

(4)将上述操作执行两遍，生成两条新的子代粒子，交叉结束。

2.3.5 粒子的变异

粒子群算法的变异过程为：基于轮盘赌选择法，随机抽取种群中某一粒子；生成一个(0,1)间的随机实数r，若r小于变异概率pm=0.1，则经由编码方法随机产生新粒子替换之前粒子；否则，依次对下一粒子执行上述操作。

2.4 GA-IPSO算法的特点

(1)粒子群算法采用速度和位置更新公式来重置各代粒子，遗传算法即不断经由父代染色体间的交叉得到子代。两种算法的联合,可以有效地增强粒子的全局寻优能力、速度以及精度。

(2)粒子群算法参数选择要求较低，而遗传算法则对参数要求较高，两算法的结合可以在不影响优化性能的前提下降低对于参数设置的要求。

3 算例验真与分析

结合某一制造型企业接到的客户订单来验证高级计划排程模型及求解算法的有效性。订单包括6个零件，每一个零件需要6道工序来完成，订单要求总完成时间低于320min，现有共5台机器来完成该订单。各台机器的准备时间分别为20，10，10，15，20min。表1为各零件的各道工序制造时间，表2为各零件的各道工序所属加工机器的编号。

表1 各工序制造时间(单位：min)

表2 各工序所属加工机器编号

经由基本粒子群算法和遗传-粒子群算法分别对高级计划排程模型进行求解，参数设定为：种群规模100；迭代次数100次；c1,c2为2.05；终止条件即迭代次数。两种算法均由Matlab软件编程实现。将数据代入可得到各工序最优加工顺序甘特图及最短加工完成时间。图4为3种情况下的寻优过程对比图。表3为实验结果对比。

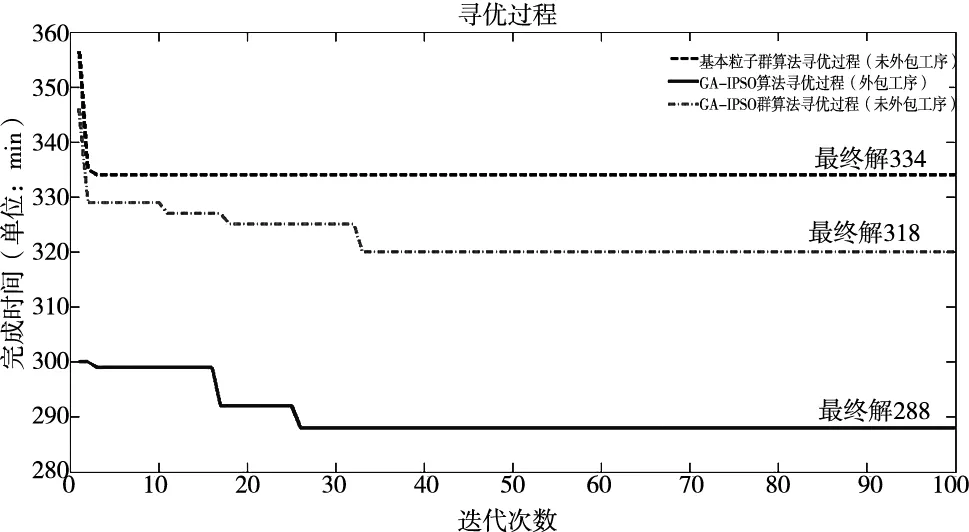
图4 迭代对比图

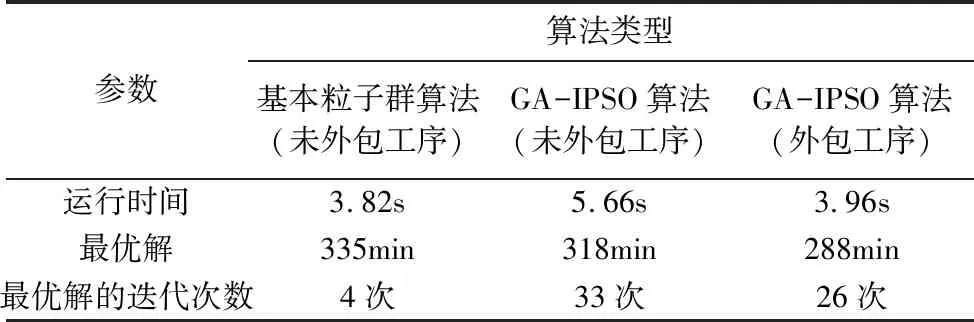
参数算法类型基本粒子群算法(未外包工序)GA-IPSO算法(未外包工序)GA-IPSO算法(外包工序)运行时间3.82s5.66s3.96s最优解335min318min288min最优解的迭代次数4次33次26次

由3种算法的迭代图以及实验结果对比表可知，基本粒子群算法的运行时间较短且在第4代便搜索出最优解，明显出现陷入局部最优的情况，导致寻优精度较差。而GA-IPSO的执行时间虽较长，但其在迭代进化的过程中有效的避免了进入局部最优，提高了算法的求解精度，使算法更好地趋近全局最优解。在未外包工序时，遗传—粒子群算法求解得到的订单总完成时间为318min，仅比订单要求时间提前两分钟。但在实际操作过程中，如机器操作问题等突发状况会导致实际生产时间不如排程结果精确从而导致订单无法按时交付。因而，排程优化结果并不足以完成要求。

现将6号零件的第3～6道工序安排至其他企业的租赁机器进行生产。其中，租赁机器无生产准备时间，生产所需原材料的运输时间及零件完成后运输回企业的运输时间均为76min。将数据代入排程优化模型并求解得到最优工序排程甘特图及最小完工时间。图5、图6为排程结果调度甘特图。表4为未外包工序与外包工序情况下的排程结果对比表。

图5 GA-IPSO算法的调度甘特图(未外包工序)

图6 GA-IPSO算法的调度甘特图(外包工序)

参数排程类型未外包工序外包工序生产完工时间318min288min机器等待时间249min224min

实验结果表明：加入了遗传算法部分功能后的GA-IPSO算法能够极大地降低算法在求解过程中进入局部最优的概率，有效提高了算法的求解精度。并且租赁其他企业的生产机器时，通过高级计划排程模型进行生产线排程，可得到最小完工时间为288min，生产过程中各机器的空闲时间为224min，明显少于未租赁机器时的排程结果。租赁其他厂的生产线能够极大减少零件制造时间，降低生产过程中各台机器的等待时间，压缩了生产成本，有效地提升了企业的生产效率。