基于DVL信息辅助下的捷联惯导初始对准可观测性分析∗

罗银波 张光俊 胡柏青 常路宾

（1.海军驻九江地区军事代表室 九江 332000）（2.海军工程大学导航工程系 武汉 430000）

1 引言

目前的水下导航技术使以前被认为不可能或不切实际的新兴应用成为可能，包括自主海军作战，海洋学研究和冰下调查。尽管取得了重大进展，但精确导航仍然是对所有水下平台的重大挑战［1～2］全球定位系统（GPS）为水面以上的车辆提供卓越的三维导航功能，但由于GPS射频信号的水堵，不能在水下。这限制了GPS用于测量声学转发器或帮助水下应用的传感器校准［2］。声学导航广泛用于有限区域的科学和工业水下航行器，其需要事先小心地将信标固定或停泊在海床上或水面舰艇的船体上。

多波束多普勒计程仪（Doppler Velocity Log，DVL）可以提供海底跟踪或水层跟踪3-D速度。计程仪的测量值是绝对速度，而且测量值中不含有随时间积累的误差［3～4］。当IMU测量任意三维（3D）角速度和平移加速度时，IMU可以测量任意三维（3D）角速度和平移加速度，从而产生导航信息。使用IMU进行DVL联合可以在未开发区域进行大规模水下导航。它们在特征上相互补充。DVL速度有助于IMU减轻累积的导航误差和校准惯性传感器误差。另一方面，IMU的短时稳定性有助于DVL自适应地更新由于水温和密度等环境因素而可能发生显著变化的参数［5～6］。

在利用DVL与SINS进行初始对准时，一般将系统误差及相关器件的误差作为状态变量进行滤波估计，状态估计的精度及速度决定着系统初始对准的速度及精度，而状态估计的精度及速度又与系统的可观测性有很大关系，当被估计的状态不可观测或者可观测性较低时，将状态估计值反馈给系统会造成系统的精度下降甚至发散，因此需要对系统状态变量进行可观测性及可观测度的分析，常用的可观测分析方法有三种：第一种是1992年Goshen-Meskin和Bar-Itzhack等提出的分段线性定常系统（简称 PWCS）的可观测分析方法［7～9］；第二种是1997年东南大学提出的基于系统可观测矩阵奇异值分解（SVD）的方法［10～12］；第三种是Ham提出的利用卡尔曼滤波器的估计误差协方差矩阵的特征值和特征向量来分析的可观测性分析方法［13］。第一种方法只能分析SINS是否能完全被观测，对于不能完全被观测的系统不能定量进行分析由于SINS属于线性时变系统，判断其是否可观测性比较复杂，不能简单通过秩来判断；第三种方法是在Kalman滤波之后才能进行分析，计算量大，可观测分析复杂；而第二种方法能弥补第一种方法的不足，对于不完全可观的系统能定量分析其可观测度，且计算简单，能将可观测性分析的结果直观地呈现出来。本文首先对PWCS理论及SVD理论进行了介绍，进而构建了基于DVL信息辅助下SINS初始对准的系统模型，最后利于基于系统可观测矩阵奇异值分解（SVD）的方法分别对模型在静止和转动状态下进行可观测性分析，结果表明转动状态下能激励惯性器件的各误差参数，使基于DVL信息辅助下SINS初始对准的系统模型可观测。

2 PWCS理论

对于基于DVL速度辅助的捷联惯导初始对准，载体在每个位置时都可视为线性定常系统，当载体姿态发生变化之后，系统进入另一个线性定常系统，因此整个对准过程可视为分段线性定常系统。因此可以利用PWCS对整个对准过程进行可观测性分析。

PWCS系统有如下模型：

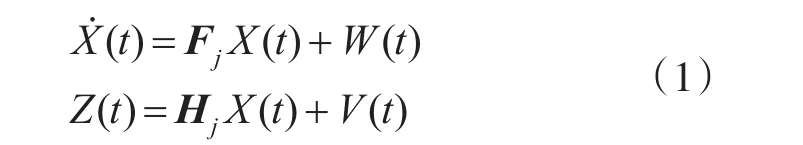
其中，j=1，2，…，r，在第 j时间段内，Fj，Hj为定常阵。

由于捷联惯导系统参数的可观测性与激励无关，为简化分析问题，只研究齐次系统的可观测性。离散化后的齐次方程为

第 j时间段内的观测值可以表示为

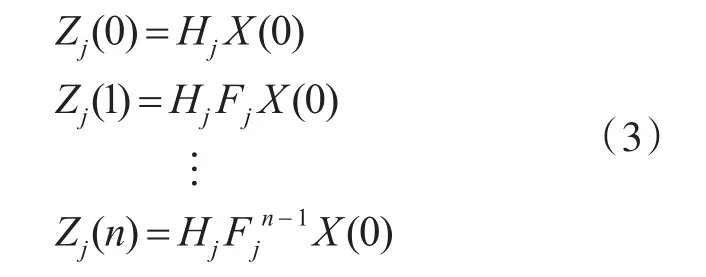
对于第 j时间段内的可观测矩阵可表示为

对于第 j时间段内的观测方程可表示为

则系统总的观测方程可表示为

系统的总观测矩阵（Total Observability Martrix，TOM）为

定义系统的SOM（Stripped Observability Martrix）为

定 理 1：如 果 FjX=X ，∀x∈NULL(Qj)，1≤j≤r，则 NULL{Q(r)}=NULL{Qs(r)}，Rank{Q(r)}=Rank{Qs(r)}。

从定理1可以看出，用SOM代替TOM对系统进行可观测性分析可大大降低系统的维数，降低计算量。

定理2：当且仅当Rank{Q(r)}=n时，系统是完全可观的。

3 基于SVD的可观测度分析方法

基于PWCS理论的可观测分析方法只能判断系统是否完全可观测，对于不完全可观测的系统，PWCS方法不能定量的分析。而基于SVD的可观测性分析方法则能定量的分析状态变量的可观测度。

设系统的可观测矩阵为Q，观测序列为Z，初始状态为 X0，则

根据矩阵理论中奇异值分解的方法，将Q分解如下：

将式（11）代入观测方程中有

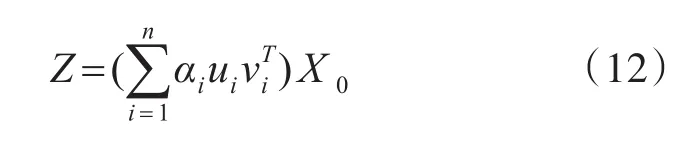
如果 αn＞0，则

当αr=αr+1=αr+2=…=αn=0时，

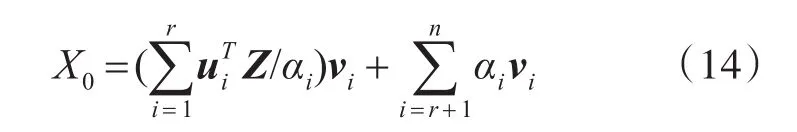
其中αi是该系统零空间中任意系数，该系数有很多可能的解，因此不能用观测量将初始状态估计出来。

当Z具有常值范数时，X0的上界为

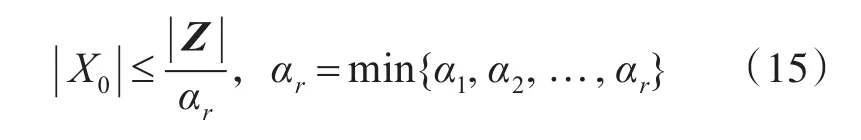
式（15）说明，奇异值越大，X0的上界越小，则状态变量的估计性越强。

综合PWCS理论和基于SVD的可观测性分析方法，总结出求系统各个状态变量的可观测度的方法，步骤如下：

1）从第一个时间段开始，令 j=1；

4）计算该时间段对应的外观测量Z的值；

5）根据每一个奇异值 αi与对应的 ui，vi，计算对应的状态变量X(0)，并根据X(0)的值判断各个状态变量的可观测度；

6）按照上述步骤继续分析下一段时间段，直至最后一个时间段为止。

4 基于DVL速度信息辅助的SINS初始对准系统模型

基于DVL速度信息辅助SINS在系泊条件下进行初始对准时，可直接利用载体系速度信息作为观测，利用DVL提供的载体系速度和惯导解算的导航系速度之间的姿态转移关系构造量测方程。考虑到陀螺刻度系数误差[δKG]、加速度计刻度系数误差[δ KA]、陀螺安装误差[δ G ]、加速度计安装误差[δA]、里程计刻度系数误差δKD其在系泊条件下的观测模型可表示为

1）速度误差方程

取“东北天”坐标系为导航坐标系，在系泊条件下VN=VE=0，则有

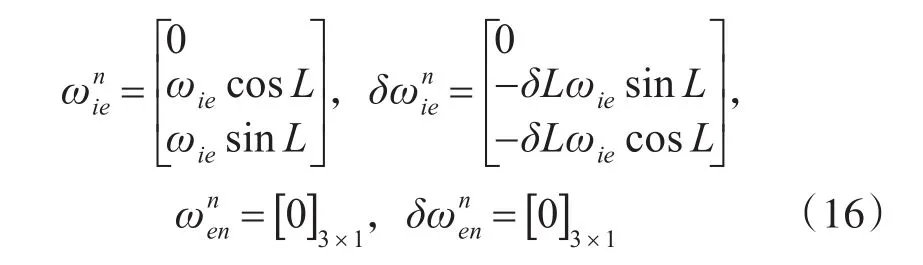
记

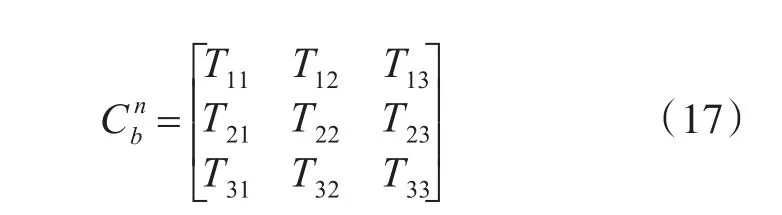
可得到系泊条件下以分量形式表示的速度误差方程为

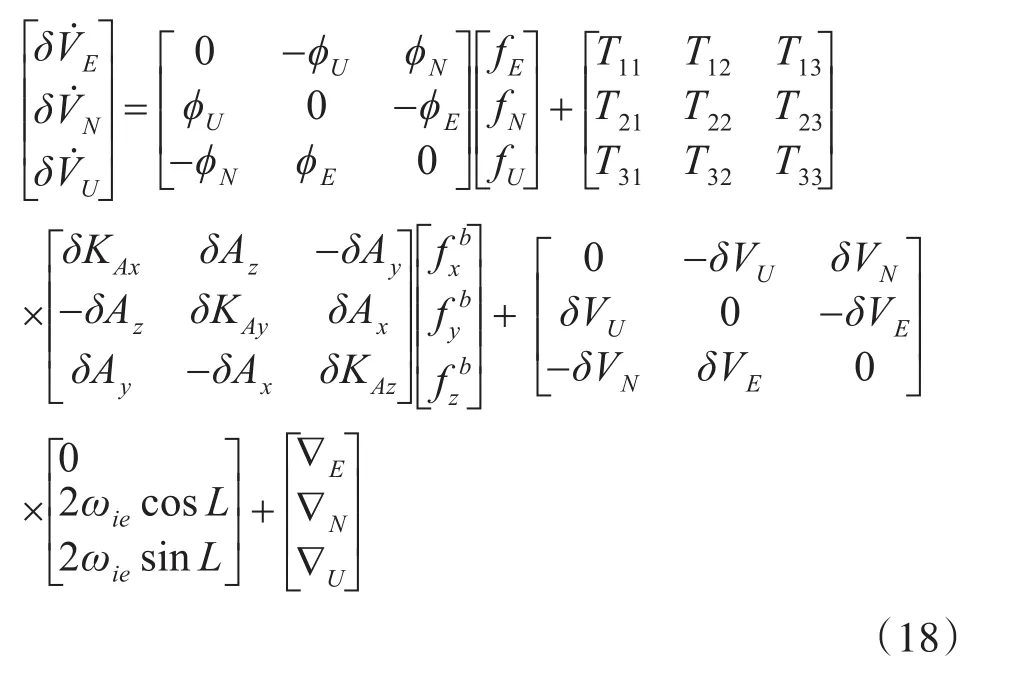
其中

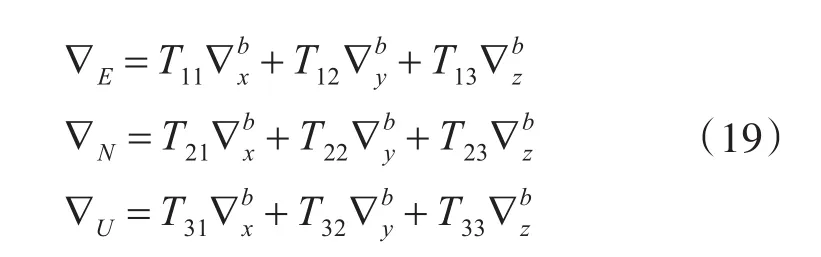
2）姿态误差方程

取“东北天”坐标系为导航坐标系，得到系泊条件下以分量形式表示的姿态误差方程为

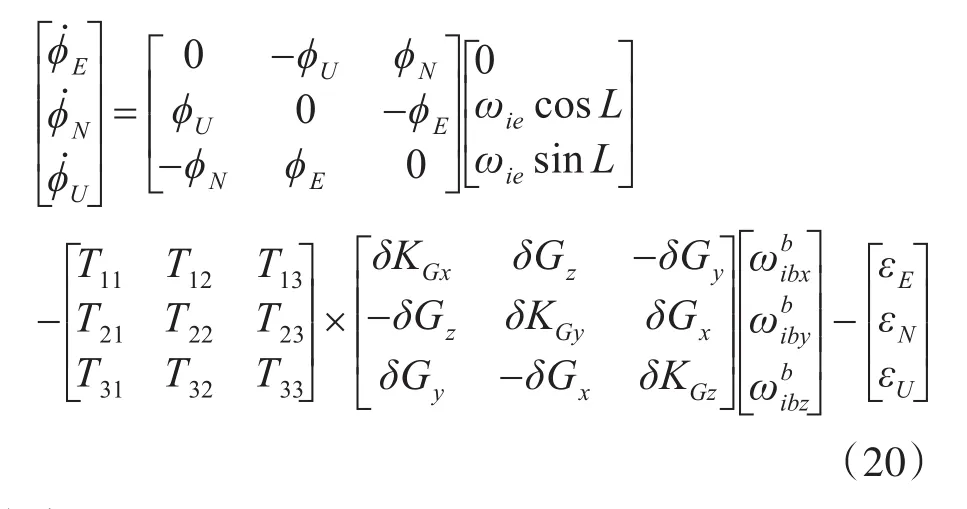
式中

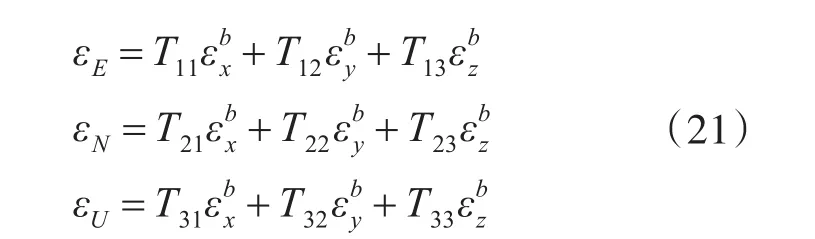
在系泊条件下，解算得到的位置和速度即为速度误差和位置误差，陀螺仪和加速度计的各项误差参数通过误差传递影响导航输出，即解算得到的导航误差中包含了上述误差源。系统状态方程为

其中X包含25维变量，形式如下：

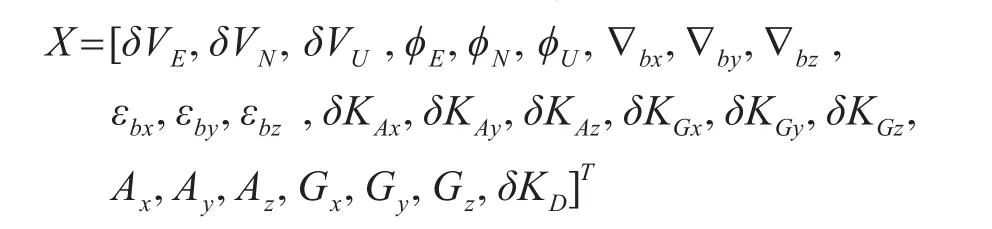
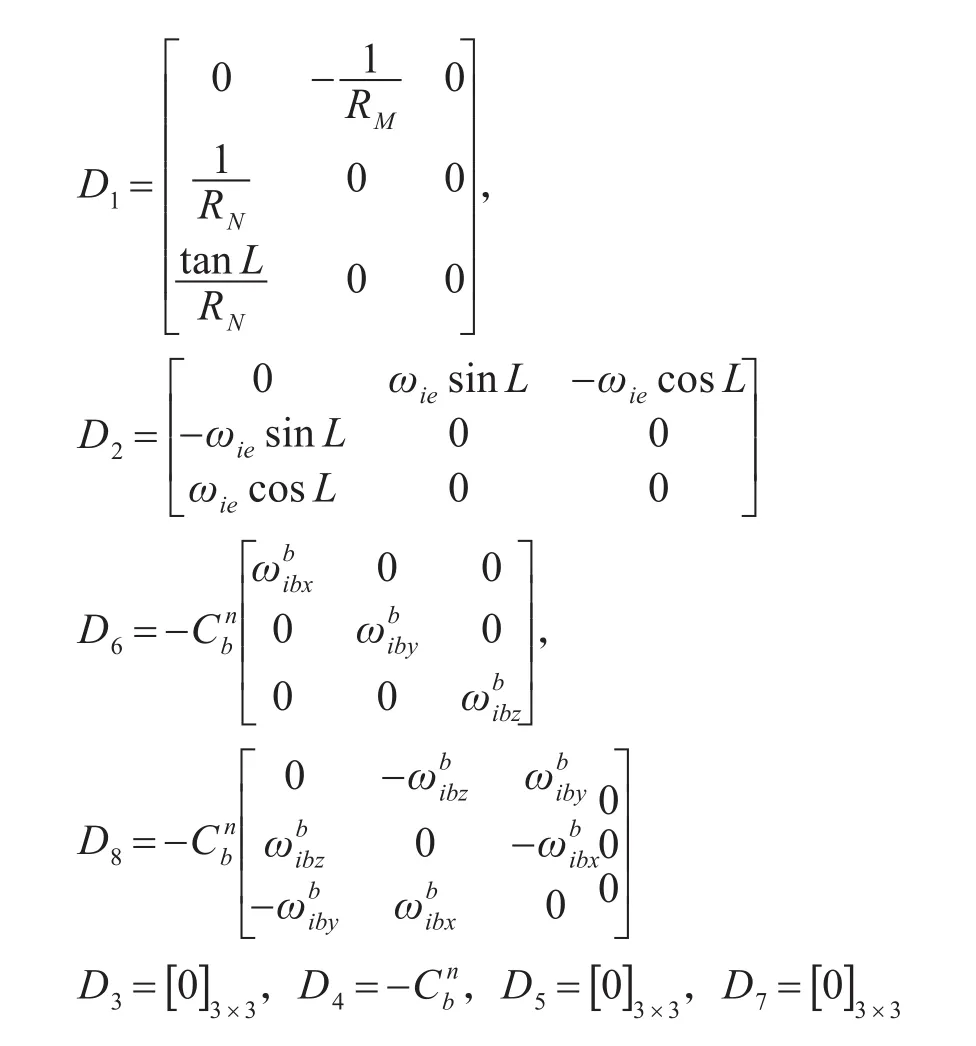
F为状态转移矩阵，根据上一节推导的误差传播模型，状态转移矩阵F具有如下形式：

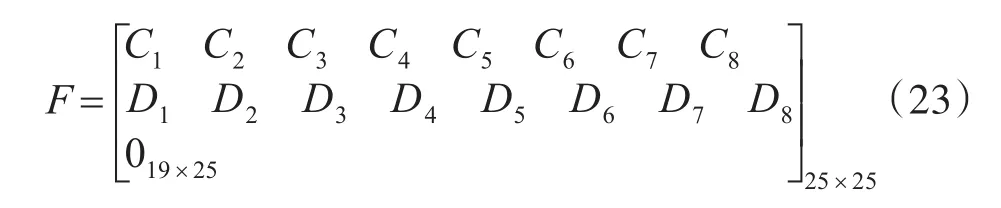
其中

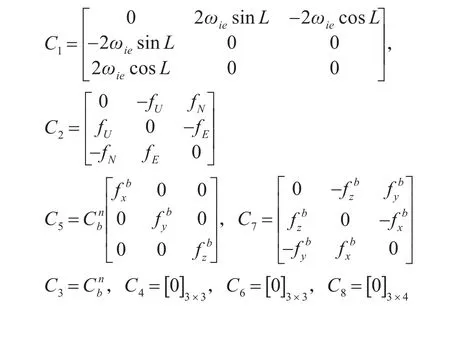
观测方程为

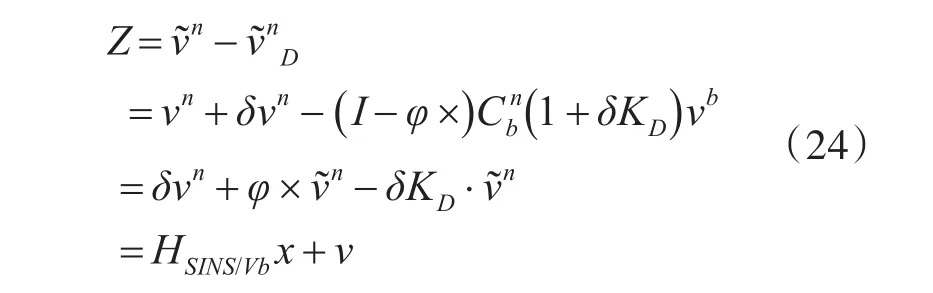
其中，观测量 Z=[δVE，δVN，δVU]T，观测矩阵 H 为

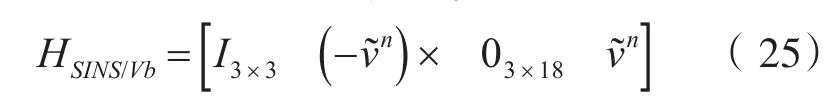
将式（23）和式（25）描述的系统进行离散化：

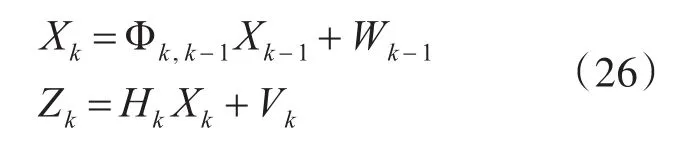
上式中，Φk，k-1为一步转移矩阵，Wk为系统激励白噪声，Vk为量测白噪声。同时Wk和Vk满足：

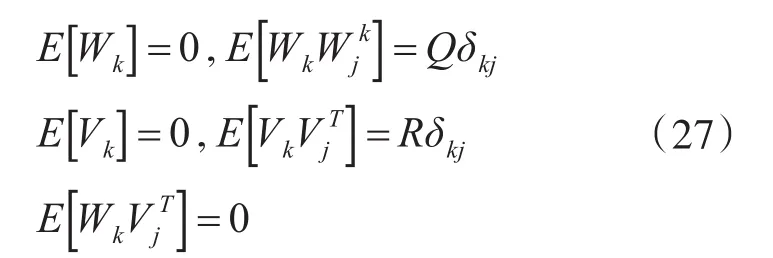
5 可观测性分析实验

在不同激励条件下，基于DVL的捷联惯导初始对准模型各误差参数的可观测性是不同的，只有可观测的误差参数才能通过卡尔曼滤波进行估计，此处考虑载体静止及转动的情形，其运动分段情况如表1所示。

表1 分段转动的每阶段情况

限于文章篇幅，仅并列出相应的可观测状态变量的奇异值表格。

1）当载体处于静止时，捷联惯导系统指向：东、北、天，陀螺仪和加速度计敏感到的信号以及载体的姿态矩阵分别为

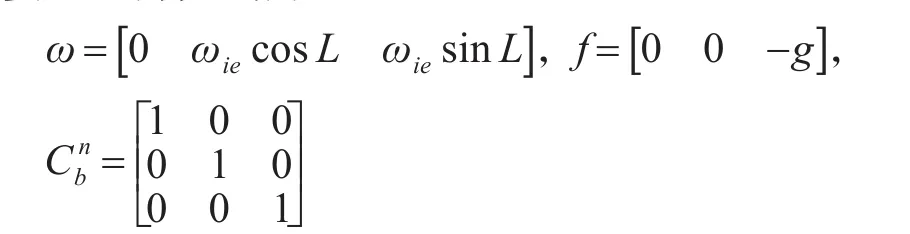
利用SVD分解得到静止状态下各个状态量的可观测度如表2。

表2 位置1可观测性

由上表可以看出，当载体处于静止状态下时，水平加速度计零偏、方位陀螺仪漂移均处于不可观测的状态，因此需要将全部的误差参数激励出来，必须依靠载体转动来完成。

2）当载体从位置2旋转至位置3时，起始时刻陀螺仪和加速度计敏感到的信号以及载体的姿态矩阵为

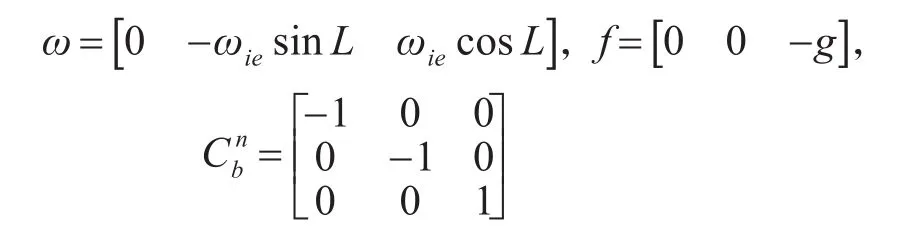
由直方图分析载体在由位置2转至位置3的过程中可观测的状态变量及其奇异值如表3所示。

由表3明显看出，当载体从位置2转到位置3时，加速度计的两个水平零偏和水平安装误差可观测，陀螺仪的零漂和Y轴上的安装误差可观测，另外，水平姿态角及速度误差也是可观测的。将载体转动时的可观测情况与静止时比较，证明载体转动时能激励惯性器件的各误差参数，使其可观测。

表3 位置2转动至位置3可观测性

6 结语

本文首先对PWCS理论及SVD理论进行了介绍，进而构建了基于DVL信息辅助下SINS初始对准的系统模型，最后利于基于系统可观测矩阵奇异值分解（SVD）的方法分别对模型在静止和转动状态下进行可观测性分析，结果表明转动状态下能激励惯性器件的各误差参数，使基于DVL信息辅助下SINS初始对准的系统模型可观测。