局部最优分箱及其在评分卡模型中的应用

夏晨琦

（北京中关村融汇金融信息服务有限公司，北京 100089）

0 引言

信用评分卡类型众多，从客户业务周期角度出发有申请、行为评分卡，从产品对象角度有风险、收益、流失评分卡等，各评分卡既有相同的基础指标，又有自身的特色变量，其目标变量各不相同。各变量数据的探索、采集、加工、衍生是建模的基础和关键，特别地，一个优秀的自变量往往能够大幅提高模型效率。大数据时代，在数据处理及计算机运算能力卓越的基础之上，现代评分卡建模前往往预收集成百上千的变量。

针对不同的变量类型，传统的变量能力评测方法是对原始变量进行t检验（连续性变量）、F检验、卡方检验（分类变量）、列联表分析、相关系数（Pearson,Spearman）等。由于逻辑回归对变量数据质量的要求高（数据无缺失，异常值对建模的最终结果影响程度大等），连续性自变量的预测能力往往无法从原始数据中充分体现。为此，对原始数据进行转化后，提高建模稳定性，挖掘变量“隐藏”的预测能力成为了现代评分卡模型优化的常用方法，其中，以分箱（分段）方法最为普遍及有效。

1 模型评价方法

对于有监督模型（分类器，包括评分卡），主要评价方法有ROC曲线、LIFT（提升度）曲线或LORENZ曲线（捕获率）等。

1.1 ROC曲线

以ROC曲线评价方法为例，首先引入混淆矩阵的概念（见图1）。

其中：TP代表真阳性数，即预测为阳性，真实值也为阳性的样本数；FP代表假阳性数，即预测为阳性，真实值则为阴性的样本数；TN代表真阴性数，即预测为阴性，真实值也为阴性的样本数；FN代表假阴性数，即预测为阴性，真实值则为阳性的样本数。

因此，TP/P（真阳性数/样本阳性数）代表捕获率（或称召回率、灵敏度），TN/N（真阴性数/样本阴性数）则为真负率（或称特异度）。

图1 混淆矩阵

按预测概率对样本排序后选取临界百分位点（一般选取等距间隔，且间隔越小，曲线越平滑），根据每个百分位点可得到n组TP/P（TPR）和(1-TN/N)（1-TNR），将这些值对应的点连接起来，就构成了ROC曲线,而曲线下的面积AUC（Area Under Curve,范围为[0.5,1））便成为评价模型的一种标准（越大越好）。

1.2 LIFT曲线

许多业务场景往往关注模型的响应率，此时ROC曲线（捕获率）不再是模型评价的核心，而另一种方法LIFT曲线能更清晰地展现模型的命中能力：

提升度即模型在选定深度（百分位）的命中率与基线概率（也称先验概率，即样本概率）的比值。LIFT越高表明模型对原始概率的优化提升能力越强。例如，在风险识别的业务场景中，样本原始不良率为5%。现定义深度为10%，即取预测概率排名前10%的样本，其不良率上升至30%，则不良样本命中率提升至原先的6倍（LIFT=6），提高了风险识别能力。

1.3 带惩罚的评价指标

在逻辑回归模型中，可以使用AIC、SC等准则统计量来判断方程的拟合优度，且均考虑了模型复杂度的惩罚。设回归模型的极大似然函数为L，值越大，拟合度越好。AIC、SC公式分别如下：

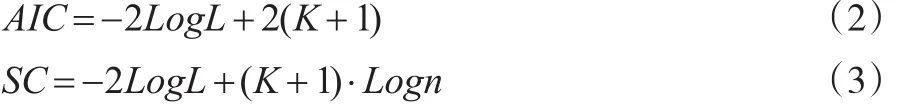
其中，K是自变量的个数，n是样本数量。模型越复杂，K值越大，即“惩罚”越大。AIC、SC的评价标准为其值越小（可为负数），模型越优，因此“惩罚”迫使模型降低变量数。

1.4 K-S检验

K-S检验主要检验两个样本分布是否存在显著差异，在对二元分类模型进行评价时，测算各累计分组（按模型得分进行排序）中正负样本在总体正负样本中各自占比的差异（分布的百分位点是否存在差异），由此评价模型对正负样本的分离程度。

2 分箱方法

分箱技术自诞生以来，形成了许多经典方法，大致可以分为无监督的分箱算法和有监督的分箱算法，前者更易处理，但未提炼目标变量与解释变量的关联性信息。

2.1 无监督分箱

（1）等深分箱

将样本根据指定变量进行排序，并按照样本个数等分成n组，每组数据的指标上下界作为之后指标分段的依据。

（2）等宽分箱

将变量的取值间距等分，使得每个箱体的区间距离相同，但箱体的样本个数可能各不相同。

（3）聚类分箱

基于k均值聚类的分箱，首先确定分箱的数量K，然后根据K均值聚类法将观测值聚为K类。

2.2 有监督分箱

（1）最小熵分箱

有监督分箱方法均要考虑目标变量的取值。

箱中的类别越纯净，熵值则越小，若因变量只有一个水平，则熵值等于0。

令wi表示第i个分箱的观测数占比；那么总熵值为：

最小熵分箱能够最大限度地区分因变量的各类别，即分箱具有良好的区分能力。

（2）最小GINI分箱

类似地，用GINI不纯度替换熵值，同样可以进行最优分箱。此时，再次令表示第l个分箱内因变量取值为j的比例，GINI不纯度为：

GINI不纯度越小，分箱效果越好。

综上，最小熵分箱及最小GINI分箱均属于决策树分箱的方法类，存在过度分箱的问题，即最优化指标值会使得分箱太依赖于目标变量值，导致分箱不平滑或是箱数过多。

（3）BEST K-S分箱

K-S检验除应用于模型外，还可直接对变量进行分箱。将单变量作为一个特殊的二分类模型：

①K-S检验给出区分度最大的区间临界值，并将数据左右分割；

②对于分为两类的样本数据，重复K-S检验对数据进行分割，以此类推。

与最小熵、最小GINI系数分箱相同，BEST K-S分箱同样属于全局最优分箱，但其具有计算成本低，易于调控分裂数，稳定性较强等特点。

3 变量筛选方法

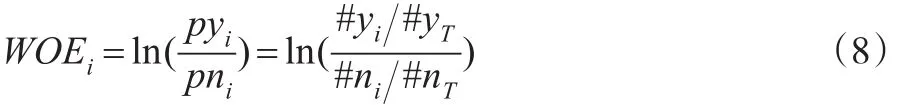
实际上WOE与K-S的思想非常类似，都是对正负样本进行分布差异的检验，其区别在于K-S的取值范围是0-1，而WOE进行了对数转换使得取值范围扩大为(-∞，+∞ )。IV值的公式如下：

3.1 变量自身解释能力

信息值（IV值）全称“Information Value”，顾名思义是对变量的解释信息的提取，IV值越大，表明变量包含的信息越多，对于建模越重要。IV值由WOE值进行加权求和，其中，WOE（Weight of Evidence）表示自变量取某个值的时候对违约比率的一种影响，公式如下：

3.2 变量降维

变量降维是剔除“重复”变量的过程，“重复”指的是变量间的信息包含重合度，即变量间的相关性。对两个变量进行相关性检验，若变量间相关性强，则保留对模型更重要的变量（一般用IV值的大小评判变量对模型的作用）。对于两个连续变量，可计算其Pearson相关系数；若存在一个变量为离散型变量，可采用Spearman相关系数；但对于成百上千的变量，进行两两比较往往花费大量时间。

变量聚类是高维变量批量筛选的首选方法，基本思想是将变量的相关系数矩阵进行因子旋转，得到涉及变量互不相同的主成分，后对第二特征值大于给定阀值的变量类进行分解。聚类后的每组变量中均有最好的代表变量，评判标准为(1-R2)比：

4 局部最优分箱及变量筛选

4.1 局部分箱算法

局部分箱思想基于Best K-S分箱，将Best K-S分箱的全局性拓展为局部性。

（1）Response加权分箱

Response加权分箱是将响应率（准确率）考虑进分箱的算法中，考虑如下虚拟数据（见表1）。

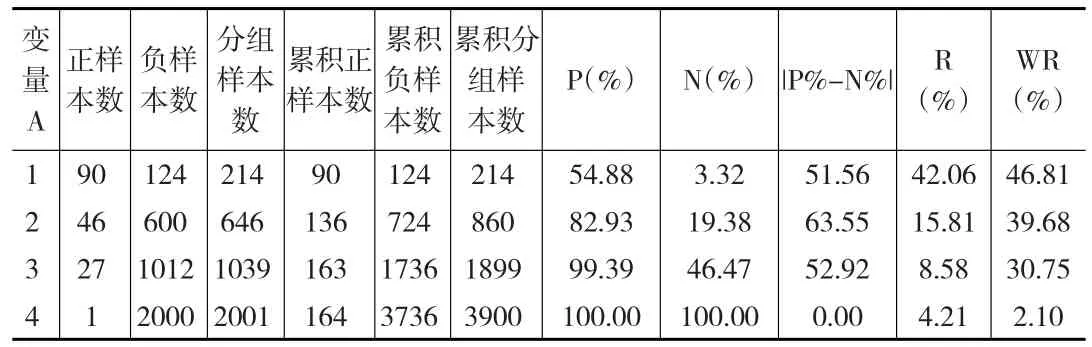
表1 切分点比较

其中，P%代表正样本分布，N%代表负样本分布，|P%-N%|即区分度，Response代表响应率（准确率）。以一次分裂为例，通过Best K-S分箱，易知切分点为2，该水平下样本数据达到K-S值63.55%，然而其Response仅为15.81%，较变量水平＜=1时（42.06%）下降了60%以上的准确率，这与区分度的提升幅度（23.25%）形成较大的差异，因此，若从切分点为1转换至切分点为2，变量的解释效用呈现衰减特征。

引进创新加权变量，将区分度与响应率进行加权综合考虑，如表1所示，将两者的权重定为50%，相加后的得分最大值（46.81%）指向了切分水平1，虽然在全局上未形成最大的区分度，但在局部（前10%）的数据中得到了最优切分。

不同的数据对权重的敏感性较强，因此较优的分箱方式是对权重进行遍历。考虑更新虚拟数据（见表2）。

当变量水平＜=1时，Response达到了100%，但此时正样本数为1，负样本数为0，该水平下样本本身不具规模，Response没有代表性。将Response权重从50%降至40%，同样得到了局部优化。算法实现：

第一步：对连续型变量水平进行从小到大排序，分别计算向上及向下累积正样本量、累积负样本量、累积分组样本量，从自变量与目标变量概率的正负相关性考虑其解释能力。

第二步：用加权（权重可调整）Response最高分对应的变量水平值作为分裂点将样本分为左右两部分。

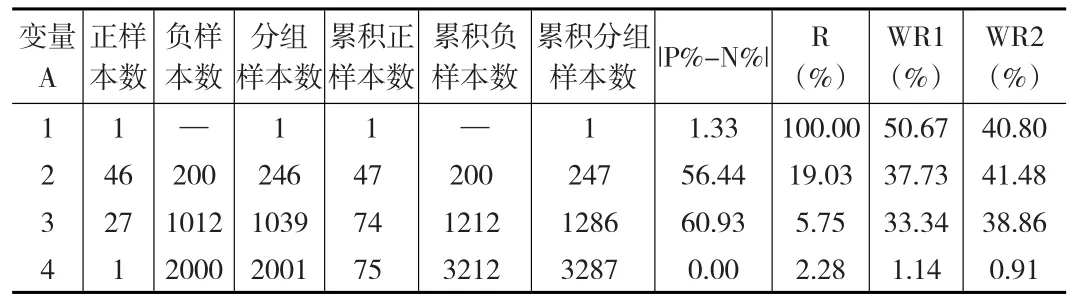
表2 切分点比较

第三步：对左右两部分样本重复第一步和第二步后停止，即一般将变量分为4个箱。

（2）K-S领域分箱

该分箱方法与上文相似，对变量的累计区分度和响应率进行交互作用，但此处不使用加权求和的方法，而是通过查询接近K-S范围的区分度领域中的累积提升度（当响应率不低于基线概率时，提升度=响应率/基线概率；反之，提升度=基线概率/响应率（当响应率=0时，提升度取空值））进行评价，寻找分裂点。算法实现：

第一步：同上文。

第二步：计算变量的K-S值（即区分度最大的值），记为ks。

第三步：计算在区分度＞=α×ks（其中α为扰动参数，设置范围一般为0.95～0.99）时，最大提升度对应的变量水平值，作为分裂点将样本分为左右两部分。

第四步：对左右两部分样本重复第一步至第三步后停止。

（3）召回设限下的最优Response分箱

与Response加权分箱的思想有所不同，不考虑区分度，而对正样本的召回率设定下限，以此保证分裂后的数据具有规模代表性，后以最优Response点进行分裂。

同样以上文中案例为例，如果设定召回率P（%）下限为30%，则其结果与Response加权分箱一致。

该方法的难点在于召回率下限设定：取值过大往往造成对优秀响应率的忽视（如样本在25%召回率时达到40%响应率，但30%召回率或更大时其响应率衰减至10%以下）；取值过小使得变量不能完全发挥效用（如样本在20%召回率时达到60%响应率，但在50%召回率时其响应率也能维持在50%）。为此，采用两维搜索法（见图2）。

图2 Response搜索

按图2箭头方向搜索，若同时满足召回率及响应率，则寻找最优的Response，其中每个参数都可以进行设置算法实现：

第一步：同上文。

第二步：用上述两维搜索法分裂样本。

第三步：不再对满足两维条件的数据集进行分裂，而对剩余一边数据进行第二步，以此类推。

该算法存在复杂度较高，运行时间成本大，低自动化等劣势。

（4）BEST IVi分箱

根据IV值的思想，对累积分组进行WOE与IVi值的计算，搜索使得IVi最大的水平值作为分裂点。

因WOE值是区分度的对数化，其值比RESPONSE值对极端情况更为敏感，所以BEST IVi分箱同样存在结构不平衡的问题。

（5）其他分箱

关于局部最优解思想的分箱层出不穷，可以增加加权的维度，搜索区分度下降速度等，有些遍历方法甚至可以展开探索，本文不再一一列举。

（6）边界调优

原始分箱后，得到的边界值往往不具备业务意义或业务部署效果解读性较差（如边界值为49.67，模型部署时调优至50为宜），因此，分箱后需对原始分箱边界进行调优，即有效位数的保留，使得分段数值更具业务解读性。遍历所有有效数，并保留3位有效数字，末位为0或5。

4.2 变量筛选

在对变量进行分箱以发挥效用后，得到IV值作为对变量的最优评价。变量筛选时，首先剔除IV值过小（一般认为＜=0.02）的变量，然后进行变量聚类。

当变量数成百上千时，直接聚类会降低每类中变量相关性的解释能力。一般地，可以对变量进行人工的初分组，将基于初始变量的衍生变量分为一组，对每组变量进行聚类。

变量聚类可以在变量分箱前完成，这样可以降低变量数，大幅减少建模时间，其缺点是通过变量聚类筛选出的变量虽有最佳的(1-R2)比，而被剔除的变量中可能存在“黄金”变量（IV值高）。因此，本文采用综合评判标准筛选变量，将聚类后每组中变量的IV值和(1-R2)比加权综合，选取综合指标最高的变量。

5 模型实现及分箱对比

本文样本数据来源于KAGGLE网站等互联网现有的或改造后的虚拟数据。

5.1 模型实现

（1）将建模样本分层抽样为训练集（70%）和验证集（30%）；

（2）剔除缺失率超过60%的变量；

（3）对数值型变量进行分箱（分箱方法为BEST K-S分箱及Response加权分箱（权重设为0.2）、K-S领域分箱（α=0.99）等，并进行了取整优化）；

（4）对字符型变量根据水平响应率进行K-MEANS聚类（K=5），从而达到水平降维的效果；

（5）对每个变量进行WOE及IV值的计算，并剔除IV值0.02及以下的变量；

（6）利用综合指标法对变量降维；

（7）变量WOE转码；

（8）逻辑回归建模（backward选择法）；

（9）评分刻度转换；

（10）模型评价。

5.2 分箱对比

以BEST K-S分箱、Response加权分箱、K-S领域分箱模型进行对比（建模其他环节完全一致）：

（1）变量分箱对比

选择某一变量进行对比，结果如表3至表5所示。

表3 Response加权分箱

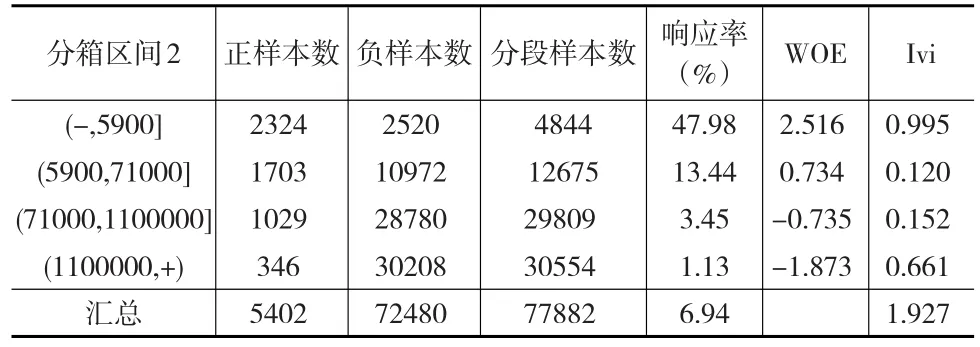
表4 BEST K-S分箱

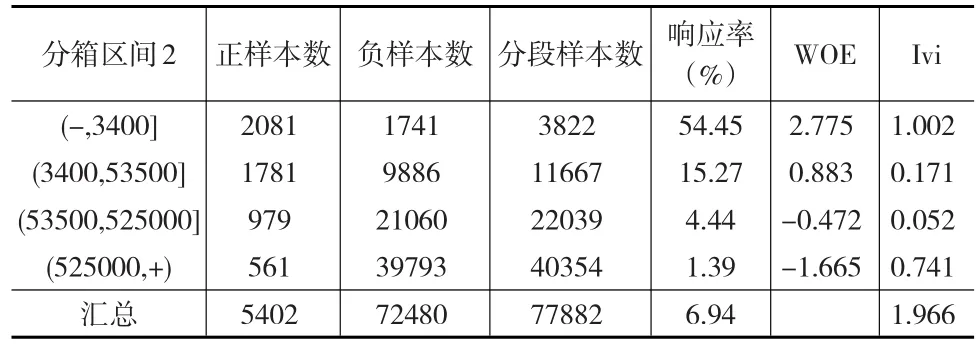
表5 K-S领域分箱

比较上述关于同一变量的三种不同分箱方法，发现Response加权分箱具有最高的IV值，同时其响应率的区分度最为显著；另外，K-S领域分箱在考虑提高区分度的同时，兼顾区间划分的样本规模结构，因此在第一段箱体上得到最高的IVi值，有利于最大效用地发挥变量能力。

（2）模型对比

对基于上述三种分箱方法的建模结果进行比较，情况如下：

①基本指标对比

如表6所示，通过Response加权分箱建模后的指标变量27个，与K-S领域分箱的模型变量相同，而BEST K-S分箱后的模型使用了筛选后的全部变量，模型复杂度较高。

表6 模型效果对比

ROC曲线面积方面，三种模型的差异极小，BEST K-S分箱及K-S领域分箱均为0.911，而Response加权分箱后模型的AUC为0.91，仅降低0.001。

K-S值方面，Response加权分箱后模型表现最佳，为0.6668，其次是K-S领域分箱及BEST K-S分箱模型。

Response加权分箱IV值较BEST K-S分箱高的变量数15个；反之，BEST K-S分箱较Response加权分箱IV值高的变量数有23个，表明权重对每个变量的解析力度不同。

②提升度对比

在SAS环境中分别进行Response加权分箱建模、BEST K-S分箱建模以及K-S领域分箱建模（见表7），并从模型提升度效果的角度出发评价其局部预测能力。根据结果对比发现，K-S领域分箱模型在局部领域的表现最佳，体现了该分箱方法对于头部样本预测能力的提升。

表7 提升度效果对比

6 结束语

基于局部最优思想的分箱方法是对传统全局最优评价的一种补充和创新，除了在Logistic回归方法领域，决策树的分裂规则同样可以利用局部最优的思想进行尝试，特别是衍生至GBDT、随机森林等领域，对于局部最优的集成或许可以得到大幅提升的效果。目前，对局部最优的探索尚处于初级阶段，许多方法和思路有待验证和完善，但显然这种价值挖掘值得长期探索。