基于决策者偏好靶心的混合属性广义灰靶决策方法

马金山

（河南理工大学 能源科学与工程学院，河南 焦作 454000）

0 引言

自灰靶决策方法产生以来，已有诸多学者对其进行了比较系统和深入的研究。混合属性灰靶决策方法则是传统灰靶决策方法的重要改进，它将决策方案的指标值由单纯的实数拓展为既包括实数也包括其他数据类型的混合属性指标值。灰靶决策是依据各决策方案对于靶心的靶心距来评选各方案的优劣。单纯实数型的灰靶决策方法求解靶心距时主要是采用距离法，如通常采用欧氏距离法或具有统计意义的马氏距离法[1,2]。而混合属性灰靶决策方法获取靶心距的手段也在不断地发展：以欧氏距离等为依据的方法最早见诸于文献[3-5]；后来非传统的方法如以蛛网面积和关联系数求靶心距的方法相继产生[6,7]；此外，还有采用以向量为基础的方法[8-10]、以Kullback-Leibler距离为基础的方法[11]获得靶心距，这些称为混合属性广义灰靶决策方法。广义灰靶决策方法是基于灰靶决策方法，在遵循其基本原理不变的基础上提出的一种方法，其基本的计算过程有别于传统方法[8-11]。在广义灰靶决策方法中，以向量为基础的混合属性广义灰靶决策方法，由于所采用的微小向量考虑了不确定数的不确定性信息，且在运算过程中信息的失真较少所以比以距离为基础的方法更优，且相对其他的广义灰靶决策方法在方案排序的稳定性方面更好。

文献[12,13]研究了方案指标值为实数情况下，决策者不同偏好的靶心对决策方案的影响：决策者的正负理想属性偏好所确定的靶心（正或负靶心）均能缩小决策方案指标间的差异，即具有使方案指标聚类的功能。决策者正选择偏好所确定的正靶心对方案指标具有“奖优罚劣”的功能，若方案的其中一些指标值优于正靶心值时，这些指标值视为无差异，均为优秀指标值，相当于对该方案指标的一种“奖励”；当一些指标值劣于正靶心值时，指标之间的差异加大，可视为对该方案指标的“惩罚”。而决策者负选择偏好所确定的负靶心具有对方案指标“奖劣罚优”的功效，即当某些方案的指标值劣于负靶心值时，则这些指标值均被认为是最劣的指标值，相当于是对该方案指标的“奖励”；而当决策方案的指标值优于负靶心值时，则方案指标间的差距变大，实际上反映了对该方案指标的“惩罚”。

已有研究其分析的对象是决策方案的指标为实数值的情形，但在指标为混合属性值且采用以二元联系数向量为计算基础的广义灰靶决策方法时是否具有影响，以及影响的程度如何，是值得研究的。本文给出了基于决策者偏好靶心的混合属性广义灰靶决策方法的原理及步骤，并探讨了决策者偏好靶心对决策方案的影响。

1 基于决策者偏好靶心的混合属性广义灰靶决策方法

1.1 理论基础

定义1：记R为实数域，称x为一个含有不确定性的区间数（包括参数个数多于两个的多参数区间数），则[xL，xU]、[xL，xM，xU]和[xL，xM，xN，xU]分别称为区间数、三参数区间数和四参数区间数，其中参数xL、xM、xN、xU满足0＜xL＜xM＜xN＜xU∈R[14,15]。

定义2：记R为实数域，称A+Bi为二元联系数，其中i∈[-1，1]，A，B∈R，A为确定的项，B为不确定的项，i则是一个变动的项，它统一了不确定数（如区间数和多参数区间数）的确定性和不确定性。

定义3：设xˉ和v分别是x的q（q≥2）个参数的均值和标准差，则：

式（1）为x的q个参数的均值-标准差二元联系数，简称均值-标准差联系数。其中由式（2）和式（3）可得到xˉ和v：

式（2）和式（3）中xˉ可以看作是关于x的q（q≥2）个参数的相对确定性的测度，而v是关于x的q个参数的相对不确定性测度[8]。

定义4：均值-标准差二元联系数u(xˉ，v)中的均值xˉ和标准差v之间的相互作用可以反映到基于集对分析的二维确定-不确定空间（Determinacy-uncertainty，简称D-U空间）中的微小向量，记作 (xˉ，v)[8]。

1.2 决策原理及步骤

1.2.1 所有方案指标值均转化为二元联系数

将不同数据类型的指标值采用式（1）至式（3）统一转换为A+Bi的二元联系数形式，并视其为二维确定-不确定空间中的微小向量。其中实数可视为是二元联系数中的确定项为该数值本身，不确定项为0，即表示为A+0i的形式。设转化后的各指标二元联系数为Ast+Bsti，(s=1，2，…，n;t=1，2，…，m)。

1.2.2 求出各指标属性的靶心指标向量

（1）决策方案靶心的确定

设各方案指标的微小向量为Ust=(Ast，Bst)，(s=1，2，…，n;t=1，2，…，m)，则可以由式（4）确定决策方案各指标属性的靶心。

式（4）表明，对于效益型指标属性的靶心，即求指标向量范数最大对应的指标向量为靶心，而当有几个指标向量的范数相等时，则选择不确定性项小的指标向量作为靶心；成本型指标属性靶心，即求指标向量范数最小对应的指标向量为靶心，当有几个向量的范数相等时，则选择不确定性项小的指标向量作为靶心。

（2）决策者偏好靶心的确定

（3）混合靶心的确定

定义7：设由决策方案各效果测度Ust(s=1，2，…，n，t=1，2，…，m)所确定的靶心为，而决策者对属性的偏好为…，m})，则融入决策者偏好的靶心为，其中则由式（5）得到：

1.2.3 决策方案各指标值的预处理

式（6）中的Ist是预处理后的指标测度，如无特殊说明则一般以二元联系数的形式表示。

1.2.4 决策方案各单指标接近度的求解

定义8：设rst为基准指标向量的模，pst为指标向量(s=1，2，…，n;t=1，2，…，m)在指标向量Yst上的投影，则：

式（7）为投影值pst与基准指标向量Yst的模rst的距离，称为接近度，其中

1.2.5 各属性下单指标接近度的归一化处理

前面所求出的各属性下各指标向量与靶心指标向量的接近度彼此是不同的，各属性之间不具有可比性，因此，需要对各个属性下的单指标接近度dst进行归一化得到zst：

1.2.6 求各决策方案加权的综合接近度

给定各个指标属性的权重wt，则可以获得各个决策方案的综合接近度为：

而根据NEs的值由小到大的顺序进行排序，即可得到各决策方案的优劣。

2 决策者的偏好靶心对决策方案的影响

2.1 基本参数及假设

设在同一属性At下，各指标的二元联系数向量为，并设任意两个指标向量分别为U1=(x1，y1)和U2=(x2，y2)。为简单起见，这里仅对正向指标值进行分析。设在属性At下决策方案确定的靶心指标向量为C0=(x0，y0)，而由决策者偏好所确定的靶心指标向量为Cd=(xd，yd)。在同一属性At下求出Us=(xs，ys)、U1=(x1，y1) 和U2=(x2，y2) 分 别 与C0=(x0，y0) 和Cd=(xd，yd)的接近度，分别设为ds0、dsd、d10、d1d、d20和d2d。

2.2 影响分析

为了分析决策者的偏好靶心对决策方案的影响，这里分别求任意两个指标向量在不同靶心下的归一化接近度的差，得到Δd和ΔD。

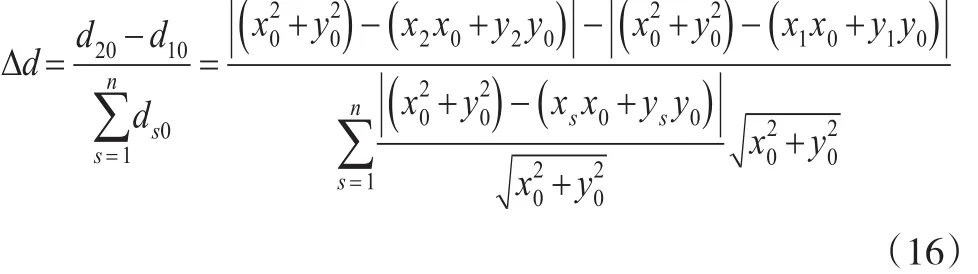
为了分析决策者的偏好靶心对决策方案的影响，则求Δd和ΔD的比值，可以得到：

（1）若决策者的偏好确定的靶心为理想偏好靶心

由于 π1≥1，π2≤1，而，所以不能准确地确定决策者的理想偏好所决定的靶心对决策方案的影响。当时，决策者理想偏好确定的靶心对决策方案无影响；当时，决策者理想偏好确定的靶心使得决策方案之间的差异变小；当时，决策者理想偏好确定的靶心使得决策方案之间的差异变大。

（2）若决策者偏好确定的靶心为选择偏好靶心

由于 π1≤1，π2≥1，所以不能根据 π1和 π2判断与1之间的关系。

由于 π1＜1，π2＞1，因此，不能够准确地判断π1·π2与1之间的关系。

综上，决策者偏好所决定的靶心为理想偏好时对决策方案的影响具有不确定性。当时，决策者选择偏好确定的靶心对决策方案无影响；当时，决策者选择偏好确定的靶心使得决策方案之间的差异变小；当时，决策者选择偏好确定的靶心使得决策方案之间的差异变大。

2.3 决策者偏好靶心对决策方案不确定性影响的原因

由上面的分析可知无论是决策者的理想偏好所决定的靶心还是决策者的选择偏好所决定的靶心在基于向量的混合属性广义灰靶决策方法中对决策方案的影响存在不确定性，可能的原因如下：

（1）该运算方法采用的是不同于以距离为运算基础的二元联系数向量形式，各种不同类型的数据的向量运算使得运算过程存在着不确定性。

（2）不确定数（区间数及多参数区间数）在转化为二元联系数的过程中存在着不确定性，尽管该方法致力于信息丢失的降低。

（3）决策者偏好的靶心和决策方案的靶心之间的关系由于在向量模式下的关系并不明确，为此导致决策方案不确定性的产生。

3 算例分析

3.1 指标与数据

为对煤矿进行综合安全评价，采用的指标包括煤层倾角（°）、煤层瓦斯涌出量(m3/t)、煤矿的平均涌水量（m3/h）、煤的自然发火期（月）、通风设施的合格率（%）、等积孔(m2)、百万吨死亡率（人/106t）以及事故的经济损失（105元），分别用A1—A8表示；共有10个待评价煤矿分别用S1—S10表示。所有指标属性中A1和A2为三参数区间数，A3和A8采用区间数表示，A4、A6和A7用实数表示，而A5则为四参数区间数。矿井综合安全评价数据如表1所示。决策者对属性有偏好，偏好属性分别为A2、A5、A6和A7，偏好值分别为[1,1.2,1.4]、[94,95,96,97]、2.0 和 0.2。其中 A4—A6为效益型指标，其余的为成本型指标。

表1 矿井综合安全评价数据

3.2 决策过程

（1）求各决策方案的灰靶靶心

首先采用式（1）至式（3）将表1中的原始数据统一转化为二元联系数的形式，结果如表2所示。然后运用式（4）求得初始的由决策方案内部所确定的灰靶靶心为Ca=（[6,11,13],[2.8,4,4.3],[100,140],12,[100,100,100,100],3.6,0,[280,320]）。

表2 决策方案指标值的二元联系数形式

（2）求融入决策者属性偏好的灰靶靶心

运用式（5）将决策者的属性偏好融入灰靶靶心后，则可以得到融入决策者属性偏好的灰靶靶心为Ca=（[6,11,13],[1,1.2,1.4],[100,140],12,[94,95,96,97],2.0,0.2,[280,320]）。

（3）基于决策者属性偏好的灰靶靶心C0对决策方案指标值进行预处理

采用式（6），针对原决策方案指标值基于C0进行预处理。

（4）求各决策方案单项指标的接近度

采用式（7）可以求得各决策方案的单项指标接近度。

（5）各决策方案单项指标的接近度归一化

采用式（8）可以得到各单项归一化接近度，见表3。

表3 各单项归一化接近度

（6）综合各归一化单指标靶心距

若专家给出的权重为W=（0.06,0.15,0.03,0.08,0.12,0.13,0.27,0.14），则运用式（9），可以得到各方案的综合靶心距为 w=（0.039622,0.10203,0.148899,0.058519,0.080203,0.01069,0.18638,0.155308，0.130872,0.067476），因此各方案排序的结果是：S6＞S1＞S4＞S10＞S5＞ S2＞S9＞S3＞S8＞S7。而不考虑决策者的属性偏好时，若仍用上述专家给出的各属性权重W=（0.06,0.15,0.03,0.08,0.12,0.13,0.27,0.14），则可以得到各方案的综合靶心距为w=（0.05464,0.094139,0.144376,0.048597,0.088745,0.020213,0.161967,0.169492,0.125855,0.071976），方案排序的结果是：S6＞S4＞S1＞S10＞S5＞S2＞S9＞S3＞S7＞S8。

3.3 分析讨论

下面对上述运算时是否考虑决策者偏好靶心的结果进行比较。其中靶心距与排序变化的比较结果列于表4。

表4 未考虑及考虑决策者属性偏好时方案的变化

从表4可以看出，未考虑决策属性的偏好及考虑决策属性的偏好时，方案的综合靶心距及排序是有变化的。考虑决策者偏好靶心前后，方案除S1、S4、S7和S8略有变化外，其余都没有变化，说明决策者的属性偏好对方案的排序有一定的影响。

4 结论

本文提出了基于决策者偏好靶心的混合属性广义灰靶决策方法的原理及步骤，并分析了偏好靶心对决策方案的影响。决策者偏好所决定的靶心对决策方案虽然有影响，但影响的方向和程度并不容易把握。而决策者偏好所决定的靶心对决策方案的影响难以把握的可能原因是采用了以向量为基础的靶心距处理方法，混合数据在转换及运算过程中存在着信息的不确定性且无法精确衡量。