热激励下碳纳米管与水混合体系传质传热的分子动力学模拟
2019-04-29唐元政蒋英男
唐元政, 刘 增, 何 燕, 蒋英男
(青岛科技大学机电工程学院, 青岛 266061)
1 引 言
沸腾传热是热量传给液体, 使液体沸腾汽化的对流传热过程. 高度过热和急速下的爆发沸腾会表现出特殊的传热效果, 这与在爆发沸腾过程中, 汽相、 液相的升温吸热以及汽化潜热对温度变化的影响有重要的关系[1], 爆发沸腾产生的内应力变化也会改变体系的热导率[2], 爆发沸腾涉及非稳态过程, 时间和空间尺度小, 以及热力密度大, 在实验的基础上很难得出精确的结果, 需要我们在微观条件下探究其分子运动的规律. 目前, 一些真正意义上的微纳米技术已经得到了很大程度的发展, 如纳米尺度下流体流动规律, 微反应控制等研究[3,4]. 此外, 对于强化纳米流体传热特性的研究已经有很多的尝试, Eastman等[5]在基础液里添加体积分数为0.3%的10 nm粒径铜颗粒, 观察到热导率增大了40%. Das等[6]在基础液水中添加1%~3%体积分数的铝纳米颗粒, 观察到热导率增大了25%. He等[7]通过实验研究发现TiO2-H2O纳米流体的对流换热特性在Reynolds数等于1500时增大了12%, 而在Reynolds数等于5900时增大了40%以上. 微纳米尺度的流体相变和流动过程尺度太小, 实验的方法同样很难预测其达到相变平衡的时间. 为了更好的探究爆发沸腾换热和纳米流体传热, 我们采用计算机模拟的方法. 分子动力学可以通过求解粒子的运动方程, 从而研究物质的宏观性质[8], 已经发展成为从原子水平研究物质性能的有效方法. 因此, 可以利用分子动力学的方法研究碳纳米管与水混合体系的传质传热特性. 在之前的研究中,水的爆发沸腾传热和碳纳米管的传热已有较为详细的介绍, 但是把两者结合起来, 研究这一体系传质传热的分子动力学研究还未有详细的文献报道.
2 模型建立
计算模型如图1-1所示, 模拟单元xoy截面是正方形, 整个模拟单元的尺寸为20×20×1000 Å3, 模型在三个维度上均采用周期性边界条件, 填充部分为1 g/m3的水和(5,5)碳纳米管. 共分为2个模型, a是在y等于0到100 Å的范围内充满1 g/m3的水; b是在y等于0到100 Å的范围内加了长100 Å碳纳米管和剩下部分1 g/m3的水模拟过程中, 在80 Å到100 Å的范围内加热.
计算采用LAMMPS[9]软件, 水分子模型采用TIP3P模型[10], 碳原子间的相互作用势采用Tersoff势函数[11], 这一势函数可以很好的模拟碳材料在各种环境下的相互作用. 碳和水分子间以及水分子相互作用均用Lernard-Jones势[12]描述, 具体参数为σc-o=3.19 Å,εc-o=0.3920 kJ/mol, σo-o=3.166 Å, σo-o=0.650 kJ/mol[13], 截断半径为10 Å. 时间步长取1 fs.

图1 纯水(a)、 碳纳米管与水混合体系(b)模型Fig. 1 Pure water (a), carbon nanotube and water mixing system (b) models
3 结果与讨论
本部分模拟分两部分分子动力学过程完成: (1)对图1-1(a)(b)盒子进行NVT控温, 监控不同温度下两种体系的状态, 对不同时刻盒子在z轴方向的密度分布进行统计. (2)对图1-1(a)(b)所示水盒子设置一层厚度为20 Å的高能表面水层(1000 K, 80~100 Å), 设置时间为100 fs, 监控不同时刻体系的状态, 同样对其密度分布进行统计.
控温过程是系统在正则系综(NVT)下进行1000 fs的Nose-Hoover控温, 使系统稳定在300 K; 然后撤掉控温, 在微正则系综(NVE)下进行10 ps计算. 100 fs时刻, 高能表面放热完成, 温度被撤掉, 盒子没有太大变化. 随后1000 fs至100000 fs,盒子内高能表面下的水开始沸腾.
3.1 密度分布
图2-1中和图2-2分别是在初始时刻和100000 fs时刻, 统计得到的模型z坐标方向(分100层,1 nm/层)的密度分布.
图2-1中和图2-2中, 在z坐标方向上表面100 nm处有一个“翘起的尾巴”, 这是前述的由于周期性边界水分子重新进入盒子造成的. 为了便于观察, 对其在z方向前20层(20 nm)内的密度分布统计进行放大, 见插图. 图2-1中, 插图明显可见, 在初始状态0 ps时刻, 水模型稳定在300 K, 上表面位于100 Å处, 说明系统在之前的NVT状态下保持稳定, 且没有沸腾现象. 对比可见, 由于20 Å的高能表面(z方向80~100 Å)的放热作用, 水有明显的沸腾, 在本文模拟的终了状态100000 fs时刻, 沸腾深度大约在3 nm, 上层水最远运动距离在17 nm处, 运动距离7 nm. 图2-2中, 存在碳纳米管情况下, 水的沸腾有加剧的趋势, 沸腾也更加深入和彻底.

图2-1 纯水盒子在z方向密度分布Fig. 2-1 Density distribution in z direction of water model

图2-2 碳纳米管/水盒子在z方向密度布Fig.2-2 Density distribution in z direction of CNT/water model
3.2 温度分布
因为模拟过程中加热的过程极短,而且不是连续加热, 热量的传递会很快, 系统内部温度分布能很好的表现出体系导热性能.
文中的模拟中温度计算是通过以下的方法. 在盒子的分块上z轴分为100份, y轴分为4份, 分成若干个块, 计算每一个块中一组原子的温度得到. 根据下面的公式可以求得每一块的温度
Ke=DOF/(2kT)
式中, Ke是每一块原子的总动能, DOF为这些原子的自由度总数, k是玻尔兹曼常数, T为温度.
图2-3中可以看出, 在z等于18.5处有一个温度极大值, 在z等于3处也有一个温度较高的点, 这说明在较高温度下出现了爆发沸腾的现象, 有较大水团簇来不及蒸发被推到盒子空白的地方, 这是因为受热不均匀所致[14]. 图2-4中该含有碳纳米管的水盒子最终稳定在440 K左右, 比图2-3中温度明显偏高, 而且此刻温度分布沿z方向分布比较平缓, 局域过高的温度几乎没有, 而且整体温度较高, 水沸腾加剧, 这说明了有碳纳米管的存在, 是热传导增加, 有利于沸腾换热和纳米流体传热的进行.
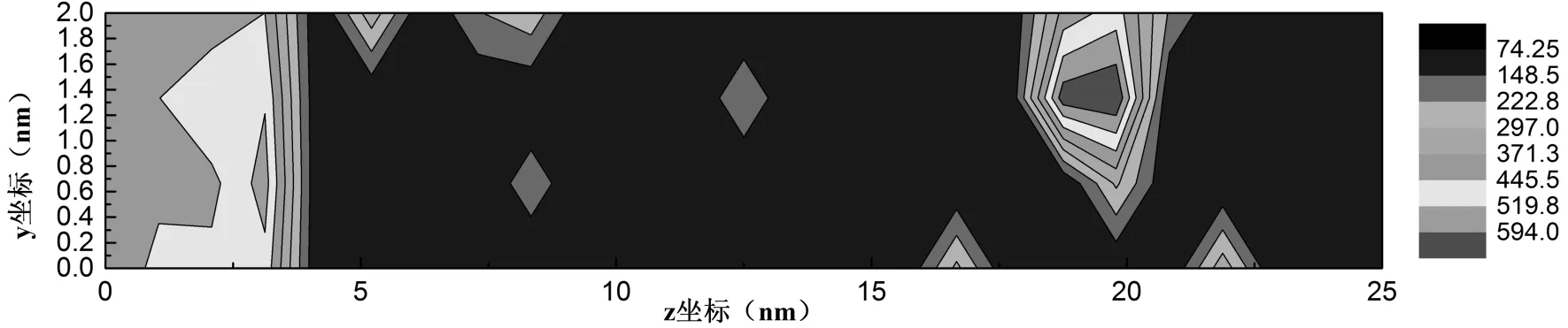
图2-3 纯水盒子在y-z平面上的温度分布Fig.2-3 The temperature on the y-z plane of water model

图2-4 碳纳米管/水盒子在y-z平面上的温度分布Fig. 2-4 The temperature on the y-z plane of CNT/water model
3.3 压力分布
除了上面的温度分布, 这里还计算了体系的应力分布. 应力的计算过程与温度计算过程相似, 分块方式相同, 这里为了方便是先求出一块中每一个原子的应力值然后相加得到总和除以这一区域的体积即可得到这一块中的应力值. 单个原子应力的计算分为六项: 第一项是原子动能的贡献, 第二项是原子与邻近原子俩俩相互作用的贡献, 括角, 二面角和原子之间不正当物的相互作用, 第五项是长程库伦相互作用, 第六项是作用于原子的内部约束力. 当然有些原子不能包括所有项. 根据本文所用的模型和以上应力的分解可以得到本文所说的应力是由于施加了能量之后, 温度发生变化, 各部分之间相互约束而产生应力, 所以根据应力分布可以很清楚的看出能量的分布, 温度梯度的大小, 从而明确热传导的效率.
下面两幅图分别是没有加碳纳米管和加了碳纳米管之后的应力分布图. 这里所说的应力指的是热应力, 根据线性响应理论, 物体受到温度作用时, 质点就要发生位移和相应的应变, 相互约束而产生内应力. 图2-5中可以看出在z等于5、 7.5和16处出现了应力较大的点, 这三个点的温度梯度较大. 另外, 这三个点相对较为集中, 热量只是在这附近没能很好的传播出去, 也说明了此刻水的受热很不均匀, 传热不明显. 由图2-6应力分布可以看出在加热部分出现较大的应力点, 还有就是在很远的地方24和25 nm处有应力较大的点, 其他地方颜色较为单一, 没有较大的温差, 说明了有碳纳米管的存在, 热传导性能得到了很大的提升, 这正是说明了碳纳米管对于爆发沸腾换热和纳米流体传热的促进作用.
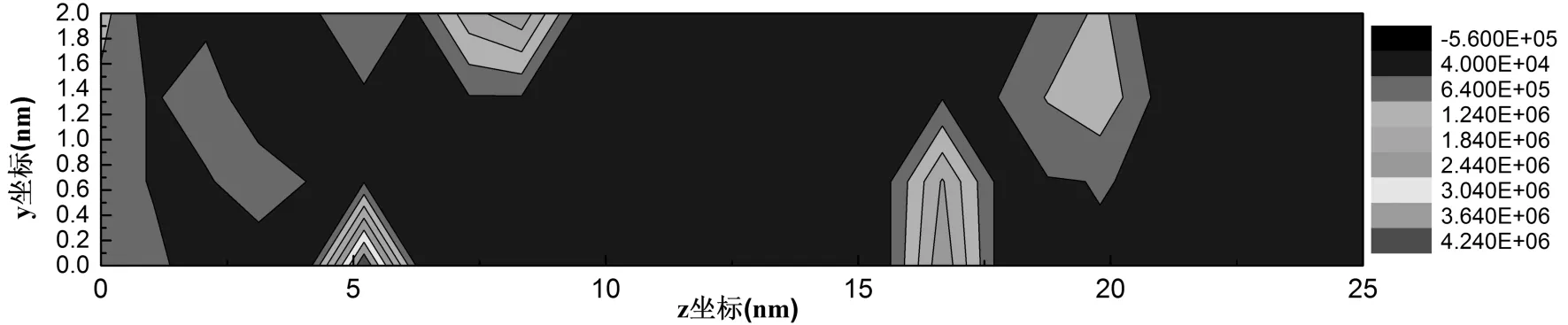
图2-5 纯水盒子在y-z平面上的内应力分布Fig. 2-5 The distribution of internal stress on the y-z plane of water model
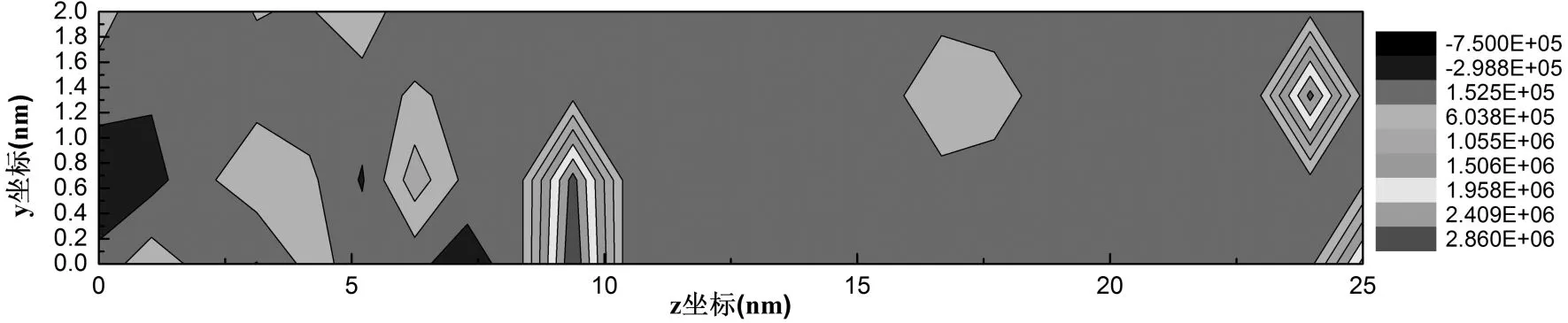
图2-6 碳纳米管/水盒子在y-z平面上的内应力分布Fig. 2-6 The distribution of internal stress on the y-z plane of CNT/water model
4 结 论
沸腾传热的过程较为复杂, 对于热的输送和介质的运动都有较大的关系, 本文采用分子动力学的方法, 建立不同的模型, 分别分析了纯水, 水和碳纳米管同时存在, 较为全面的分析了传热过程中各种因素的影响, 从而得出如下结论.
(1)相比纯水盒子, 含碳纳米管水的模型的沸腾会加剧, 在纯水盒子情况下, 水的沸腾蒸发带走大量热量导致沸腾无法深入进行, 盒子终了温度也不会有较大提高.
(2)而碳纳米管使热量能够迅速、 均匀传播, 加剧了沸腾深度同时提升了终了温度.
(3)碳纳米管具有比较大的热容, 在高温层温度和密度相同情况下, 碳纳米管比水蓄热更多.
