采用灰色Savitzky-Golay滤波的商用车推力杆橡胶球铰非对称迟滞建模

2019-04-29刘巧斌史文库高承明陈志勇闵海涛陈龙

西安交通大学学报 2019年5期

刘巧斌,史文库,高承明,陈志勇,闵海涛,陈龙

(吉林大学汽车仿真与控制国家重点实验室,130022,长春)

橡胶材料是一种优良的隔振材料,而迟滞非线性建模是对橡胶材料的弹性和阻尼等力学特性进行准确而全面表述的有效数学方法。研究橡胶迟滞非线性,对于汽车和机械装置上橡胶件的力学性能,以及减振、抗冲击和降噪等直接影响人的感官评价的性能,乃至可靠耐久性能的预测、优化和控制都具有重要的意义。橡胶悬置、橡胶衬套和推力杆橡胶球铰是汽车上最常用的3种橡胶零件。推力杆作为重型商用车悬架系统的关键导向元件,一般通过衬套式橡胶球铰与车架和车桥相连接,对橡胶球铰的结构、力学性能、疲劳进行深入分析,并通过优化设计提升性能,可为提高车辆的舒适性、平顺性和耐久性提供科学的理论指导,具有重要的工程实用价值。

由于橡胶材料的使用,导致了推力杆纵向力-位移曲线具备了黏弹性非线性材料的迟滞特性。国内外已有大量关于迟滞非线性的研究报道,但对于不同的结构和材料,并不存在一种普遍适用的迟滞非线性模型,需要根据具体情况选取合适的模型。常用的迟滞非线性模型有双线性模型、Bouc-Wen模型、Davidenkov模型、多项式模型等[1],而对于本文所研究的推力杆,其迟滞特性具有非对称特性,直接采用以上方法无法对非对称迟滞特性进行建模,故在对现有对称迟滞模型进行相应改进的基础上,提出可以描述推力杆非对称迟滞特性的模型是本文的一个研究重点。

为获取模型的参数,有必要采用参数识别方法从试验测量的数据中提取有效信息,并在保证模型精度的前提下,最大程度地提高建模效率。由于测试环境的影响、传感器的限制和数据采集记录过程中出现的种种误差,使试验采集到的信号不可避免地包含了噪声信号的干扰,因此对采集到的信号进行有效地滤波是进一步建模和参数识别的基础。常用的时域数据平滑滤波方法有卡尔曼滤波、均值滤波、中值滤波、小波滤波、Savitzky-Golay滤波等[2],而Savitzky-Golay平滑滤波方法具有占用内存小、计算效率高和原理简单等优点,故广泛应用于数据平滑滤波处理领域[3-5]。各种滤波方法在使用时若参数选取不同,则滤波效果存在较大的差异,如滤波不足就不能有效去除信号中的噪声,但滤波过度又会引起信号的失真。因此,提出一个实用的滤波指标,并采用优化方法获取最佳指标下的最优滤波器参数,以提高滤波效果,是本文的另一个研究重点。

当前行业内对于推力杆及橡胶球铰的研究,大多集中于结构有限元分析、刚度模态预测、动静态试验、疲劳分析和优化等方面[6-8],而对其非对称迟滞特性和试验数据滤波处理方面的研究,鲜有文献报道。建立准确高效的推力杆迟滞特性模型是进一步对推力杆进行性能预测、结构优化和整车多体动力学高精度仿真的基础。

本文在进行推力杆纵向迟滞特性试验的基础上,提出了布谷鸟算法优化的灰色Savitzky-Golay滤波方法对试验数据进行去噪,以准确预测去噪后的迟滞特性为目标,分别对线性阻尼模型、分段线性阻尼模型、非对称Bouc-Wen模型和高阶多项式模型的参数进行了识别,通过与试验数据的对比,比较了不同模型的精度和效率。

1 非对称迟滞特性建模

1.1 广义非线性弹性力和广义非线性阻尼力的分离

橡胶球铰在外力的作用下产生非线性恢复力,在加载和卸载过程中,恢复力轨迹不重合,卸载过程与加载过程相比,恢复力存在一定的损失。从能量的观点看,加载过程存储的能量,在卸载过程中有一部分通过阻尼产生热量而耗散。加载和卸载过程中的恢复力-位移曲线,通常称为迟滞回线或滞回环,非线性的恢复力也称为滞回力。由于激励振幅、频率和预载荷的不同,滞回环的形状有所不同。本文主要研究准静态加载下的橡胶球铰非线性滞回特性,不考虑振幅、频率和预载等因素的变化对滞回特性产生的影响。

为了研究的方便,将滞回力分解为广义弹性力和广义阻尼力,如下式所示

(1)

1.2 等效线性阻尼模型

对于线性刚度、线性阻尼系统,其滞回特性曲线为如图1所示的椭圆。

图1 线刚度、线阻尼系统滞回环曲线

引入复刚度,表达式如下

K*=K′+jK″=K′+jωC=K′(1+jη)

(2)

式中:K*为复刚度;K′为存储刚度;K″为正交刚度;ω为圆频率;C为阻尼系数;η为损耗因子,且η=tanφ,φ为复刚度和存储刚度的夹角,如图2所示。

图2 复刚度示意图

椭圆的斜率为刚度,每个循环的能量消耗即为椭圆的面积,即

(3)

在加载过程中,存储的弹性能为三角形面积,即

(4)

损耗能量和加载的弹性能的比值为

(5)

故等效阻尼为

(6)

由式(6)可知,系统的等效阻尼系数与能量比、等效刚度和激励频率3个因素有关,对于任意非线性刚度、非线性阻尼系统,可通过数值积分方法求得滞回曲线包围坐标轴的面积,从而计算能量比,再通过滞回环的斜率计算等效线刚度,就可以求得系统的等效阻尼系数。

在本文的研究中,引入等效线性阻尼模型,将式(1)变形为等效线性阻尼滞回特性模型

(7)

1.3 分段线性阻尼模型

由于橡胶球铰的滞回特性具有拉压非对称特性,由试验可知,压缩过程与拉伸过程的滞回环面积并不对称。为提高模型精度,采用拉压分段线性阻尼模型

(8)

式中:Ceq1为拉伸过程等效线性阻尼系数;Ceq2为压缩过程等效线性阻尼系数。拉压过程等效线性阻尼系数可由式(6)计算。

1.4 非对称Bouc-Wen模型

经典Bouc-Wen模型为

Fh=Fk(x)+z(x)

(9)

式中:z(x)为Bouc-Wen滞回力,通过一阶微分方程求解;α、β、γ和n为Bouc-Wen模型的4个参数,α控制滞回环的斜率,β和γ控制滞回环的形状,指数n控制滞回环的光滑度。

经典的Bouc-Wen模型只能描述对称滞回曲线,利用分段拟合的思想,建立拉压分段拟合的非对称Bouc-Wen模型[9-10]如下

(10)

当x>0时,橡胶球铰处于受拉状态,i=1,Bouc-Wen模型的参数取值为α1、β1、γ1和n1;当x≤0时,橡胶球铰处于受压状态,i=2,Bouc-Wen模型的参数取值为α2、β2、γ2和n2。

1.5 高阶多项式模型

对于任意形状的曲线,可通过高阶多项式逼近,故采用多项式滞回力模型描述橡胶球铰的非线性滞回特性,即

(11)

式中:n为多项式阶次;ai、bi和ci分别为拟合的第i阶位移项、速度项和交叉项的系数。

2 滤波原理与参数识别方法

2.1 灰色Savitzky-Golay滤波方法

Savitzky-Golay滤波方法是一种局部多项式最小二次卷积拟合的数据平滑方法,通过卷积实现局部区间的多项式拟合,可以有效去除信号的高频噪声,是一种高效的信号低通滤波器[11]。Savitzky-Golay方法的原理如图3所示。将采集到的含噪信号x[n]分为若干个区间,每个区间的信号点数N=2m+1,分别对每个区间内的点进行k阶多项式拟合,拟合时通过多项式卷积快速计算多项式的系数,高效地获得滤波后各点的数值,最后将滤波后的数据重新拼接在一起,形成去噪信号s[n]。

图3 Savitiky-Golay滤波原理

应用Savitiky-Golay滤波,需要确定局部区间内的点数N和局部多项式拟合阶数k这两个重要参数。选取合适的N、k,不仅可以提高滤波去噪质量,减少信号的失真,同时还可以保证滤波效率,减少计算时间。因此,对于一组给定的信号,存在一组最优参数N、k,使得Savitzky-Golay滤波器的性能最优。

选定一个合适的去噪评价指标是进行滤波器参数优化的前提,现有的信号去噪评价指标有信噪比、信号熵、均方根等。这些评价指标在推力杆橡胶球铰恢复力、位移和速度的去噪评价中并不适合,因为不同滤波器参数下的区分度不明显。为此,本文引入灰色关联度评价指标,对去噪前后的信号进行评价。灰色关联度分析是我国学者邓聚龙教授提出的灰色系统理论的重要组成部分[12-13],灰色关联度描述的是序列之间的几何相似程度,因此采用灰色关联度评价去噪前后信号的接近程度,可以实现对滤波前后信号的宏观几何相似程度的判断,从而保证信号的较小失真和相对较好的平滑效果。

去噪前后信号的灰色关联度计算如下。

步骤1求原信号和滤波后信号的归一化序列

(12)

式中:x′[i]和s′[i]分别为归一化后的含噪信号和去噪信号;n为离散信号的总数。

步骤2求归一化后的两个信号序列之间的绝对差序列

Δ(i)=|s′[i]-x′[i]|, i=1,2,…,n

(13)

步骤3求绝对差序列的最值

(14)

步骤4计算关联系数

(15)

式中δ为分辨系数,取δ=0.5。

步骤5求灰色关联度

(16)

图4 灰色Savitzky-Golay滤波方法流程图

本文提出的灰色Savitzky-Golay滤波方法流程图如图4所示。对于给定的一组含噪信号x[n],通过调用布谷鸟算法优化程序,以去噪前后信号的灰色关联度最大化为优化目标,应用Savitzky-Golay滤波算法对信号进行滤波,通过布谷鸟算法的迭代运算获得一组最优的滤波器参数N、k对信号进行滤波,并输出滤波后的信号s[n]。

2.2 布谷鸟优化算法

在本文的研究中有两个核心,即滤波器参数的调试和非线性迟滞模型的参数识别,这两个问题的本质都是非线性优化问题。传统的优化方法在效率和精度上有较大的缺陷,而智能算法在这类优化问题上具有明显的优势,因此本文选取布谷鸟算法这种智能算法进行滤波器的最优参数确定和非线性迟滞模型的参数识别。

布谷鸟算法由Yang等在2009年提出,是一种模拟布谷鸟寻找鸟巢放置鸟蛋以繁衍下一代的生物学行为的智能算法,算法采用Levy概率分布实现寻优轨迹的迭代更新[14-16]。布谷鸟算法构建在以下3个理想化条件的基础上:①每只布谷鸟一次只产一个蛋,并随机选择鸟巢放置;②最好的鸟巢(解)能够保留到下一迭代过程;③可用的鸟巢数是固定的,且以pa为巢主鸟发现外来鸟蛋的概率。通常,取pa=0.25。在鸟蛋被巢主鸟发现后,有丢弃寄生鸟蛋或者新建鸟巢两种选择。

算法的寻优路径位置更新公式如下

⨁L(λ)

(17)

L～u=t-λ,λ∈(1,3]

(18)

其中u∈[0,1]且服从均匀分布。在更新位置坐标后,若u>pa,则重新随机生成一组新位置,并计算适应度值,与上一次迭代的适应度值比较,保留适应度大的位置,通过不断地迭代实现适应度函数的寻优,直至满足收敛条件或达到最大迭代次数,停止迭代,输出最优解。

在本文的研究中,推力杆试验数据最优滤波参数优化的适应度函数为灰色关联度的倒数,而参数识别时适应度函数为模型计算结果和试验结果误差的平方和,优化问题最终都转化为极小寻优问题。

3 模型与试验结果对比

3.1 推力杆滞回特性试验

为研究商用车推力杆的纵向迟滞特性,试验在电液伺服试验台上进行,试验原理图如图5所示,试验现场图如图6所示。试验通过夹具将V型推力杆固定在试验台架上,通过控制电液伺服系统进行拉压载荷的加载,并通过位移传感器和力传感器测量试验过程中的位移和力信号。试验时加载的载荷为准静态斜坡力信号,载荷变化可分为4个阶段,即0→150→0→-150→0 kN,完成一个拉压周期的加载。一个周期共254 s,采样频率为10 Hz,故一个周期内采集到的力信号和位移信号的样本点数为2 540。

图5 V型推力杆滞回特性试验原理图

图6 V型推力杆滞回特性试验现场图

3.2 试验数据滤波去噪处理

试验采集到的信号是含噪的力信号和位移信号,为了研究推力杆的纵向滞回特性,需要提供准确的力、位移和速度信号。因此,有必要对试验采集到的力信号和位移信号进行滤波,去除信号的毛刺、尖峰和异常点,并通过位移信号的差分计算获得速度信号。

采用本文提出的灰色Savitzky-Golay滤波方法对试验采集到的位移信号进行滤波去噪。图7所示是不同的滤波器参数N、k下去噪结果与原信号的灰色关联度三维曲面,由图可知在区间点数较大而局部拟合维度较小时,去噪前后信号的灰色关联度最大。图8所示是采用最优参数的灰色Savitzky-Golay滤波方法去噪后的位移信号,由图可知,滤波器实现了对采集到的位移信号的有效滤波,在去除了信号中毛刺的同时,最大程度地保留了位移信号的宏观曲线形状。图9所示是由原信号与去噪后信号相减获得的位移噪声信号,由图可知,位移噪声除了在载荷的拐点有尖峰外,其余部分为随机噪声。为进一步研究噪声的分布情况,采用统计学方法进行分析。图10是位移噪声信号的平滑误差频数图,由图可知,噪声信号呈现参数为N(0,σ2)的高斯正态分布,图中曲线是位移噪声的正态分布密度的拟合曲线。

图7 不同参数对位移信号滤波效果的影响

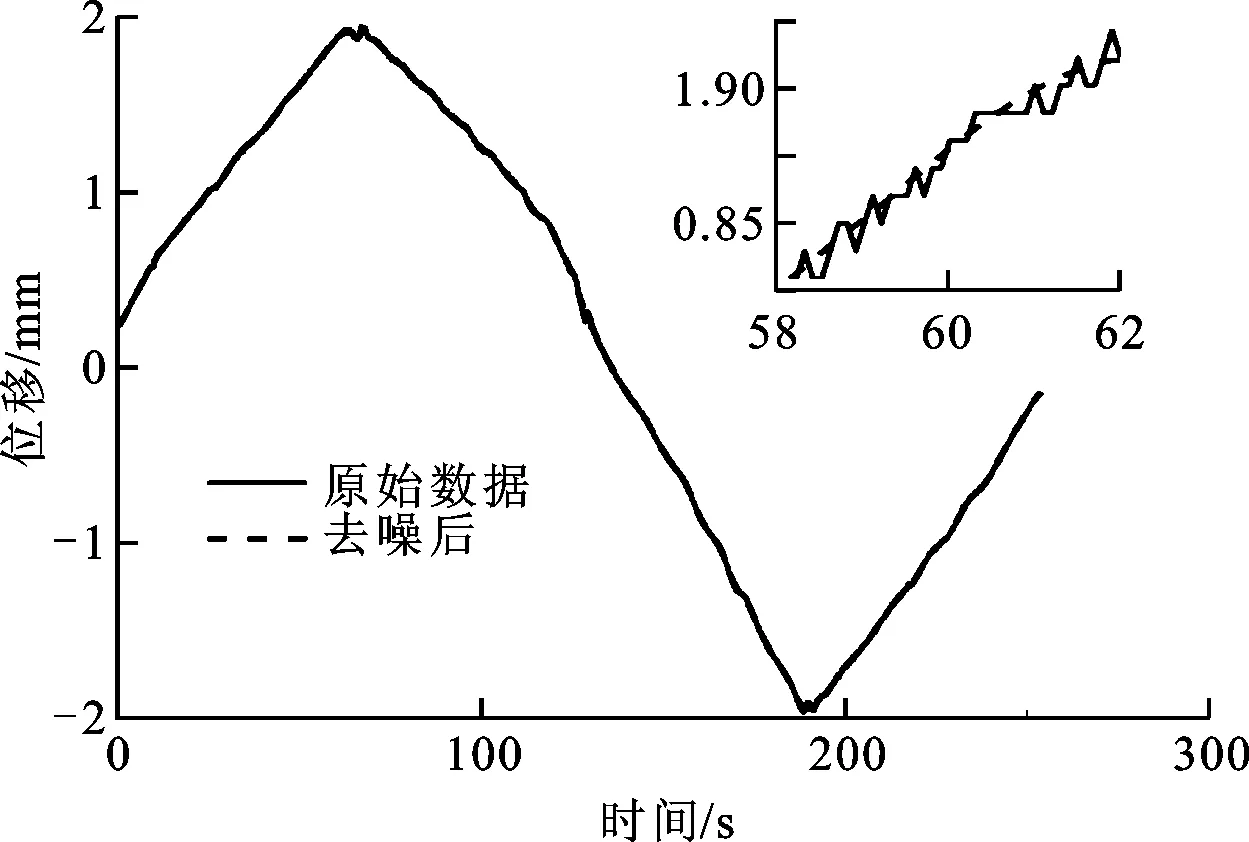
图8 滤波前后的位移信号对比图

图9 位移信号噪声时域图

图10 位移信号噪声统计特性

图11所示是不同滤波器参数对去噪前后速度信号的灰色关联度影响曲面图,与位移信号滤波器参数有类似的规律。图12所示是滤波后速度信号和直接对含噪位移信号差分获得的速度信号对比图,其中,一次滤波为对滤波后的位移信号进行差分计算的速度信号,二次滤波是在一次滤波获得的速度信号的基础上再次进行滤波后获得的速度信号。由图可知,一次滤波滤除了大部分的毛刺和尖峰,而二次滤波在一次滤波基础上,进一步去除了位移信号中的随机干扰噪声。图13和图14所示分别是速度噪声时域图和频数图,由图可知速度噪声也服从高斯正态分布。

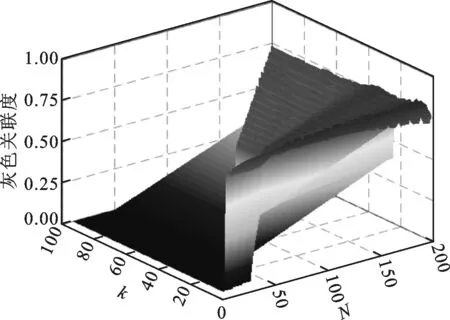
图11 不同参数对速度信号滤波效果的影响

图12 滤波前后的速度信号对比图

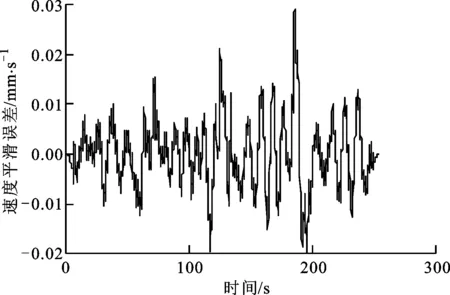
图13 速度信号噪声时域图

图14 速度信号噪声统计特性

图15 不同参数对力信号滤波效果的影响

图16 滤波前后的滞回力对比图

图17 滞回力信号噪声时域图

图15所示是力信号滤波器参数与去噪前后信号灰色关联度曲面,图16是力信号滤波前后对比图,图17和图18是力噪声时域图和频数图。力信号最优滤波器参数的规律和噪声的统计分布特性与位移、速度噪声类似,不再赘述。

图18 滞回力信号噪声统计特性

表1所示是采用布谷鸟算法获得的最优化滤波器参数和噪声信号分布特性的统计量。由表可知,对于不同的信号,最优滤波器参数不同,这是由噪声信号和滤波方法共同决定的,采用本文所提出的布谷鸟算法优化后的灰色Savitzky-Golay滤波器能够根据不同的含噪信号特征,采取最优的滤波参数,在去除噪声的同时,保留信号的宏观几何特征,减少信号的失真。

表1 布谷鸟优化的滤波器参数

图19所示是滤波前后的推力杆力-位移滞回特性曲线,由图可知,滤波后的滞回环不存在明显的毛刺和尖峰,而滤波前后滞回环的宏观几何特征很好地保留了下来。图20所示是采用式(1)的广义非线性弹性力和广义非线性阻尼力分解出的弹性力和实测滞回力的对比图,在分解出了广义弹性力后,后文分别采用不同的模型对剩余的广义非线性阻尼力进行拟合。

图19 滤波前后的总体滞回特性曲线

图20 分解出的非线性弹性力与实测滞回力的对比

图21 等效线性模型对阻尼力的拟合效果

3.3 等效线性模型与实测结果对比

图21是采用等效线性模型式(7)对阻尼力的拟合效果,由图可知,等效线性模型使用一个等效的椭圆对不规则的迟滞阻尼环进行拟合,椭圆包围的面积与阻尼滞回环包围的面积相等。图22和图23分别是阻尼力和总体力-位移滞回环的拟合效果,由图可知,等效线性模型可以对阻尼力和滞回环的趋势进行拟合,但精度较差,且在等效计算过程中,将非对称的迟滞特性平均等效而抹除了其非对称特性。

图22 等效线性模型仿真的阻尼力时域曲线

图23 等效线性模型仿真的总体迟滞环

图24 分段线性模型对阻尼力的拟合效果

图25 分段线性模型仿真的阻尼力时域曲线

3.4 分段线性模型与实测结果对比

图24所示是根据式(8)所述的分段线性模型进行的阻尼力的拟合效果,由图可知,分段线性模型使用两个等效的半椭圆对不规则的迟滞阻尼环进行拟合。两个半椭圆包围的面积分别与拉压过程的阻尼滞回环包围的面积相等。图25和图26所示分别是阻尼力和总体力-位移滞回环的拟合效果,由图可知,分段线性模型可以对阻尼力和滞回环的趋势进行较好地拟合,其精度较等效线性模型有所提高,且可以用于描述推力杆纵向拉压的非对称迟滞特性。

图26 分段线性模型仿真的总体迟滞环

图27 非对称Bouc-Wen模型对阻尼力的拟合效果

3.5 非对称Bouc-Wen模型与实测结果对比

采用布谷鸟算法,对非对称Bouc-Wen模型的参数进行识别。图27所示是根据式(10)所述的非对称Bouc-Wen模型进行的阻尼力的拟合效果,由图可知,非对称Bouc-Wen模型使用两个等效的半曲线对不规则的迟滞阻尼环进行拟合,两条曲线包围的面积分别与拉压过程的阻尼滞回环包围的面积相等。图28和图29所示分别是阻尼力和总体力-位移滞回环的拟合效果,由图可知,非对称Bouc-Wen模型可以对阻尼力和滞回环的趋势和数值进行较好地拟合,其精度高于分段线性模型,且可以用于描述推力杆纵向拉压的非对称迟滞特性。

图28 非对称Bouc-Wen模型仿真的阻尼力时域曲线

图29 非对称Bouc-Wen模型仿真的总体迟滞环

图30 多项式模型对阻尼力的拟合效果

3.6 高阶多项式模型与实测结果对比

应用式(11)的高阶多项式模型对滤波后的数据进行模型参数识别,发现采用12阶多项式可以对阻尼力进行很好的拟合。图30所示是高阶多项式模型拟合的阻尼力效果图,由图可知,高阶多项式模型使用高阶的多项式生成的不规则曲线对不规则的迟滞阻尼环进行高度逼近,两条曲线包围的面积分别与拉压过程的阻尼滞回环包围的面积相等。图31和图32所示分别是阻尼力和总体力-位移滞回环的拟合效果,由图可知,高阶多项式模型可以对阻尼力和滞回环的趋势和数值进行很好地拟合,其精度高于其他3个模型,且可以用于描述推力杆纵向拉压的非对称迟滞特性,但由于模型是高阶多项式模型,参数较多,参数识别难度大,增加了模型的复杂度。

图31 多项式模型仿真的阻尼力时域曲线

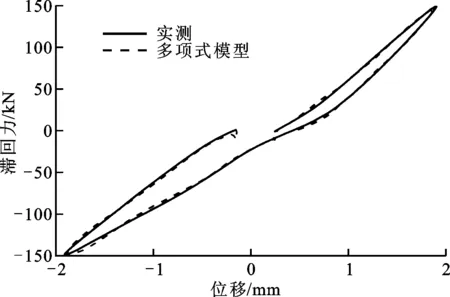
图32 多项式模型仿真的总体迟滞环

3.7 4种模型对比

表2所示是4种不同模型的精度和复杂度对比情况。由表可知,随着模型参数的增加,模型的精度有所提高。等效线性模型所需的参数数量最少,复杂度最小,而精度也较低。等效线性模型适合于定性地分析迟滞特性,不适合精度要求较高的仿真计算。在满足一般工程计算精度要求的情况下,可以选取分段线性模型或者非对称Bouc-Wen模型进行非对称迟滞特性的仿真。若要求进一步提高计算精度,可采用高阶多项式模型进行拟合。