考虑转捩的SST模型在冲击射流传热中的应用

黄华坤,孙铁志,尤天庆,张桂勇,3,4,回达,宗智,3,4

(1.大连理工大学船舶工程学院,116024,辽宁大连;2.北京宇航系统工程研究所,100076,北京; 3.大连理工大学工业装备与结构分析国家重点实验室,116024,辽宁大连; 4.高新船舶与深海开发装备协同创新中心,200240,上海)

冲击射流由于具有强烈的换热效果,受到了各行业的广泛关注[1]。对于垂直或短距起降(V/STOL)的军用飞机,射流与地面之间的相互作用对飞机的设计具有重要的影响[2]。在航母上起降的V/STOL飞机不仅牵涉到飞机本身,更有可能影响到甲板结构的安全。除此之外,冲击射流原理广泛应用于造纸、纺织等涉及到的干燥、冷却和加热等工业过程。

早期的研究表明,使用k-ε模型在传热问题的预测上与实验值偏差很大,而且在冲击距离较短时无法准确地预测出努塞尔数Nu的第二峰值[2-6]。此外,前人的研究表明标准两方程模型容易过高预测滞止点附近的湍动能[7]。Kato和Launder从滞止点附近的流体趋于无旋、涡量趋于零的角度出发,提出了基于涡量和应变的湍动能产生项,以降低滞止点附近湍动能的生成[8]。因而,Kato-Launder模型被推荐应用于冲击射流问题[9]。

然而,努塞尔数第二峰值依然很难被湍流模型准确地预测到。研究表明,努塞尔数第二峰值受层流到湍流转捩的影响[10]。Uddin等通过LES模型进一步揭示了涡的形成和发展对努塞尔数第二峰值的影响[11]。Sharif等在研究中指出具备计算层流到湍流转捩能力的模型能更好地预测努塞尔数第二峰值[12],当前广泛使用的转捩模型为低雷诺数湍流模型。低雷诺数转捩模型是一种基于黏性底层特性、通过阻尼因子修改底层湍流黏度的方法来模拟转捩的模型,因此模拟转捩的能力有限[13]。Dutta等通过数值计算表明,使用低雷诺数SSTk-ω模型能获得和非转捩模型相比更准确的努塞尔数分布[14]。然而,在冲击距离增大时,低雷诺数SSTk-ω模型的预测能力差于标准k-ε和k-ω模型,因为低雷诺数SSTk-ω模型预测了伪二次峰值。

因此,准确地模拟冲击射流的传热现象仍然是国内外学者重点关注的问题。本文在文献[15]推荐的SSTk-ω模型的基础上,加入了Kato-Launder模型以避免湍流模型过高地预测滞止点附近的湍动能。同时,为了更好地预测层流到湍流的转捩过程,将一方程湍流间歇转捩模型加入到求解方程中,并通过与实验数据对比来评价改进的SSTk-ω湍流模型在射流冲击问题中的适用性。一方程间歇转捩模型是基于层流到湍流的转捩机理,利用间歇因子控制湍流的生成,同时基于经验公式对转捩过程进行求解而建立的模型[16]。基于建立的数值方法探究了不同冲击高度下压力梯度对努塞尔数第二峰值的影响,获得的结果可丰富射流换热问题的机理内涵。

1 数值计算方法

1.1 基本控制方程

控制方程包括连续性方程、动量方程和能量方程,表达式如下

(1)

(3)

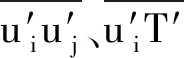
1.2 SST k-ω湍流模型

SSTk-ω模型是由Menter提出的一种基于标准k-ε模型和k-ω模型的混合模型[17],因此SSTk-ω模型在壁面射流区能准确地预测流动特征,同时可避免对远场边界条件的敏感性。该模型还添加了逆压梯度修正项,这使得SSTk-ω模型广泛应用于如冲击射流等逆压梯度和分离流问题中。除了前面提到的控制方程外,为封闭模型,在模型中增加了湍动能k和比耗散率ω,表达式如下

(4)

(5)

Gω-Yω+Dω+Sω

(6)

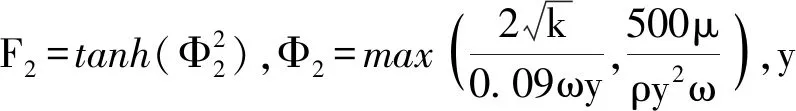
1.2.1Kato-Launder模型SSTk-ω等两方程普遍存在的一个问题是产生了过高的湍动能[7],导致SSTk-ω模型在滞止点处预测的传热率过高。Kato和Launder对产生的湍动能项进行了如下修正[8]

Gk=μtS2

(7)

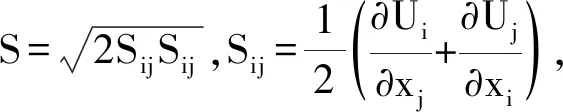
Gk=μtSΩ

(8)

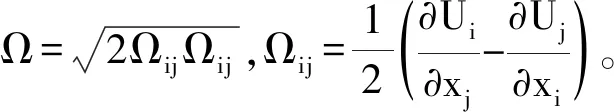
1.2.2 湍流间歇转捩模型 间歇转捩模型从TransitionSST模型中发展而来,该模型考虑了自然转捩、分离流转捩[18]和横流不稳定[7]等多种转捩机制,被广泛用于三维机翼转捩预测问题。间歇转捩模型的输运方程如下

(9)

在转捩模型的源项中,通过式(10)触发该模型

Reθc(Tu,λθ)=CTU1+CTU2exp[-CTU3TuFPG(λθ)]

(10)

式中:Reθc表示临界动量厚度雷诺数;Tu和λθ分别表示逼近自由湍流强度和压力梯度的局部变量;FPG的定义参见文献[7]。

1.3 改进的SST k-ω湍流模型

如前所述,SSTk-ω模型一方面结合了标准k-ω模型和k-ε模型的优点,另一方面增加了对逆压梯度的修正项,如式(4)所示。逆压梯度修正被认为是SSTk-ω模型能准确预测冲击射流传热和流动的原因之一[19]。然而,SSTk-ω模型中式(5)的应力项S在滞止点附近往往过大,使得湍动能产生项Gk偏大,导致SSTk-ω模型难以预测有涡脱落的流动[8],同时在滞止点处产生过高的传热率。对于Kato-Launde模型,从式(7)和式(8)中可以看出其降低了湍动能的产生,特别是在滞止区流动趋于无旋时,Ω将趋于0。

尽管如此,Wienand等同时对SSTk-ω模型以及Kato-Launder模型进行了研究,发现努塞尔数第二峰值依然难以被准确地捕捉[9]。由于第二峰值与转捩相关,因此间歇转捩模型的引入有可能提高模型对转捩的预测能力。考虑到冲击射流涉及到强逆压梯度、流动分离和涡的形成与发展,因此将上述3种模型进行结合可能会提高其对冲击射流传热的预测能力。基于以上讨论,将Kato-Launder模型和间歇转捩模型与式(5)进行耦合,如下所示

(11)

(12)

(13)

1.4 计算模型及求解设置

计算模型如图1所示,其中喷嘴的宽度为B,长度L=50B。由于计算模型关于y轴对称,为提高计算效率,建立1/2模型进行计算。

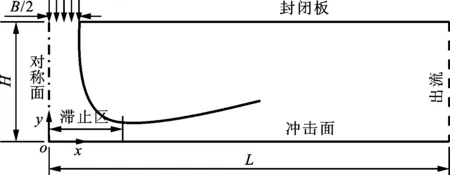
图1 计算模型和边界条件

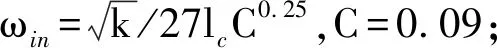
本文计算选择基于压力基的稳态求解器,即SIMPLE算法。梯度离散格式采用LeastSquaresCellBased,压力离散格式采用PRESTO,动量和湍动能等采用二阶迎风格式。

1.5 网格划分及无关性验证

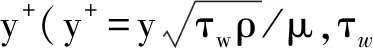
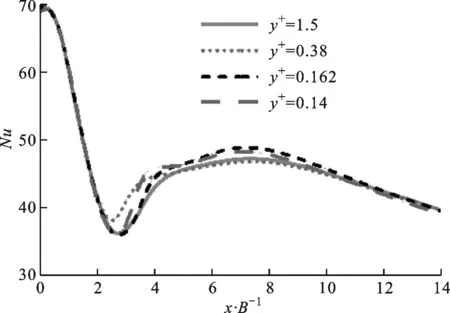
图2 网格无关性验证

从图2中可以看出,4种网格计算得到的努塞尔数在滞止点处基本重合,其中y+=0.162和y+=0.14的网格在x/B=3处的相对误差为3%,在x/B=7.4处的相对误差为1.1%,两种网格的努塞尔数分布曲线基本重合,可认为此时的解已满足网格无关性要求。因此,在没有特别声明的情况下,后续研究选取y+=0.162作为H/B=4时的计算网格。

2 结果分析与讨论

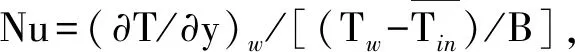
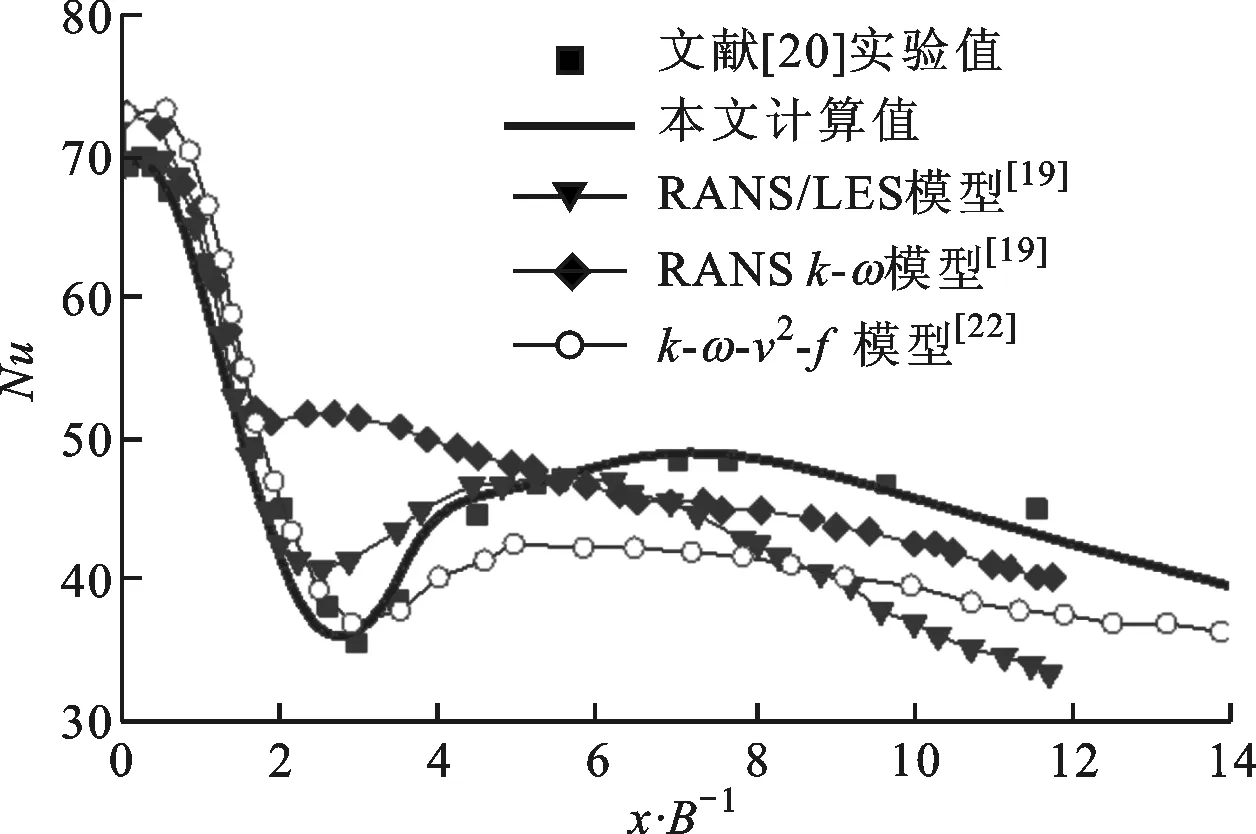
图3 Re=20 000、H/B=4时数值计算结果与 实验数据的对比

2.1 温度场分析

图3给出了H/B=4时采用不同模型计算得到的努塞尔数与实验数据的分布情况。从图中可以看出,在x/B=3的位置努塞尔数达到极小值,随后传热率逐渐增大,在x/B=7处达到第二峰值。介于二次峰值和极小值之间的区域称为转捩区(3≤x/B≤7.4)。在滞止点处,传热率与湍流强度紧密相关,较高的湍流强度引起湍动能的过快增长,导致传热率增加。此外,来自上游的湍动能传递到下游,从而引起转捩的发生。从图3中可以看到,在滞止区,图中所列的模型基本都准确地预测了努塞尔数。这是因为在基于k-ω的模型中,通过限制涡黏系数(式(4))来限制雷诺应力过快增长的方法被广泛地使用,保证了该区域处于较低湍流度的状态[17],从而达到了限制湍动能的目的。同时,改进的SSTk-ω模型由于Kato-Launder模型的作用,预测的努塞尔数比RANSk-ω模型和k-ω-v2-f模型要低,但更符合实验结果。在转捩区,RANS/LES模型、k-ω-v2-f模型和本文改进的SSTk-ω模型都准确地捕获了转捩点(x/B=3)。然而,在第二峰值的预测上,图3中各模型表现出了明显的差异,其中RANSk-ω模型、k-ω-v2-f模型和RANS/LES模型均无法准确地捕捉到努塞尔数的第二峰值的大小和位置,而对于改进的SSTk-ω模型,由于转捩模型的加入,以及在滞止点处准确地预测了第一峰值,从而准确地捕捉到了转捩点。这说明改进的SSTk-ω模型准确地预测了一个应力场,在应力作用下,湍流强度逐渐增大从而导致转捩的发生。同时,在2≤H/B≤4的范围内,RANSk-ω模型获得的传热率高于改进的SSTk-ω模型,可能的解释是改进的SSTk-ω模型在式(4)中增加了逆压梯度修正。这是因为在逆压梯度层中,湍动能的产生大于耗散[23],如果不加以修正,则其预测的湍动能往往过高。因此,如前面分析,这也是SSTk-ω模型被推荐用于冲击射流传热预测的原因之一。在第二峰值附近,受涡破碎的影响,Kato-Launder模型中的涡量随着涡的破碎而增大,湍动能的生成项变大,从而引起传热率增大。改进的SSTk-ω模型在滞止点处准确地预测了努塞尔数,并且成功预测了努塞尔数第二峰值的位置及其分布;与实验得到的努塞尔数最小值位置相比,计算得到的最小值位置在x/B=2.77处,相对误差为7.6%,第二峰值的位置为x/B=7.30,相对误差为1.35%。由于RANSk-ω模型对转捩预测的能力较弱,因此基于RANSk-ω模型的RANS/LES模型和k-ω-v2-f模型均是在靠近壁面附近采用RANSk-ω模型,在边界层外采用LES模型或者v2-f模型,因此这种在不改变黏性层的情况下对模型进行的改进,很难准确地预测努塞尔数第二峰值现象。

2.2 速度场分析

(a)x/B=1

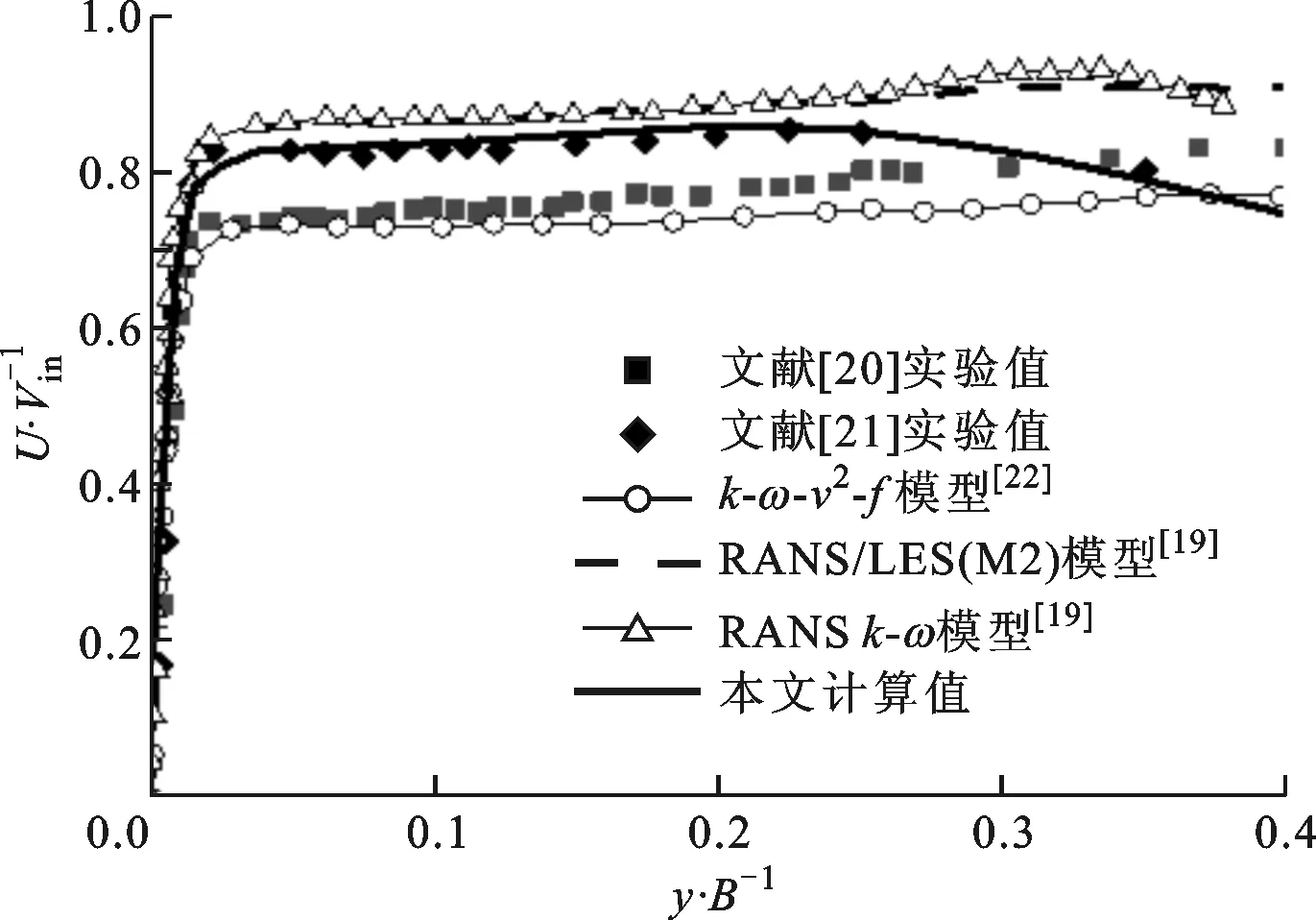
(b)x/B=2

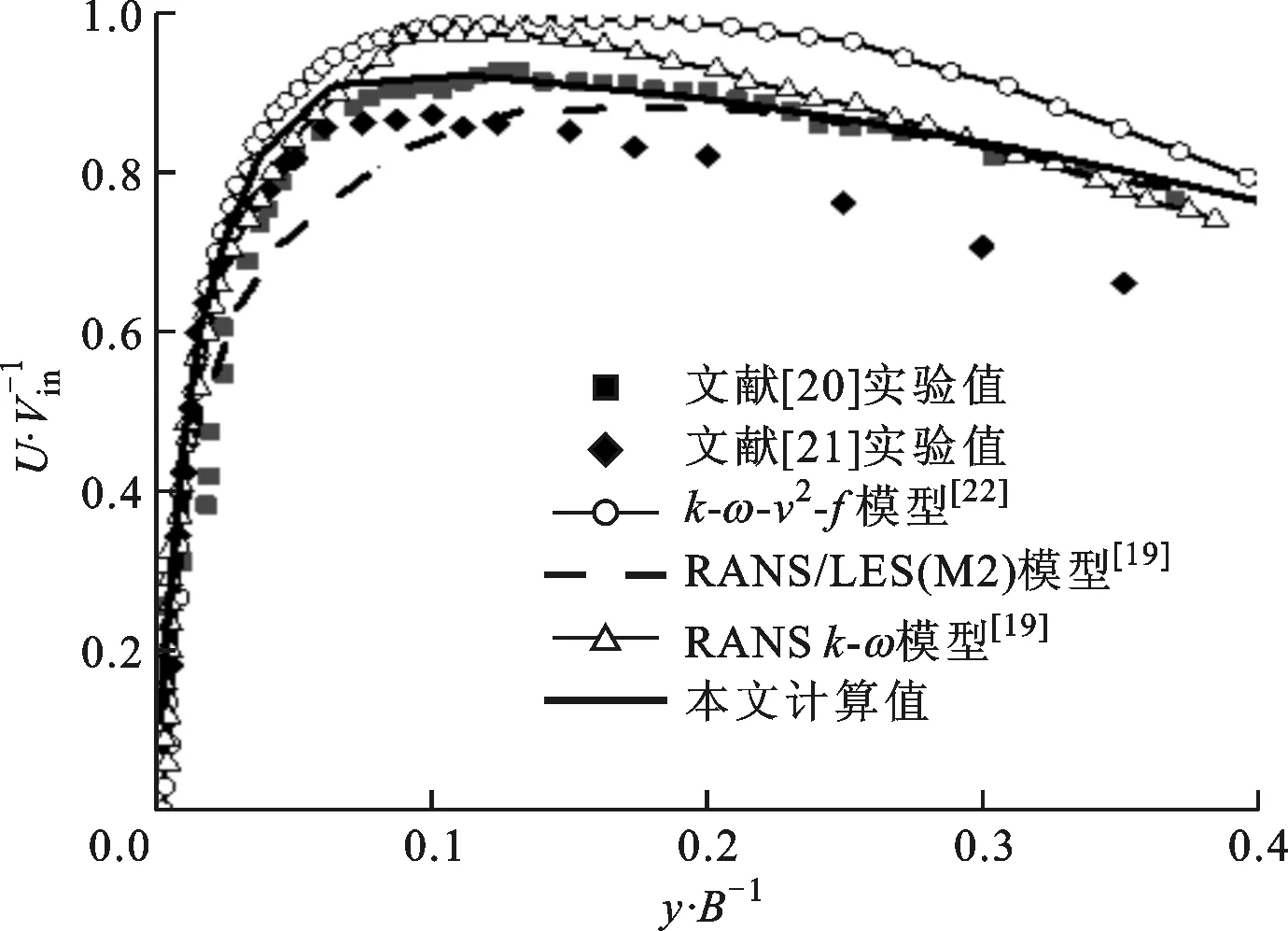
(c)x/B=5

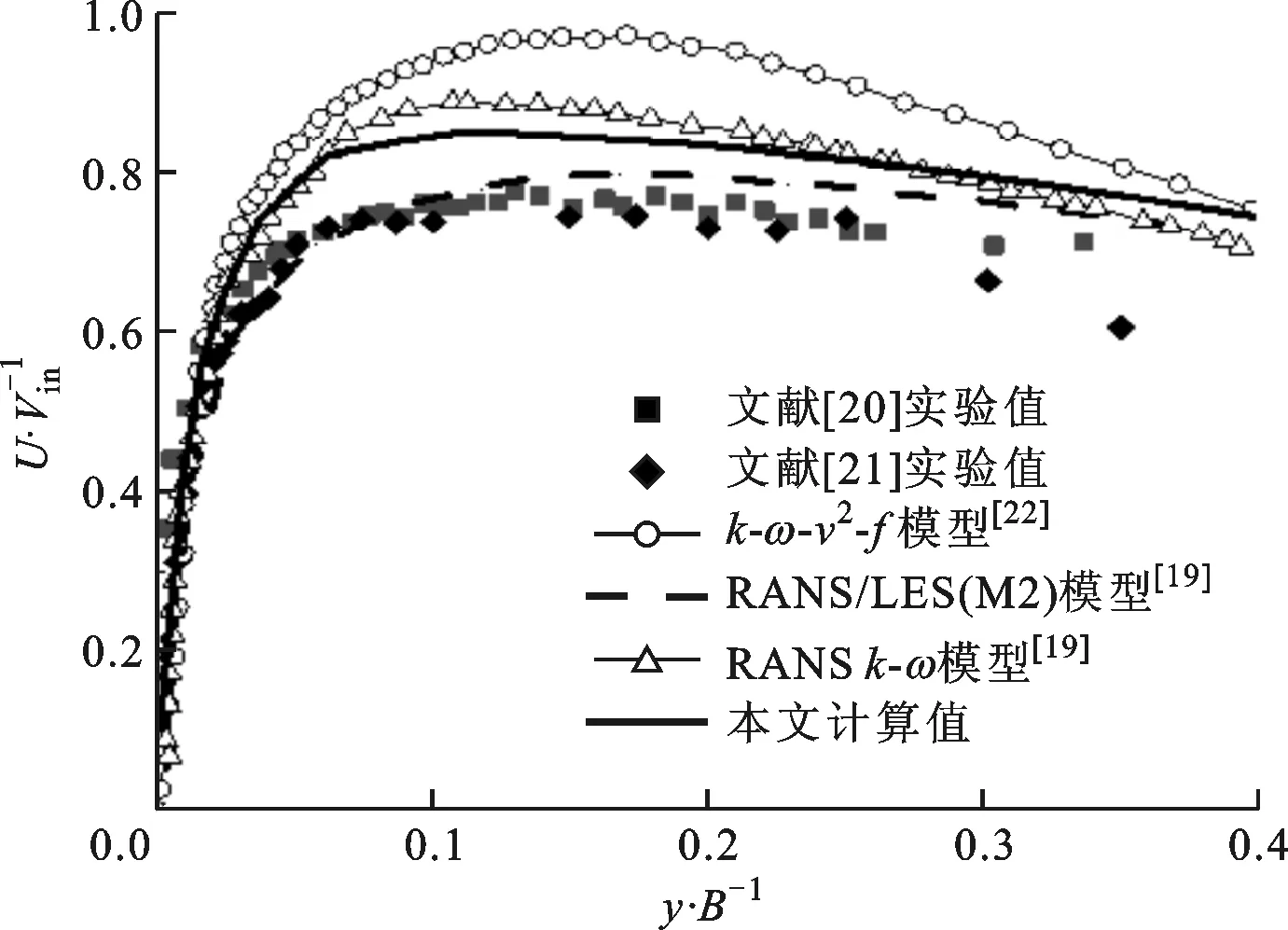
(d)x/B=7图4 Re=20 000、H/B=4情况下x方向的归一化平均速度沿y方向的分布

为了尽可能地考虑实验的不确定性因素,将数值计算结果与Ashforth等[20]和Zhe等[21]的实验数据均作了对比。图4给出了x方向的归一化平均速度U/Vin沿y方向的分布情况。在滞止区附近,由于流线的聚集,产生了一个较大的应力场[21]和较低的湍流强度,离滞止点越远,应力越小。因此,流动方向的法向速度梯度从一个极大值向出口方向逐渐降低,如图4所示。由于应力的影响,湍流强度随着x/B的增加逐渐变大,从而促使了转捩的发生。在x/B=5和x/B=7两个位置,可以明显看到减速区的存在。减速区的形成受涡发展的影响[24]。在x/B=1,2的位置,从前面的分析中已知,所有的模型在滞止区附近产生了一个较低的湍流强度,因此均获得了较符合实验的结果,这也同时反映在了滞止点附近对努塞尔数的预测上。随着湍流强度的增大,在转捩区x/B=5的位置,改进的SSTk-ω模型表现得最好。在x/B=7的位置,即涡结构附近[24],改进的SSTk-ω模型过高地预测了速度分布,但是仍然比传统的RANSk-ω模型和k-ω-v2-f模型更接近于实验结果,此时只有采用RANS/LES混合模型才能得到与实验较一致的结果。这是因为RANS/LES模型结合了LES模型在处理涡方面的优点,因此在该位置预测的速度也最为准确。Hadžiabdi等提供了另外一种可能的解释,他们通过LES模型对二次峰值展开研究发现,涡和壁面间的相互作用引起的流动分离造成了二次峰值的形成[25]。流动分离过程中伴随着逆压梯度的形成,压力增大,导致速度减小,可能的原因是SSTk-ω模型对逆压梯度并不是特别敏感[23],因此造成了改进的SSTk-ω模型过高地预测了速度的分布。然而,总体上看,考虑到模型的计算效率和计算精度,本文所用的湍流模型仍然有一定的优势。

2.3 不同冲击距离的影响

如前所述,努塞尔数第二峰值归因于层流到湍流之间的转捩。然而,Hadžiabdi等认为流动的分离才是努塞尔数第二峰值产生的原因[25]。结合以上两种观点,说明SSTk-ω模型和转捩模型相结合,能较好地预测努塞尔数第二峰值的特征及其分布,但是对于速度场的预测,在第二峰值附近,预测的速度依然偏大。为了进一步研究流动分离对努塞尔数第二峰值的影响,在前面的基础上,选取H/B=2,4,9.2进行计算。对应的雷诺数为20 000。图5显示了不同冲击距离下努塞尔数的分布情况。从图中可以看出,在H/B=9.2时,努塞尔数第二峰值消失,在H/B≤4时,努塞尔数第二峰值较为明显。

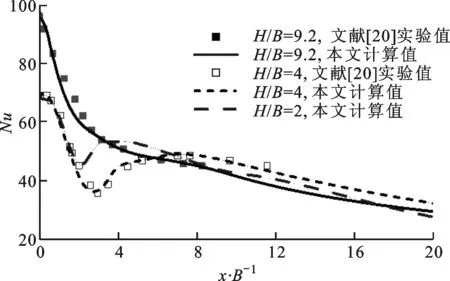
图5 不同冲击距离下的努塞尔数分布

(a)H/B=2

(b)H/B=4

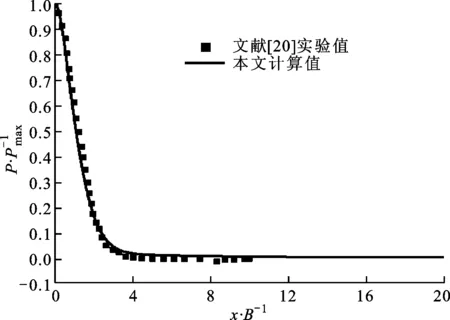
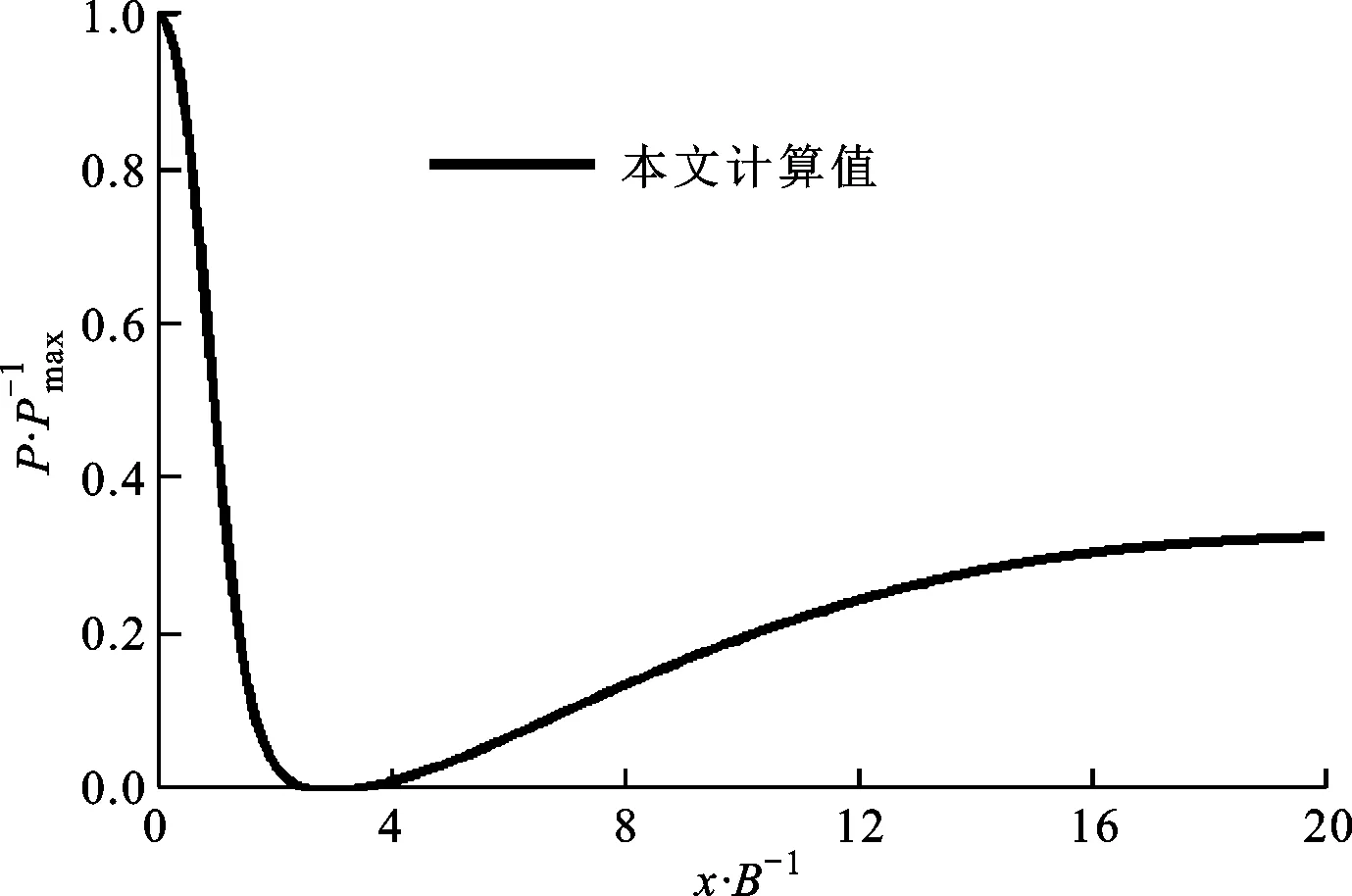
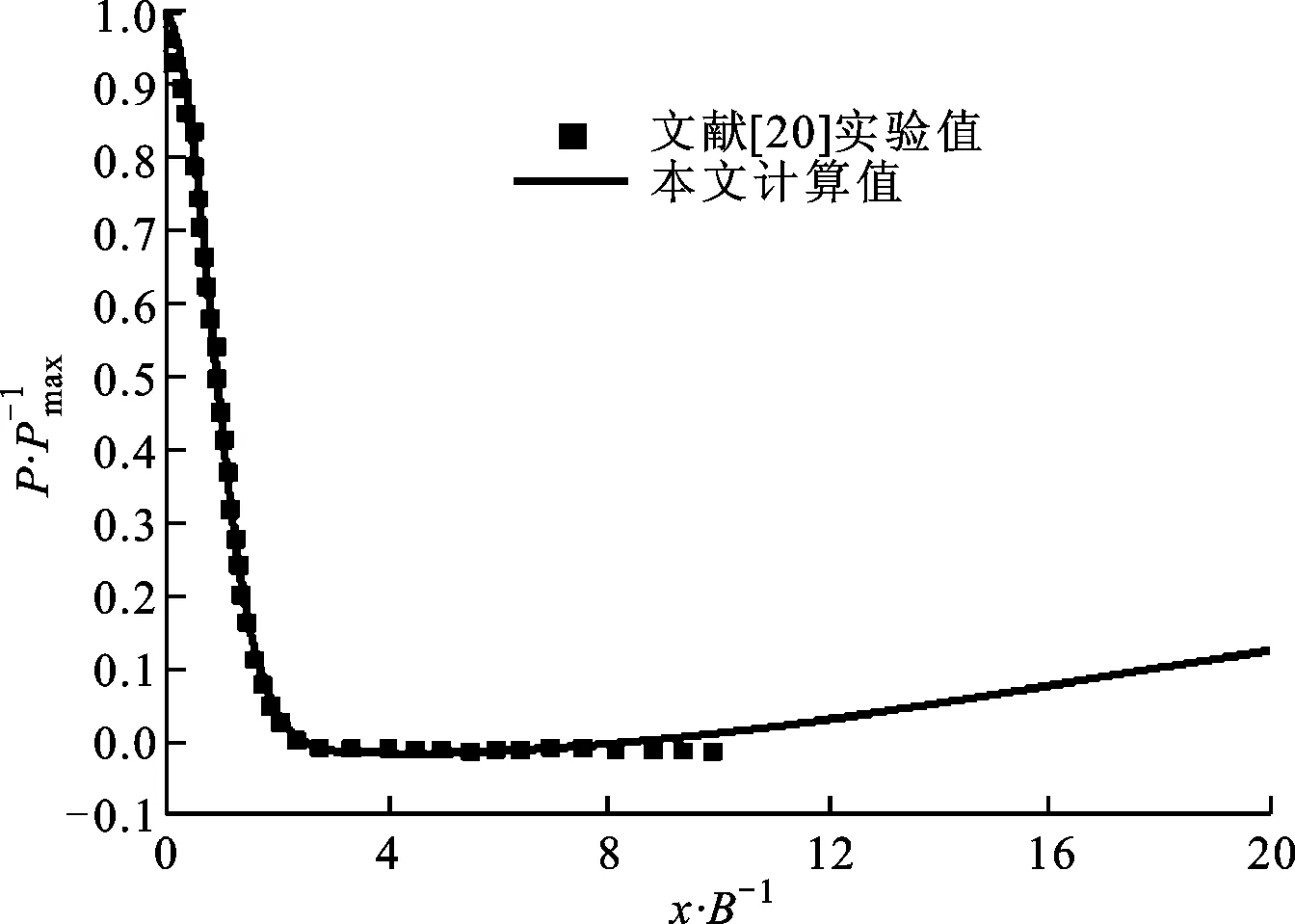
(c)H/B=9.2图6 不同冲击距离下沿冲击面的压力分布

图6显示了不同冲击距离下压力沿冲击面的分布情况,其中P表示压力,Pmax表示滞止点处的压力。从图中可以看出:当H/B≤4时,在下游区域,压力逐渐增大,预示着逆压梯度区的存在,从而导致速度降低;当H/B=9.2时,下游压力几乎不变,相对应地,努塞尔数第二峰值也消失了。在滞止点附近,压力急剧地减小,由此形成了速度加速区,如图4所示。因此,可以认为逆压梯度和努塞尔数的第二峰值也存在着一定的联系,当下游区的逆压梯度消失,不存在流动分离时,努塞尔数第二峰值也会随着消失。

3 结 论

本文基于RANS方法,提出了一种改进的SSTk-ω模型计算了H/B=4时带有封闭板的平板冲击射流问题。通过将计算得到的温度分布和速度分布与实验数据对比,在二维平板冲击射流传热问题方面验证了改进模型的有效性,在此基础上研究了不同冲击距离下压力梯度对努塞尔数分布的影响。通过本文的研究工作,得到以下主要结论。

(1)改进的SSTk-ω模型与其他模型相比能够更准确地预测努塞尔数的分布以及第二峰值的位置。

(2)在速度预测方面,与RANSk-ω和k-ω-v2-f模型过高地预测速度分布相比,带有附加模型的SSTk-ω模型给出了与RANS/LES模型基本相当,更符合实验的结果。

(3)当H/B≤4时,努塞尔数分布表现出明显的第二峰值的特征,此时在二次峰值附近存在着逆压梯度区;随着冲击距离的增大,逆压梯度区消失,努塞尔数第二峰值也随着消失。