δ-Pu空位缺陷的密度泛函理论计算

李大伟, 高云亮, 董三强， 朱芫江， 李进平

(1. 火箭军工程大学，西安 710025； 2. 中国科学院力学研究所 高温气体动力学国家重点实验室，北京 100190)

1 引 言

点缺陷是晶体中最基本的缺陷形式，也是形成其它高维度缺陷的基础. 一般而言，晶体中点缺陷的浓度很低，但却对其性质有着很大的影响[1]. 从室温到913 K(Pu的熔点)的较小范围内，Pu存在α、β、γ、δ、δ′、ε等6种同素异晶体，其中δ-Pu的力学性能和机械加工性能最好，应用也最为广泛. 在δ-Pu中存在自间隙原子和空位两种本征缺陷，其中空位易与材料辐照老化产生的He结合形成团簇，进而发展成为氦泡，对材料的结构和性能造成显著影响[2,3]. 当前对于Pu中缺陷的研究主要集中于氦点缺陷和氦泡的形成机理以及对基体物性的影响[4-6]，对空位的影响及其机理研究还比较少见.

自1941年发现以来，钚及其化合物的性质研究就受到广泛重视. 然而，由于Pu的放射性、毒性以及复杂的物理性质和化学性质，精密的实验研究面临很大困难. 尽管目前在Pu的宏观性质研究方面已经取得了许多研究成果，但对其机理仍然缺乏足够深入的认识[7]，因而发展具有预测能力的理论研究方法越来受到研究人员的重视. 在点缺陷研究方面，Robinson等[8]采用修正嵌入原子法(Modified Embedded Atom Method，MEAM)计算了δ相Pu-Ga合金中点缺陷的形成能和扩散势垒，发现缺陷的形成能与缺陷的种类和其所处环境密切相关. Ao等[9]利用分子动力学方法(Molecular Dynamics, MD)研究了晶界点缺陷的性质，发现晶界点缺陷的形成能一般低于晶格内部缺陷的形成能，且晶界不同位置点缺陷的形成能也不相同. 密度泛函理论(DFT)是目前凝聚态物理的主流计算方法，研究人员利用该方法对Pu及其化合物的许多性质进行了成功的计算[10-15]. 为研究空位缺陷对δ-Pu结构稳定型和电子结构等性质的影响，本文采用基于密度泛函理论的第一性原理方法，计算了含有空位缺陷的δ-Pu晶体的结构参数、结合能、空位形成能以及电子结构，探讨了空位缺陷对δ-Pu物性影响的机制.

2 理论模型与计算方法

δ-Pu为面心立方结构，空间群为Fm3m，晶格常数为0.4637 nm. 本文利用基于δ-Pu单胞扩展的方法，构建了1×1×2、2×2×1和2×2×2的超胞，并删除中心位置的Pu原子，形成了空位浓度分别为12.5%、6.25%和3.125%的超胞模型，各含缺陷模型以及不含缺陷的δ-Pu超胞模型如图1(a)-1(d)所示.

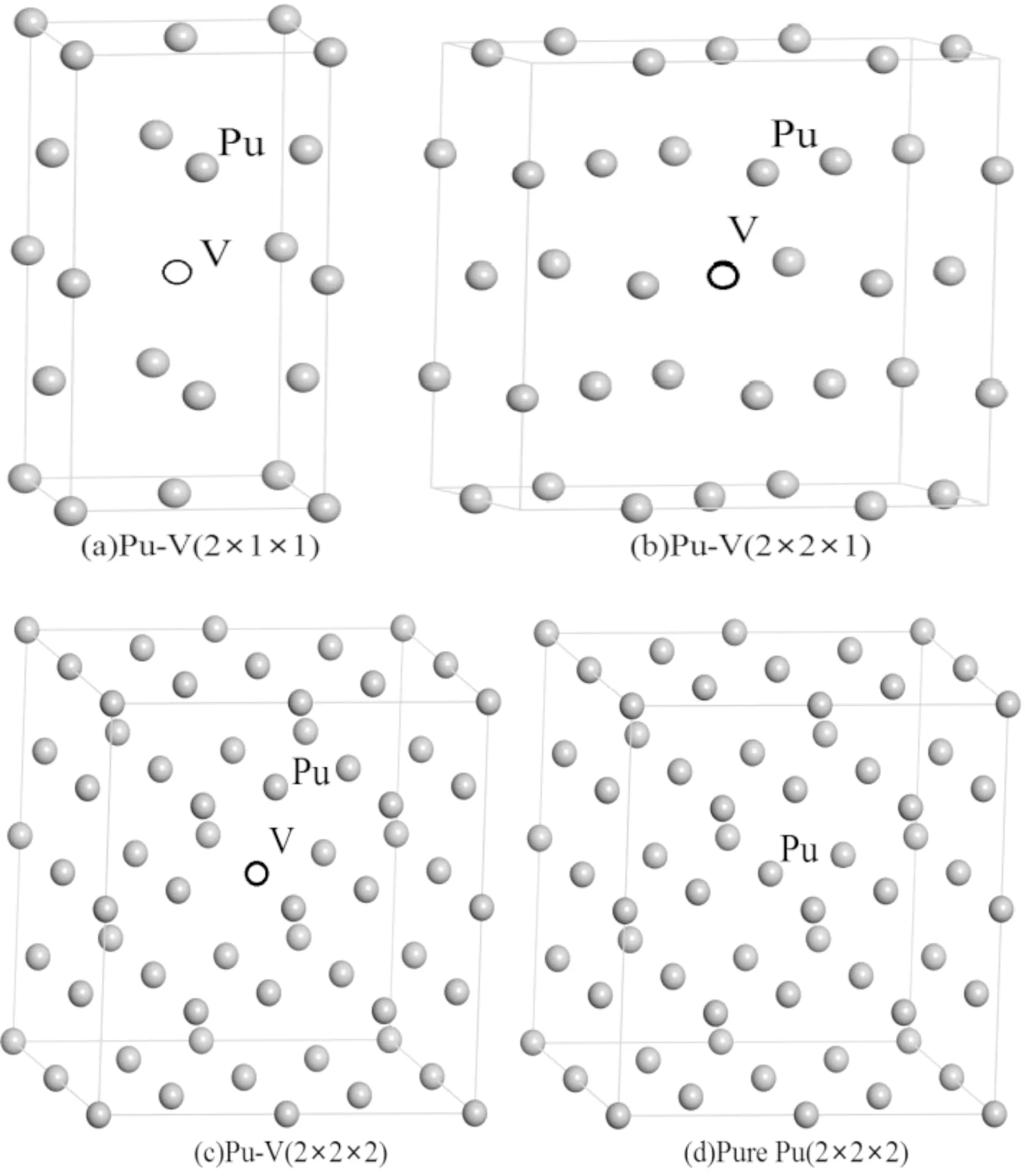
图1 含空位和不含空位的δ-Pu超胞模型Fig. 1 Supercell models of δ-Pu with and without vacancy

本文采用基于密度泛函理论的平面波赝势方法，选取Pu原子的价电子组态为Pu5f66s26p67s2，并采用超软赝势(Ultrasoft pseudopotentials, USP)[16]描述价电子和离子实之间的相互作用. 对模型的几何优化采用BFGS算法[17]，并在自旋极化(Spin Polarized，SP)条件下，选用局域密度近似(Local density approximation, LDA)为交换关联函数. 平面波截断能取为550 eV. 布里渊区的特殊k网格点取样采用Monkhorst-Pack方案[18]，对于1×1×2、2×2×1和2×2×2的晶胞，k网格分别取为8×8×4、4×4×8和4×4×4，为保证精度，对截断能和k网格都进行了收敛性测试. 自洽收敛能量精度取为1×10-6eV/atom，计算在倒易空间中进行. 锕系金属为强关联电子体系，5f电子的库伦作用很强，传统的局域密度近似和广义梯度近似(Generalized Gradient Approximation, GGA)均无法准确描述其电子特性，因而计算电子结构时，引入Hubbard参数U来描述这种强关联作用，即LDA+U或GGA+U方法[19]. 本文中电子结构的计算采用GGA+U方案，它包括两部分，即对于非局域化的s、p和d电子仍按GGA方法处理，而对于局域性强的5f电子则采用Hubbard模型处理. 本文的计算中，U的值采用文献[20]和[21]中使用的4.00 eV.

3 结果与讨论

3.1 晶体结构和稳定性分析

首先对含缺陷和等大的不含缺陷的晶胞进行了几何优化，使结构充分弛豫，优化后的折合晶格常数和体积如表1所示. 由表可见，对于各不含缺陷的模型，计算得到的折合晶格常数均约为0.4740 nm，与实验值0.4637 nm非常接近，偏差为2.2%，表明本文的计算条件设置是合理的. 进一步分析可知，空位使模型的晶格常数和体积减小，且随着模型的增大，这种影响逐渐减小，而1×1×2的模型的晶格常数a出现增大的现象则是由于空位位置对于结构的不对称性造成的.

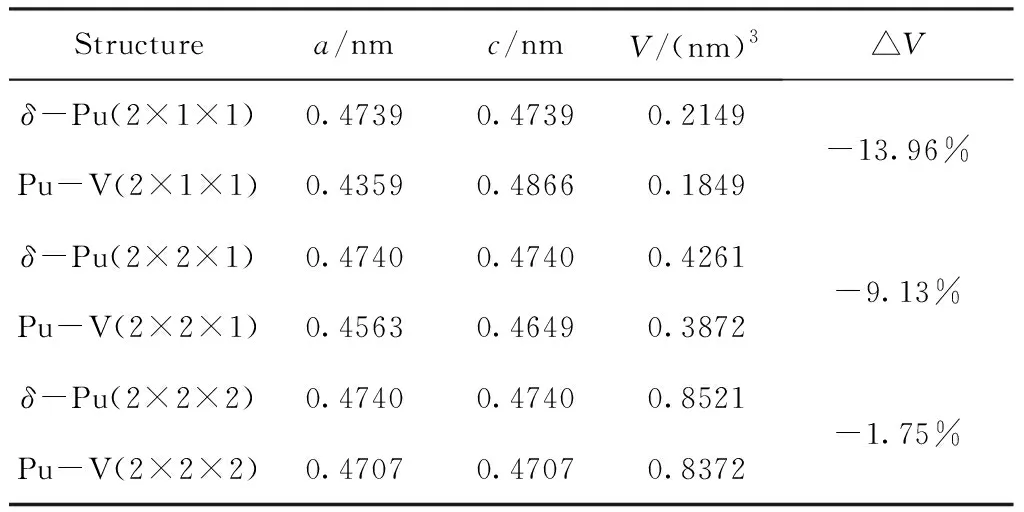
表1 不同超胞的结构参数

空位形成能反映了空位形成的难易程度，形成能越小表明空位越容易形成，空位形成能的计算式为[22]：

Ev=Edef+nμPu-Epure

(1)

式中EV为空位形成能，Edef为含缺陷的超胞总能，Epure为等大不含缺陷超胞总能，μPu为Pu原子的化学势，即理想晶胞中每个Pu原子的能量，n为空位的数量. 空位形成能的计算结果如表2所示. 从表中可以看出，三种模型中的空位形成能均为正，表明空位形成过成中需要吸收热量，这也说明空位是不稳定的，而实际上在δ-Pu中，辐照损伤和退火是同时进行的，辐照损伤产生的自间隙原子会迅速与空位结合[23]. 而在3种空位模型中，空位浓度为6.25%(2×2×1)的模型空位形成能最小，表明此时的空位最容易形成，其次为空位浓度为12.5%和3.125%的模型.

晶体结合能定义为将自由的原子、离子或分子结合成晶体时释放的能量，结合能数值越大，则晶体的结构越稳定. 本文中晶体原子的平均结合能可按式(2)进行计算[24]：

(2)

式中Ecoh为晶体原子平均结合能，Eatom为Pu原子的自由能，Etot为晶体的总能量，n为晶体的原子总数. 采用建立一定大小的晶胞，并在中心添加一个Pu原子的方法计算Pu原子的自由能，经计算可知，当晶格常数大于2nm后，其能量趋于恒定，可以将此时的能量取为Pu原子的自由能. 结合能的计算结果列于表2. 从表中可以看出，对于不含空位的模型，计算的结合能数值是一样的，而含空位的模型的结合能均低于不含缺陷的模型，表明其放热量更少，结构稳定性也更低. 可以看出，在3种空位模型中，空位浓度为6.25%的模型的结合能最大，因而其结构稳定型也最好，其次为空位浓度为3.125%和12.5%的模型.

表2 不同超胞的空位形成能和结合能

Table 2 Vacancy formation energies and cohesive energies of different supercells

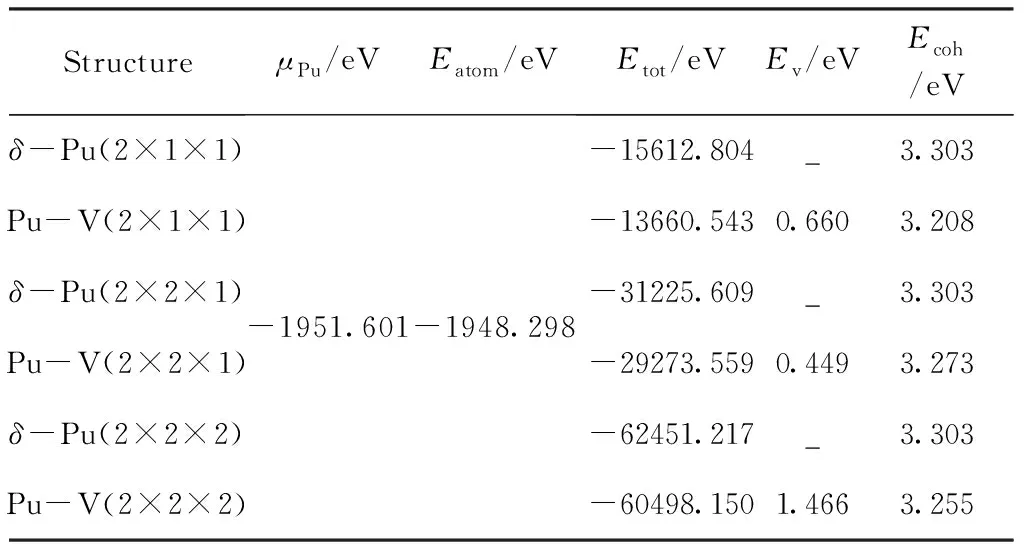
StructureμPu/eVEatom/eVEtot/eVEv/eVEcoh/eVδ-Pu(2×1×1)Pu-V(2×1×1)δ-Pu(2×2×1)Pu-V(2×2×1)δ-Pu(2×2×2)Pu-V(2×2×2)-1951.601-1948.298-15612.804_3.303-13660.5430.6603.208-31225.609_3.303-29273.5590.4493.273-62451.217_3.303-60498.1501.4663.255

3.2 空位对δ-Pu电子结构的影响

3.2.1态密度和分态密度

结构和稳定性分析的结果表明，空位在δ-Pu中不能稳定存在，且其稳定性和空位浓度密切相关. 为了进一步分析空位对δ-Pu电子结构的影响，本文对含空位和不含空位模型的态密度、分态密度、电荷密度以及Mulliken电荷布居进行了计算.

图2所示为含空位和不含空位模型的态密度，从图中可以看出，态密度曲线跨过费米能级，表明所有体系均呈现明显的金属性. 还可看出，在费米能级处存在很大尖峰，表明这部分电子的局域性很强. 对比各态密度图可知，尽管空位没有在禁带处引入缺陷能级，但也使态密度曲线发生明显变化，可以看出随空位浓度增大，态密度曲线呈现出低缓的趋势，表明电子局域性逐渐降低. 此外，由于材料的导电性能主要与费米能级附近的态密度峰有关，所以随空位浓度的增大，材料的导电性能也逐渐下降.

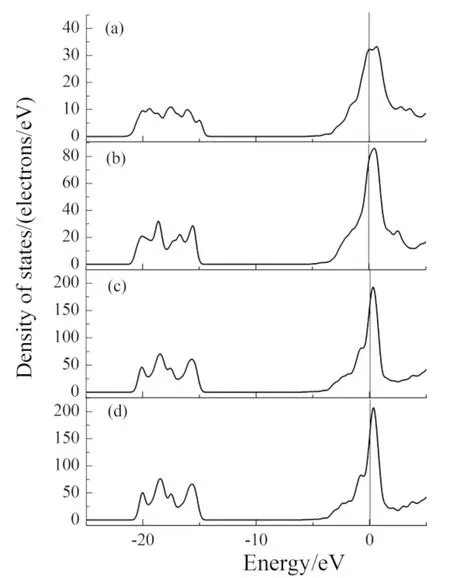
图2 不同超胞的总态密度Fig. 2 TDOSs of different supercells(a)Pu-V(1×1×2);(b)Pu-V(2×2×1); (c)Pu-V(2×2×2); (d)δ-Pu(2×2×2)

图3为含空位模型中空位的第一邻近Pu原子以及不含空位模型中Pu原子的分态密度，图4为图3的局部放大图. 由图3可知，费米能级处的态密度峰主要由5f电子贡献，表明δ-Pu的性质与5f电子密切相关，且费米能级处的5f电子具有很强的局域性；空位对各轨道电子产生了明显的影响，随着空位浓度的增加，6p、6d电子的态密度曲线逐渐平缓，5f电子态密度峰高度降低，宽度增加，其中从图3(a)中还可以看出，6p电子的态密度区域向两侧明显展宽，5f电子的态密度峰在晶体场的作用下产生分裂，形成了两个态密度峰.

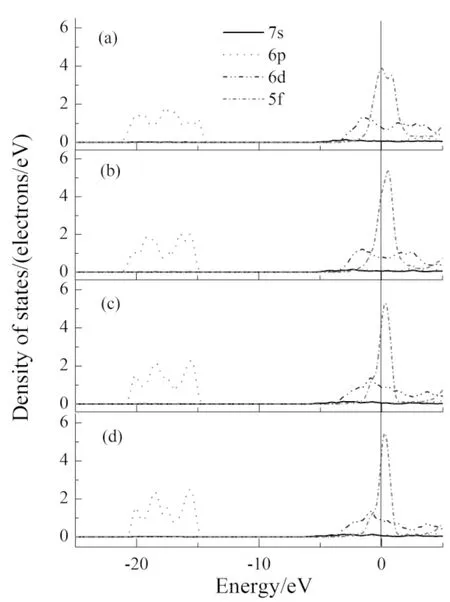
图3 不同超胞中原子的分态密度Fig. 3 PDOSs of atoms in different supercells(a)Pu-V(1×1×2);(b)Pu-V(2×2×1);(c)Pu-V(2×2×2); (d)δ-Pu(2×2×2)

从图4中可以看出，7s和6p电子存在一定程度的sp杂化，而且空位对于各模型中最邻近Pu原子的7s和6p电子的影响存在较大差异，其中对空位2×2×2的模型最邻近原子的态密度影响较小，对2×2×1和1×1×2的模型的最邻近原子的态密度影响则比较显著. 另外一个有趣的现象是，在2×2×1的模型中，7s和6p电子在0～4 eV的区域内出现了明显的“共振”，表明它们发生了较强的杂化作用，然而类似的现象在其它两个空位模型中并没有出现，这在一定程度上解释了前文2×2×1的空位模型的稳定性强于其他两个模型的计算结果.

3.2.2电荷密度和Mulliken布居分析

为进一步了解空位对原子的成键以及电荷的分布和转移情况的影响，本文计算了含空位模型(2×2×2)和不含空位模型的电荷密度分布，并进行了Mulliken布居分析. 图5为不含空位模型和含空位模型的电荷密度分布图. 从图中可以看出，在两种模型中，Pu原子周围均存在大量电荷，且总体上呈球对称分布，邻近原子之间的电荷密度较小，没有明显的相互作用，体现了明显的金属键特征. 但是空位也导致电荷的密度分布发生了变化，对比图5(a)和图5(b)可知，相对于不含空位的模型，含空位模型中的Pu原子与空位邻近的区域电荷密度有所降低，而与其它钚原子邻近的区域电荷密度有所升高，这是由于Pu原子的缺失，导致电子受力不平衡而引起电荷的重新分布.

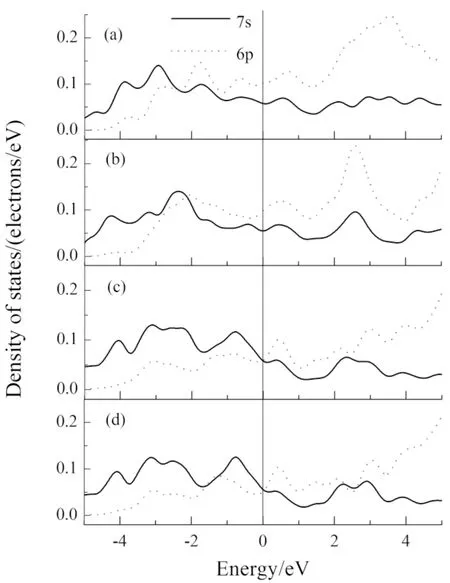
图4 不同超胞中原子的分态密度局部放大图Fig.4 Partially magnified PDOSs of atoms in different supercells(a)Pu-V(1×1×2); (b)Pu-V(2×2×1);(c)Pu-V(2×2×2); (d)δ-Pu(2×2×2)

为了对原子轨道电子的转移和Pu原子的成键情况进行定量化描述，本文计算了不含空位模型的Pu原子以及含空位模型中与空位最邻近的Pu原子的电荷布居以及Pu原子之间的键布居，计算结果列于表3. 由表3可知，所有模型中Pu原子之间的键布居值都为零，表明尽管空位对原子之间的相互作用产生了一定影响，但Pu原子之间仍然保持为完美的金属键；与空位最邻近的Pu原子均失去部分电子而带正电，且失去的电子主要由6p轨道贡献. 可以看出，2×2×1和2×2×2的模型中的Pu原子失去电子数多于1×1×2的模型中的Pu原子，这主要是因为其周围的Pu原子数更多. 空位也对Pu的轨道电子分布产生了一定影响，且空位浓度越大，这种影响越显著，其中从1×1×2的模型中可以明显看出，部分6p电子向7s和6d轨道发生转移，而且5f电子由于局域性降低，也向6d电子发生了部分转移.

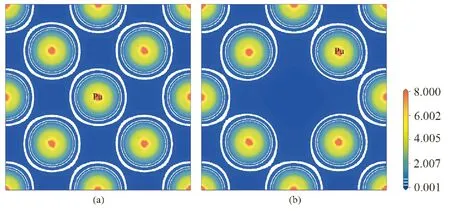
图5 不含空位超胞和含空位超胞的电荷密度Fig. 5 Electron densities of supercells with and without vacancy(a) δ-Pu(2×2×2); (b) Pu-V(2×2×2)

4 结 论

(1)空位导致模型的晶格常数和体积减小，且空位浓度越大，减小的幅度也越大；3种缺陷模型中，空位的形成能均为正，其中2×2×1的模型的空位形成能最小，表明空位在δ-Pu中不稳定，但在2×2×1的模型中空位的稳定性相对更强；空位使得δ-Pu晶体的结合能降低，结构稳定性也降低，其中2×2×1的空位模型的结构稳定性也相对更强.

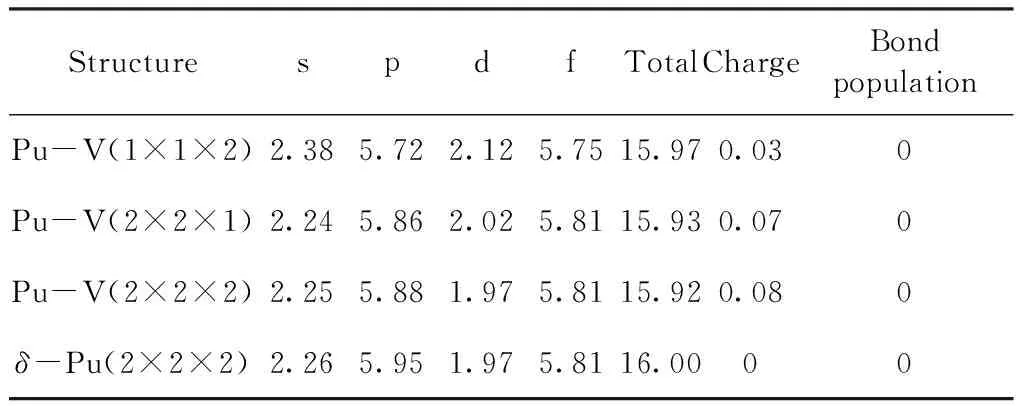
表3 不同超胞中原子的Mulliken布居分析

(2)随空位浓度的增加，主要的态密度曲线呈现出低缓的趋势，电子的局域性降低；Pu原子的7s和6p电子存在一定程度的sp杂化，且在2×2×1的空位模型中sp杂化明显增强，这在一定程度上解释了其结构稳定性强于另外两种空位模型的现象；在空位模型中，Pu原子之间仍保持为完美金属键，但空位引起了Pu外层电子由近空位端相向近Pu原子端转移，并导致与其最邻近的Pu原子失去电子，而失去的电子主要由6p轨道贡献.