中空结构Pt纳米粒子热稳定性和形变的分子动力学研究
2019-04-28李榜全卢玉和陈爱军崔益民
李榜全,卢玉和,陈爱军,崔益民
(1. 山西大同大学 物理与电子科学学院, 大同 037009; 2. 北京航空航天大学 物理与核能工程学院, 北京 100083)
1 引 言
燃料电池能量转换效率高、燃料来源可持续、工作温度低和污染物排放少,在运输和转换能源方面有着广阔的应用前景[1-3]. 金属Pt作为催化剂,具有优异的催化性能,广泛应用于燃料电池. 随着纳米合成和燃料电池技术的发展,合成尺寸和形貌可控的Pt纳米粒子(NPs)受到广泛的关注[4]. 中空结构纳米粒子在保持结构稳定性的情况下,密度低、成本低、比表面积大,可以提高Pt的利用率. 实验上通常可以利用模板法合成具有高比表面积和体积比的中空结构Pt纳米粒子,以便更多的金属原子在粒子的表面和接近反应物分子[5, 6]. 纳米粒子的形貌、晶体结构和组份的设计有助于提高催化的选择性和活性,在加热和外部施加压力条件下,研究纳米材料的热力学稳定性和动力学过程成为研究热点[7, 8]. 分子动力学是研究原子和分子物理运动的方法,通过计算机模拟原子和分子相互作用的运动过程,可以直接得到系统的结构演化和动力学特性,解释相关的物理机理,并预测新性能、新现象[9-11]. 分子动力学方法研究中空结构纳米粒子结构演化过程,可以发现纳米粒子结构稳定性与壳层厚度的相关性,壳层厚度对纳米粒子熔化模式的影响,以及原子位移对其形貌的作用[12-15].
我们利用分子动力学方法对中空结构Pt纳米粒子的结构稳定性进行模拟分析,比较了不同壳层厚度的纳米粒子的稳定性,分析了不同温度条件下,纳米粒子的形貌变化和原子扩散过程. 这些结果将对中空结构金属纳米粒子的设计和制备,发展具有高催化活性和稳定性的金属纳米晶体提供有意义的理论指导.
2 模型与方法
2.1 模 型
如图1所示,中空Pt纳米粒子初始模型建立过程:首先以Pt的晶格常数3.92 Å建立半径为3.5 nm的球形纳米粒子,然后从球形的中心移除半径分别为0.5 nm、1.0 nm、1.5 nm、2.0 nm、2.5 nm、3.0 nm球形结构,从而形成中空结构,为了方便比较,我们也研究了实心结构的Pt纳米粒子. 选取七种不同的壳层厚度的中空结构纳米粒子进行对比研究,这七种壳层厚度分别命名为HPt1(0 nm)、HPt2(0.5 nm)、HPt3(1.0 nm)、HPt4(1.5 nm)、HPt5(2.0 nm)、HPt6(2.5 nm)、HPt7(3.0 nm).
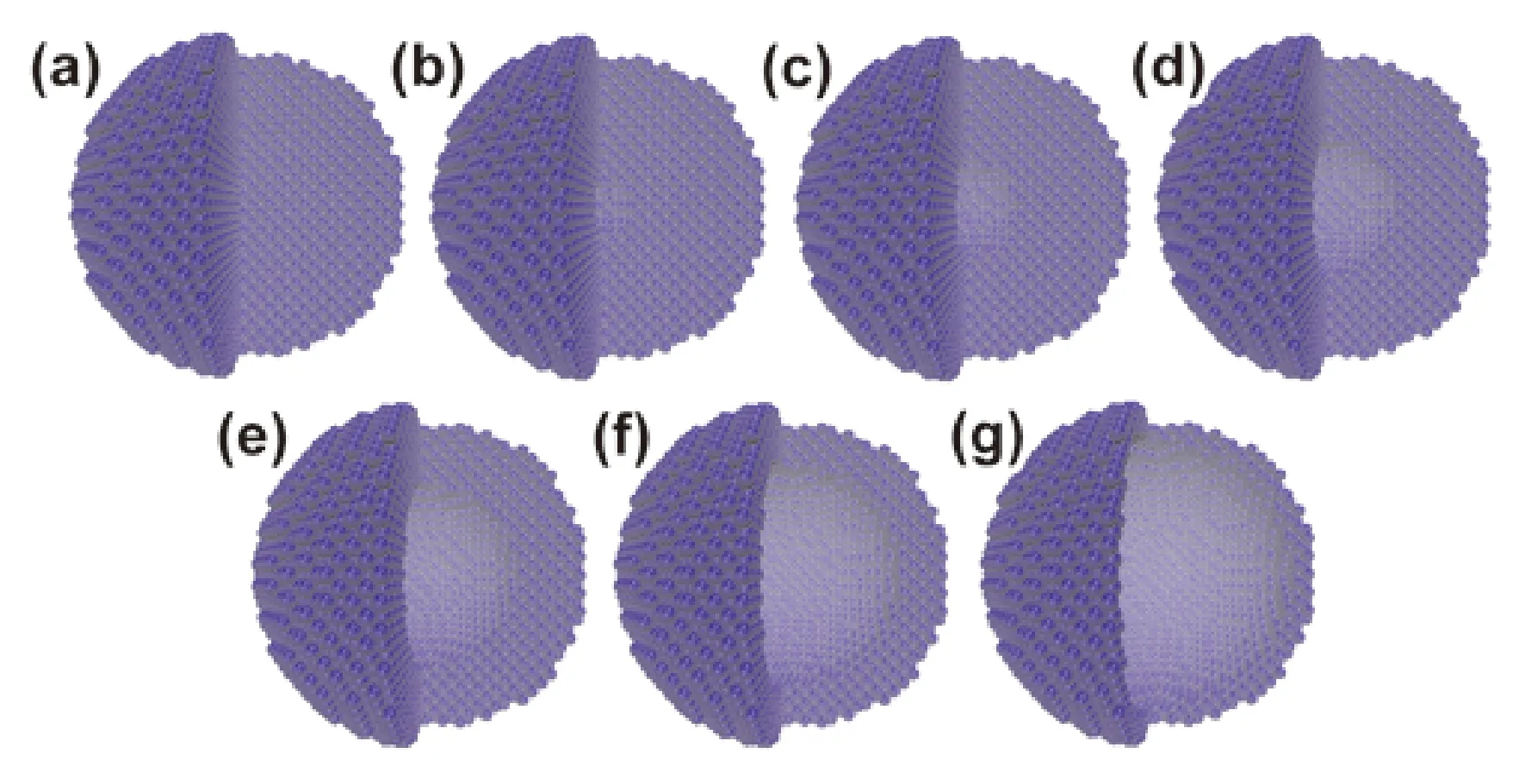
图1 不同壳层厚度的中空结构Pt纳米粒子结构模型 (a) HPt1、(b) HPt2、(c) HPt3、(d) HPt4、(e) HPt5、(f) HPt6、(g) HPt7Fig. 1 Initial configurations of hollow Pt NPs with different shell thickness, (a) HPt1、(b) HPt2、(c) HPt3、(d) HPt4、(e) HPt5、(f) HPt6、(g) HPt7.
2.2 方 法
分子动力学模拟采用Large-scale Atomic/Molecular Massively Parallel Simulator(LAMMPS)软件[16],系综采用正则系综(NVT),模拟过程利用Nose-Hoover控制温度,运动方程步长时间为0.001 ps,积分方法采用velocity-Verlet算法. 首先,纳米粒子在0.1 K下弛豫,直到系统达到稳定状态,然后温度从0.1 K上升到2100 K,升温速率为0.2 K/ps,在2100 K持续300 ps弛豫,这个温度远远高于Pt纳米粒子的熔点,这样保证纳米粒子完全熔化,获得统计数据. 原子间相互作用采用嵌入原子法的力场,该方法为金属元素的晶格常数、空位形成能和弹性模量等的计算提供了合理近似的相互作用[17]. 所采用的作用势在模拟金属纳米材料的结构稳定性和相变过程中得到了较好的效果[18, 19].
3 模拟结果与讨论
势能曲线的变化可以反映出材料的稳定性,由于表面效应,随着纳米粒子尺寸的减小,纳米粒子的晶格常数将减小,通过较长时间的弛豫,纳米粒子趋于稳定结构[20, 21]. 如图2(a)所示,弛豫开始,所有纳米粒子势能降低,然后达到稳定状态. 纳米粒子初始状态的势能较高是由于初始模型的结构由块体材料的晶格常数建立,随着材料的尺寸减小,纳米粒子的晶格常数减小[22]. 随着弛豫过程的进行,从HPt1-HPt6的纳米粒子势能没有明显变化,说明这些空心结构能够保持稳定,而对于HPt7,由于壳层厚度减小,纳米粒子的结构塌缩,体系的势能降低. 利用均方位移(MSD)可以说明原子的位移情形,并解释势能曲线变化产生的原因. 由于原子的热运动,原子可能偏离其理想晶格位置[23]. 当温度较低时,原子停留在振动状态,MSD不会随着时间的推移而改变;当纳米粒子结构发生变化时,原子振动加剧,MSD将发生变化. 由图2(b)可以发现HPt1-HPt6的纳米粒子MSD没有明显变化,而对于HPt7,MSD变化随着弛豫进行,急剧增加,这和纳米粒子结构塌缩相一致.

图2 弛豫过程 (a) HPt1-HPt7纳米粒子的势能的变化图; (b) HPt1-HPt7纳米粒子的MSD的变化图Fig. 2 (a)The potential energy variation and (b) MSD of hollow Pt NPs during the relaxation processes for HPt1-HPt7.
为了分析Pt纳米粒子的稳定性和结构变化,图3给出了势能随温度变化的曲线. 金属纳米材料的势能曲线由于尺寸效应而不同于块体材料. 在熔点处曲线的转变不再是尖锐的,而是在一定的温度范围内发生熔化过程,相应的曲线要变得更平滑[24, 25]. 熔点对应曲线中发生跳跃的温度,能量的突然增加说明了从固态向液态转变的一级相变的发生[26]. 图3(a)给出HPt1和HPt2的势能曲线变化类似于非中空结构纳米粒子的变化过程[27],而图3(a)插图以及图3(b)说明HPt3-HPt7,势能随着温度升高,首先急剧下降,随着温度的进一步升高,发生固-液相变过程,直到粒子完全熔化. 在此过程中,势能随温度的升高而降低的现象,这是由于中空结构纳米粒子发生塌缩,Pt中空结构纳米粒子比表面积减小从而引起能量降低. 这里存在一个竞争关系,即Pt纳米粒子塌缩引起体系的能量降低,同时温度的升高使体系的能量增加. 在这样的竞争关系作用下,对于HPt2,虽然中空结构也发生了塌缩,势能并没有明显降低.

图3 中空结构纳米粒子势能随温度变化曲线 (a) HPt1-HPt4;(b) HPt5-HPt7Fig. 3 Variation of potential energy as function of temperature for hollow Pt NPs (a) HPt1-HPt4;(b) HPt5-HPt7.
在持续加热过程中,为了获得中空结构纳米粒子中原子扩散的直观尺寸变化,引入统计半径的概念[28]. 从图4(a)给出中空结构纳米粒子弛豫过程的统计半径的变化,可以看出纳米粒子HPt1-HPt6的半径除了弛豫开始阶段略有减小外,几乎不变,HPt7的半径急剧减小,这和弛豫过程纳米粒子的势能变化相对应. 图4(b)和(c)分别为HPt6弛豫前后纳米粒子形貌变化,图4(d)和(e)分别为HPt7弛豫前后纳米粒子形貌变化,可以看出HPt6的形貌几乎不变,而HPt7发生明显塌缩. 半径为3.5 nm的Pt中空结构,当壳层厚度为0.5 nm时,在0.1 K的温度条件下不稳定,统计半径的结果和势能变化结论相一致,说明可以利用统计半径表征纳米粒子结构的转变过程.
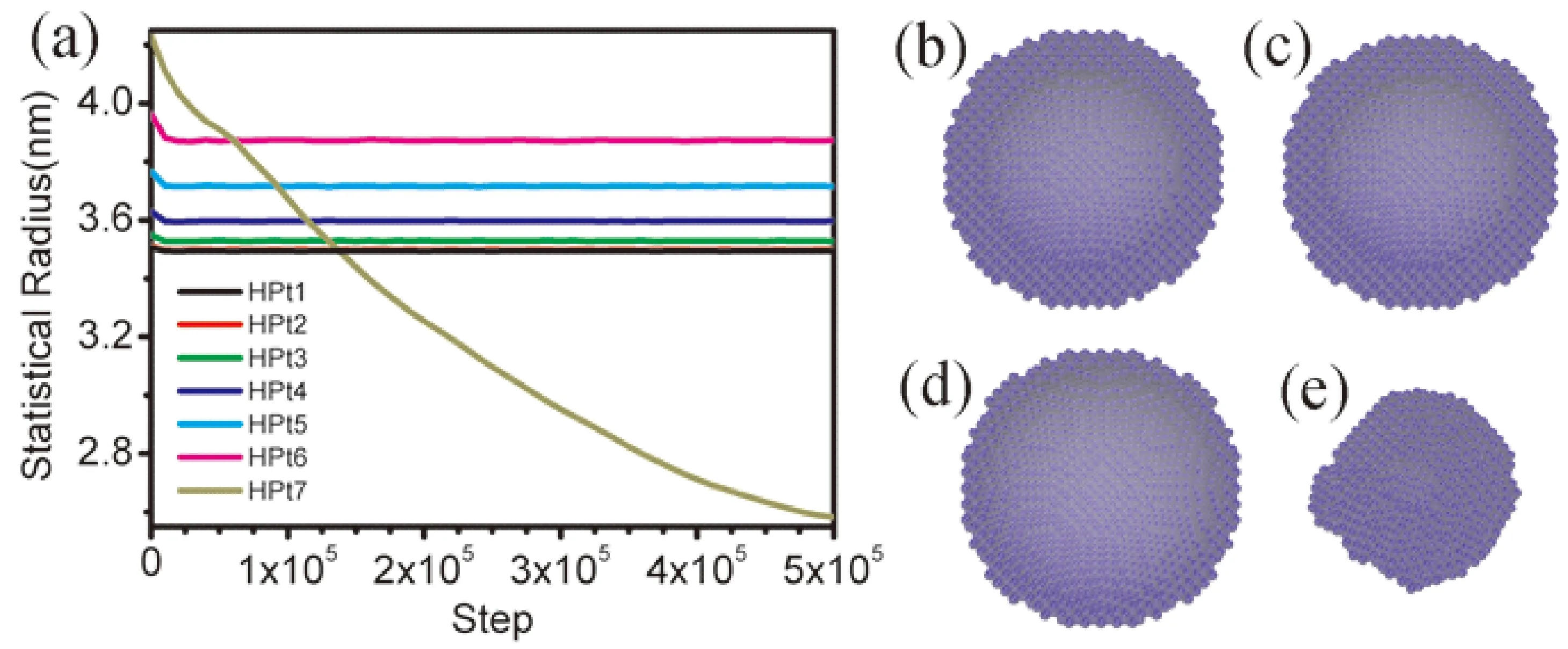
图4 (a)弛豫过程,纳米粒子半径随步数变化曲线;(b)和(c)弛豫前后HPt6纳米粒子剖面图;(d)和(e)弛豫前后HPt7纳米粒子的剖面图Fig. 4 (a) The stepdependence of statistical radius of hollow Pt NPs during relaxation processes; (b) and (c) corresponding to the snapshots of cross sections of HPt6 before and after relaxation; (d) and (e) corresponding to the snapshots of cross sections of HPt7 before and after relaxation.
从图5(a)可以看出:中空结构纳米粒子HPt1-HPt4的半径随温度的升高而缓慢增大,这主要是由晶格常数的热膨胀引起的;随着温度的进一步升高,HPt3和HPt4的统计半径急剧减小,说明中空结构纳米粒子发生了塌缩,这和纳米粒子势能变化趋势相同,也就是说纳米粒子塌缩后的势能减小. 从图5(b)可以发现纳米粒子HPt5和HPt6,随着体系温度的升高,在半径急剧减小前,纳米粒子的半径几乎不变,说明由于热膨胀引起的半径增加值和塌缩引起的半径减小相当. 纳米粒子HPt7在弛豫过程结构发生塌缩,随着温度的升高,半径进一步减小,然后又缓慢升高. 从图5的半径变化过程还可以发现结构塌缩后的纳米粒子,当温度达到熔点时候,半径发生跳跃变化,说明纳米粒子发生了从固态到液态的转变,这和势能变化过程相对应,还可以看出纳米粒子塌缩几乎在某个温度点发生,也就是说塌缩的温度区间很窄.

图5 (a)HPt1-HPt4和(b)HPt5-HPt7纳米粒子半径随温度变化曲线Fig. 5 Temperature dependence of statistical radius of hollow Pt NPs, (a) HPt1-HPt4 and (b) HPt5-HPt7.

图6 纳米粒子在塌缩温度点的形貌图(上)和剖面图(下),(a)-(g)分别对应HPt1-HPt7Fig. 6 Snapshots of morphology (up) and cross-section (down) at different collapse temperature,(a)-(g) corresponding to HPt1-HPt7, respectively.
为了进一步分析纳米粒子塌缩后内部结构变化,我们分别选取HPt1-HPt7塌缩后,但结构未熔化时粒子的形貌图(上)和剖面图(下). 从图6(a)-(g)分别对应HPt1-HPt7纳米粒子的形貌图. 可以看出随着壳层厚度的减小,形貌变化越明显,这和纳米粒子的半径变化相一致,还可以发现纳米粒子塌缩后,Pt纳米粒子中的原子重新排列,仍保持有序结构.
径向分布函数(RDF)的峰位反映了纳米粒子的局域结构,第一个峰位对应最近邻原子距离,第二个峰对应晶格常数[29]. 图7为纳米粒子HPt1-HPt7的径向分布函数(图6温度点),所有的中空结构Pt纳米粒子的fcc结构的特征峰都存在,从第二峰对应的位置可以发现Pt粒子的晶格常数变化不大. 这些结论说明,在结构塌缩过程Pt纳米粒子的晶体结构没有明显变化,保持有序fcc结构,研究发现有序结构能够一直保持到熔化前.

图7 温度为1100 K时,中空Pt纳米粒子的径向分布函数Fig. 7 RDFs of hollow Pt NPs at the 1100 K.
4 结 论
Pt金属纳米粒子作为一种重要的催化剂在电催化等催化体系中有着重要的应用,利用分子动力学方法对中空结构纳米粒子的形变过程进行研究发现:半径为3.5 nm的中空结构Pt纳米粒子的壳层厚度为0.5 nm时并不稳定,在0.1 K弛豫过程会发生塌缩;随着壳层厚度增加,纳米粒子塌缩时对应的温度越高,且所有纳米粒子结构塌缩过程都经历较短时间或者较小温度范围,最终转变为实心结构;另外还发现纳米粒子塌缩后内部结构仍保持有序fcc结构. 中空结构纳米粒子结构稳定性以及形变过程的研究将为金属纳米粒子的组份设计和性能调控提供理论指导.
