椭圆中的切线方程及其应用

浙江省诸暨市第二高级中学 (311800)

朱水英

切线问题是高中数学的常见问题，如何求切线方程则是解决问题的关键.函数的切线方程一般采用导数的几何意义求解，而圆锥曲线的切线方程一般采用直线与圆锥曲线方程组联立，消x或y，得到一个一元二次方程，直线与圆锥曲线相切，即方程只有一个实数解，利用判别式Δ=0求解，即判别式法，这也是圆锥曲线中求切线方程的通法，但是此法计算量较大.

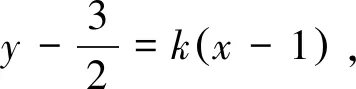
此法就是判别式法的运用，但是计算较大，对很多学生来说可能会出现一种普遍现象：会做但算不对.下面介绍椭圆的切线方程，首先引导学生从导数角度入手自己动手推导椭圆在其上一点处的切线方程.

一、推导切线方程

图1

图2

评注：此法是运用了导数的几何意义进行推导，当然也能用判别式法，但是计算量较大，本文就不做介绍了.对公式推导是为了让学生在运用公式前能知其所以然，运用已有的导数知识来解决圆锥曲线问题，看似两块不同的章节，但也能有相通的地方，能让学生感知数学知识的相互关联性，在以后的学习中能开阔思路，提升学习能力.

二、强化切线应用

图3

分析：此题考查直线与圆锥曲线的位置关系，只有一个公共点即直线与椭圆相切，一般采用判别式法，参考答案也是采用此法，但是计算量大，尤其是带有三个字母，正确率就更低了，而且还影响了下一小题的解答，因此当年此题的得分比较低.

以下运用椭圆的切线方程解答：

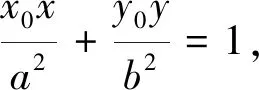
图4

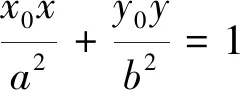
三、推广曲线切线

圆锥曲线教学中，椭圆、双曲线、抛物线有类似的解题思路，是否在切线方程求解上有类似的公式？作为一名高中数学教师不仅要教会学生如何解题，更要教会学生解题的思想方法，这样才能让学生举一反三，提高学习的效率.自己动手，丰衣足食.

(2)点P(x0,y0)为抛物线C:x2=2py上任意一点，则抛物线C在点P之处的切线方程为x0x=p(y0+y).

(3)点P(x0,y0)为抛物线C:y2=2px上任意一点，则抛物线C在点P之处的切线方程为y0x=p(x0+x).

(4)点P(x0,y0)为圆C:x2+y2=r2上任意一点，则圆C在点P之处的切线方程为x0x+y0y=r2.

数学注重对学生核心素养的培养，这是学生受用一生的能力.推理和运算是思维训练的载体，逻辑推理和数学运算都是中学数学的核心素养，能对所学的知识学以致用，推理出一个新的结论，这也是一种能力的体现.就如本文用导数的思想推导了圆锥曲线的切线方程，就是让学生体会函数思想是高中数学的基本思想，数学内容是相互串联的，它们是自成一体的.而数学运算能力是思维能力和运算能力的结合，高考对运算求解能力的考察重点放在算理的应用、运算途径的判断、运算方法的选择上，这也是考察学生的综合能力，所以在解析几何教学中，运用一些必要的结论与公式来简化运算，提升学生解题的信心，是很有必要的一种手段.增强求简意识，也是我们数学教学和高考复习中必须遵循的.