矩形断面二维浅埋硐室顶部双层围岩塌落面上限分析
2019-04-26曾中林李亮刘双墉左学贤
曾中林,李亮,刘双墉,左学贤
矩形断面二维浅埋硐室顶部双层围岩塌落面上限分析
曾中林,李亮,刘双墉,左学贤
(中南大学 土木工程学院,湖南 长沙 410075)
基于极限分析上限定理和Hoek-Brown破坏准则,构建了浅埋矩形硐室双层围岩塌落破坏机制,并根据虚功原理获得了一个围岩塌落形态方程的泛函。利用变分法得到极限状态下围岩塌落破坏曲线函数,并根据边界条件得到待定系数,进而得到围岩塌落破坏曲线的解析式。当双层围岩退化为单层围岩时,与已有研究成果完全一致,可以证明本文分析模型的正确性。在此基础上,分析了各参数对浅埋隧道双层围岩塌落破坏形状的影响规律,可为浅埋硐室顶部双层围岩潜在塌落范围的预测提供理论依据。
塌落稳定性;双层围岩;浅埋硐室;Hoek-Brown破坏准则;极限变分分析
近年来,随着中国城市化进程的加速,城市建设用地越来越紧张。为了解决这一问题,地下空间的开发与利用得到广泛重视,越来越多的浅埋地下建筑也出现在市政建设中。由于这些浅埋地下结构上部覆盖的岩土层较薄,在开挖过程中易出现由支护措施不当导致的地表塌陷,因而浅埋洞室的稳定性问题得到相关领域研究人员的极大关注。张成平等[1−2]结合理论分析和模型试验方法,通过对浅埋暗挖隧道施工引起的地表塌陷进行深入分析,揭示了地表塌陷的发生机理,并结合地层条件和施工情况得出诱发地表塌陷的原因。在现有多数关于隧道稳定性研究中,大都采用适用于土体抗剪强度的Mohr-Coulomb屈服准则,但对于内部存在很多节理和结构面的岩体,Mohr-Coulomb准则很难准确地描述其破坏特征。鉴于Hoek-Brown屈服准则能够反映岩石强度、结构面组数、所处应力状态对岩体强度的影响[3−4],因此在岩土构筑物稳定性分析中得到广泛运用[5−6]。在隧道或硐室围岩塌落稳定性分析方面:Fraldi等[7−8]基于Hoek-Brown破坏准则推导出二维深埋隧道的塌落形状表达式,并进行隧道渐进式塌落破坏的理论研究;HUANG等[9−10]根据岩体Hoek-Brown破坏准则,分析孔隙水压力,分别讨论浅埋圆形硐室支护前后的塌落机制。QIN等[11−12]考虑岩层发生风化等参数弱化情况,进一步探讨深埋隧道进一步塌落机制。延续Fraldi等[7−8]的研究成果,近年来,对有深、浅埋硐室围岩塌落稳定性研究仍有拓展研究[13−16]。然而,上述研究都是针对均质单一岩层的硐室围岩开展,而实际工程中由于地质沉积或差异风化等原因,岩体分层的情况非常常见。特别是对于浅埋隧道而言,岩体分层对其塌落稳定性影响更为强烈,因此,有必要对于分层围岩中浅埋硐室稳定性进行进一步深入研究。本文主要针对具有双层不同岩体属性的浅埋洞室开展稳定性研究,研究对象是对于已有硐室塌落稳定性研究的延伸和扩展。在考虑浅埋硐室顶部围岩分层的情况下,构建一种浅埋硐室顶部围岩的二维破坏机制;根据极限分析上限定理中内能耗散功率和外力功率计算,得到包含上下围岩二维破坏面方程的目标函数;并利用变分法推导出浅埋硐室顶部双层围岩塌落体曲面方程的上限解,以期为分层围岩中浅埋硐室顶部围岩潜在塌方范围的预测提供理论依据。
1 Hoek-Brown非线性破坏准则
Hoek-Brown破坏准则能够有效全面、具体地描述岩体的非线性破坏特性,能够更好地阐述岩体的破坏规律,Hoek-Brown破坏准则可以用最大主应力和最小主应力表示为[15]:

式中:1为最大有效主应力;3为最小有效主应力;ci为岩体单轴抗压强度;m,和是无量纲参数。
另一方面,Hoek-Brown破坏准则也可由法向应力和切向应力表达[16]:

式中:n为有效主应力;为切向应力;和均为材料参数;ci为岩体的单轴抗压强度;tm为岩体抗拉强度。
2 双层围岩塌落破坏上限分析
2.1 双层围岩塌落破坏机制
对二维浅埋硐室稳定性的研究,均基于同种围岩,而在实际工程中,浅埋硐室的围岩不仅仅只是某种单一岩层,很可能出现几种不同强度围岩的情况。考虑到二维浅埋矩形硐室顶部存在双层围岩,构建浅埋硐室顶部双层围岩的塌落破坏机制,如图1所示。矩形硐室顶部上下2层岩体塌落破坏速度间断曲线分别为1()和2(),构成了上窄下宽的倒漏斗形塌落面。1()从岩层分界面延伸到地表,2()从1()与分界面的交点出发延伸到硐室顶部。上层塌落体的上下半宽分别为1和2,下层塌落体的上下半宽分别为2和3,上下2层岩体的厚度分别为1和2。显然,2条曲线在分界面处(即2处)具有连续性。因为存在着2层围岩,所以需要2对相应的强度参数来区分岩体的不同性质。
2.2 双层岩体围岩塌落上限分析
将岩体破坏分离曲面看作具有一定厚度的薄变形层,薄变形层上剪应力与正应力n满足Hoek-Brown破坏准则,根据式(3),屈服函数可表示为

在主应力空间内,令塑形势函数面与强度屈服面重合,根据相关流动法则,可得塑形势函数为:
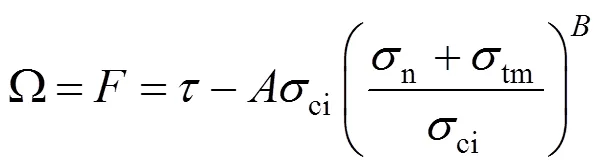
根据塑形位势理论[7],塑性应变率为:
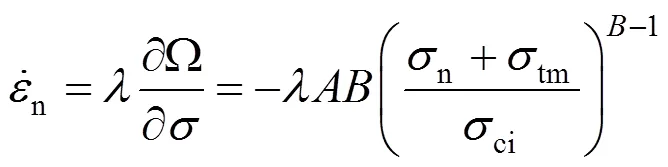

式中:为比例系数。

图1 浅埋矩形硐室顶部双层围岩破坏机制
根据曲线形速度间断线的方程()的斜率′(),采用三角变换可以得到速度间断线上任一点处的法向速度和切向速度,进而得到法向塑性应变率和切向塑性应变率:

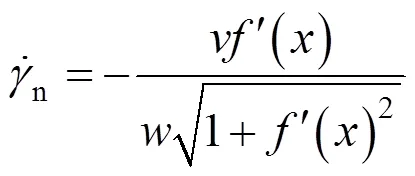
以上式中:为速度间断面的厚度;为刚性冲切体的速率。代入可得速度间断面上法向应力和切向应力为:
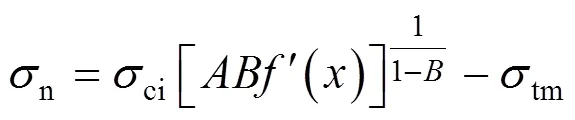

根据Fraldi等[7]的研究,速度间断面上任一点的内能耗散功率可由法向应力和切向应力各自产生的耗散功率叠加得到,即:


又由于上下层岩体参数不同,故整个速度间断线上的耗散功率也由2部分组成,考虑到对称塌落破坏,故取1/2计算:
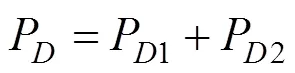
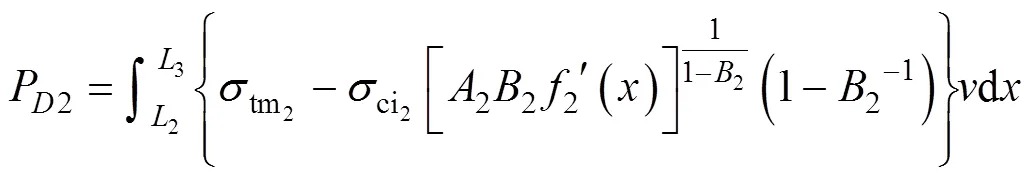
硐室上方塌落体,由于重力作用,产生功率P为:

其中:1和2分别为上下层岩体每单位体积的重度,kN/m3;1和2分别为上层塌落体的上下半宽;2和3分别为下层塌落体的上下半宽;上下2层岩体的深度分别为1和2。显然,对于浅埋矩形硐室的埋深,存在着=1+2。
硐室顶部支护力的功率为:

地表荷载s的功率为:
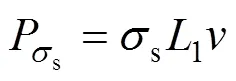
利用内能耗散功率和外功功率之差构造目标函数:
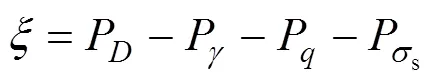
将式(13)~(16)代入式(17),可得浅埋矩形硐室顶部双层围岩情况下,目标函数的具体表达式:



其中:

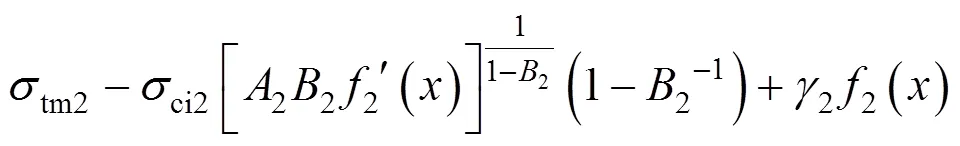
要求的极值,必先求1和2的极值。由于1和2都是泛函,利用变分法的原理,可以解得1′(),1()和2′(),2()的表达式:




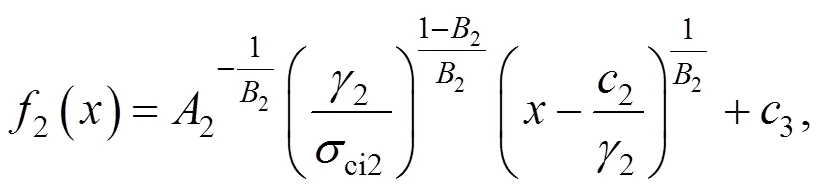

将式(20)~(23)代入式(19),可得:
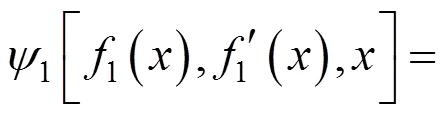
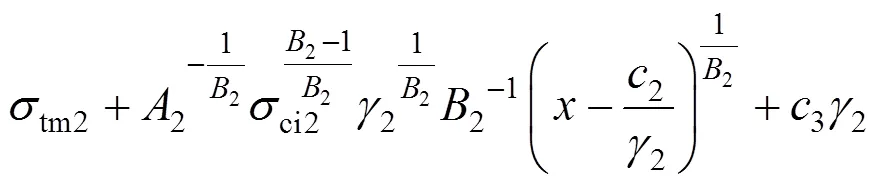
将式(24)代入式(18),有:
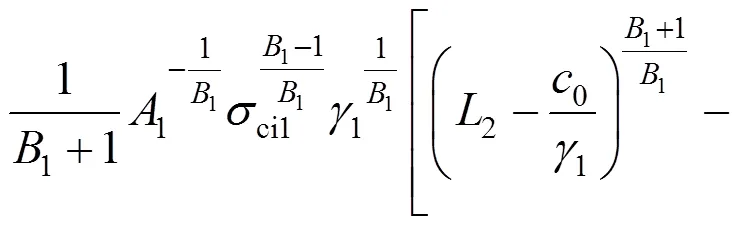
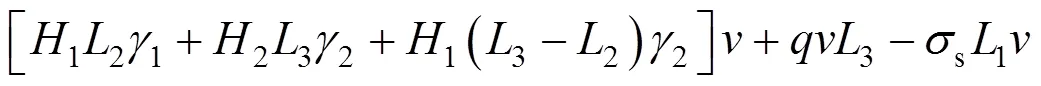
利用地表处无切应力分布,τ为0的边界条件,可以先求得0。

坐标系中(如图1所示),显然有:

将式(27)与式(21)联立求解,可得:

另外一个重要条件,在=2处,1()和2()连续,所以,1()和2()的导数相等,即:
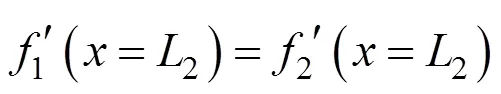
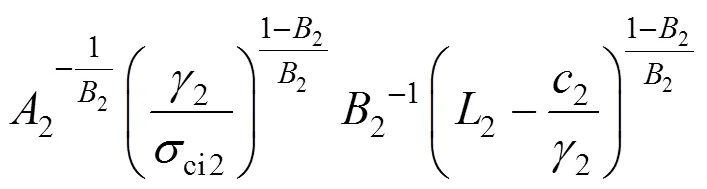
坐标系中存在着以下几何关系:
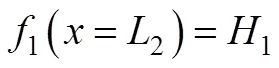

即:


利用上限定理,内能耗散功率和外功功率相等,即目标函数=0,建立方程:


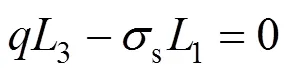
式(30),(32),(33)构成一个非线性方程组,求解这个方程组可以得出1,2,3,2和3的数值解。将1,2,3,2和3的值代入式(21)和式(23),可得速度间断曲线1()和2()的表达式,根据表达式可以绘制二维浅埋矩形硐室在双层围岩条件下的塌落面形状:


2.3 双层岩体围岩退化为单层岩体特例
当上下层岩体参数相同时,退化为均质的单层围岩,此时双层岩体的塌落破坏机制退化为单层围岩的塌落。
由式(11)可得速度间断线上任一点处的内能耗散功率为:

考虑到对称破坏,故取1/2计算。将一点处的内能耗散功率沿整个曲线积分,就可以得到整个曲线上的耗散功率:

1和2分别是()两端的水平投影,即塌落体顶端和底端的半宽度。
硐室上方的塌落体,考虑自身重力作用,产生的功率P为:
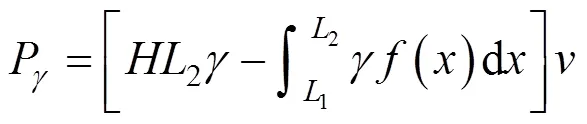
其中:为岩体每单位体积的重度,kN/m3;为浅埋矩形硐室的埋深。
考虑到支护效应,硐室支护力的功率为:

地表荷载s的功率为:
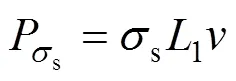
同理,根据内能耗散功率和外功功率之差构造一个目标函数(也称总耗散量):

将式(37)~(40)代入式(41),得到:

其中:
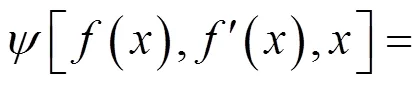

根据变分原理将泛函的极值问题转化为求解欧拉方程在满足边界条件下的定解问题。通过已知的边界条件,可以求得()的表达式,从而使得式(42)的积分成为一个定值。所对应的欧拉方程为:

将式(43)代入式(44),可得:

求解可得:
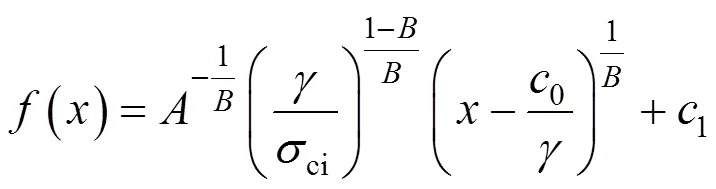
0和1均为积分常数,可以用边界条件求得。

将式(46)代入式(42),可得:
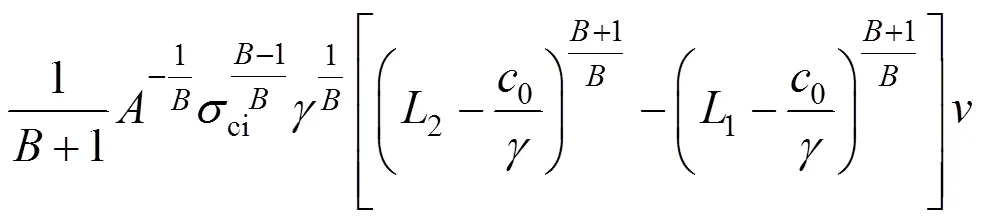
同理,根据式(26)可得
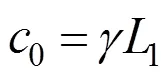
将式(46)与式(48)联立求解,可得:

式(49)中有1和2共2个未知数,单由一个方程是无法解出的。根据外功功率和内能耗散功率相等,可得:

联立式(50)~(51)2个方程组,可以解得1和2的值,再代入式(46),可以得到速度间断线()的表达式,根据表达式可以绘制二维浅埋矩形硐室在单层围岩条件下的塌落面形状:
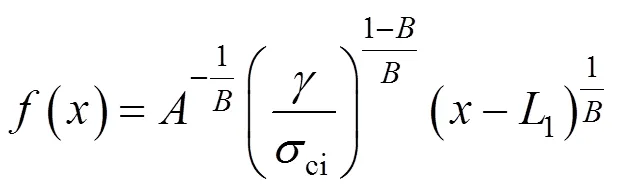
3 数值计算与分析
3.1 对比计算
当上下层岩体参数一致时,退化为单层围岩的塌落,与原有单层围岩的塌落破坏对比。如图2所示,分别对比分析地表破坏宽度1和硐室破坏宽度3。
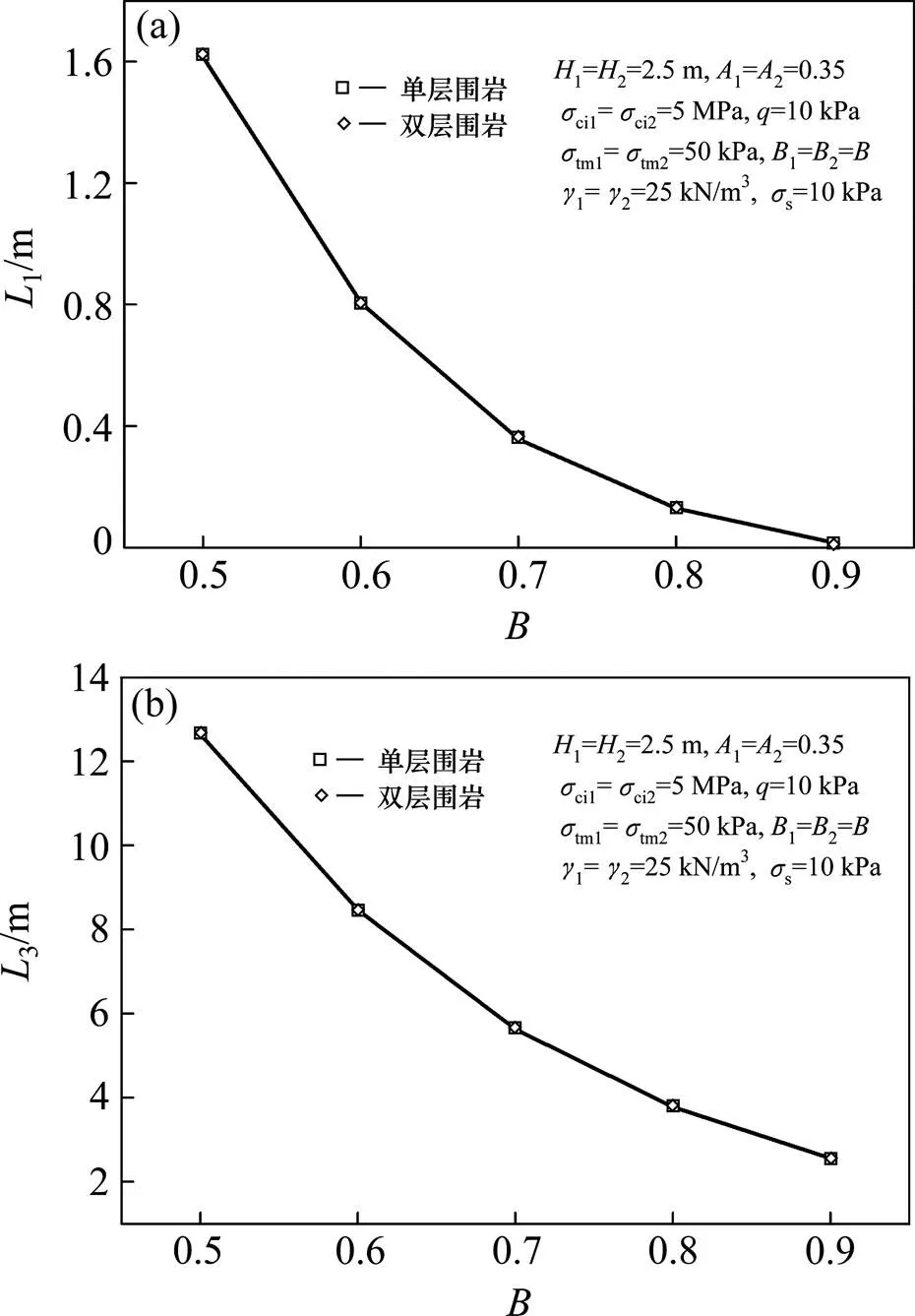
(a) L1比较;(b) L3比较
由图2可知,当双层围岩参数一致时,此时退化为单层围岩的塌落,其塌落范围也与单层围岩一致,因此,当参数一致时,单层围岩的塌落只是双层围岩塌落的一种特殊情况。通过对比,也验证了本文计算双层围岩塌落范围方法的有效性。
3.2 不同参数对浅埋矩形硐室双层围岩塌落面形状的影响
根据式(34)和式(35)得到的塌落面形状表达式,可以分析不同参数对浅埋矩形硐室顶部有双层围岩情况下塌落面形状的影响,由于表达式和双层围岩参数的组合形式过于复杂,为了简化,这里将分析上下层围岩参数的比值对塌落面形状的影响,同样采取控制变量法。
3.2.1 参数1/2比值对硐室塌落面形状的影响
当其余参数为1=2=0.8,ci1=ci2=2.5 MPa,tm1=tm2=ci2/100,1=2=24 kN/m3,1=2=5 m,=15 m,=80 kPa,s=100 kPa,参数1/2=0.3/0.6~ 0.9/0.6变化时,塌落面形状变化情况如图3所示。

图3 参数A1/A2比值影响图
3.2.2 参数1/2比值对硐室塌落面形状的影响
当其余参数为1=2=0.6,ci1=ci2=2.5 MPa,tm1=tm2=ci2/100,1=2=24 kN/m3,1=2=5 m,=15 m,=80 kPa,s=100 kPa,参数1/2=0.6/0.8~ 1.0/0.8变化时,塌落面形状变化情况如图4所示。

图4 参数B1/B2比值影响图
3.2.3 参数1/2比值对硐室塌落面形状的影响
当其余参数为1=2=0.6,1=2=0.8,ci1=ci2= 2.5 MPa,tm1=tm2=ci2/100,1=2=5 m,=15 m,=80 kPa,s=100 kPa,参数1/2=16/20~24/20 kN/m3变化时,塌落面形状变化情况如图5所示。
3.2.4 参数tm1/tm2比值对硐室塌落面形状的影响
当其余参数为1=2=0.6,1=2=0.8,ci1=ci2= 2.5 MPa,1=2=24 kN/m3,1=2=5 m,=15 m,=80 kPa,s=100 kPa,参数tm1/tm2=(ci1/25)/ (ci2/100)~(ci1/400)/(ci2/100)变化时,塌落面形状变化情况如图6所示。同样,因为岩体拉伸强度tm的取值方法,所以tm1/tm2比值对塌落面形状的影响趋势自然就和ci1/ci2比值一致。
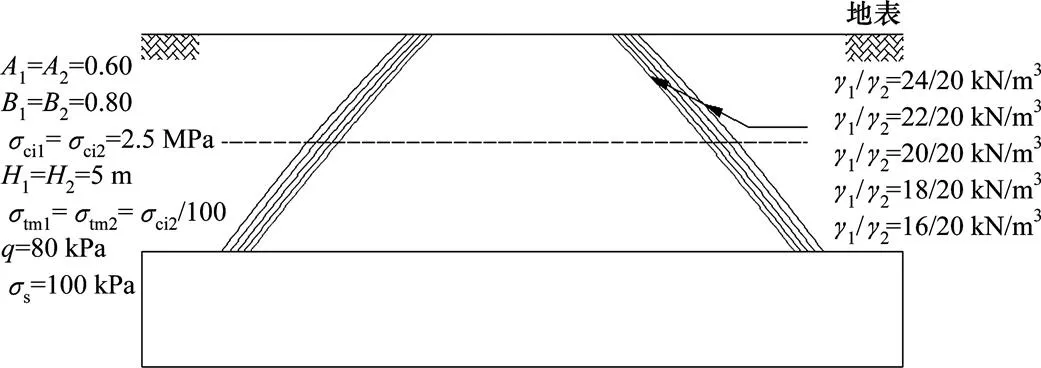
图5 参数γ1/γ2比值影响图
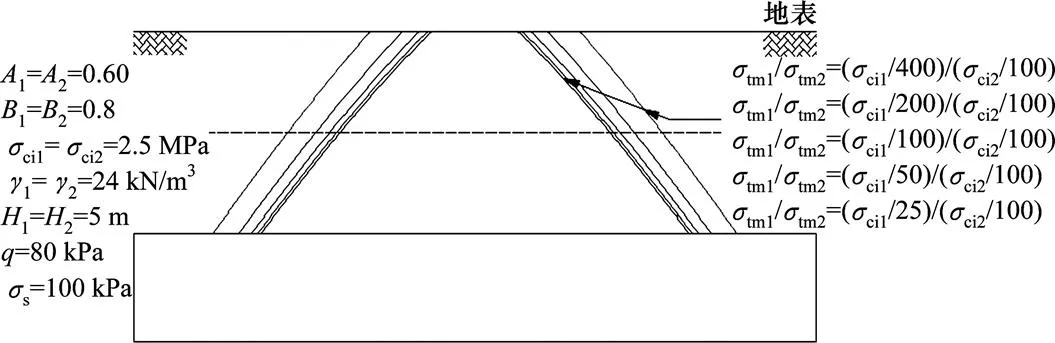
图6 参数σtm1/σtm2比值影响图
通过分析图3~6所描述的二维浅埋矩形硐室顶部有双层围岩情况下的塌落面变化情况,可以得到如下结论:无论参数如何变化,硐室的塌落面都呈抛物线型,每层的形状都类似于一个上宽下窄的倒置漏斗;参数1/2,1/2,1/2,ci1/ci2和tm1/tm2比值均对硐室塌落面的形状有影响;随着参数1/2的比值增大,上层围岩延伸到地表的塌落半径减小,在岩层分界处塌落半径呈现出增大的趋势,从整体上看,硐室的塌落范围增大,下层岩体参数2固定时,随着1的增大,上层围岩和下层围岩的塌落范围都将增大;参数1/2比值对硐室塌落面形状的影响与1/2不同,随着1/2的增大,上层围岩延伸到地表的塌落半径、岩层分界处的塌落半径以及整个塌落体均呈减小的趋势,当下层岩体参数2固定时,随着1的增大,上层围岩和下层围岩的塌落范围均减小;随着参数的增大,上下2层围岩的塌落范围都将减小;参数ci与tm对塌落面形状影响一致,随着ci与tm的增大,上下2层围岩塌落范围都均增大。
4 结论
1) 对于二维浅埋矩形硐室顶部有双层围岩的塌落,无论参数如何变化,硐室塌落面都呈抛物线型,每层的形状都类似于一个上宽下窄的倒置 漏斗。
2) 参数,,,ci和tm均对硐室塌落面的形状有影响;随着参数的增大,上层围岩延伸到地表的塌落半径减小,在岩层分界处塌落半径呈现出增大的趋势;参数对硐室塌落面形状的影响与不同,随着的增大,上层围岩延伸到地表的塌落半径、岩层分界处的塌落半径以及整个塌落体均呈减小的趋势;随着参数的增大,上下2层围岩的塌落范围均减小;参数ci与tm对塌落面形状影响一致,随着ci与tm的增大,上下2层围岩塌落范围均增大。
[1] 张成平, 张顶立, 王梦恕. 浅埋暗挖隧道施工引起的地表塌陷分析及其控制[J]. 岩石力学与工程学报, 2007, 26(2): 3601−3608. ZHANG Chengping, ZHANG Dingli, WANG Mengshu. Analysis of ground subsidence induced by shallow-buried tunnel construction and its control techniques[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 3601−3608.
[2] 张成平, 韩凯航, 张顶立, 等. 城市软弱围岩隧道塌方特征及演化规律试验研究[J]. 岩石力学与工程学报, 2014, 33(12): 2433−2442. ZHANG Chengping, HAN Kaihang, ZHANG Dingli, et al. Test study of collapse characteristics of tunnels in soft ground in urban areas[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(12): 2433−2442.
[3] Hoek E, Carranza-Torres C, Corkum B. Hoek-Brown criterion-2002 edition[C]// Proceedings of NARMS-TAC Conference, Toronto, 2002: 267−273.
[4] Hoek E, Brown E T. Practical estimate the rock mass strength[J]. International Journal of Rock Mechanics and Mining Science, 1997, 34(8): 1165−1186.
[5] ZHAO Lianheng, XIAO Cheng, LIANG Li, et al. Seismic displacement along a log-spiral failure surface with crack using rock Hoek-Brown failure criterion[J]. Soil Dynamics and Earthquake Engineering, 2017, 99(12): 74−85.
[6] DENG Dongping, LI Liang, WANG Jianfeng, et al. Limit equilibrium method for rock slope stability analysis by using the generalized Hoek–Brown criterion[J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 89: 176−184.
[7] Fraldi M, Guarracino F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion[J]. Int J Rock Mech Min Sci, 2009, 46(4): 665–673.
[8] Fraldi M, Guarracino F. Limit analysis of progressive tunnel failure of tunnels in Hoek–Brown rock masses[J]. Int J Rock Mech Min Sci, 2012, 50(5):170–173.
[9] HUANG F, YANG X L. Upper bound limit analysis of collapse shape for circular tunnel subjected to pore pressure based on the Hoek–Brown failure criterion[J]. Tunnelling and Underground Space Technology, 2011, 26(5): 614−618.
[10] YANG X L, HUANG F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion[J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686−691.
[11] QIN C B, YANG X L, PAN Q J, et al. Upper bound analysis of progressive failure mechanism of tunnel roofs in partly weathered stratified Hoek–Brown rock masses[J]. Int J Rock Mech Min Sci, 2015, 74: 157−162.
[12] QIN C B, Chian S C, YANG X L, et al. 2D and 3D limit analysis of progressive collapse mechanism for deep-buried tunnels under the condition of varying water table[J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 80: 255−264.
[13] LIU J, LIU X R, LAI Y, et al. Failure mode of shallow-buried weak tunnel under different thickness- span ratios[J]. Journal of Central South University (Science and Technology), 2016, 47(5): 1744−1751.
[14] HUANG Fu, ZHAO Lianheng, ZHANG Sheng. Effect of surface bolt on the collapse mechanismof a shallow rectangular cavity[J]. Geomechanics and Engineering, 2017, 13(3): 505−515.
[15] QIN C B, Siau Chen Chian. Revisiting crown stability of tunnels deeply buried in non-uniform rocksurrounds[J]. Tunnelling and Underground Space Technology, 2018, 73: 154−161.
Upper bound analysis of two-layer rock collapseoverlying a two dimensional shallow rectangular chamber
ZENG Zhonglin, LI Liang, LIU Shuangyong, ZUO Xuexian
(School of Civil Engineering, Central South University, Changsha 410075, China)
Based on the upper bound theorem of limit analysis and the Hoek-Brown failure criterion, the collapse failure mechanism of two layers shallow tunnels was constructed in this paper, and according to the virtual work principle, a functional was deduced. To obtain the analytic expression of the failure curve, the function of the failure curve and the unknown coefficients were obtained firstly under limit state by means of the variational method and the boundary conditions. Then the research result was consistent with that of single-layer surrounding rock when two-layer surrounding rock degenerates into single-layer surrounding rock, which proved the analytical model in this paper is correct. Lastly, the influence law of each parameter on the collapse failure shape of the two-layer shallow buried tunnel was analyzed, which could provide a theoretical basis for the potential collapse area of surrounding rock in the layered shallow rock.
collapse; two-layer surrounding rock; shallow; Hoek-Brown failure criterion; limit variational analysis
10.19713/j.cnki.43−1423/u.2019.04.020
TU45
A
1672 − 7029(2019)04 − 0984− 08
2018−05−22
国家自然科学基金资助项目(51478477,51878668)
李亮(1962−),男,江苏泰州人,教授,博士,从事道路与铁道工程研究;E−mail:liliang_csu@126.com
(编辑 阳丽霞)
