考虑雷诺数和形状影响的坝岸根石水平水流拖曳力系数修正

兰 雁，沈细中，邹 瑞，杨昌明，蒋思奇，罗立群



考虑雷诺数和形状影响的坝岸根石水平水流拖曳力系数修正

兰 雁1，沈细中1，邹 瑞2，杨昌明3，蒋思奇1，罗立群1

（1. 黄河水利委员会黄河水利科学研究院，郑州 450003；2. 华北水利水电大学土木与交通学院，郑州 450045；3. 南昌大学土木工程与建筑学院，南昌 330000）

对于水利工程坝岸散抛根石冲揭失稳，水流作用下根石的拖曳力是重要的力学分析参数。该文基于黄河坝岸散抛根石的形状参数特征，利用水槽试验量测球体及不同形状块体受水流作用的水平拖曳力，研究雷诺数、物体形状指标与拖曳力相关关系及变化规律，明确影响因素，率定双因素影响下块体的拖曳力系数函数。结果表明，水下球体或近似球状物体的拖曳力系数，基本不受水流及物体形态影响，拖曳力系数趋于0.40～0.56；有棱角块体的水流拖曳力系数，块体雷诺数小于3×104的影响区域，系数函数呈双曲线趋势变化；块体雷诺数大于3×104的影响区域，迎水面宽高比不大于侧立面长高比，拖曳力系数趋于0.80～0.90，迎水面宽高比大于侧立面长高比，拖曳力系数趋于1.00～1.10。进一步通过试验修正了水流作用下不同形态物体的水平拖曳力系数，提出了块体雷诺数、形状参数双因素影响下物体水平拖曳力系数函数，得到了以不同物体来流方向投影响面积为基准的水平拖曳计算公式，经拟合公式的合理性分析与验证，拖曳力系数拟合优度达到0.90以上，平均相对误差为8.7%；修正后拖曳力平均相对误差仅为7.5%，公式计算效果良好，更准确地反映散抛根石的水下受力特征，为分析水下抛石受水流冲击离散形态提供理论依据。

雷诺数；坝；拖曳力系数；根石；形状；球体；块体

0 引 言

散抛根石冲揭走失是坝岸工程失稳的主要原因之一[1-6]，对于水利工程坝岸散抛根石冲揭失稳，水流作用下根石的拖曳力作用是重要力学分析参数[7-11]。水流拖曳力是作用在颗粒上的水流绕流阻力，目前球体或二维圆柱体水平拖曳力有较为成熟的计算公式，其水平拖曳力与作用流速的平方、垂直水流方向的投影响面积成正比，拖曳力系数采用经验值或试验值[12-17]。对于有棱角的块状物体，往往借鉴该公式，来计算块体的拖曳力，如缑元有[18]利用球体水平拖曳力公式分析河道整治工程根石受力状态, 建立了根石走失的物理模型；陈小莉等[19]在球体水平拖曳力、上举力等计算公式的基础上，对块石进行受力分析简化求解了漩涡对块石的吸附作用力，导出了受漩涡作用的水下块石的起动流速。庞启秀等[20-21]通过水槽试验测量了水流作用下不同尺度大颗粒块体受到的水平拖曳力，研究了块体形状对水流拖曳力的影响，并提出了考虑块体形状影响的拖曳力计算公式。

若采用单位面积拖曳力表征不同形状块体的水流作用力，拖曳力系数的大小直接影响着不同形状的物体在相同水流作用下的受力状态。但不同形状的物体拖曳力系数C目前研究得还很不充分，多将块体近似为等体积球体[19]，采用球体拖曳力系数的经验值[18, 22]。对于泥沙或球形物体，基于斯托克斯公式，根据球体沉速与粒径的实测资料，当沙粒雷诺数Re>1 000时，球体下沉属于紊动状态，即拖曳力系数C与沙粒雷诺数Re无关，而接近常数值0.45[12]。李贞儒等[23]通过光滑床面单颗球体试验得到，在Re>2 000、=/2（为球体的/2高度处，为球体直径）时，C值为0.70。对于近似长方体或正方体物体，不同于球体或流线型体的流体分离，流经具有折角的块体的流体分离形式由块体形状决定。Hoerner[24]综合了不同研究者关于长方体的拖曳力系数随长高比（/）变化关系的研究成果表明，在04.0后，随长高比的增加，压强作用力系数缓慢减小，但由于块体长度的增加，摩擦阻力持续增大，在/数值较大（/>4.0）时，由摩擦力和压强作用力组成的合力系数将略微增加，拖曳力系数与块体长高比的关系表现为有一定斜率（斜率为正值）的直线。Evett等[25]直接引用Raymond Binder (1973)的数据资料，给出块体形状雷诺数Re>1 000时的拖曳力系数随宽高比/变化关系，两者呈正比。在/=1.0时，C=1.05；/趋于无穷大时，C=2.05。张磊等[26]分析水中块体稳定性时，拖曳力的计算采用与石块形状及雷诺数有关的函数修正，但未说明函数公式。

与上述研究成果不同，笔者通过模拟散抛根石受力的水槽试验发现，块体拖曳力实测值远大于等体积球体的实测值，特别是流速强度较大时，差异可达1.5～2倍，如将水下块石近似球体计算拖曳力往往小于实测值；且块体拖曳力反映出块体雷诺数、块体形状影响较大，拖曳力系数表现为块体雷诺数、块体形状多因素影响的函数曲线，而不仅仅是单因素影响的范围值。因此，为了真实反映散抛根石受水流冲击的作用力，本文基于黄河坝岸散抛根石的形状参数，利用水槽试验测试球体及不同尺寸块体受水流作用的水平拖曳力，计算相应的拖曳力系数，研究水平拖曳力系数的影响因素，提出不同形状参数物体拖曳力系数取值范围及根石受水流作用的拖曳力公式，为模拟冲揭失稳的水力学边界提供理论依据。

1 材料与方法

1.1 供试材料

1.1.1 黄河坝岸散抛根石形状及迎水面参数调查结果

黄河坝岸散抛根石以近似长方体或正方体的形态堆积，就地取材为石灰岩、砂岩、花岗岩、闪长岩等坚硬岩石，按块石的稳定堆积状态及长度大小顺序，将块石定义长（）、宽（）、高（）3个形状参数，如图1所示，实地量测黄河花园口险工122#坝、马渡险工25#坝及九堡险工118#坝根石尺寸30组及重度15组，统计如表1。由表1可见，根石块体的宽高比分布在1.01～2.55之间，长高比分布在1.29～3.40之间，重度分布在17.70～26.20 kN/m3。

图1 黄河坝岸散抛根石堆积体及块体形态

1.1.2 散抛根石尺寸取值依据

统计散抛根石堆积形态，根石体多以大尺寸为底面，小尺寸为立面形式堆积。根据表1中尺寸定义，根石的宽高比（）及长高比（）均大于或等于1，水下根石受水流冲击迎水面有2种形式：1）以为迎水面，<或=；2）以为迎水面，>。由此可见，根石迎水面受力形态参数可概化为2个组合：组合1为迎水面小于或等于侧面；组合2为迎水面大于，其中组合1是根石受力主要形式，制备样品形态参数可以此为依据，散抛根石尺寸组合统计如表2。

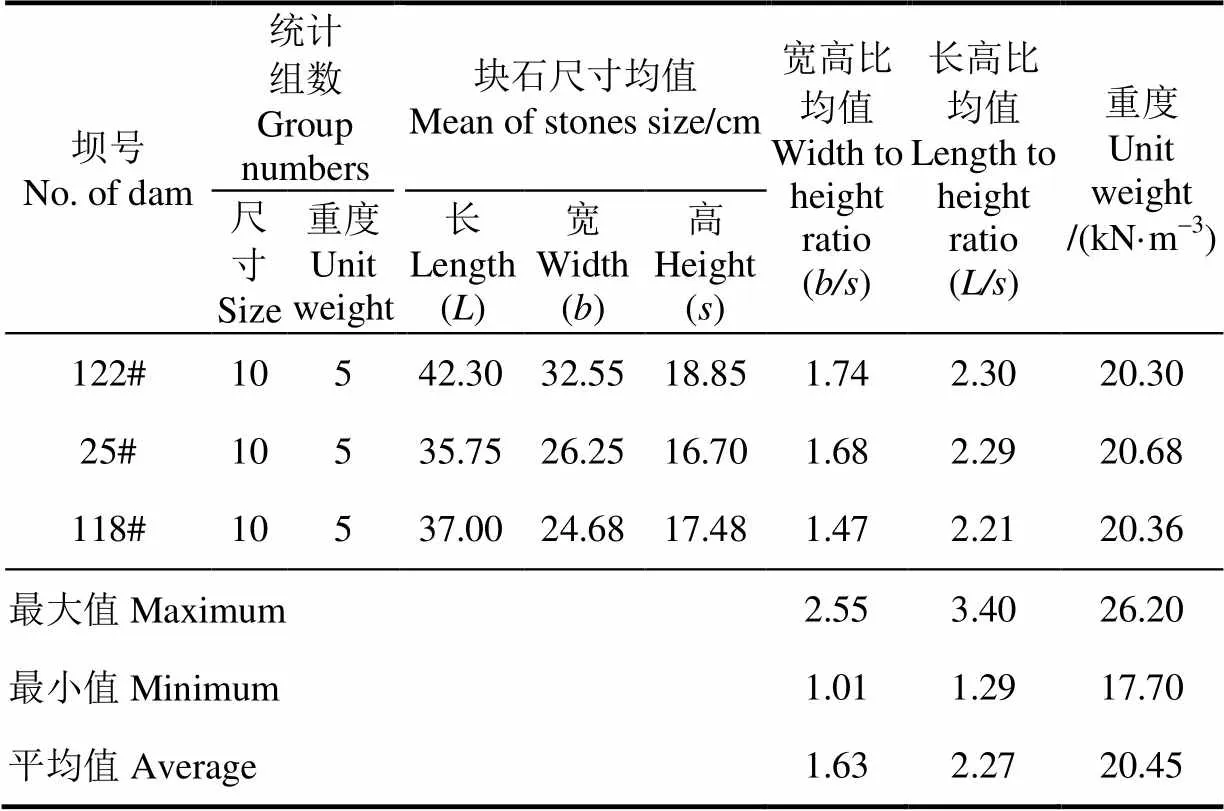
表1 黄河坝岸散抛根石形状参数及重度

表2 散抛根石迎水面及侧面尺寸组合

1.2 试验系统

水流作用下块体拖曳力量测系统由变坡水槽、流速仪、电阻式压力传感器（拖曳力及垂直力）、滑轮支架、四通道信号转换器、wifi无线传输器等设备组成，该系统可实现块体周边流速、块体受水流的水平与垂直压力、各点水压力的实时在线量测与传输。满足水流流速与块体受力的同步不间断量测，获取水流瞬时流速、时均流速、块体水平压力与垂向压力的数据要求。测试系统组成如图2，变坡水槽（长×宽×高50 m×0.6 m× 1.2 m）主要控制水流流量、流速及水位；旋浆式流速仪测量流速，启动流速2.16 cm/s，最小量程0.01 cm/s；电阻式压力传感器测量块体压力，灵敏度（2.0±0.1）mV/V，最小量程1 g；滑轮支架的作用为通过钢丝转换压力方向，直径2.2 cm；wifi信号无线传输，四通道信号转换器为将流速及压力信号转换，流速测点频率为每2 s 1点次，压力测点频次为10点次/s。

图2 块体拖曳力量测试验系统

1.3 试验方案

试验目的是对比球体与块体水平拖曳力系数的差异，宏观上探究块体水平拖曳力系数影响因素，提出块体水平拖曳力计算公式，为此本次试验根据黄河坝岸散抛根石块体形状、重度等参数，制备3组球体、18组块体，测量不同水流强度下球体与块体水平与垂直压力，具体的试验方案如下。

黄河坝岸散抛根石块体尺寸范围为宽高比1.01～2.55，长高比1.29～3.40，重度17.70～26.20 kN/m3，通过块体参数比选测试，边长为2～3 cm的块体尺寸小，试验结果近似球体，边长大于10 cm，水流振荡影响较大。因此，结合护岸根石实际参数比例，考虑试验效果，选用迎水面高度为4 cm的块体为基准，采用预制混凝土材料制备3组球体、18组块体，如图3所示，试验块体宽高比1.00～2.50，长高比1.00～3.75，重度22.40～23.90 kN/m3，具体试块参数如下表3。

注：单位为cm。

表3 试样尺寸参数

试验过程中水槽水位设置为25 cm，含沙量10 kg/m3左右，控制水槽流量，尾门自动调节开启度，试验水流平均流速强度分别控制在25、35、45、55、65、75、85、95、105、115 cm/s的10个阶段瞬时与时均流速，分别量测21组尺寸不同的试块水平与垂直水流作用力。

1.4 测量及计算方法

1.4.1 流速及拖曳力测量方法

1）利用安装有定滑轮的测力支架，通过钢丝线将试验块体悬浮在变坡水槽一定水深位置（距水槽底部10 cm），以试块参数的宽、高方向为迎水面。2）将流速仪放置于试块中心同一深度，通过微转子式流速传感器测量水流瞬时流速，计算不同流量阶段的时均流速。3）水平拖曳力通过定滑轮改变至垂直方向压力传感器实时采集。4）流速、压力传感器信号通过电缆传输到四通道信号转换器，继而将数据通过wifi无线传输器传至电脑。量测方法如图4。

图4 拖曳力量测系统

1.4.2 拖曳力及雷诺数计算方法

1）水平拖曳力公式

对于淹没于水中的球体或二维圆柱体受到的水平拖曳力，Evett等[25]提出的水平拖曳力公式为

式中F为水平拖曳力，N；C为拖曳力系数；为浑水重度，N/m3；为球体或圆柱体中心作用的水流流速，m/s；为球体或圆柱体在垂直于来流方向的投影面积，m2；为重力加速度，m/s2。

对于球体或近于球体的泥沙、卵石等物体，垂直于来流方向的投影面积是定值，而对于近似于长方体或正方体块石等物体，垂直于来流方向的投影面积与迎水面的块体长度与高度密切相关，如分析不同形状物体的水下受力情况，在式（1）的基础上，将水平拖曳力变换为单位面积的水平拖曳力公式[18]如下：

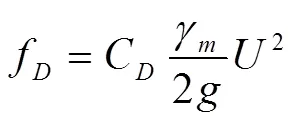
式中f为单位面积的水平拖曳力，N/m2；为块体中心作用的水流时均流速，m/s。

2）块体雷诺数计算公式

雷诺数是描述流体动规律的无量纲数群，表征流动中流体惯性力和黏性力之比[27-28]。流体流动、沉降、传热、吸收、干燥等，雷诺数的表达式和临界值各有不同[29]，块体形状雷诺数（Re）常用于表征流体浇流经过块体情况的无量纲，主要与流场的特征速度、块体的主要尺寸相关[20,30]，计算公式如下：

式中为流体密度，kg/m3；为流体动力黏滞系数，Pa·s。

1.5 曲线拟合优度计算公式

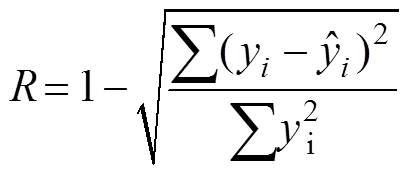
式中把残差平方和与相对误差有机地结合在一起，几何意义清晰，越接近于1，表示曲线的拟合优度越好。

2 结果与分析

2.1 球体与块体的拖曳力系数分析

以迎水面投影面积及形状参数相似为原则，对比5 cm球体与4 cm×4 cm×4 cm块体、6 cm球体与5 cm×5 cm×5 cm的块体雷诺数与拖曳力关系曲线，以及7.5 cm球体的球体雷诺数与拖曳力关系曲线如图5。

由图5可知：1）球体水平拖曳力系数在0.40～0.56之间，随形状及球体雷诺数变化影响不大；2）块体水平拖曳力系数在雷诺数0.76×104～2.62×104时，水平拖曳力系数随着块体雷诺数增加而增加，雷诺数>2.62×104后，水平拖曳力系数趋于恒定，平均值为0.82；3）块体拖曳力系数随块体雷诺数增长有上升到稳定的过程，不同尺寸的块体趋势有差异，由此可见雷诺数及形状参数的变化对块体水平拖曳力系数有一定的影响。

2.2 块体雷诺数对块体的拖曳力系数影响分析

试验分析可见块体雷诺数与水平拖曳力系数密切相关，迎水面试验块体的高度不变，改变通过块体中心的时均流速，绘制块体雷诺数与水平拖曳力系数变化的关系曲线，分析不同宽高比、长高比块体的水平拖曳力与块体雷诺数的变化趋势，如图6。

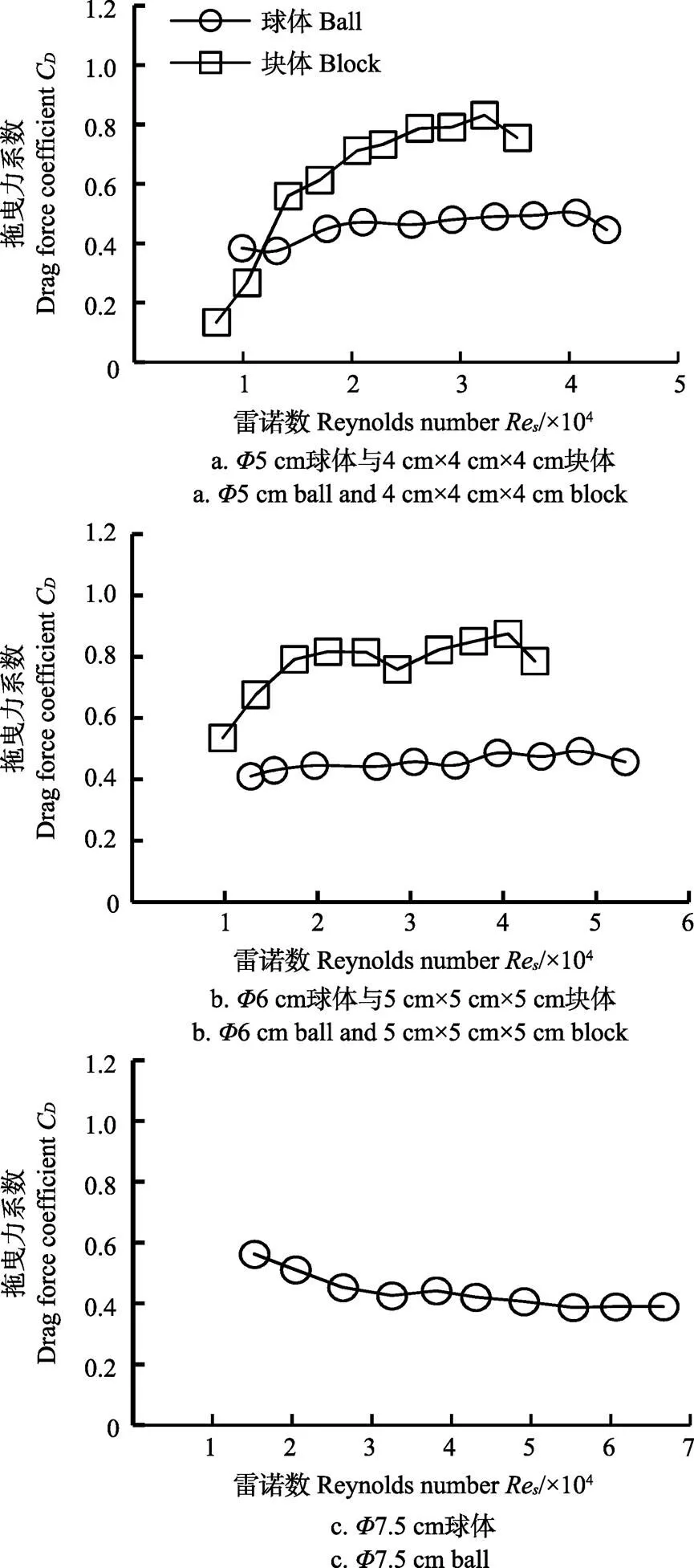
图5 球体与块体雷诺数与水平拖曳力系数关系曲线

由图6：1）Re<2×104时，拖曳力系数随块体雷诺数增大而增大，斜率增长相对较大；2）Re界于2×104～3×104之间，拖曳力系数趋于平稳，斜率增长相对较小；3）≤，Re>3×104时，拖曳力系数趋于0.80～0.90；>，Re>3×104时，拖曳力系数趋于1.00～1.10；4）当块体雷诺数≤3×104时，块体拖曳力系数随块体雷诺数似呈双曲线趋势变化，同时不同形状参数的变化曲率不同；当块体雷诺数大于3×104时，块体拖曳力系数趋于恒定；

2.3 块体形状参数对块体的拖曳力系数影响分析

与球体或近似球体的物体不同，块体具有投影各向异性、边界棱角不规则等特性，宽高比对块体迎水面压强，长高比对侧向摩擦力的影响较大，直接影响水流对块体作用力的变化，为探究块体形状参数对拖曳力系数的影响，根据试验成果，规定相同条件下，分析不同宽高比、长高比与拖曳力系数的关系。

图6 块体雷诺数与水平拖曳力系数关系曲线

2.3.1 宽高比（/）对拖曳力系数影响

为分析迎水面宽高比对拖曳力系数的影响，保持块体长宽比（/）恒定，绘制块体不同迎水面宽高比与拖曳力系数的关系曲线，如图7。由图7可知：1）/≤2.0，Re≤2×104时，宽高比对拖曳力系数影响较大，拖曳力系数随宽高比增大总体趋于增大；2）/>2.0，Re≤2×104时，拖曳力系数趋于恒定；3）Re>2×104时，宽高比对拖曳力系数影响不大，拖曳力系数趋于恒定；4）块体≤，块体雷诺数Re≤2×104，/≤2时，块体拖曳力系数随块体雷诺数呈正向线性变化，当/>2时，块体拖曳力系数基本趋于恒定；当块体雷诺数Re>2×104时，块体拖曳力系数趋于恒定。同样，根据试验成果，块体>、/>2时，块体拖曳力系数趋于恒定。

图7 块体宽高比与水平拖曳力系数关系曲线（b/s≤L/s）

2.3.2 长高比(/)对拖曳力系数影响

长高比对拖曳力系数的影响，保持块体宽高比（/)、块体雷诺数恒定，绘制块体不同长高比与拖曳力系数的关系曲线，如图8。

由图8：1）Re≤2×104，/≤1.5时，长高比对拖曳力系数影响较大，拖曳力系数随宽高比增大而增大，似呈线性增长；2）Re≤2×104，/>1.5时，拖曳力系数趋于恒定；3）Re>2×104时，长高比对拖曳力系数影响不大，拖曳力系数趋于恒定。4）试验块体/≤，/≤1.5时，拖曳力系数呈正向线性变化；/>1.5时，图形趋于定值。同样，根据试验成果，块体/>，1≤/<2时，块体拖曳力系数趋于呈反向线性变化。

图8 块体长高比与水平拖曳力系数关系曲线（b/s≤L/s）

3 块体拖曳力系数修正公式及验证

根据块体拖曳力随块体雷诺数、形状参数变化趋势及相关关系，可将影响因子融入块体拖曳力系数，设定应用条件提出双因素影响下块体拖曳力系数计算公式。

3.1 修正前拖曳力计算公式

修正前对于块体拖曳力计算公式中拖曳力系数的取值，学者们在工程实践中多将块体近似为等体积球体，采用球体拖曳力系数的经验值，即泥沙或球形物体沙粒雷诺数Re>1 000时，拖曳力系数C接近常数值0.45[12]。

如缑元有[18]通过对河道整治工程根石受力状态的分析，建立了根石走失的物理模型，导出了天然河道根石走失的力学计算公式，其中计算根石临界启动长度时，假设雷诺数≥1 000时，C取值为0.43。江胜华等[22]在总结已有冲刷机理的基础上，分析了包括墩前河床底部流速和墩侧河床底部流速的桥墩局部流速，并给出了桥墩冲刷防护石块起动的简化公式计算公式，其中在计算桥墩冲刷防护石受水流拖曳力计算式中，C取值为0.40。因此，工程实践中，拖曳力系数常采用定值0.45，修正前拖曳力计算公式为

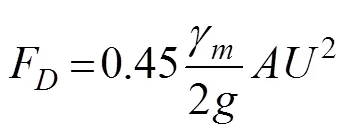
式中为块体的等体积球体当量投影面积，m2。

笔者通过试验发现，块体拖曳力实测值远大于等体积球体的实测值，特别是流速强度较大时，差异可达1.5～2倍，如将水下块石近似球体计算拖曳力往往小于实测值；且块体拖曳力反映出块体雷诺数、块体形状影响较大，拖曳力系数表现为块体雷诺数、块体形状多因素影响的函数曲线，而不仅仅是单因素影响的范围值。

3.2 双因素影响下拖曳力修正计算公式

3.2.1 拖曳力系数修正公式

考虑块体雷诺数及几何尺寸的2种因素交互影响，根据试验成果分析，在一定的应用条件下，块体拖曳力系数随块体雷诺数（Re）呈双曲线函数变化，随形状参数（）呈线性函数变化。利用文献[33]中双因素影响计算公式拟合方法，考虑到二者的交互影响，将2个影响因子按乘法效应进行组合，得到7种组合应用条件下的块石水平拖曳力系数公式。基于试验量测数据，利用最小二乘法拟合不同应用条件下拖曳力系数公式，修正得到形状参数（）、块体雷诺数（Re）块石拖曳力系数拟合公式如下：

式中为块体长，m；为块体迎水面宽，m；为块体迎水面高，m；1(,,)和1(,,)为与相关的函数；为常量；为10-4Re。

其中：

1）当迎水面≤时，

a. 若Re≤2×104，≤1.5，≤1.5，则

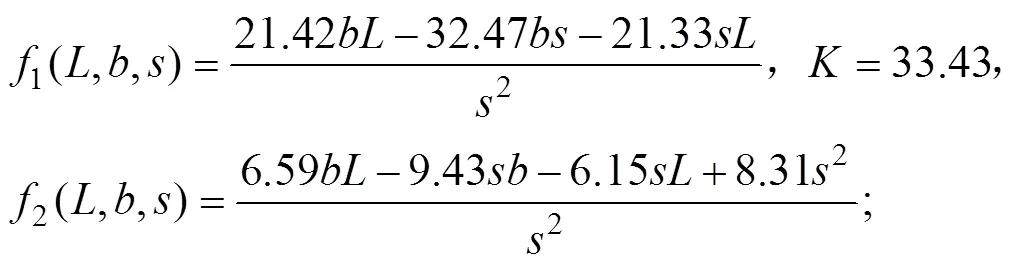
b. 若Re≤2×104，/≤1.5，1.5＜/≤4.0，则

c. 若2×104<Re≤3×104，≤1.5，/≤1.5，则

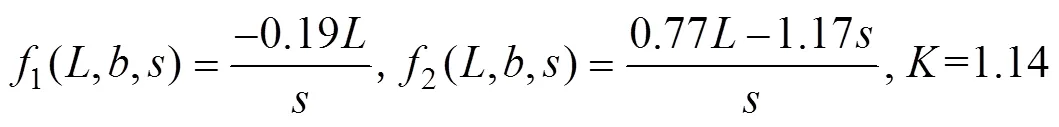
2）当迎水面/>/，Re<2×104，/≥2.0，/<2.0时，则

式中为块体雷诺数的10-4，其中：

迎水面/≤/时

a. 若Re≤2×104，1.5

b. 若2×104<Re≤3×104，1.5

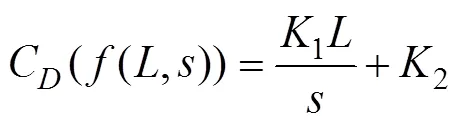
式中为块体长，m；为块体迎水面高，m。其中：迎水面/≤/，Re≥3×104，/≤1.5，1=0.11，2=0.71。

当迎水面尺寸宽高比/≤长高比/，Re≥3×104，1.5≤/<4.0，C的取值为0.80～0.90；当迎水面尺寸宽高比/>长高比，Re≥3×104，C的取值为1.00～1.10。

3.2.2 块体拖曳力修正公式

基于黄河坝岸散抛根石形状参数统计，利用基础水槽量测水下块体受水流作用力变化过程，结果分析表明块体雷诺数、形状参数对拖曳力系数影响较大。将式（2）中拖曳力系数修正为与块体雷诺数与形状参数相关的函数，则块体单位面积水流拖曳力修正的计算公式如下：

式中f为单位面积的水流拖曳力，N/m2；C为拖曳力系数函数，为不同应用条件相关取值，如式（6）～式（8）；为浑水重度，N/m3；为块体中心作用的水流时均流速，m/s。

淹没于水流中水流作用力下块体受到的水平拖曳力计算公式如下：

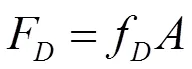
式中F为水流拖曳力，N；为块体在垂直于来流方向的投影面积，m2。

3.3 修正公式验证试验及结果

3.3.1 拖曳力系数修正的合理性分析

为验证块体形状参数与雷诺数双因素影响下拖曳力系数拟合公式的合理性，分析不同雷诺数正方体4 cm× 4 cm×4 cm拖曳力系数的实测值与公式拟合值的相关性，拖曳力系数实测值与计算拟合值趋势如图9a，采用拟合优度及平均相对误差（mean of relative error，MRE）判断验证结果[34]，拟合优度（）可达0.93，MRE为3.9%。Re≤2×104、/≤1.5、/≤1.5条件下拖曳力系数实测值与公式拟合值趋势如图9b，拟合优度可达0.90，平均相对误差为8.7%。

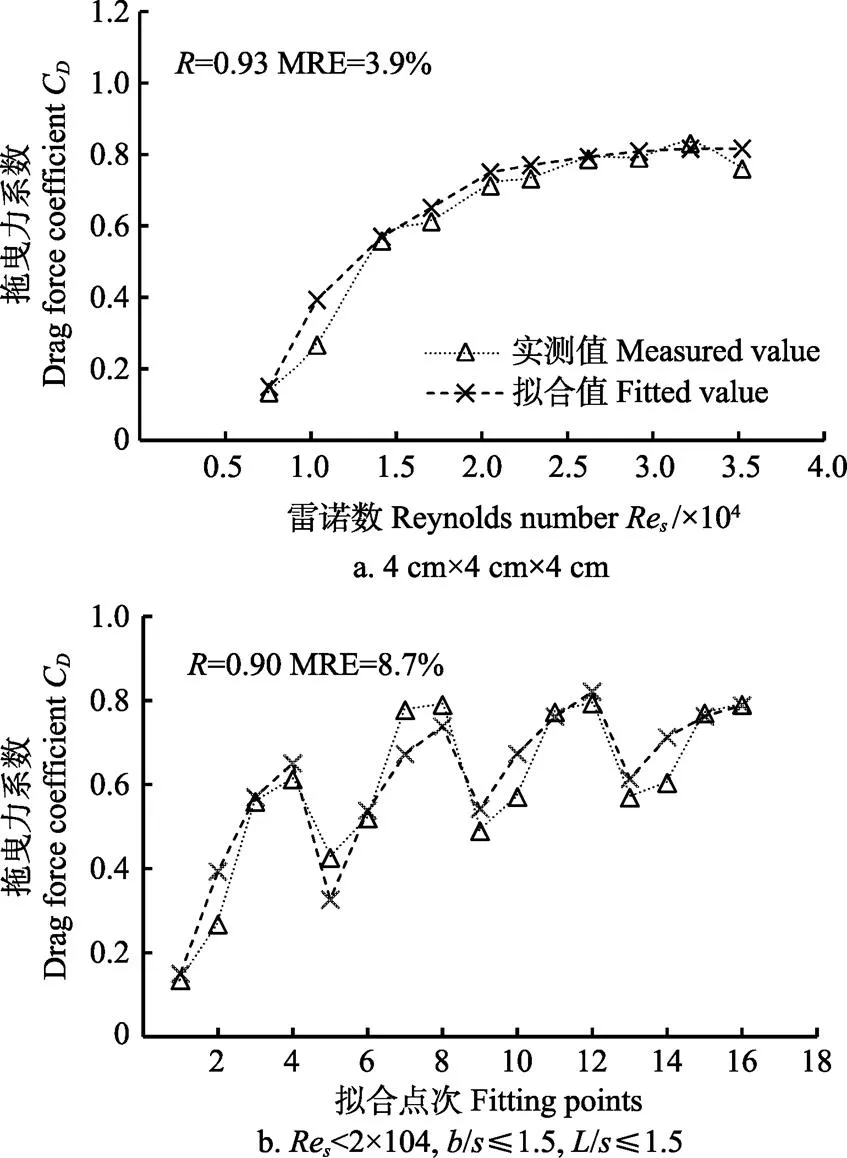
图9 双因素影响下拖曳力系数拟合曲线

3.3.2 拖曳力修正公式的验证

1）验证试验设计

为了验证公式的有效性和准确性，制作块体为5 cm× 5 cm×5 cm的标准铝块，重度28.8 kN/m3，试验过程中水槽水位设置为25 cm，含沙量10 kg/m3左右，控制水槽流量，尾门自动调节开启度，试验水流平均流速强度分别控制在35、45、55、66、74、86、96、105、113 cm/s的9个阶段瞬时与时均流速，测试水下块体的拖曳力变化，测力系统如图10。

图10 拖曳力系数修正公式验证试验系统

2）拖曳力修正公式验证结果分析

根据验证试验获取的瞬时流速及瞬时拖曳力数据，统计各水流强度控制下的流速、拖曳力及拖曳力系数的实测值如表4。采用拖曳力系数0.45的取值，利用修正前拖曳力计算公式，如式（5），计算值与实测值的MRE达到31.9%，拖曳力的计算值远小于实测值，由此可见，修正前拖曳力计算公式与验证试验结果吻合较差。而根据标准块体形状及块体雷诺数，按不同应用条件的修正公式得到拖曳力系数的拟合值，修正后的拖曳力计算值与实测值的平均相对误差为7.5%，表明试验验证结果与实测值吻合较好，修正后公式与试验值更相符。

通过多组块石水平拖曳力试验、公式优化拟合及标准试块验证试验，可以认为拖曳力系数拟合公式可以用于块体迎水面高度不小于4 cm、块体雷诺数大于0.75×104的水下块石的水平拖曳力计算。试验成果弥补了工程中水下块体拖曳力系数取值理论依据不足的问题，可以应用到坝岸散抛根石的护岸工程的规划与设计中。

表4 拖曳力系数修正公式验证试验成果

4 讨 论

对于块体拖曳力系数取值，目前研究成果或近似采用球体拖曳力系数，或仅考虑了单因素（如形状参数、雷诺数）对拖曳力系数的影响，本研究成果模拟黄河坝岸散抛根石形态参数，开展多组系列基础水槽试验块石水下受力冲刷试验，在前人研究的基础上考虑块体形状及雷诺数双因素的影响，取得了一定条件下块体拖曳力系数拟合公式及拖曳力修正公式，并通过标准块体的公式验证，修正后的拖曳力计算值与实测值的平均相对误差为7.5%，公式计算效果良好。证明拖曳力系数拟合公式适用于块体不小于4 cm、Re大于0.75×104的水下块石的水平拖曳力计算。试验成果弥补了护岸工程稳定性计算过程中，水下块体拖曳力系数取值理论依据不足的问题。

通过块体受力水槽试验，笔者在获取块体拖曳力同时，也得到一系列上举力测试数据，分析表明，块体拖曳力变化规律随流场及块体形状影响变化明显，而上举力值偏小，且与流场及块体形状无明显的相关关系，个别块体在上举力量测过程中，受块体在水中振荡姿态的干扰影响相对较大。上举力总体规律为：球体的上举力是拖曳力的1/4～1/5，上举力系数趋于0.1；块体的上举力是拖曳力的1/8～1/10，上举力系数也趋于0.1。上举力规律与文献[23]中提出的球体上举力0.18，文献[20]中块体上举力0.12左右取值类似，证明测试数据及规律的可靠性。

为探究护岸工程堆石形态对抛石走失的影响，笔者也尝试开展了多块体不同堆积形态的拖曳力试验，试验发现，随着块体不同组合形式的改变，目标块体迎水水流流速也随之变化，流场分布变异性较大，但组合形式目标块体与单块体拖曳力变化规律一致，由此可见，单块体基础水槽试验可规律性地反映了块石个体拖曳力随块体形状及雷诺数变化情况，试验成果适用于坝岸散抛根石水流冲刷作用边界力的设定。鉴于此，考虑雷诺数和形状影响的块石水平拖曳力成果，应与坝岸的流场分布相结合，适用于预测暴露在坝岸迎水侧及坝头的护岸块石受到的水流冲揭力，实践证明，受水流瞬时或周期性冲击作用，暴露在坝岸迎水侧及坝头的护岸块石极易冲揭启动。

5 结 论

黄河坝岸散抛根石水流作用力水槽模拟试验研究表明，不同块体雷诺数、形状参数直接影响拖曳力系数变化，通过多种组合试验的分析验证，得出相关结论如下：

1）水下球体或近似球体的物体的水流水平拖曳力系数，基本不受水流及物体尺寸影响，拖曳力系数在0.40～0.56。

2）有棱角块体（≥4 cm、Re>0.75×104）的水流水平拖曳力系数，以单位面积水流拖曳力分析其规律，水流与物体形态参数（即块体雷诺数、迎水面压强、顺水面块体摩擦力）协同影响水流拖曳力系数的变化，集中反映在块体雷诺数小于3×104的影响区域，系数函数趋于双曲线形态变化；块体雷诺数大于3×104的影响区域，迎水面≤侧立面时，拖曳力系数趋于恒定值0.80～0.90，迎水面>侧立面时，拖曳力系数趋于恒定值1.00～1.10。

3）通过试验率定并验证了水流作用下不同形态物体的水平拖曳力系数，提出了块体雷诺数、形状参数双因素影响下物体水平拖曳力系数函数公式，得到了以不同物体来流方向投影面积为基准的水平拖曳力计算公式，更准确地反映散抛根石的水下受力特征。

4）通过拖曳力系数修正公式的合理性分析，拖曳力系数修正公式拟合优度达到0.90以上，平均相对误差为8.7%；标准块体的公式验证修正后拖曳力平均相对误差仅为7.5%，公式计算效果良好。证明拖曳力系数拟合公式可以用于块体不小于4 cm、Re大于0.75×104的水下块石的水平拖曳力计算。试验成果弥补了护岸工程稳定性计算过程中，水下块体拖曳力系数取值理论依据不足的问题，可以应用到水利工程护岸工程规划与设计中。

[1] 郭秀华，杜学军，魏凤. 黄河下游险工坝岸根石走失规律及其防护措施探讨[C]. 山东水利科技论坛，2007：269－272.

[2] 郭全明，张亚丽，薛选世，等. 黄河小北干流河道工程出险原因及防护对策[J]. 人民黄河，2012，34(11)：7－9. Guo Quanming, Zhang Yali, Xue Xuanshi, et al. Discussion on causes and protective countermeasures of river engineering works in danger of xiaobeiganliu of the Yellow River[J]. Yellow River, 2012, 34(11): 7－9. (in Chinese with English abstract)

[3] 张建怀，崔云雪，连志军. 黄河坝岸根石走失原因及防护措施[J]. 山东水利，2000(6)：14－15.

[4] 包家全，董强，王辉. 黄河河道整治工程根石走失原因及防护措施[J]. 人民黄河，2003，25(11)：17－18. Bao Jiaquan, Dong Qiang, Wang Hui. Analysis on causes of foundation rock loss of river training works of the yellow river and measures for prevention[J]. Yellow River, 2003, 25(11): 17－18. (in Chinese with English abstract)

[5] 苗长运，郭西方，齐洪海. 黄河河道整治工程根石走失及加固研究[J]. 人民黄河，2004，26(2)：25－26. Miao Changyun, Guo Xifang, Qi Honghai. Study on root rock loss and reinforcement of river training works of the yellow river[J]. Yellow River, 2004, 26(2): 25－26. (in Chinese with English abstract)

[6] 郑付生，陈太平，郭文. 河道坝岸根石走失原因及加固措施[J]. 黄河水利职业技术学院学报，2002，14(1)：14－15. Zheng Fusheng, Chen Taiping, Guo Wen. Reasons and protective measures of root rock loss in the Yellow River dam bank[J]. Journal of Yellow River Conservancy Technical Institute, 2002, 14(1): 14－15. (in Chinese with English abstract)

[7] 光治河，徐荣安，刘英杰，等. 黄河河道整治工程坝岸根石走失原因和防护措施[J]. 科技信息，2010(15)：366－367.

[8] 蔡喆伟，夏云峰，徐华，等. 深水航道整治中新型结构淹没丁坝水流力特性研究[J]. 水利水运工程学报，2018(3)：16－23. Cai Zhewei, Xia Yunfeng, Xu Hua, et al．Flow force characteristics of new-type structure submerged spur dike during deep waterway regulation[J]. Hydro-Science and Engineering, 2018(3): 16－23. (in Chinese with English abstract).

[9] 刘大有，王光谦，李洪州. 泥沙运动的受力分析：关于碰撞力的讨论[J]. 泥沙研究，1993，12(2)：41－47.Liu Dayou, Wang Guangqian, Li Hongzhou. Force analyses of sediment transport: A discussion on the “collision force” [J]. Journal of Sediment Research, 1993, 12(2): 41－47. (in Chinese with English abstract)

[10] 丁文斌，史东梅，何文健，等. 放水冲刷条件下工程堆积体边坡径流侵蚀水动力学特性[J]. 农业工程学报，2016，32(18)：153－161.

Ding Wenbin, Shi Dongmei, He Wenjian, et al. Hydrodynamic characteristics of engineering accumulation erosionunder side slope runoff erosion process in field scouring experiment [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(18): 153－161.(in Chinese with English abstract)

[11] 张玮，瞿凌锋，徐金环. 山区河流散抛石坝水毁原因分析[J].水运工程，2003，351(4)：10－12. Zhang Wei, Qu Lingfeng, Xu Jinhuan. Stability analysis of enrockment dams in mountain streams[J]. Port & Waterway Engineering, 2003, 351(4): 10－12. (in Chinese with English abstract)

[12] 谢鉴衡. 河流泥沙工程学[M]. 北京：水利电力出版社，1981：20.

[13] 钱宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，2003：114－122.

[14] Patnaik P C, Pande P K, Vittal N. Drag coefficient of a stationary sphere in gradient flow[J]. Journal of Hydraulic Research, 1992, 30(3): 389－402.

[15] 窦国仁. 再论泥沙起动流速[J]. 泥沙研究，1999，12(6)：1－9.Dou Guoren. Incipient motion of coarse and fine sediment[J]. Journal of Sediment Research, 1999, 12(6): 1－9. (in Chinese with English abstract)

[16] 吴野，王胤，杨庆. 考虑钙质砂细观颗粒形状影响的液体拖曳力系数试验研究[J]. 岩土力学，2018，39(9)：1001－1011. Wu Ye, Wang Yin, Yang Qing. Experimental study on the drag force coefficient of calcareous sand in liquid considering the effect of particle shape[J]. Rock and Soil Mechanics, 2018, 39(9): 1001－1011. (in Chinese with English abstract)

[17] 周双，张根广，邢茹，等. 床面均匀沙拖曳力及上举力系数的确定[J]. 泥沙研究，2016(2)：1－6. Zhou Shuang, Zhang Genguang, Xing Ru, et al. Determination of drag and lift coefficients of uniform sediment on the bed surface[J]. Journal of Sediment Research, 2016(2): 1－6. (in Chinese with English abstract)

[18] 缑元有. 河道整治工程根石走失的力学分析研究[J]. 人民黄河，2000(4)：4－5. Gou Yuanyou. Mechanics analysis and study of root rock loss in river channel harness projects[J]. Yellow River, 2000 (4): 4－5. (in Chinese with English abstract)

[19] 陈小莉，马吉明. 受漩涡作用的水下块石的起动流速[J]. 清华大学学报：自然科学版，2005，45(3)：315－318. Chen Xiaoli, Ma Jiming. Critical velocity for initiation motion of rocks under water due to vortex motion[J]. Journal of Tsinghua University: Science and Technology, 2005, 45(3): 315－318. (in Chinese with English abstract)

[20] 庞启秀. 水流作用下块体受力试验研究[D]. 南京：河海大学，2005. Pang Qixiu. Experimental Study of the Hydrodynamic Forces on the Square-section Cylinder[D]. Nanjing: Hohai University, 2005. (in Chinese with English abstract)

[21] 庞启秀，徐金环，辛海霞. 块体形状对水流推移力的影响[J].水道港口，2006，27(1)：5－8，22. Pang Qixiu, Xu Jinhuan, Xin Haixia. Effect of square -section cylinder shape on the drag force[J]. Journal of Waterway and Harbour, 2006, 27(1): 5－8, 22. (in Chinese with English abstract)

[22] 江胜华，周智，欧进萍. 桥墩局部冲刷防护的石块起动[J]. 泥沙研究，2013(4)：63－67. Jiang Shenghua, Zhou Zhi, Ou Jinping. Incipient motion of rocks for bridge local scour protection[J]. Journal of Sediment Research, 2013(4): 63－67. (in Chinese with English abstract)

[23] 李贞儒，陈媛儿，赵云. 作用于床面球体的推力及举力试验研究[C]//第二次河流泥沙国际学术讨论会论文集. 北京：水利电力出版社，1983：330－343． Li Zhenru, Chen Yuaner, Zhao Yun. Laboratory investigation on drag and lift forces acting on bed spheres[C]. Proceedings of the Second International Symposium on River Sedimentation. Beijing: Water Resources and Electric Power Press, 1983: 330－343. (in Chinese with English abstract)

[24] Hoerner S F. Fluid-dynamic Drag[M]. Bricktown New Jersey: Hoerner S F, 1958: 12－13.

[25] Evett J B, Liu C. Fundamentals of Fluid Mechanics[M]. New York: MeGraw-Hill, 1987: 381－390.

[26] 张磊，徐啸. 后石电厂排水口冲刷及其防护块体稳定试验研究[J]. 水利水运工程学报，2011(2)：14－19. Zhang Lei, Xu Xiao. Scour of the outfall and protection stones stability of Houshi Power Plant[J]. Hydro-Science and Engineering, 2011(2): 14－19. (in Chinese with English abstract)

[27] 陈玉璞. 流体动力学[M]. 南京：河海大学出版社，1990：201－207.

[28] 杨坪坪，王云琦，张会兰，等. 降雨强度和单宽流量与地表粗糙度交互作用下坡面流阻力特征[J]. 农业工程学报，2018，34(6)：145－151. Yang Pingping, Wang Yunqi, Zhang Huilan, et al. Characteristics of overland flow resistance under interaction of rainfall intensity and unit discharge and surface roughness [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(6): 145－151.(in Chinese with English abstract)

[29] 张小璇，张大观. 雷诺数的应用浅析[J]. 广东化工，2014，41(10)：204－206. Zhang Xiaoxuan, Zhang Daguan. The application of the reynolds number[J]. Guangdong Chemical Industry, 2014, 41(10): 204－206. (in Chinese with English abstract)

[30] 陈启刚，齐梅兰，李金钊. 明渠柱体上游马蹄涡的运动学特征研究[J]. 水利学报，2016，47(2)：158－164.Chen Qigang, Qi Meilan, Li Jinzhao. Kinematic characteristics of horseshoe vortex upstream of circular cylinders in open channel flow[J]. Journal of Hydraulic Engineering, 2016, 47(2): 158－164. (in Chinese with English abstract)

[31] 舒继森，郭兵兵，张俊阳. 基于拟合优度指标评价的岩土参数概率分布研究[J]. 采矿与安全工程学报，2008，25(2)：197－201. Shu Jisen, Guo Bingbing, Zhang Junyang. Research on probability distribution of parameters of rock and soil based on fitting optimization index[J]. Journal of Mining and Safety Engineering, 2008, 25(2): 197－201. (in Chinese with English abstract)

[32] 张世强. 曲线回归的拟合优度指标的探讨[J]. 中国卫生统计，2002，19(1)：9－11. Zhang Shiqiang. Approach on the fitting optimization index of curve regression[J]. Chinese Journal of Health Statistics, 2002, 19(1): 9－11. (in Chinese with English abstract)

[33] 沈细中，管新建，兰雁. 非饱和黏土有效应力强度指标计算[J]. 岩土力学，2007，28(S1)：207－210.Shen Xizhong, Guan Xinjian, Lan Yan. Calculation of effective strength indexes of unsaturated low liquid limit clay[J]. Rock and Soil Mechanics, 2007, 28(S1): 207－210. (in Chinese with English abstract)

[34] 穆艾塔尔·赛地，丁建丽，崔春亮. 基于地形因子改进融雪径流的模拟及验证[J].农业工程学报，2017，33(19)：179－186.Muattar·Saydi, Ding Jianli, Cui Chunliang. Simulation and validation of enhanced snowmelt runoff model with topographic factor [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 179－186. (in Chinese with English abstract)

Modification of horizontal drag force coefficient of bam bank root stone considering influence of Reynolds number and shape

Lan Yan1, Shen Xizhong1, Zou Rui2, Yang Changming3, Jiang Siqi1, Luo Liqun1

(1450003,; 2.,450045,; 3.,330000,)

Scattered root stone loss under the action of water flowis one of main reasons causing bank instability. Drag force is an important parameter for understanding the related mechanisms. In this paper, we investigated the effects of shape and Reynolds number on the drag force coefficient of root stone under the action of water flow. Scattered root stones on Yellow River bank had the width-height ratio of 1.01-2.55, the length-height ratio of 1.29-3.40, and unit weight of 17.70-26.20 kN/m3. Based on these investigated results, samples of different shapes (block and ball) and sizes were prepared. A set of force measurement system was developed for determining velocity and pressure signals simultaneously, which could measure horizontal drag force under the action of water flow on balls and different sizes of blocks by controlling water flow of sloping flume. Based on the analysis on the relationship between Reynolds number, shape and drag force, drag coefficient function of block was calibrated. Results showed that the drag force coefficients of underwater balls or balls were not influenced by the flow and shape. Their drag force coefficients were 0.40-0.56. However, the drag force coefficient of blocks was affected by the water flow and object shape. When the Reynolds number of block was less than 3×104, the drag force coefficient changed in hyperbolic shape.When the Reynolds number of block was greater than 3×104, if the width-height ratio of upstream face was less than or equaled to the length-height ratio of upstream of side elevation, the drag coefficients tended to be constant values of 0.80-0.90, or if the width-height ratio of upstream face was more than the length-height ratio of upstream of side elevation, the drag coefficients tended to be constant values of 1.00-1.10. Considering the interaction effects of the Reynolds number and block shape, the horizontal drag force coefficient formula of block stone could be obtained under 7 combination conditions. Based on the measured data, the drag coefficients under different application conditions were fitted by least square method. The formulas of drag force coefficients of block stone were presented under the influence of Reynolds number and shape parameters. And then the horizontal drag force calculation formula was suggested with the projected area of different objects in the flow direction. It could more accurately reflect the force characteristics of the underwater root stone. The goodness of fit of drag force coefficient reached above 0.90, and the mean of relative error was 8.7%. After correction the mean of relative error of drag force was only 7.5%. Compared to the regular method considering the drag coefficient as a constant of 0.45 (the mean relative error of drag force), the corrected method had a higher accuracy, indicating that the modification in this study is reasonable and the formula established is useful for block root stones. The research results make up for inadequacy of theoretical basis for drag force analysis of underwater root stones in the process of revetment engineering stability calculation. These results can be applied to planning and designing revetment projects in water conservancy projects.

Reynolds number; dams; drag force coefficient; root stone; shape; ball; block

2018-07-03

2019-01-01

国家自然科学基金项目( 51509104、51609095)；重大自然灾害监测预警与防范重点专项（2017YFC1501202）

兰雁，教授级高工，主要从事水利工程安全评价理论与应用研究。Email：18091025@qq.com

10.11975/j.issn.1002-6819.2019.05.021

U656.35

A

1002-6819(2019)-05-0173-10

兰 雁，沈细中，邹 瑞，杨昌明，蒋思奇，罗立群.考虑雷诺数和形状影响的坝岸根石水平水流拖曳力系数修正[J]. 农业工程学报，2019，35(5)：173－182.doi：10.11975/j.issn.1002-6819.2019.05.021 http://www.tcsae.org

Lan Yan, Shen Xizhong, Zou Rui, Yang Changming, Jiang Siqi, Luo Liqun. Modification of horizontal drag force coefficient of bam bank root stone considering influence of Reynolds number and shape [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(5): 173－182. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.05.021 http://www.tcsae.org