基于可靠性的围岩失稳规模预测
2018-10-10晏鄂川崔学杰
陈 武,晏鄂川,崔学杰,陈 前
(中国地质大学(武汉)工程学院,湖北 武汉 430074)
地下工程岩体由于被各类结构面切割而形成形状各异的镶嵌块体,在地下工程开挖后,部分块体失稳,为了研究这些块体的塌落和运动规律,Goodman等[1]和石根华[2]分别提出了块体理论。近年来国内外许多学者对块体理论进行了多方面的研究[3-6],对地下工程岩体的稳定性研究起到了一定的推动作用。然而,块体理论中结构面完全贯穿岩体的假定与实际中结构面的有界性不相符,且未考虑结构面间距对块体体积的制约作用。赵文[7]指出构成块体棱锥结构面的长度必须大于所包含棱的长度,由此根据概率论理论给出了迹长负指数分布的关键块体的真正滑落概率计算公式;傅鹤林[8]也指出考虑迹长有界性失稳滑落的关键块体要比块体理论分析所得关键块体少得多,并表明体积较大的块体失稳的可能性较小,而临空面愈小的块体越易失稳;赵奎等[9]建立了块体的形成概率与结构面间距、迹长的理论公式,有效解决了小型结构面构成块体体积的问题;王英学等[10]、孙树林等[11]分别以结构面间距和块体三棱锥棱长来表征块体尺寸,研究了不同尺寸下块体的形成概率,后者还通过以块体形成概率对破坏概率进行加权得到的联合概率用来综合评价块体的稳定性;郝杰等[12]通过对有限迹长块体滑落概率的分析,对块体的安全系数进行了修正,结果表明修正后的块体安全系数有46.0%~66.4%的增幅。
上述研究均只是对完全贯通块体的形成概率和失效概率进行了研究,其默认结构面未完全贯通的岩体均为不可动的无限块体,即将岩体视为刚体,未能考虑到岩体在外力作用下的受拉破坏。假设三组结构面临近贯通岩体,可以判断被切割的岩体后端部面积很小,将承受很大的拉应力,当达到岩体的抗拉强度时,岩体则会在后端部发生拉张破坏而失稳,尤其是直接掉块时岩体的重力完全由端部的抗拉强度承受,岩体受拉破坏可能性将增大,而上述研究均未能考虑到岩体受拉破坏这种情况,只采用假定结构面完全贯通岩体的块体理论进行块体稳定性分析,这会导致失稳块体过多过大,无法为地下工程施工设计提供可靠的依据。
本文考虑了结构面长度的有限性,构建了岩体受拉破坏失稳的几何模型和力学模型,并采用Monte-Carlo法分析了潜在失稳块体的形成概率和失效概率。最后以黄岛地下水封洞库地下工程为例,分析了三组结构面在施工巷道不同部位潜在失稳块体形成概率和失效概率与岩体尺寸系数的关系,并对施工巷道不同部位形成的潜在失稳块体的失稳规模(即失稳体积范围)进行了预测评价,以为地下工程设计与施工提供依据。
1 未完全贯通岩体的失稳模型
块体理论假定空间上三组结构面和临空面(开挖面)完全切割岩体形成棱锥体,实则是认为任意两组结构面的交线长度不小于其所夹棱的长度,由于结构面的有限性,并不一定能完全切割块体,因此本文主要讨论未贯通岩体的稳定性分析模型,而完全贯通块体则是该模型的一种特例。
1. 1 潜在失稳块体的几何模型
切割岩体的结构面的几何形态采用1978年Baecher等建立的圆盘模型,这也是运用最广泛的结构面模型[13]。本文假定能发生失稳的岩体的形成条件为三组结构面在临空面上的迹线不小于所切割的三棱锥在临空面上各边的边长,这与赵文[7]、傅鹤林[8]和郝杰等[12]关于关键块体形成条件的假设相同。
当结构面迹线两端点与三棱锥在临空面上的顶点重合时,将对岩体造成最大程度的切割,即为最危险状态。以最危险状态分析,J1、J2和J3在临空面上迹线的两端点分别为A2和A3、A1和A3、A1和A2,其两两相交所形成三条交线的另一个端点分别为P1、P2、P3,由A1、A2、A3和P1、P2、P3构成的不规则棱台体即是潜在失稳块体的一般几何模型(P1、P2、P3三点重合时即为完全贯通的块体),如图1所示。下面求解潜在失稳块体的几何参数。
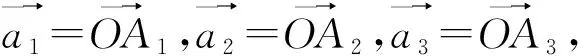

图1 潜在失稳块体的一般几何模型Fig.1 General geometric model of potentially unstable block
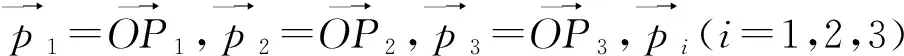
(1)
式中:bim和bin分别为Jm和Jn在棱线OAi上的截距长度。其中,b12的求解公式为
(2)
其他同理可得。
(2) 潜在失稳块体体积及各受力面面积。潜在失稳块体的体积V由下式计算:
(3)
块体在结构面Ji(i=1,2,3)上的面积Si为
(4)
式中:m、n为{1,2,3}中不为i的两个不同元素。
块体受拉面面积Sp及其内法线单位向量n分别由下面公式计算:
(5)
(6)
1. 2 潜在失稳块体的稳定性分析
地下工程中块体的运动有单面滑动、双面滑动和分离掉块3种模式,其中块体分离掉块一般发生在洞室顶板,块体单面滑动和双面滑动在洞室顶板和边墙均有发生。对于未完全贯通的潜在失稳块体,其后端(P1P2P3)发生拉破坏而与岩体分离,进而发生滑动(或掉块),如图2所示。
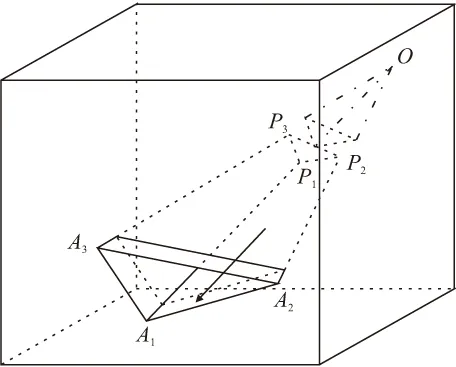
图2 潜在失稳块体的运动模式Fig.2 Motion mode of potentially unstable block
本文从几何学的角度来判断块体的运动模式,即以块体受到的重力G在各个结构面法向上进行投影,若结构面上产生非负压力,则块体沿该结构面滑动;若结构面上产生负压力(拉力),则块体与该结构面分离。块体沿结构面Ji滑动的判别式为
ni·nz≥0
(7)
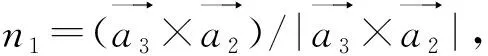
1.2.1 块体单面滑动

(8)
则块体单面滑动的安全系数计算公式为
(9)
式中:ζ为块体的安全系数;σt为岩块的抗拉强度(kPa);γ为岩块重度(kN/m3);ci和φi分别为结构面Ji的黏聚力(kPa)和内摩擦角(°);下同。
1.2.2 块体双面滑动

(10)
结构面Jm和Jn上块体受到的支反力Nm和Nn分别采用下面公式计算:
(11)
(12)

(13)
则块体双面滑动的安全系数计算公式为
(14)
式中:下标m和n均为块体滑动依附的结构面的编号;其他符号同上。
1.2.3 块体分离掉块
若三组结构面均不满足公式(7),则块体的运动模式为分离掉块,块体的运动方向即为块体重力方向,即
(15)
此时由于块体直接与各结构面分离而不产生滑动,块体的抗力则完全由块体后端部的抗拉力提供,则块体分离掉块的安全系数计算公式为
(16)
2 潜在失稳块体失稳体积的预测
岩体中结构面的空间分布极其错综复杂,多组结构面在不同的开挖段上可能形成的块体体积是不确定的。工程实际中为安全起见,通常采用最大块体体积作为设计基准,但这较为保守,因此本文提出一种修正的潜在失稳块体失稳体积的预测方法。
2. 1 修正的最大块体体积
对于给定产状的三组结构面与某一临空面切割岩体所能形成的三棱锥块体(不考虑结构面的有界性)具有相似性,由于临空面的有界性以及结构面间距的制约,将形成可能的最大三棱锥块体,其体积为Vm。
目前普遍使用Unwedge程序求解最大块体体积。该程序假定结构面贯穿研究区域,且在保持产状不变的情况下可任意移动,在分析时Unwedge程序会自动搜索出开挖面不同部位最大可能的三棱锥块体体积。工程实际中受结构面间距的影响,最大块体体积达不到Unwedge程序确定的最大块体体积。基于此,本文对最大块体体积进行了修正。
根据Unwedge程序获得临空面上4个顶点的坐标,据此求得临空面上各顶点与结构面J1、J2、J3的垂直距离分别为e1、e2和e3,对应三组结构面间距分别为d1、d2和d3,则结构面间距对Unwedge程序搜索的最大块体的修正比χ可用下式计算:
χ=min{d1/e1,d2/e2,d3/e3,1}
(17)
三组结构面间距均大于对应的垂直距离时,可能形成的最大块体即为Unwedge程序搜索得到的最大块体。
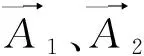
(18)
则最大块体体积为
(19)
2. 2 基于可靠性的潜在失稳块体的失稳体积预测
由于固定产状的结构面的空间位置仍具有不确定性,其切割岩体会形成各种尺寸的相似三棱锥块体,最大的块体即为上述修正的最大三棱锥块体。而且由于结构面直径的限制,其对不同尺寸的三棱锥块体有不同的切割程度(同一尺寸三棱锥块体可能被切割成不同体积的棱台体)。通过对不同尺寸的潜在失稳块体的形成概率和失效概率进行分析,可预测块体的失稳体积范围。
2.2.1 潜在失稳块体形成概率和失效概率的计算方法
能切割形成潜在失稳块体的结构面的直径应不小于所切割的三棱锥在临空面上各边的边长。采用ε来判断潜在失稳块体是否能形成,其表达式如下:
(20)
式中:li为块体在临空面与结构面Ji所夹的边长;Di为结构面Ji的直径;h(x)为阶跃函数,当x≥0时,h(x)取1,当x<0时,h(x)取0。
当ε=1时,能形成块体,即潜在失稳块体的形成概率Pe(即为ε=1的概率)为:
Pe=P(ε=1)
(21)
以安全系数ζ=1为块体稳定与破坏的界限,定义潜在失稳块体的失效概率Pf为
(22)
式中:f(ζ)为安全系数ζ的概率密度函数。
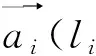
在块体失稳体积的不确定性分析模型中,一般选取Di为随机变量。结构面直径Di的概率分布函数一直是结构面研究领域的难题,2000年Zhang等[14]推导出由结构面迹长分布参数确定对数正态分布、负指数分布和伽玛分布型的结构面直径分布参数的求解公式,其中对数正态分布型结构面直径的分布参数为
(23)
(24)
式中:μl和σl分别为结构面迹长平均值和标准差的参数;μD和σD分别为结构面直径平均值和标准差的参数。
采用Monte-Carlo方法进行可靠性分析可以视作确定性分析模型的多次重复计算,该方法概念简单、直观,对于功能函数的非线性和复杂性没有任何要求,无需对随机变量进行正态化,且在样本量充足的情况下,可以获得高精度的失效概率估计值[15]。因此,本文选取Monte-Carlo方法计算潜在失稳块体的形成概率和失效概率。
在Matlab软件中输入参数μD和σD,即可生成结构面直径Di的随机数,利用下面公式计算形成概率μ和失效概率η的估计值:
(25)
(26)
式中:N为Monte-Carlo法随机模拟的总样本数;Ne为形成块体的总数;Nf为失效样本的总数,失效样本为安全系数ζ≤1的随机样本。
2.2.2 不同尺寸潜在失稳块体的形成概率和失效概率计算
以上述修正的最大三棱锥块体为基准,取尺寸系数k∈(0,1](k=1时对应修正的最大三棱锥块体),则当k取不同值时,三棱锥块体各棱长变为
(27)
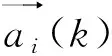
为契合基于随机抽样的Monte-Carlo法,需要将连续变量k进行离散化处理。考虑到地下岩体结构面在空间上分布的随机性和模糊性,即单个结构面在任意空间位置的可能性相等,故在连续区间k∈(0,1]中均匀抽取Nk个点,即
ki=i/Nk(i=1,2,…,Nk)
(28)

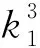
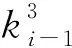
(29)
(30)
由此可计算得到潜在失稳块体不同体积下的形成概率和失效概率,以目标失效概率η0作为块体失稳体积预测的阈值,即可预测得到潜在失稳块体的失稳体积范围。
3 实例应用与分析
黄岛地下水封洞库地下工程包括施工巷道、主洞室、竖井和水幕巷道。2条施工巷道入口位于洞库南侧,设计标高均为70 m,分别沿洞库东西两侧向北延展,至洞库北端交汇;巷道走向为355°,终端设计标高为-30 m,平均坡降约为13.3%;巷道洞跨为9 m,洞高为8 m。
根据勘察资料,施工巷道围岩为二长花岗岩,发育多组结构面,岩体破碎—较完整。据统计,该区域内主要发育4组优势结构面,本文选取其中三组结构面进行研究。其中,结构面J1产状为86°∠52°,迹长服从对数正态分布,均值为1.16 m,标准差为0.16 m,间距约3.68 m;结构面J2产状为204°∠68°,迹长服从对数正态分布,均值为1.08 m,标准差为0.17 m,间距约5.54 m;结构面J3产状为140°∠83°,迹长服从对数正态分布,均值为1.36 m,标准差为0.23 m,间距约5.24 m。由3组结构面的迹长分布,根据公式(23)和(24)计算得到3组结构面直径的分布参数为:J1,μD1=1.42 m,σD1=0.27 m;J2,μD2=1.30 m,σD2=0.31 m;J3,μD3=1.67 m,σD3=0.34 m。岩体的物理力学参数见表1。

表1 岩体物理力学参数表
3. 1 最大块体体积的确定
根据深部岩体优势结构面和施工巷道几何形状参数,本文运用Unwedge程序对巷道围岩进行随机关键块体搜索,找出各个开挖面上可能出现的最大块体,其搜索结果见图3。
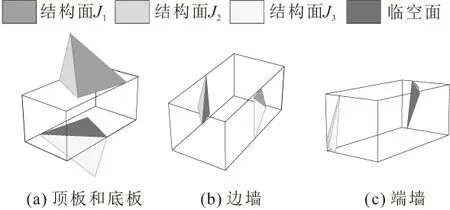
图3 Unwedge程序搜索的最大块体Fig.3 Largest blocks from Unwedge program
由Unwedge程序搜索得到施工巷道开挖面各部位最大块体的体积如下:巷道顶板和底板均为101.632 m3;巷道两边墙均为3.947 m3;巷道前后端墙均为1.307 m3。由于施工巷道前后端墙形成的最大块体体积很小,而底板上的块体为稳定块体,以下不再对其进行分析。
根据Unwedge程序获得棱锥体各顶点坐标,求得开挖面上各点到各结构面的垂直距离ei,再根据结构面间距并利用公式(17)和(18)对块体尺寸进行修正,最后利用公式(19)计算修正后的最大块体体积,从而得到施工巷道顶板、左边墙和右边墙上可能形成的最大三棱锥块体的修正结果,详见表2。
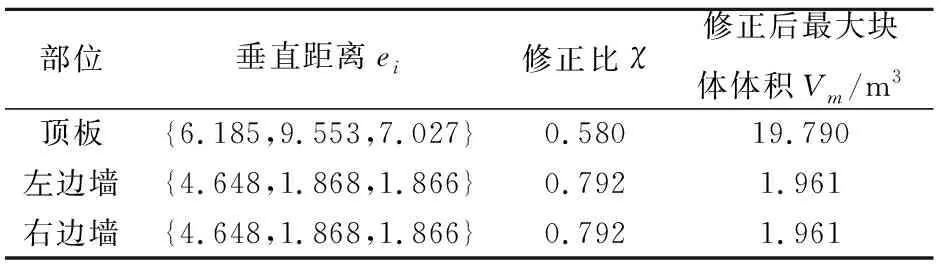
表2 施工巷道各部位可能形成的最大三棱锥块体体积的修正结果
3.2 不同尺寸潜在失稳块体的形成概率和失效概率计算与分析
对施工巷道顶板和两边墙上的块体分别进行可靠性分析,相似比(尺寸系数)ki以0.05的间隔在(0,1]上均匀取值,对应每一个值,对结构面直径进行10 000组随机抽样,计算潜在失稳块体的体积和安全系数,并记录。对于施工巷道顶板、左边墙和右边墙3个部位分别产生总数为200 000的样本量。
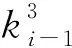

图4 不同尺寸潜在失稳块体形成概率的累积分布曲线Fig.4 Cumulative distribution curves of the formation probability of potentially unstable block of different sizes
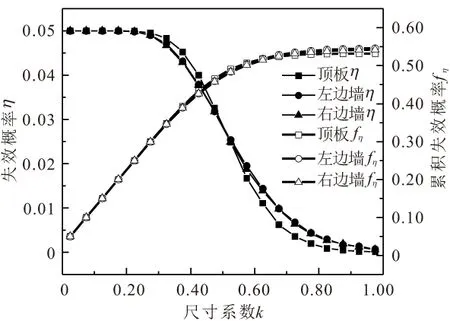
图5 不同尺寸潜在失稳块体失效概率的累积分布曲线Fig.5 Cumulative distribution curves of the failure probability of potentially unstable block of different sizes
概率密度形式的形成概率μ和失效概率η反映了不同尺寸潜在失稳块体形成概率和失效概率的相对大小,实际中裂隙岩巷道开挖过程中总是会形成各种尺寸的块体,μ和η无法反映其整体稳定性,累积形成概率fμ和累积失效概率fη分别表示小于某尺寸所有块体的形成概率和失效概率,可更贴合实际地反映结构面切割巷道围岩的稳定性。
3. 3 巷道围岩失稳体积的预测
参考陈祖煜等[16]的研究,对于大多数岩土工程问题,控制可靠度指标为3.10、对应破坏概率为0.001是合适的。本文以0.001作为目标失效概率η0,对施工巷道不同部位潜在失稳块体的失稳体积范围进行可靠性分析,其结果见表3。

表3 施工巷道不同部位潜在失稳块体失稳体积范围的可靠性分析
综上分析可知,结构面切割围岩在施工巷道上不同部位形成了潜在失稳块体,在巷道顶板上发生掉块失稳,巷道左边墙发生单面滑动失稳,巷道右边墙发生双面滑动失稳;以0.001作为目标失效概率,预测巷道顶板上发生失稳的最大块体体积为10.900 m3,巷道左边墙和右边墙上发生失稳的最大块体体积分别为1.681 m3和1.630 m3。该分析结果可为地下工程设计、施工等提供可靠的依据。
4 分析与讨论
(1) 现有研究关于块体的形成有以下两种判断方法:①结构面迹长大于棱锥底面各边长,如赵文[7]、傅鹤林[8]、郝杰等[12]提出的方法;②结构面直径大于棱锥各侧面外接圆直径,如孙树林等[11]提出的方法。将本文方法与上述两种方法作比较,以施工巷道顶板上的块体为例,分析不同尺寸潜在失稳块体的形成概率,得到各种方法的潜在失稳块体累积形成概率fu与尺寸系数k的关系曲线,见图6。
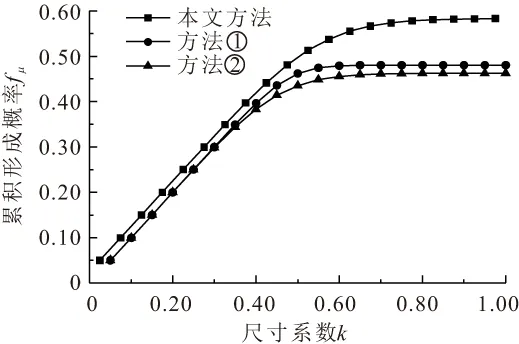
图6 不同方法潜在失稳块体累积形成概率与尺寸系数的关系曲线Fig.6 Relationship of the cumulative formation probability and the size coefficient of potentially unstable block by different approaches
由图6可见,潜在失稳块体的累积形成概率大小排序为:本文方法>方法①>方法②,即表明本文方法更安全可靠。
(2) 结构面间距限制了形成块体的最大尺寸,通过结构面间距修正比χ与Unwedge程序搜索的关键块体确定潜在失稳块体的最大体积。本案例结构面间距选取的是统计平均值,而实际上结构面间距是有一定变幅的。为了探讨结构面间距对上述可靠性分析结果的影响,本文以顶板块体为例,分别以结构面间距修正比χ=0.480和χ=0.680作两组重复随机计算(前述顶板块体χ=0.580),其计算不同结构面间距修正比下潜在失稳块体的失稳体积范围,结果见图7。

图7 不同结构面间距修正比下潜在失稳块体的失稳体积范围预测Fig.7 Prediction of the volume range of potentially unstable block with different correction ratios
根据目标失效概率为0.001,预测结构面间距修正比分别为0.480和0.680时潜在失稳块体的失稳体积区间,经计算分别为(0,10.514] m3和(0,11.145] m3,与前述χ=0.580时的(0,10.900] m3相差很小。而从累积形成概率来看,当χ=0.480、χ=0.580和χ=0.680时,巷道顶板上累积形成概率预测值分别为0.704、0.580和0.490,相差较大。
综上分析可知,结构面间距对潜在失稳块体失稳体积范围的预测结果影响较小,而对其累积形成概率有明显的影响,表现为结构面间距越小,累积形成概率越大;当χ=0.480时,预测得到的潜在失稳块体失稳体积最大值已临近可能形成的最大块体体积,且当结构面间距更小时,最大块体体积的预测值将完全由结构面间距控制。
5 结 论
由于结构面长度的有限性,地下岩体被切割形成完全贯通岩体和未完全贯通岩体,后者中一部分为可能发生后端受拉破坏而失稳的棱台形块体。本文以完全贯通块体和上述近棱台形块体作为可能失稳的潜在失稳块体,建立了潜在失稳块体的几何模型和力学模型,推导出潜在失稳块体安全系数的计算公式,并给出了一种预测潜在失稳块体失稳体积范围的预测方法,即:该方法首先根据开挖面尺寸和结构面间距求得三组结构面可能形成的最大棱锥体;然后再运用Monte-Carlo法分析不同尺寸潜在失稳块体的形成概率和失效概率的变化规律;最后以目标失效概率为阈值预测潜在失稳块体的失稳体积范围。
本文通过运用上述方法对黄岛地下水封洞库施工巷道潜在失稳块体进行可靠性分析,并研究了结构面直径呈对数正态分布的三组结构面在巷道各部位切割形成潜在失稳块体的形成概率和失效概率与岩体尺寸系数的关系,结果表明:岩体尺寸系数越大,潜在失稳块体的形成概率和失效概率越低。以0.001的目标失效概率预测了施工巷道各部位潜在失稳块体的失稳体积范围,结果为:巷道顶板为0~10.900 m3,预测左边墙为0~1.681 m3,巷道右边墙为0~1.630 m3。同时,还讨论了结构面间距对潜在失稳块体失稳体积范围预测结果的影响,结果表明:当结构面间距修正比大于0.48时,对预测结果无明显影响;当结构面间距修正比小于0.48时,其对预测结果有控制作用。此外,将本文方法与已有方法的预测结果进行了比较,结果表明:本文方法获得的预测结果是安全可靠的,该预测结果可为地下工程设计、施工等提供可靠的依据。
