非球面折反射全景成像系统设计

（长春理工大学 光电工程学院，长春 130022）

近年来，随着机器视觉、VR等应用领域的日益发展，在生活中需要采集的图像信息也越来越丰富，而传统相机的成像视场就存在了一定的局限性，为了解决传统相机视场角狭窄的问题，360°全景相机应运而生［1］。全景成像技术从80年代起，就受到越来越多的国内外研究学者的关注，他们对此作了大量的工作与研究，并且也取得了一定的研究成果。在视频监控和安防领域中，日本Sony公司的专利Desktop Model RPU-C251中，就引入了折反射全景成像技术，Conroy L等人研究了使用两个反射镜与相机配合组成的立体视觉系统［2］。浙江大学课题组对折反射相机模型进行了研究，并提出全景凝视成像的方法，获得了成像视场角为180°的图像［3］。Christopher Mei等人研究了单视点全向平面栅格的全景成像相机的标定方法［4］。北京理工大学课题组通过设计双曲面反射镜实现了全景成像［5］。哈尔滨工业大学的研究小组对一个带有凹面反射镜的圆柱形成像系统进行了设计与分析［6］。

目前，全景成像的实现方式主要有以下四种：多图像拼接技术，鱼眼镜头，环视透镜系统，折反式光学系统［7］。折反式全景相机是近几年发展起来的一种新的环型全景成像形式，与旋转式扫描相机、多图像拼接相机和鱼眼相机相比，在很多方面都具备显著优势：尺寸小、结构灵活简单、成本低廉、实时性好［8-9］。

折反射全景相机主要由三部分组成，即曲面反射镜、成像透镜组和CCD相机。它与鱼眼镜头折射的方式不同，鱼眼镜头是通过折射来压缩视场角，折反射相机是利用曲面反射镜对水平方向入射的光线进行收集与压缩，并转入到后面的成像系统中，进而获得360°环视全景成像的效果。折反射全景成像系统分为单视点和非单视点两类，单视点成像表示进入系统时的入射光线的延长线有唯一交点，它符合针孔相机模型，不然即为非单视点成像。跟非单视点系统相比，单视点系统的物像映射关系比较容易，根据单视点成像的约束条件可以计算出镜面的特定曲面面型，并且部分计算机视觉理论和算法均适用该类成像系统。而非单视点成像的面型求解就比较麻烦，它需要用不同的投影方法去获得，最后再用高阶方程的拟合求解镜面的曲面方程［4］。

为了实现视场清晰的折反射全景成像系统设计，不仅要对球差、彗差、色差等影响成像质量的像差进行校正以外，还要对系统产生的畸变进行特殊的控制。在折反式系统中，反射镜面型的设计就对畸变的控制起到了关键性的作用。因此，利用单视点折反射全景成像的理论思想，设计了一款高阶非球面反射镜和常规成像透镜组相机相结合的系统，有效控制了畸变对镜头的影响。系统的视场角为360°×（-50°～15°），畸变量在50%以下。

1 折反射全景成像系统的设计

1.1 折反射全景成像系统尺寸的计算

系统的外形尺寸主要由反射镜离摄像头的距离h和反射镜的口径D决定，如图1所示，曲面反射镜一般是以光轴旋转对称的，像素平面为长方形，取像素平面的短边所在的剖面进行分析。dmin是像素平面短边上的有效像素点到图像中心点的最短距离，f为透镜的焦距，通过反射镜压缩后的视场角为θ：

式（1）表示了折反射全景系统中的系统尺寸、CCD尺寸和视场角之间的关系，设计系统时根据应用要求选取合适的摄像头和视场角，标定出dmin和透镜的焦距f，并确定合理的反射镜口径D和反射镜到摄像头的距离h。

图1 折反射全景成像系统的尺寸关系

1.2 单视点成像的几何分析

本节以单视点结构为约束进行讨论，以双曲面反射镜为例，推导了满足单视点约束并且采用双曲面反射镜的系统结构参数。符合单视点约束的系统反射镜都具有两个焦点F1点和F2点，一个位于反射镜面的内侧F1处，另一个则在反射镜外侧F2处，两个焦点的光学性质就是入射光线经过F1，反射光线经过F2，如图2所示。全景相机的投影中心C点与F2相重合，则光线穿过C点，投影在探测器上。单视点折反射全景系统由C点和F1两个点共同约束，可以建立类似传统成像的透视投影模型，进而计算出系统的设计参数。

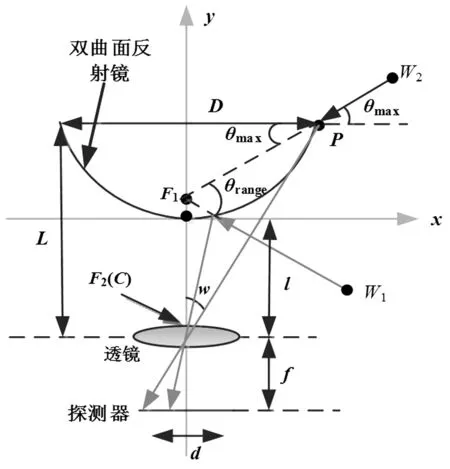
图2 单视点折反射全景成像系统结构图

图中l为反射镜顶点O与投影中心C点之间的距离，L定义为反射镜与透镜组的距离约束，e代表圆锥曲线离心率。该坐标系下的双曲线可表示为：

由三角相似关系可以得出：

其中，D为反射镜口径，f为反射镜的焦距，d为探测器尺寸。

最大俯角θmax的正切值为：

由于P点在双曲线上满足（2）式，在已知D和f的情况下，L可以直接由（3）式解出，（3）和（4）式联合得到（5）式，l和e可以由（1）和（5）联立解出。

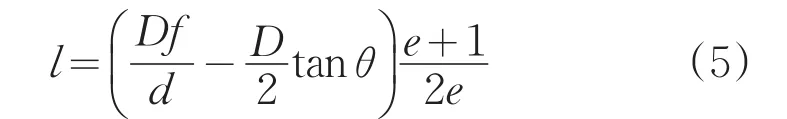
利用求得的参数值就可以设计出满足特定的像面尺寸和视场角的折反射全景成像的系统结构。在单视点约束的结构下，通过优化折射透镜组的参数便可以实现全视场的清晰成像。

2 实验及结果

基于以上系统参数的计算方法，本文设计了一套高阶非球面折反射全景成像的光学系统。整个镜头可以满足大于800万像素的分辨率，镜头焦距f为0.7mm，水平全视场角达到360°，俯角-50°，仰角15°，其光学总长度小于45mm，光学的最大口径小于25mm。

系统中采用了高阶非球面作为反射镜，大大降低了系统镜片的数量，透镜组采用球面设计，可以通过优化系统来矫正各种像差，并且为了更好地矫正色差和球差，在透镜组中引入两组双胶合透镜。在折反射系统中，对于成像分析的需要，非球面透镜的引入可以提高成像质量，因此反射镜的面型就起到了关键性的作用，以下是高阶非球面的数学表达式：

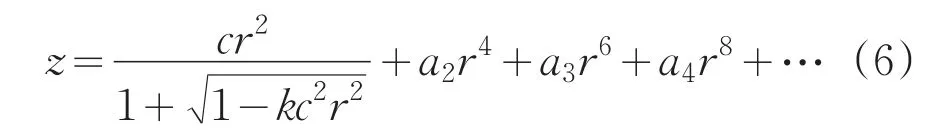
通过最小二乘法拟合出实验设计结果的高阶非球面的各项系数如表1所示。

表1 高阶非球面方程系数

根据参数的选取和优化，利用Zemax软件进行光线追迹得到的系统光路图和成像质量分析如图3-图6所示。

其中，从图4可知探测器的频率在120p/mm处以内的MTF均在0.2范围内，从而可以满足该系统成像的要求。从图6的点列图可以看出该镜头的各视场的弥散斑半径均在8mm以内，可以初步判断系统处于衍射极限状态。以上的成像性能结果都可以证明该系统具有较好的成像质量，符合设计的要求。

图3 系统的光路图

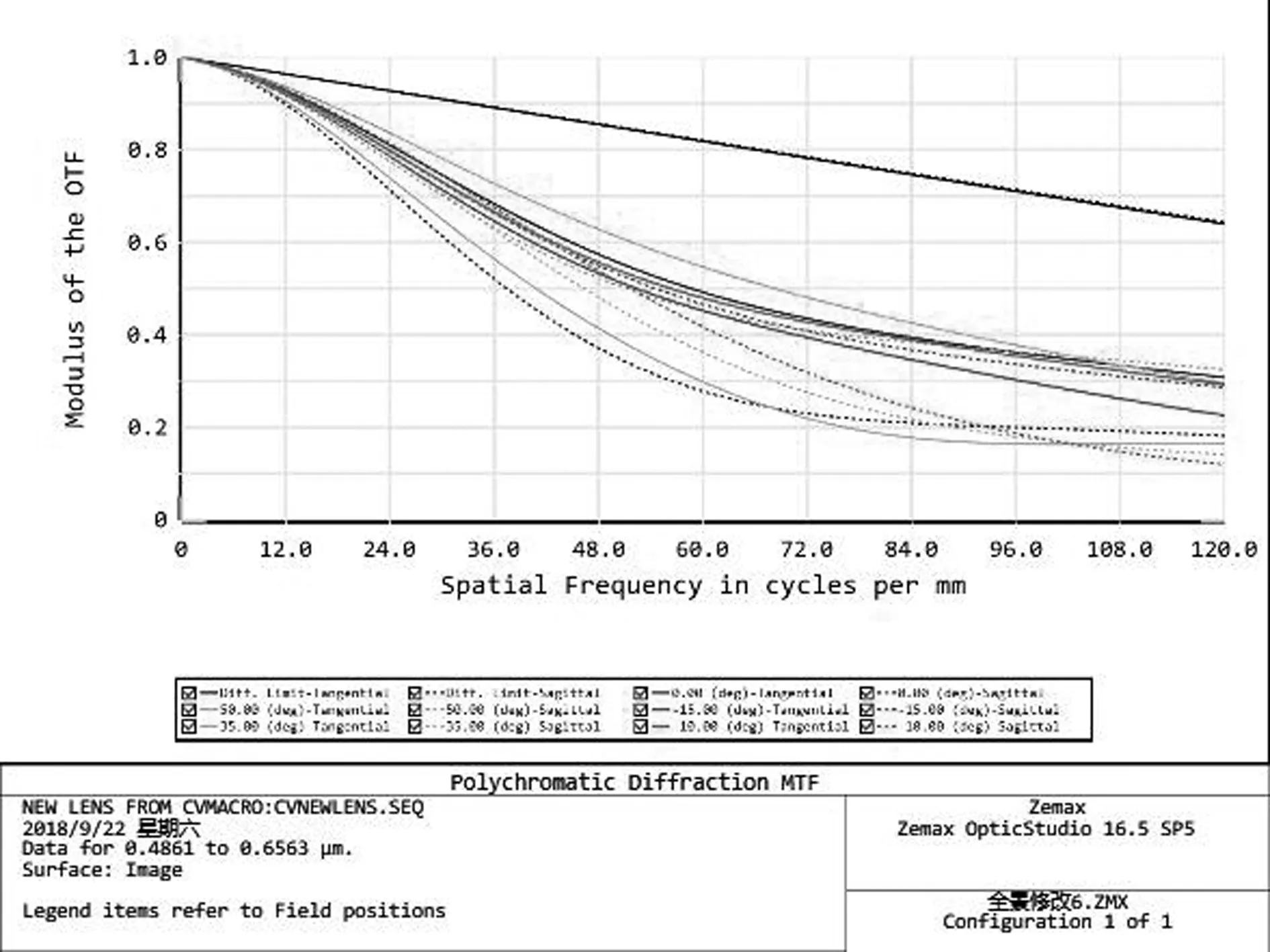
图4 调制传递函数（MTF）曲线图

图5 场曲和畸变图

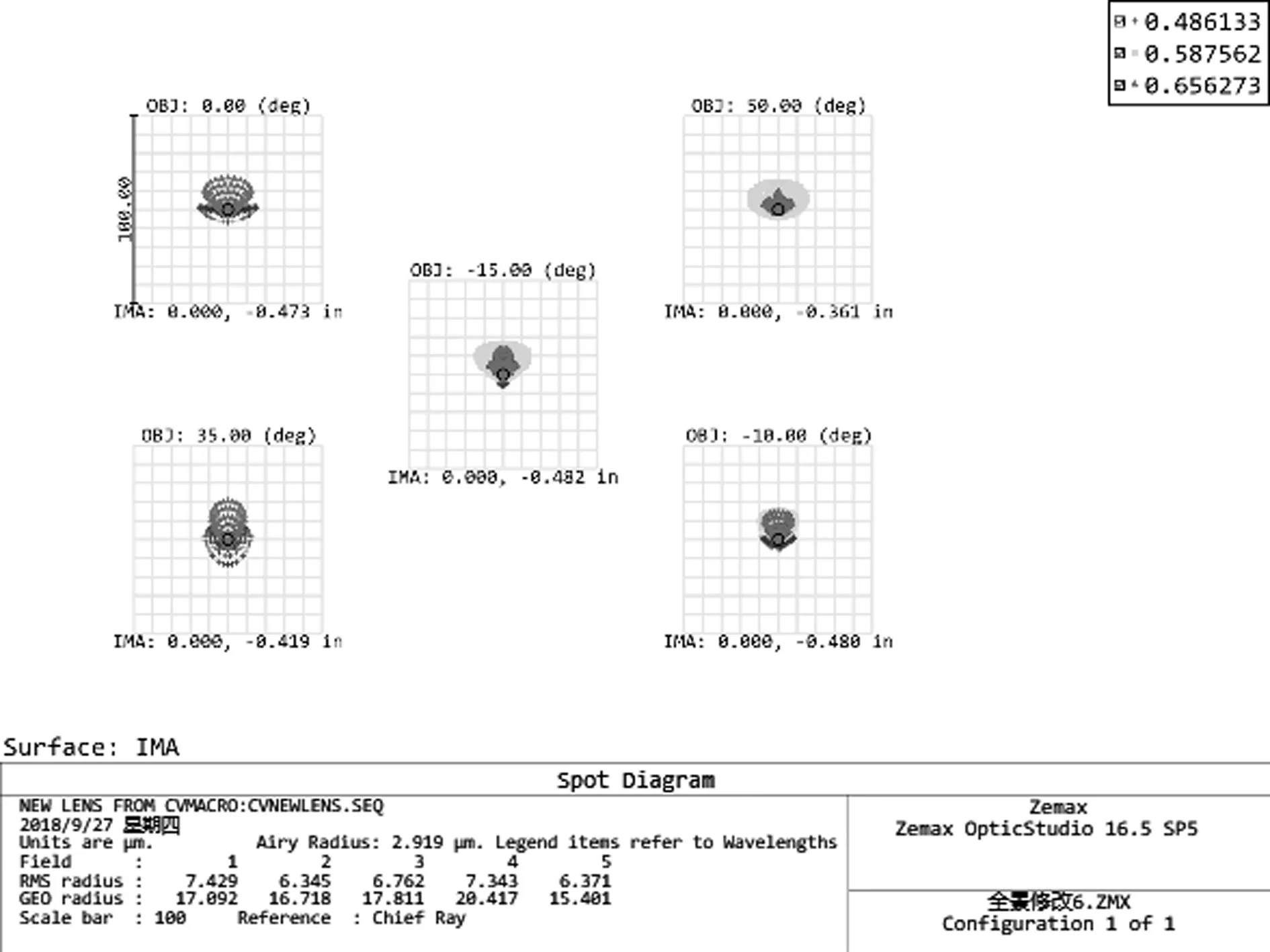
图6 点列图

3 结论

本文除了对全景成像技术做了简单的概述外，还对单视点折反射式的全景成像系统进行了详细介绍与理论分析。通过反射镜与成像透镜组的相结合，有效矫正了系统的像差，同时通过设计一款全新的高阶非球面，解决了折反式全景镜头对于畸变的控制问题。系统的视场角达到了360°×（-50°～15°），探测器的频率在120p/mm处以内的MTF均在0.2范围内。该系统在安防监控，智能家居以及车载影像领域均具有广阔的应用前景。