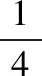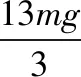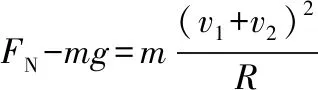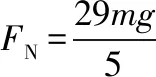弧形槽类连接体模型动量和能量问题探究及分析策略
2019-04-24四川
四川 王 敏
巧用合成分解,突破动量守恒。
教育部考试中心为高考命题“最新定调”,指出物理学科通过将动量和近代物理作为必考内容进行考查,完善学生的知识结构,为学生解决问题提供更多有力工具,有利于学生更好地认识实际现象,理解更深层次问题。动量守恒定律和机械能守恒定律的综合应用是近年高考的重点,也是学生理解和运用的难点,本文从学生在处理弧形槽类连接体模型时常见的疑惑入手,巧妙运用运动的合成和分解的方法,分析水平方向动量守恒问题,以及从做功和能量的角度分析系统机械能守恒问题,让学生准确理解和恰当运用。
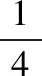
( )

图1
A.小球可能从圆弧轨道上端抛出而不再回到小车
B.小球不可能离开小车水平向左做平抛运动
C.小球不可能离开小车做自由落体运动
D.小球可能离开小车水平向右做平抛运动
【问题探究】1.为什么小车和小球组成的系统动量不守恒,而只是水平方向动量守恒?
3.为什么以小球或小车为研究对象,机械能不守恒?但对二者组成的系统为研究对象,机械能是守恒的?
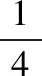
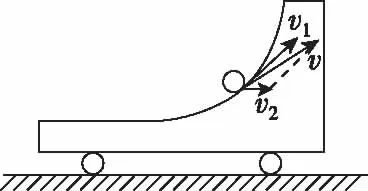
图2

图3
若小球不能抛出,说明小球在竖直方向上的速度为0,那么v1必然为0,因此二者在水平方向应共速,此时两物体相对速度为0。
3.对小球而言,除重力之外还受到小车对它的支持力FN,其方向与相对速度v1的方向垂直,但与小球的速度v的方向成钝角(如图4所示),则支持力对小球做负功,小球的机械能减少;反作用力FN′(压力)作用在小车上,其方向与小车速度v2的方向成锐角(如图5所示),对小车做正功,小车的机械能增加。所以单独对小球和小车为研究对象,机械能不守恒。

图4

图5
以系统为研究对象,因系统内的弹力在垂直于接触面方向的相对位移为0,系统内弹力做功代数和为0,故系统机械能守恒。或者从能量的转化和守恒定律来看,系统没有其他能量参与,故系统机械能守恒。
【例题解析】由以上分析可知,当小球从圆弧冲出时,小球做斜抛运动(以大地为参考系),因为水平方向上小球与小车速度相同,于是水平方向上二者在相同的时间内有相同的水平位移,因此小球将会回到小车上,从小车左端离开。
当二者分离时速度分别设为v3、v4,由系统水平方向上动量守恒定律(取水平向右为正方向)可得
mv0=mv3+Mv4①
系统除重力之外没有其他力做功,故系统机械能守恒
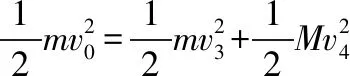
由以上两式可解得


由③式可知,当m 当m=M时,v3=0,小球做自由落体运动; 当m>M时,v3>0,小球向右做平抛运动。 由以上分析可得,正确答案应为D。 【答案】D 【小试身手】 【重庆巴蜀中学月考试题改编】(多选)如图6所示,将一光滑的质量为4m、半径为R的半圆槽置于光滑水平面上,在槽的左侧紧挨有一个质量为m的物块,今让一质量也为m的小球自左侧槽口A的正上方高R处从静止开始落下,与半圆槽相切自A点进入槽内,则以下结论中正确的是 ( ) 图6 A.小球在半圆槽内第一次由A到最低点B的运动过程中,槽的支持力对小球做负功 B.小球第一次运动到半圆槽的最低点B时,小球与槽的速度大小之比为4∶1 【解析】从A→B的过程中,小球对半圆槽的压力方向向左下方,所以半圆槽要向左推动物块一起运动,因此小球参与了两个运动:一个是沿半圆槽的圆周运动,另一个是与半圆槽一起向左运动,小球所受支持力方向与速度方向并不垂直,而是大于90°,故槽的支持力对小球做负功,A正确; 由小球、半圆槽和物块组成的系统在水平方向不受外力,故球、半圆槽和物块在水平方向上动量守恒,取向右为正,则有 mv1-(4m+m)v2=0 ① 解得v1∶v2=5∶1 ② 根据系统机械能守恒得 小球第一次在最低点,由牛顿第二定律得 小球在半圆槽的右侧运动时,小球对半圆槽的压力方向向右下方,半圆槽做减速运动,物块与半圆槽分离,小球与半圆槽水平方向动量守恒,当小球从右侧C点抛出时二者水平方向共速,设为v。取向右为正,有 mv1-4mv2=(m+4m)v⑦ 综合上述分析,正确答案为AD。 【答案】AD 【扩展】小球第一次从半圆槽右端C点抛出时,上升的高度是多少? 【解析】以小球和半圆槽为系统,在从半圆槽B点到小球上升到最高点的过程中,系统机械能守恒,则有 由⑩式可看出h 对以上弧形槽模型的分析方法可扩展到由轻绳连接的连接体机械能守恒和水平方向动量守恒问题,如下: 【模型扩展】如图7所示,在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5 kg的光滑金属圆环,轻绳一端拴在环上,另一端系着一个质量为M=1.98 kg的木块,现有一质量为m0=20 g的子弹以v0=100 m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间,g取10 m/s2),求: ①圆环、木块和子弹这个系统损失的机械能; ②木块所能达到的最大高度。 图7 【分析】①子弹射穿木块的过程遵守动量守恒,由动量守恒定律求出子弹穿入木块后子弹和木块的共同速度。即可求得系统损失的机械能; ②木块向右摆动的过程中,圆环向右滑动,此过程中,系统水平方向不受外力,水平方向的动量守恒。当两者水平速度相同时向右摆到最大高度,由系统的水平方向动量守恒和机械能守恒结合求解木块向右摆动的最大高度。 【解析】①子弹射入木块过程,系统的动量守恒,取向右方向为正方向,根据动量守恒定律得 m0v0=(m0+M)v1 机械能只在该过程有损失,损失的机械能为 ②木块(含子弹)在向上摆动过程中,以木块(含子弹)和圆环组成的系统为研究对象,根据系统水平方向的动量守恒得 (m0+M)v1=(m0+M+m)v2 根据机械能守恒定律有 代入数据可解得h=0.01 m