基于RS属性约简与LS-SVM的装备研制风险综合评价

黄海清，甘旭升，曲 虹，董 鑫

（1.西京学院，西安 710123；2.空军工程大学空管领航学院，西安 710051）

0 引言

在过去20年～30年中，美国在武器装备研制过程中，由于对风险估计不足或不够精确，导致实际费用超出预算近四成，并大幅拖延了研制进度。鉴于此，美国国防部将风险评价贯穿于装备研制全过程，并视其为评审的重要内容。在国内，针对装备研制风险综合评价问题也进行了有益的尝试和探索。张松昌等采用模糊层次分析法对某型陆战装备的研制风险进行了综合评价，以克服人为主观偏好造成的模糊性[1]。宋春雳等将熵权双基点法应用于装备研制风险评价中，解决了传统评价中依靠主观经验确定权重的问题[2]。此外，迟宝山、吴亚雷、陈士涛等也进行了深入分析与研究[3-5]。这些方法虽然部分解决了风险的定量评价问题，但其中的一些边界参数较难确定，得到的评价结果存在分类不够精细、区分性不强等问题。此外，还有些方法将问题简单分解为若干小部分，将复杂风险简单化，既缺少理论依据，也没有作数值分析，因此，有必要研究和探寻更为有效可行的装备研制风险综合评价方法。

基于以上分析，本文针对装备研制的特点，构建了风险评价指标体系，并在集对分析（Set Pair Analysis，SPA）法构造评价样本基础上，提出基于粗糙集（Rough Set，RS）属性约简的最小二乘支持向量机（Least Square Support Vector Machine，LS-SVM）的装备研制风险综合评价方法，即RS-LS-SVM，旨在为有效管控新型装备的研制风险提供新方法。

1 装备研制风险评价指标体系

武器装备研制风险评价体系是指由各方面相互联系、能敏感地反映武器装备研制的状态及存在问题的具体指标构成的有机整体。在设计风险评价指标体系时，应该从分析影响因素入手，根据研制中暴露出的问题特点，参照相关研究成果，征求专家的意见，选取具有代表性的评价指标，并兼顾指标测量问题，以客观地对武器装备研制风险进行科学评价。通过对武器装备研制实践的概括与总结，本文构建了如图1所示的武器装备研制风险评价体系，重点研究环境、政府、生产、研发、财务和管理对于研制风险的影响，以期通过风险评价来确认解决方案或建议的正确性和可操作性，使武器装备研制趋于正规化和标准化。

2 粗糙集属性约简

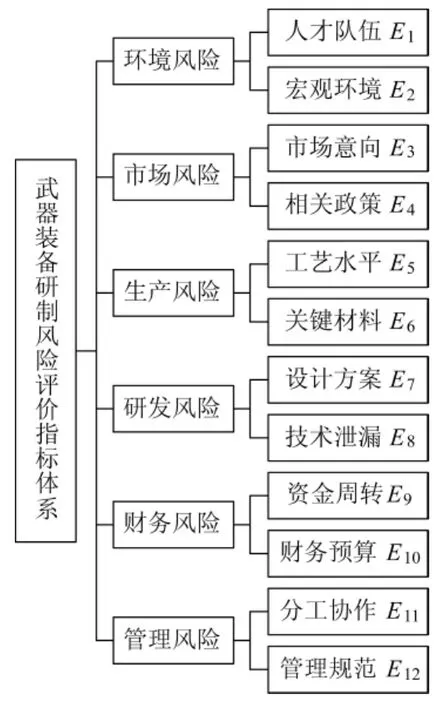
图1 装备研制风险评价指标体系

RS理论认为，知识必须以对象的分类能力为基础，分类过程中差别较小的对象被纳入一类，对象与对象之间形成的关系被称为不可辨识关系。约简是RS的核心问题之一。对于较复杂问题，通过在约简中加入启发式信息，能够缩小问题的搜索空间。本文研究了可辨识矩阵（可以标识决策属性和条件属性之间关系的矩阵）的约简，并在属性重要性基础上，引入一种以属性频率作为启发式信息的属性约简算法[6]。

设决策表S=（U，A，V，f），R⊂C，则任意属性a∈C-R的重要度可定义为SGF1（a，R，D）。本文采用的属性频率约简算法，是将可辨识矩阵中属性a出现次数作为判断属性重要性的标准，即SGF1（a，R，D）=p（a），并将其视为属性相对于决策重要性的启发式信息。该方法按照属性对分类的影响选择属性，当属性重要性相等而无法选择属性时，可引入一种以M值作为标准的属性重要度方法。

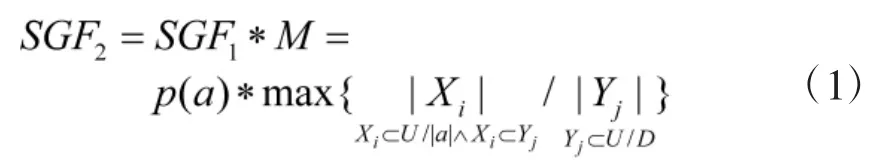
式中，SGF2表示属性a分类中包含决策属性分类Yj的最大对象数相对分类Yj的比例。如果条件属性集决定的等价类中有一个是Yj的子集，虽然不存在决策类的子集，条件属性集对Yj仍很重要，SGF2就是在此基础上提出的。对于重要度相同的属性，可计算它们的M值，并选择最大M值对应的属性加入到属性约简集中。则基于属性重要度的约简算法的流程如下：

输入：决策表S=（U，C U D）；

输出：S的属性约简集。

1）计算可辨识矩阵，将该矩阵中的核属性（属性组合数为1的条件属性）赋给约简后的属性集，即red=Core；

2）删除可辨识矩阵中含有核属性的属性组合项；

3）计算可辨识矩阵中所有剩余条件属性的出现频率，选出频率最高的条件属性a，即red=red U{a}。若属性的出现频率相同，则计算属性M值，并选取最大M值对应的属性加入red中，删除可辨识矩阵中包含a的属性组合项；

4）计算POSred，当POSred（D）≠POSC（D）时，转入步骤3），当POSred（D）=POSC（D）时，red即为最后约简集，其中，POSred（D）表示根据约简集red中条件属性，一定能归入决策类D的所有对象集合。

由于数据采集的不完整性和不规范性，在RS属性约简前，需要预先对条件属性中的连续属性进行离散化。其基本思想是根据需要将连续属性值划分为几个子区间，然后利用这些子区间代替原有的实际值，从而使决策表泛化，能够用于RS约简计算。本文采用等距离划分方法，该方法离散化时在取值域按等距离分割，并不考虑条件属性与决策属性之间的依赖关系，当然，也可根据需要，选取考虑条件属性与决策属性之间依赖关系的离散化方法，如基于熵的离散化方法。

3 LS-SVM模型

LS-SVM是支持向量（SVM）的一种改进版本，即将二次规划问题转化为线性方程组问题来求解[7]。

设训练集（{xi，y）i|i=1，2，…，n}，输入向量xi∈Rd，输出 yi∈R，n为样本数，d为输入维数。通过一个非线性函数将样本从原空间Rd映射到某个特征空间中，并在该特征空间中引入结构风险函数构造最优函数，其中，b为常数。此过程可描述为如下约束优化问题

式中，正则化参数C用以平衡经验风险和置信范围。ξi为非相关随机误差。

对于以上约束优化问题，可通过Lagrange乘子法进行处理，其中，Lagrange乘子法是一种寻找变量受一个或多个条件所限制的多元函数的极值方法。则式（2）和式（3）可转化为

式中，αi为 Lagrange乘子。

考虑到KTT条件是不等式约束的最优化问题的最优性条件（最优解的性质）。利用KTT条件可将上式得转化为等式形式，并通过最小二乘法求解αi和b，得到线性模型，其中，则有

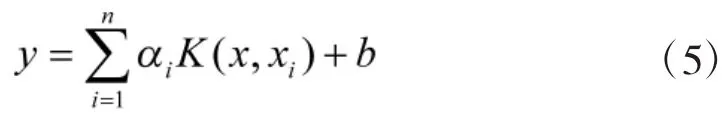
为保证LS-SVM泛化性能，参数C和σ2需要采用k-折交叉验证法与网格搜索法优化。k-折交叉验证法将训练样本随机等分为k个相同子集，取k-1个子集作为训练集，训练LS-SVM估计模型式（5），剩余的一个子集作为测试集，将测试集输入xi代入式（5），得到输出估计。如此不重复循环k次，直到各子集都作为测试集被验证一遍，然后计算出均方误差（Mean Squared Error，MSE）。网格搜索法将C和σ2所在区间等间隔划分为P个点和Q个点，形成一个网格，其交叉点即为P×Q个参数组合。在k-折交叉验证法基础上计算出各参数组合的MSE，最小MSE对应的参数组合即为最优参数。若不满意，可将上次较小MSE对应的参数组合进行特征分解，提取特征值和特征向量，重新定义更精细的网格进行搜索验证，直到找出满意的参数组合。

4 装备研制风险RS-LS-SVM评价模型

由于装备研制过程具有动态性、模糊性的特点，各类风险指标之间的作用关系也比较复杂，要理清各指标之间的耦合关系极为困难。在装备研制风险评价模型中，其评价指标体系是由专家访谈、前人研究经验所确定的，并不一定完全合理，可能存在一定冗余，进而影响到评价效果。若预先根据采集到样本进行RS属性约简，以消减影响较小的冗余指标。基于此，本文提出的装备研制风险的RS-LS-SVM评价过程如下页图2所示。该过程大致可分为3部分：首先，在评价指标数据基础上利用SPA法构造样本；然后，通过RS前置处理，对评价指标进行属性约简；最后，根据RS约简结果，构建装备研制风险的LS-SVM评价模型，并完成评价。

在图2评价流程中，SPA法通过引入联系度概念统一处理模糊、随机、中介和信息不完全导致的不确定性。其核心思想是先对不确定性系统中的两个有关联的集合构成集对（集对是指具有一定联系的两个集合组成一个对子），再对集对的特性进行同一性、差异性和对立性分析，最后建立集对的同、异、反的联系度[8-9]。根据装备研制的过程及其风险特点，构造出指标U的风险评价等级对应的联系度函数，如表1所示。

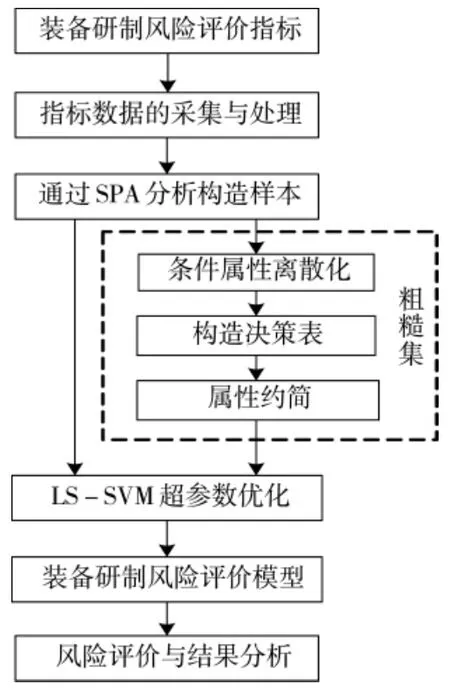
图2 装备研制风险RS-LS-SVM评价过程

表1 装备研制风险评价等级及其联系度函数

表中，x为指标的评价分数值；U0～U5为评价指标各等级的界限值。第i个指标的第j个等级的联系度为μij（j=1，2，3，4，5），若ωi为各指标的权重，即可计算出各指标第j个等级的总联系度。最大总联系度对应的等级就是最终风险评价等级。

5 案例分析

确立了装备研制风险的评价指标体系和评价流程后，就可以结合研制实际进行风险建模与评价。为验证方法的有效性，本文以空军某型号雷达研制项目的风险评价为研究对象，该型雷达主要用来搜索、截获和跟踪空中目标，并提供武器瞄准、射击和制导所需要的数据。

5.1 SPA法构造样本

评价所用到的原始数据，来源于研制单位、使用单位、协作单位以及装备机关的10位有关专家打出的评价分数，并作了必要的数理与脱密方面的预处理，如表2所示。整个案例分析，更多地从演示角度，阐明所提出方法用于评价装备研制风险的整个过程。

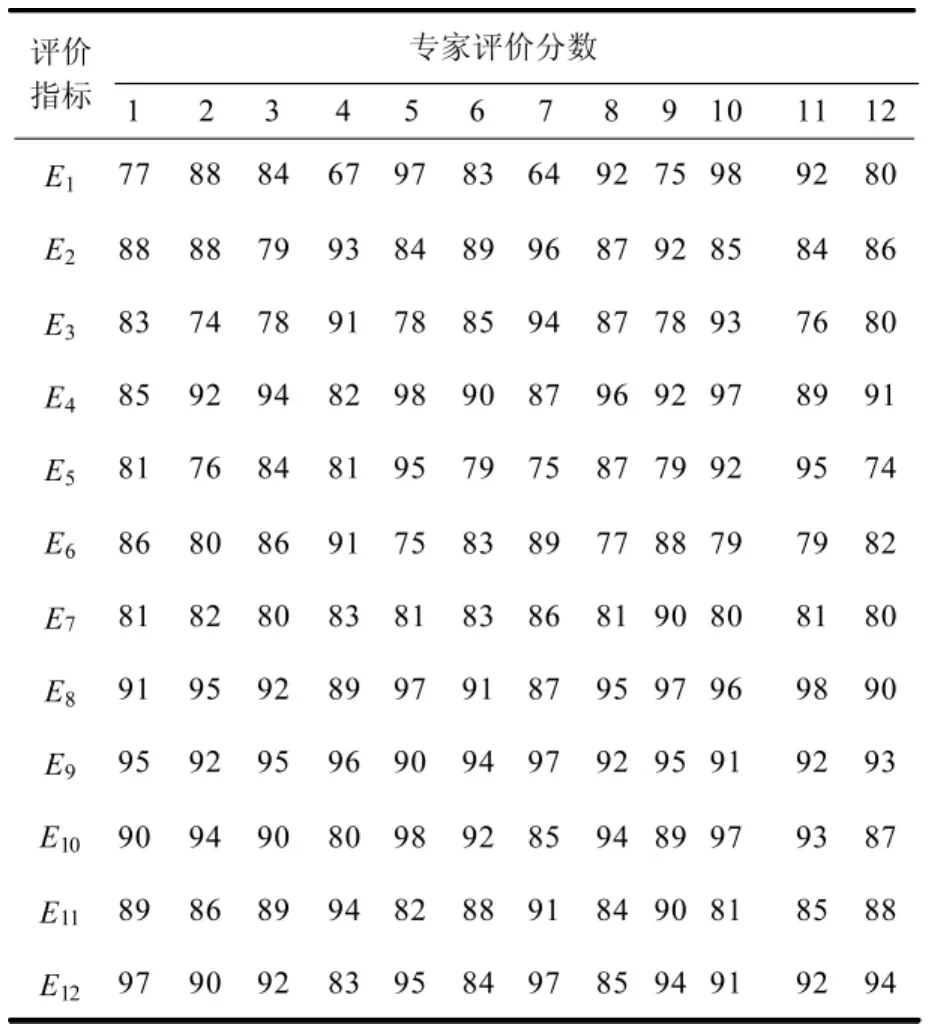
表2 装备研制风险各指标的专家评价分数

首先，确定各评价指标的风险等级区间。例如，对于市场意向 E3来说，数值 50，60，70，80，80 分别表示市场意向等级：I介于[0，50]区间，II介于（50，60]区间 ，III介于（60，70]区间，IV介于（70，80]区间，V 介于（80，100]区间，其他评价指标的等级区间都依此过程给出。然后，通过层次分析法确定各评价指标的权重，ω1，ω2，…，ω12分别为：0.042，0.069，0.079，0.093，0.173，0.057，0.087，0.035，0.082，0.092，0.135，0.057。最后，基于 SPA 法计算出各组专家分数的评价结果。将评价指标E1～E12对应的一组专家评价分数代入表1中的联系度函数，并结合权重计算出这组专家分数的5个总联系度值，进而由最大值确定这组专家评价分数的风险等级，其他各组评价分数如此类推，得到的SPA评价结果如表3所示。通过以上SPA过程，结合表2及表3的评价结果，通过标准化处理即可构造RS-LS-SVM的输入输出样本，并将编号1～10样本用于模型训练，编号11和12样本用于测试。所涉计算在LS-SVMlab1.5工具箱基础上通过MATLAB编程语言实现。

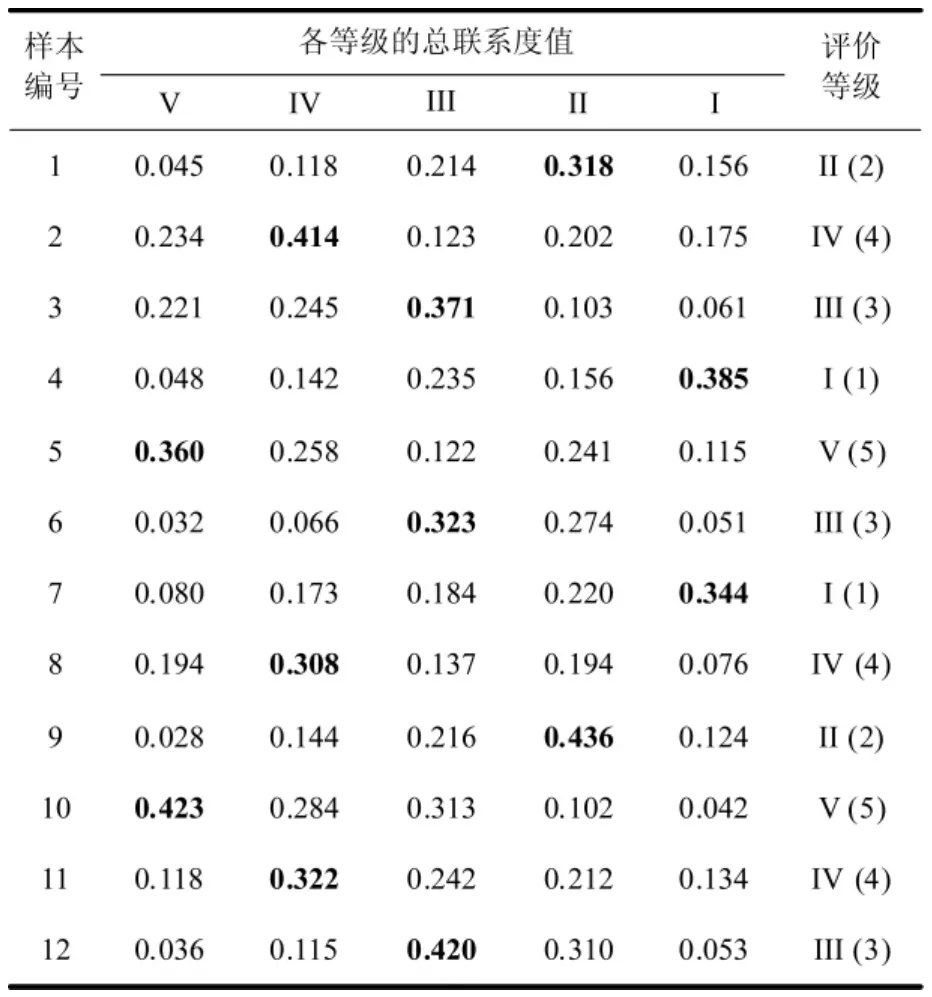
表3 装备研制风险的SPA评价结果

5.2 RS前置处理

在进行RS属性约简前，先要通过等距离划分法对训练样本进行离散化。只有完成离散化处理，才能将各评价指标作为条件属性，将SPA评价结果（评价等级已作数字化处理）作为决策属性，构建决策表，进而基于属性重要性对决策表进行属性约简，其最小约简后的决策表如表4所示。从表中可知，最小约简属性集为{E1，E3，E5，E6，E7，E10，E12}。也就是说，这7个条件属性（评价指标）相对于决策属性为核心属性，是不可省略的，而条件属性E2，E4，E8，E9和 E11是冗余的。

5.3 LS-SVM建模与评价

将评价指标 E1，E3，E5，E6，E7，E10和 E12对应的训练样本（非离散化）作为输入输出，对LS-SVM评价模型进行训练。

训练前，采用10-折交叉验证法和网格搜索法对超参数C与σ2寻优。两参数的初始值可分别设为不同值，交叉验证的初始化分组数为5。由于C与σ2数量级相差较大，寻优过程包括粗选和精选两个步骤：粗选格点数10×10，用“·”表示，搜索步长较大，采用误差等高线确立最优参数范围；精选格点数仍为10×10，用“×”表示，在粗选基础上，以较小步长更加细致地搜索。图3给出了初始值C=1，σ2=0.5时的寻优过程。

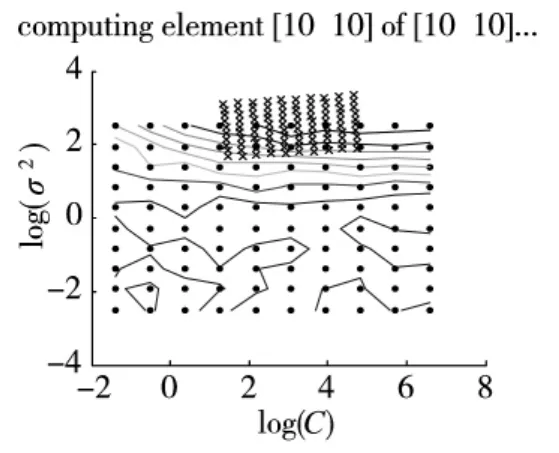
图3 初始值C=5，σ2=1的寻优过程

将得到的C与σ2最优值用于训练LS-SVM模型，进而完成对装备研制风险的综合评价。将编号11 和 12 的样本中的指标 E1，E3，E5，E6，E7，E10，E12值输入LS-SVM模型，并依据表5给出的风险综合评价等级取值范围，得到LS-SVM与RS-LS-SVM模型的评价结果对比如下页表6所示。

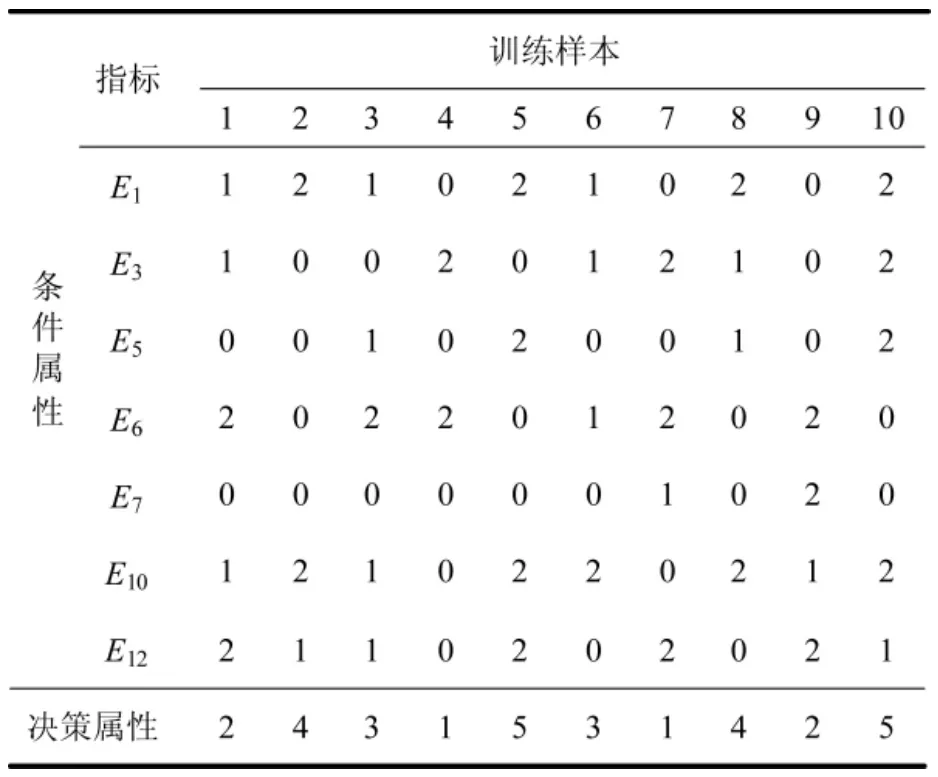
表4 最小约简后的决策表

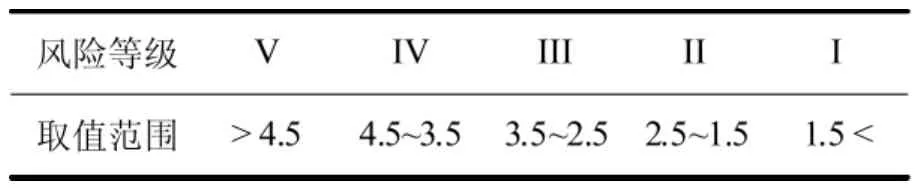
表5 装备研制风险综合评价等级取值范围

从装备研制风险评价结果可以看出，经过RS属性约简，原来12个属性中仅剩下7个，将这7个属性对应的样本训练LS-SVM模型，得到评价结果与SPA完全一致。这说明，RS不仅简化了LS-SVM网络结构，降低了运算复杂性，而且提高了预测精度，平均绝对误差（指所有单个观测值与算术平均值的偏差的绝对值平均）达到0.098，评价结果更接近SPA评价值。而单纯LS-SVM模型对编号12样本的评价结果却出现了偏差。因此，应用RS-LS-SVM进行装备研制风险综合评价是更为可行的。更重要的是，通过对装备研制风险评价体系中指标的分析与精炼，可极大地减少实际风险评价中信息收集与处理的工作量，使评价过程更为严谨、科学，评价结果也更为准确、有效。

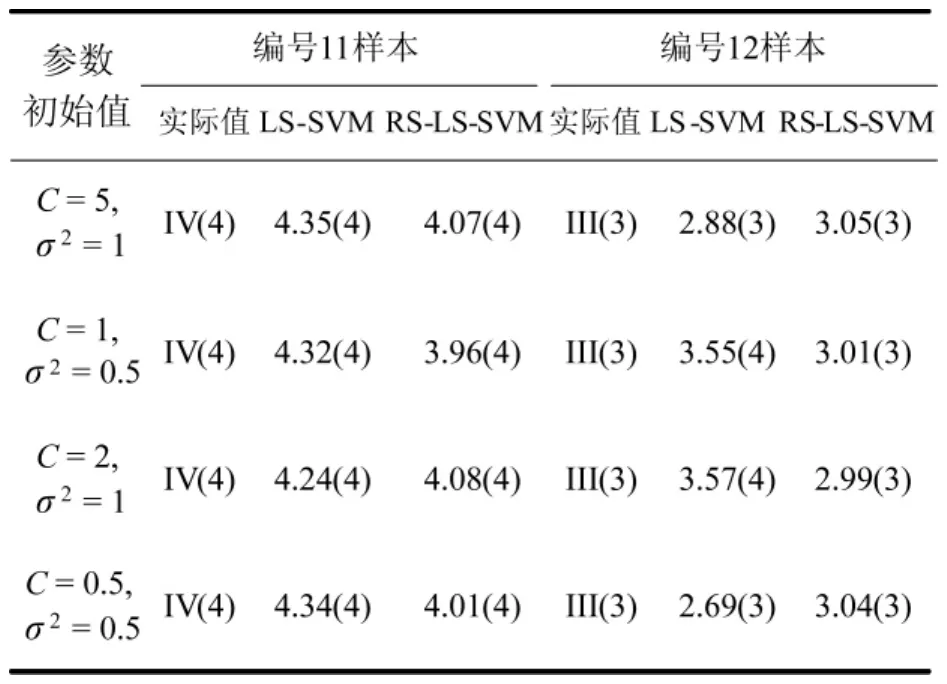
表6 LS-SVM与RS-LS-SVM模型评价结果对比

6 结论

本文先构建装备研制风险评价指标体系，引入SPA法生成训练样本和测试样本，将RS与LS-SVM进行优势互补，采用RS方法对装备研制风险LS-SVM评价模型的输入指标进行了属性约简，将12项输入减少到7项，并进行了相关测试与比较分析。数值分析结果表明，相对于单一LS-SVM评价模型，基于RS约简的LS-SVM模型既可以消除冗余信息，简化模型结构，又能够继承LS-SVM的自学习与联想记忆功能，给出更为准确、可信的评价结果。因此，采用RS-LS-SVM进行装备研制风险评价是可行的，同时，也为装备研制风险提供了一种有效的管控手段。