基于μ综合的PHEV模式切换协调控制*

李海晓，付主木，2*，李桢辉

（1.河南科技大学信息工程学院，河南 洛阳 471023；2.河南科技大学河南省机器人与智能系统重点实验室，河南 洛阳 471023）

0 引言

混合动力汽车（Hybrid Electric Vehicle，HEV）包含发动机和电机两种动力源，存在发动机、电机和混合3种驱动模式[1]。由于路况差异、负载变化以及一些其他外部干扰，需要在上述3种驱动模式之间切换[2-3]，以满足整车动力性和经济性需求。发动机和电机动态特性差异较大，离合器分离/结合过程复杂，切换过程中转矩波动较难避免，造成传动部件冲击较大，导致动力传递不平稳，影响到整车动力性和乘坐舒适性[4-6]。因此，需要对HEV模式切换过程进行协调控制。该方面的研究已引起了国内外学者的广泛关注，并取得了一些有意义的成果。

杜波[7]针对单电机重度HEV的模式切换，提出电机主动调速与离合器接合压力调控相结合的协调控制策略，提高了切换过程中动力传递的平稳性。倪成群等[8]采用发动机转速自适应闭环跟随电机转速的方法，研究了从纯电动模式到发动机或混合驱动模式的切换过程，使整车驾驶性有所改善。Zhu等[9]采用模糊增益比例积分微分控制器作为反馈来适应各种非线性，对HEV中动力传动核心部件进行动态建模与模拟验证，以降低模式切换转矩波动。Song等[10]针对一种PHEV，提出了一种电机控制算法，建立了评估模式切换性能的测试平台，验证了该控制方法的有效性。以上协调控制方法均在某种程度上实现了模式切换的平顺性，但某些方法对模型的要求较高，且未考虑HEV模型参数的不确定性[11-13]，降低了动态过程中的鲁棒性。

本文以PHEV为研究对象，对从纯电动模式切换到发动机驱动模式的动态协调控制问题展开研究。在分析混合动力系统动态切换过程及协调发动机和电机转矩的同时，考虑离合器和负载转矩变化对传动系统的影响，设计基于μ综合理论的鲁棒控制器，协调各动力源转矩的动态输出，并进行了仿真分析。

1 PHEV系统结构

PHEV系统结构如图1所示。主要由发动机、电机、电池等组成，发动机经离合器与电机相连且在同一轴线上。此外，发动机为主能源，电机为辅助能源，取长补短，兼具传统汽车和电动汽车的优点，以克服电动汽车续航里程短的缺点。

图1中，Te、Tm、Tc和 Tl分别为发动机输出转矩、电机输出转矩、离合器输出转矩和负载转矩；Je、Jc、Jm、Jw分别为发动机、离合器、电机和车轮转动惯量；we、wm、ww分别为发动机、电机和车轮转速；cw为车轮旋转黏性阻尼系数。

图1 PHEV系统结构图

2 模式切换过程分析

PHEV工作在纯电动模式时，若整车需求转矩大于纯电动最大转矩阈值或需求加速度大于纯电动能提供的最大加速度阈值，则系统发出切换至发动机驱动的命令，并将电机作为启动机。将纯电动驱动到发动机驱动的切换过程分为离合器结合前、后两部分。对前者，将切换指令发送给电机控制器，电机增加输出转矩，为整车驱动提供所需转矩，同时，将增加的额外转矩用于启动发动机，使发动机转速快速提高到怠速，并加速至与电机转速的同步，此时，离合器完全结合；对后者，由于发动机动态响应的滞后性，无法单独提供整车需求转矩，需要用电机对整车需求转矩进行补偿。为此，本文将该切换过程分为离合器滑摩Ⅰ、离合器滑摩Ⅱ、转速同步和转矩协调4个阶段。

1）离合器滑摩Ⅰ阶段（we=0）

本过程是指离合器传递的转矩小于发动机启动阻力矩阶段。离合器接收到整车控制器发出切换指令后，其压盘与摩擦片逐渐接触。此时，离合器开始为发动机传递动力，但并未带动发动机一起运转，其转速仍为0。该阶段传动系统模型为

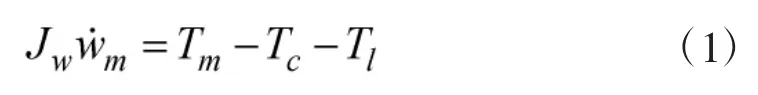
2）离合器滑摩Ⅱ阶段（we＞0）

本过程是指发动机转速由0提高至怠速阶段。当离合器所传递转矩增大到足以克服发动机启动阻力矩时，发动机开始随着离合器一起运转。该阶段传动系统模型为

其中，Ter为发动机启动阻力矩。

3）转速同步阶段

本过程是指发动机转速从怠速加速至与离合器输出端转速相同的阶段。此时，发动机已完成启动，发动机控制器将对其转速进行调节，直到。为降低整车冲击度，需降低离合器的结合速度。该阶段传动系统模型为

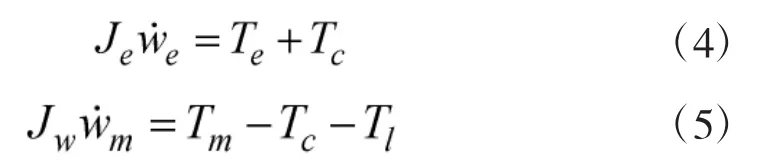
4）转矩协调阶段

本过程是指发动机与电机转速达到同步后至电机退出阶段。此时，发动机已完成调速，离合器快速结合。随着发动机输出转矩增加至需求转矩，电机转矩逐渐减小到0且退出工作。该阶段传动系统模型为

在离合器滑摩Ⅱ阶段和转速同步阶段，本文设计发动机鲁棒闭环控制以跟踪发动机速度参数，调节发动机从0至转速同步过程中的转速曲线；在转矩协调阶段，设计电机鲁棒闭环控制，用电机补偿发动机需求和实际转矩的差值及传动系统的干扰，直至发动机转矩达到目标转矩，电机退出工作。

3 基于μ综合的模式切换鲁棒控制器设计

对于存在结构化不确定性的系统，用结构奇异值方法进行控制器设计的过程叫作μ综合[14]，较适用于处理具有参数不确定性系统的鲁棒控制器设计。其原理为将被控对象、外部干扰等产生的不确定性统一成一个闭环回路，把实际控制系统设计转化为结构奇异值[15]，对参数变化、模型误差和外来干扰等不确定性具有较好的鲁棒性。

PHEV模式切换过程中，综合考虑系统内发动机、电机转速测量误差以及系统外道路和负载变化等状况，设计基于μ综合的模式切换鲁棒控制器，以提高传动系统的鲁棒性，降低切换引起的整车冲击度。

3.1 μ综合鲁棒控制结构

本文依据PHEV系统结构、发动机和电机模型存在的不确定性，对模式切换过程设计鲁棒控制闭环回路，实现对发动机与电机输出转矩和转速的协调控制。

在离合器滑摩Ⅱ和转速同步阶段，发动机侧转速跟踪鲁棒控制器如图2所示。整车需求转速经发动机控制器Ke后，将信号传递至发动机，发动机启动，经闭环系统实现发动机实际转速对需求转速的跟踪。

图2 发动机侧转速跟踪鲁棒控制器

图2中，虚线部分是发动机实际模型，用PE表示，包括发动机模型误差ΔGe、乘法不确定性的加权函数We、发动机执行器Ae和发动机的转矩动态响应，即。ωe_cmd为发动机的需求转速，Ke为基于发动机不确定性设计的μ综合控制器，ue为发动机输入转矩，z1为发动机输出转矩角速度的误差，z2为发动机反馈控制结果，wTcd为离合器转矩估计误差，we_dis为发动机转速测量噪声。

在转矩协调阶段，电机侧转矩补偿控制器如图3所示。综合考虑离合器分离/结合状态、负载变化情况等对传动系统的影响，利用电机转矩快速补偿发动机需求转矩与实际转矩间的差值，以满足整车转矩需求。

图3 电机侧转矩补偿控制器

图3中，虚线部分代表实际电机模型，用PM表示，包括电机模型误差ΔGm、乘法不确定性的加权函数 Wm、执行器Am和电机的转矩动态 Pm（s），即。Tm_cmd为电机的需求转矩，Km为基于电机不确定性设计的μ综合控制器，um为电机输入转矩，z3为电机输出转矩角速度的误差，z4为电机输出转矩角速度，z5为电机反馈控制结果，wTld为负载转矩干扰，wm_dis为电机转速测量噪声。

对于μ综合鲁棒控制器的设计，加权函数的选择至关重要。图2和图3中，输入加权函数Wcmd和Wcmd2一般应使发动机和电机的输入参数与实际输入信号接近，因此，选择低通高衰滤波器：，wemax和wmmax分别为发动机、电机最大转速；测量噪声输入权值函数，，其频率较高；加权函数，分别为对发动机、电机控制信号幅值的约束，uemax和ummax分别是发动机、电机的最大反馈控制信号；频率加权函数Wperf1、Wperf2和Wperf3是为了保证发动机、电机速度跟踪误差及角速度输出而设计的性能指标。

为此，将模式切换中发动机和电机的鲁棒控制问题转化为控制器Ke和Km的求解问题。在Ke、Km的共同作用下，使发动机和电机的转矩和转速平稳变化，以减小模式切换过程的冲击，达到平滑切换和提高系统的鲁棒性的目的。

3.2 鲁棒控制器求解

为了确定控制器Ke和Km及加权函数参数，将与各个权函数合写成广义对象的形式，将图2和图3用线性分式变换表示如图4所示。

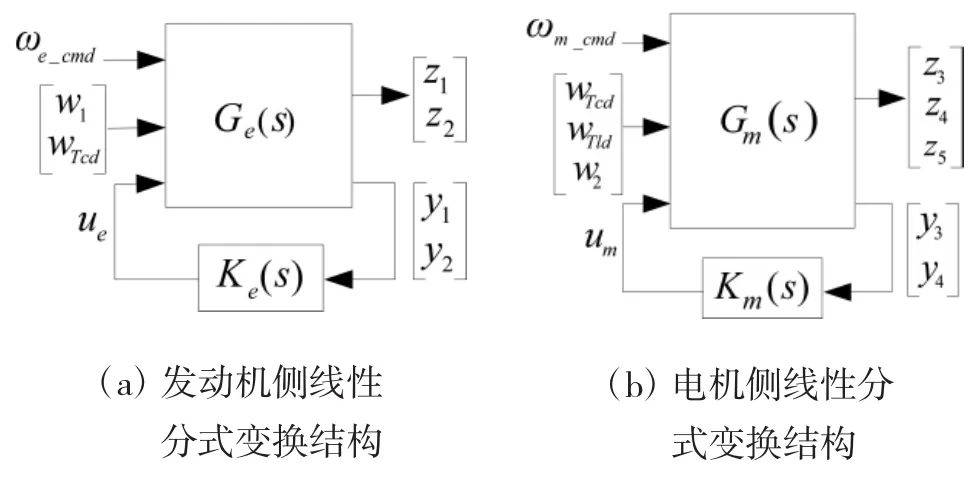
图4 鲁棒控制器的线性分式变换结构

为此，将μ综合问题转化为控制器K的求解问题，且满足如下不等式约束条件

采用D-K迭代法可求解此类问题，结构奇异值μ通过其上界来近似求解，且利用定标阵D（ω）获取，即

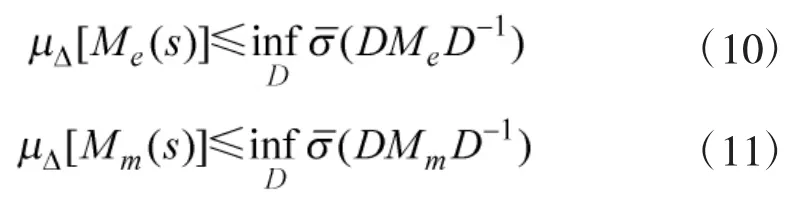
得出下列的优化问题

由此，可将该优化问题化为二参数的极小化问题，即

对于发动机控制部分，可按照如下步骤进行：

第2步，在第1步基础上，求取ωe下对应的，使最小；

具体迭代结果如表1所示。

表1 发动机侧控制器迭代结果

由表1可以看出，经3次迭代后，可得到30阶控制器，μ的峰值为0.966，较接近理想值，满足系统鲁棒性要求。但由于阶次过高，本文利用Matlab/Simulink工具箱，采用截断的均衡模型将控制器降为5阶，保持了原系统的鲁棒性，简化了计算量，简化后的发动机控制器Ke为

采用类似方法，可得到电机控制部分的迭代结果如表2所示。

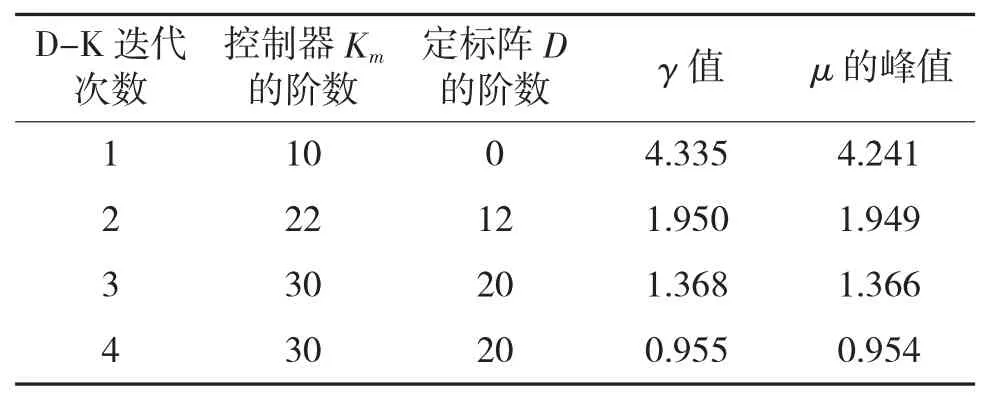
表2 电机侧控制器迭代结果

经降阶简化后，电机控制器Km为：

4 仿真和对比分析

为了对本文所设计的控制策略进行验证，在Matlab平台上，搭建了PHEV系统及核心传动部件仿真模型。动力传动系统主要核心部件参数如表3所示。

表3 动力传动系统主要核心部件参数

将PHEV动力学方程和控制算法嵌入到Matlab/Simulink中，对由纯电动切换至发动机驱动过程进行动态仿真，结果如图5～图7所示。PHEV运行10 s后，整车控制器发出切换信号，车辆进入离合器滑摩Ⅰ阶段，此时，发动机开始克服其启动阻力矩，其转矩仍为0；当车辆运行到10.2 s时，进入离合器滑摩Ⅱ阶段，此时，发动机转速由0增至怠速，电机转矩和转速随整车需求转矩和转速的增大而迅速上升；当车辆运行到10.5 s时，进入转速同步阶段，此时，发动机转速趋于电机转速，离合器完全结合；当车辆运行至10.9 s时，进入扭矩协调阶段，此时，电机对发动机进行转矩补偿，满足整车需求转矩，发动机转矩平稳上升。

图5 发动机和电机的需求和实际转矩

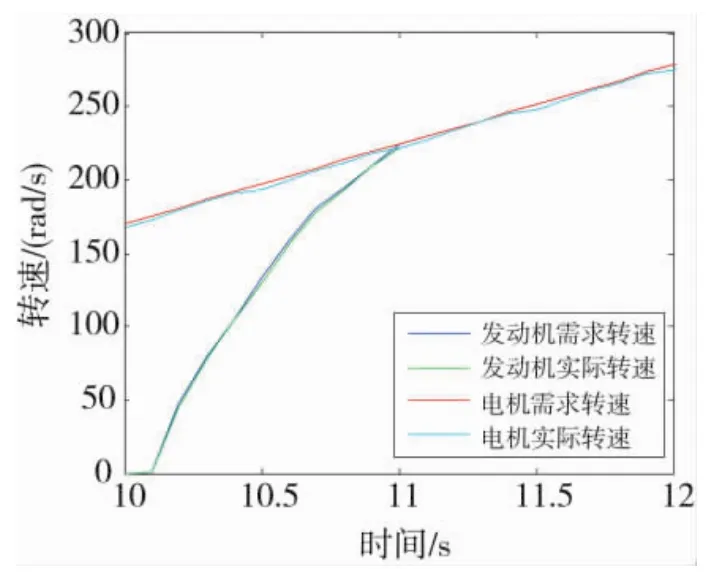
图6 发动机和电机的需求和实际转速

图7 整车纵向冲击度

由图5和图6可知，在整个切换过程中，发动机、电机输出转矩、转速均能较好地跟随整车需求转矩、转速，且它们的模型和转速测量等误差对切换过程几乎没有影响。在模式切换时，发动机转矩逐渐增至满足整车需求转矩；电机与发动机达到转速同步后，电机转矩并未立刻降为0，而是根据发动机输出转矩和目标转矩要求，对整车需求转矩进行补偿，提高了动力传递的平稳性。在10.5 s时，发动机转速由0上升至怠速，在上升过程结束，且发动机和电机转速同步后，离合器快速结合；发动机开始整车运转，此时，电机转矩逐渐减小为0，完成整个模式切换过程。

由图7可知，采用本文所设计的控制器，冲击度降为7 m/s3，小于我国冲击度限制推荐值17.64 m/s3，提高了动力传递的平顺性。

5 结论

1）建立PHEV动力系统从纯电动切换至发动机驱动过程的动力学模型，对纯电动切换至发动机驱动过程进行动力学及干扰等不确定性分析，并将该过程划分为4个阶段，简化了控制复杂度。

2）采用μ综合控制理论，利用发动机转速跟踪和电机转矩补偿的方法，分别设计了发动机和电机鲁棒控制系统，对控制器Ke、Km和加权函数参数进行了求解，降低了切换过程中总需求转矩的波动和整车冲击度，实现了PHEV的切换平顺性。

3）仿真结果表明，所设计的基于μ综合的鲁棒控制，整车冲击度绝对值的最大值为7 m/s3，降低比率为60.3%，减小了外部干扰和模型不确定性对系统性能的影响，降低了模式切换所引起的转矩波动。

在本文设计过程中，将离合器转矩视为传动系统干扰量，如何精确控制离合器接合轨迹，将作为下一步的研究重点。