一种组网探测资源管控拓扑模型优选算法*

段艳红，丁建江，赵志强

（1.空军预警学院，武汉 430019；2.空军装备部，北京 100034；3.解放军95333部队，长沙 410114）

0 引言

目前，空天目标种类多样性、特征复杂性、突袭方式灵活性、威胁严重性，催生了预警探测装备向体系级不断发展。雷达组网系统[1]作为体系探测装备中的一种，具有有形（如雷达）和无形（如频率协同）的探测资源以及基于网络体系结构[2]的资源管控优势，如何设计有效的管控拓扑模型优选算法，实现对探测资源的高效管控是当前待解的难题。从目前国内外公开的研究成果来看（或许由于保密原因），关于探测资源管控拓扑模型如何优选多是凭经验主观判断，缺乏客观和科学的选择依据，并且与之相关的学术成果[3-5]多是定性角度进行研究，缺少具体的量化分析。Mahendra等[6]从任务调度与分配的角度，系统总结了资源管控的基本问题和方法，知识涵盖了多个领域；而借鉴复杂网络的计算方法用于解决武器装备体系应用的问题出现在了Guariniello等[7]的研究成果中，具有一定的科学性和启发性；Iliev等[8]讨论了无线传感器网节点的覆盖控制问题，涉及了多种节点定位方法，为节点控制问题提供了新的研究途径。上述研究跨越了多个学科的多种领域，能够从某一方法的角度较好地解决相关的问题，但是针对探测资源管控拓扑模型优选难题，传统的经验主观选择方法已难以满足雷达组网系统决策者对科学性和客观性的需要。因此，本文试图通过研究探测资源管控拓扑模型特点，利用图论[9]和社会网络分析[10]的方法对探测资源管控特性进行形式化表示，建立了管控信息流图论模型和优选算法流程，提出了探测资源管控拓扑模型优选的新算法，与主观选择法相比，更具有客观和可操作性，适用于拓扑模型优选。借助优选示例进行了仿真计算，得出具有参考价值的结论，为雷达组网系统决策者提供重要的借鉴。

1 算法理论基础

1.1 探测资源管控节点的结构特征

美国A2C2（Adaptive Architectures for Command and Control）[11]项目的核心技术之一就是团队集成设计环境（Team Integrate Design Environment，TIDE）。它将组织结构理论和系统工程方法有效地融入到了团队设计环境中。合弄制造系统（Holon Manufacturing System，HMS）中的Holon技术优势是：Holon体之间的协作以及对自身内部资源的有效管理[12]。将TIDE与Holon相结合构建的团队合弄集成设计环境（Team Holon Integrate Design Environment，THIDE），可以综合TIDE的团队优化配置成果和Holon技术的优势。图1给出了基于THIDE的探测资源管控节点内部结构，该管控节点既可以是受控雷达，也可以是嵌入到雷达中的功能模块或者平台。通过团队目标到管控任务的分析，并对多变量参数约束的目标函数进行求解，得到优化的结构解，进行团队的优化配置，再与Holon技术优势的交互，使得管控效率得到提升。

图1 基于THIDE的探测资源管控节点内部结构

1.2 基于THIDE和图论的探测资源管控拓扑模型

面对复杂多变的信息对抗环境，需要构建多样化、实用性较强和可选择的基于网络体系结构的探测资源管控拓扑模型。图2给出了基于THIDE和图论的雷达组网探测资源管控信息流程示意图，其中实线箭头为探测资源管控指令信息流，虚线箭头为探测资源管控指令反馈信息流。

图2 基于THIDE和图论的探测资源管控拓扑模型示例图

2 算法模型

2.1 算法流程

优选算法中引入模糊物元[13]分析法，它是对管控拓扑模型优选量化模型中不确定特征定量分析的一种独特数学工具，并对其进行改进，以此解决管控活动中信息的可变性，算法流程如图3所示。

图3 基于改进模糊物元的拓扑模型优选算法流程图

2.2 节点特性指标量化模型

通过图论可知，探测资源管控拓扑网络是由管控THIDE节点集J和边集B组成的图G=（J，B），为了方便讨论，本文的管控THIDE节点是指嵌入了THIDE功能模块的单部雷达，不具体区分各管控THIDE节点的个体差异，且不考虑自环的情况。借鉴社会网络分析方法[10]，指标含义及量化模型如下：

2.2.1 探测资源管控信息可用度T1

其含义是表示在某个管控活动中，雷达i对管控信息的利用和反馈程度。借鉴网络流通度量方法[14]，其计算模型为：

其中，R（i）为雷达 i的聚焦系数[15]。

2.2.2 探测资源协同贡献度T2

探测资源协同贡献度是度量管控拓扑网络中雷达i为达到协同探测效果通过各种关系与其他雷达节点协同探测的贡献量。记雷达i的探测资源协同贡献度为，其计算公式为：

其中，n为管控网络的雷达总数。lij为雷达i到j的管控捷径，这里用捷径矩阵中的元素作为其度量值。bij为雷达i与j构成的相互关系，用邻接矩阵[16]中的元素作为其度量值。

2.2.3 探测威力信息贡献度T3

雷达探测威力贡献度就是赋予每部雷达一定的探测威力信息“核心度”，可理解为两部雷达协同探测过程中交换的探测威力信息是关于二者与管控信息核心的接近性程度。在本文中采用连续核心边缘分析模型[17]。

确定核心度∂i的模型为：

其中，P为皮尔森相关系数，αij表示的是雷达i和j的协同探测关系是否存在，存在取值为1，否则为0，n为雷达总数。

2.2.4 探测资源管控关系强度T4

探测资源管控关系强度是度量雷达i在充当中介角色的可能。考虑管控信息的复杂性，故其计算模型为：

2.2.5 信息中心度T5

其含义是表示在某个管控活动中将该受控雷达i置于休眠状态时引起的雪崩效应[19]，记为，其表达式如下：

其中，E（g）和 E（G）的含义及量化见文献[20]。

2.2.6 特征向量中心度T6

进行特征向量中心度[21]研究是为了找到最有力量倍增效果的雷达，量化分析如下：

令A为邻接矩阵，其元素aij的含义是雷达i对j的信息互补效果，令中心度值向量为：

那么特征向量中心性模型可表达为：

其中，xi为雷达i所对应的特征向量的分量。

2.2.7 探测资源管控优势T7

探测资源管控优势是衡量雷达i的探测信息影响范围大小的指标，度数中心度[22]越高者，表示其在管控网络中与较多的组网雷达节点构成信息相互印证的关系，其表达式如下：

其中，d（i）为雷达 i的度数[23]，n 为雷达总数。雷达 i的探测资源管控优势采用相对度数中心度模型进行度量，计算公式如下：

2.2.8 探测信息集成度T8

“相邻”是对两部雷达节点协同控制的图论表达，点i的邻点个数称为该点的度数，也叫关联度[23]，表示对管控网络中所有“邻点”雷达的管控信息融合程度，即为雷达i的探测信息集成度指标，记作d（i），其计算模型为：

其中，ni为雷达i的邻点个数。

由以上各指标含义分析可知，除信息中心度指标为极小值极性外，其余指标均为极大值极性。本文所提指标可针对具体应用的需要适当地进行调整和扩充。

2.3 管控势能模型

雷达组网探测资源管控势能是指在特定的管控拓扑模型中，每部雷达按照体系探测任务，利用信息进行协同管控，以融合为该拓扑模型的整体管控优势。信息是信息论[24]中的核心，同时也是雷达组网系统工作的驱动力；为了消除管控活动中存在的大量随机性和不确定性，使信息优势转化为管控优势，建立信息论和模糊物元分析法相结合的优选算法是合理的，这也是本文算法设计的依据。

2.3.1 管控信息熵模型的建立

设管控拓扑模型中相互独立的状态变量向量为：

其相应的概率向量为：

由于每一状态ti的概率不尽相同，所以自信息量也不相同，以此来计算该管控拓扑模型中各雷达节点管控信息具有不确定性数量的数学期望，记为，表达式如下：

2.3.2 管控信息熵模糊物元的定义

在管控拓扑网络中所描述的雷达节点G及其特征T和量值Z组成物元F=（G，T，Z），如果物元模型中的量值Z具有模糊性，便称其为模糊物元。如果模糊物元中节点的特征为管控信息熵，则称为管控信息熵模糊物元。若管控信息熵模糊物元中有m个节点，则为m个节点的复合信息熵模糊物元。

2.3.3 各类物元的构造

m个节点的n维物元组合在一起便构成m个节点的n维复合物元R，记为：

其中，Gj为第个节点；Ti为第个特征；zij为第j个节点的第i个特征量值。

为了更充分地反映各指标的极性和相对性，采用如下形式计算各指标模糊从优隶属度：

1）极大值极性指标：

2）极小值极性指标：

其中，ξij为从优隶属度；分别为同一指标下各特征量值中的最大值和最小值。由此可以构建从优隶属度模糊物元Q：

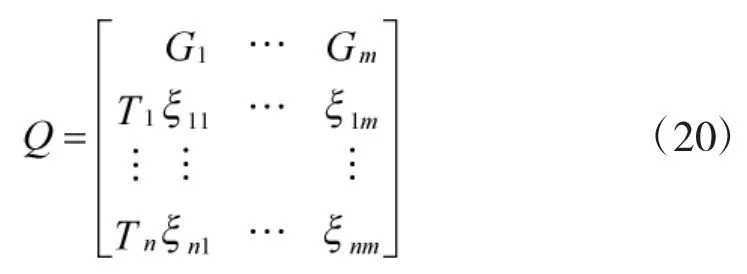
2.3.4 指标权重的确定

在指标赋权时，多采用层次分析法[25]的主观定权法，但易造成主观因素的偏差。为了消除这种偏差，使优选结果更符合实际，可选用满足客观性要求的熵权法[26]，其计算步骤如下：

1）将R作为判断矩阵。

2）将判断矩阵中的量值zij作如下归一化处理：

其中，ηij为归一化量值；分别为同一指标下各雷达节点量值中的最大值和最小值。

3）根据熵的定义，m部雷达的n个指标，可以确定第i个指标的熵为：

为使 lnσij有意义，需定义σij为：

其中，第i个指标的熵权为：

2.3.5 复合模糊物元的构造

由上述计算模型便可构造优选时第j个节点的概率复合模糊物元和自信息量复合模糊物元，分别用Fj和Yj表示，则有：

其中，

2.3.6 管控势能模型的建立

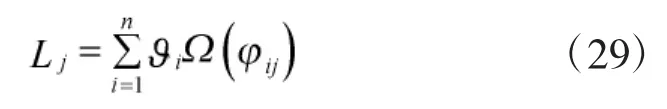
设管控势能中含有的不确定性加权自信息总量为Ic，该管控拓扑模型的管控势能为Ec，且Ec的值介于0和1之间；则管控势能中含有的不确定性即为整个管控拓扑模型带来的不确定性加权自信息总量，即：

所以管控拓扑模型的管控势能为：

其中，wj为第j个雷达节点的权重。

3 算法验证

现用3种管控拓扑模型（1、2和3）的示例对本文优选算法进行验证。依据上级赋予的3个阶段（A、B和C）体系抗干扰任务，对分别嵌入THIDE功能模块的7部可机动雷达（对应为THIDE1，THIDE2，…，THIDE7）进行分布式组网，雷达组网系统决策者预先构建了3个阶段相应的探测资源管控拓扑模型。阶段A、B和C分别对应拓扑模型1、2和3。通过考核各阶段对应拓扑模型管控势能的大小来进行动态适时决策。为便于理解和计算，建立了各拓扑模型的图论模型，如下页图4所示。

现结合示例和2.2节，对以上各拓扑模型的节点特性指标进行具体量化。由图4图论模型，并借助MATLAB和UCINET仿真软件求得各拓扑模型的节点指标量化矩阵如表1所示，量化值客观地反映了3种拓扑模型中各THIDE节点的不同特性指标值的大小，为模型优选的下一步计算提供科学和可靠的数据支持。

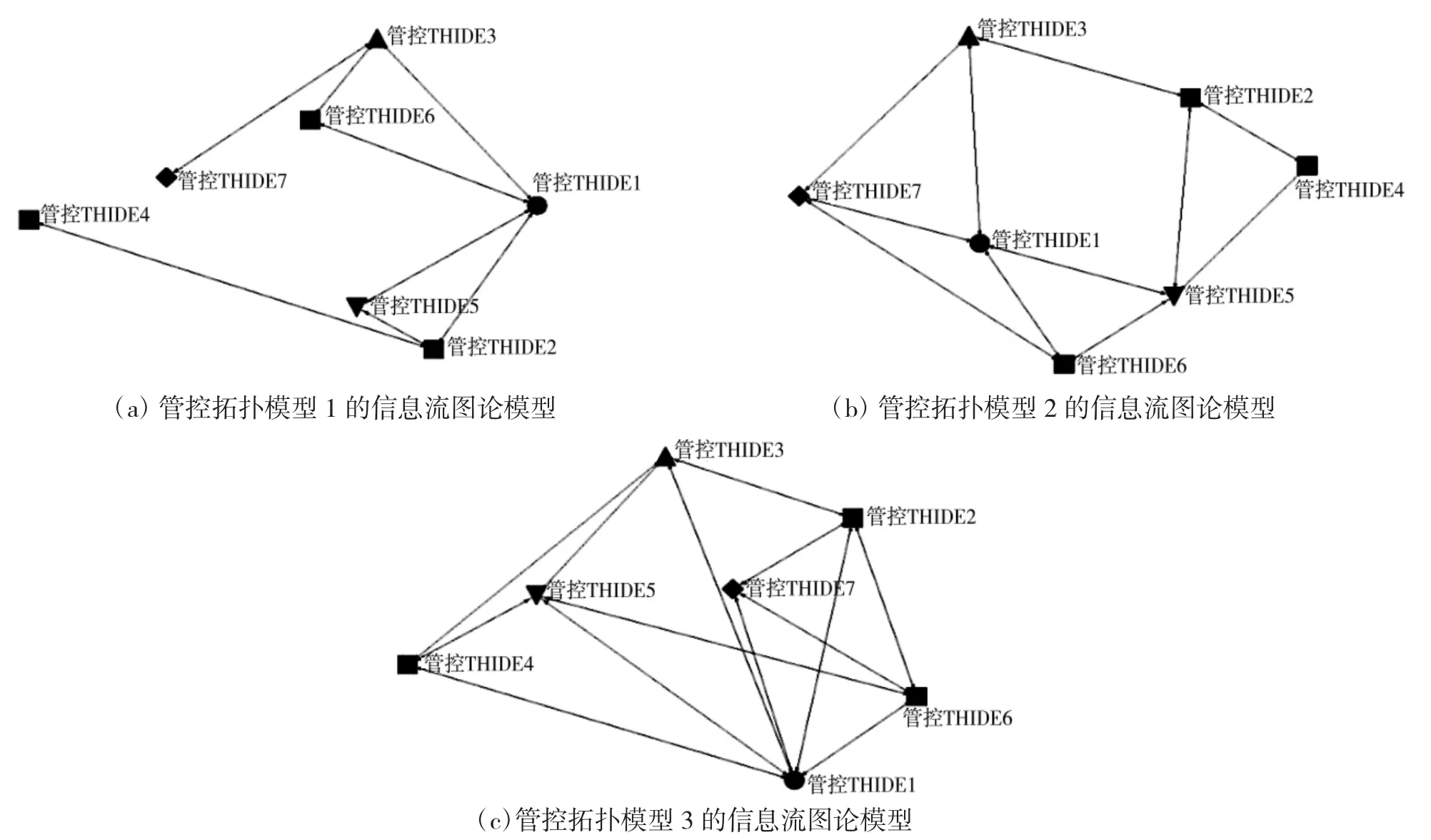
图4 3种管控拓扑模型的信息流图论模型

在求得管控拓扑模型中的各个节点诸指标特性值的基础上，结合指标极性的特点，通过MATLAB仿真计算，得出3种拓扑模型中管控THIDE节点相应的不确定性加权自信息总量并加以对比，如下页图5所示。由图5可见，拓扑模型3的不确定性加权自信息总量曲线相对其他两种模型的较平缓，拓扑模型1的则起伏较大；随着网络由拓扑模型1动态变化到3，节点4的不确定性加权自信息总量逐步减少。仿真表明：由于网络动态变化中各THIDE节点之间连接关系的增加，使得节点间通过信息的沟通来合理平衡网络中各节点之间不确定性加权自信息总量，达成协同管控的效果。

图5 3种管控拓扑模型中各节点的不确定信息量

结合2.3.6中管控势能计算模型，经仿真计算得出3种管控拓扑模型的加权不确定信息总量和最终的管控势能比较结果（如表2）。由表2可见，随着网络由拓扑模型1动态变化到3，各节点之间的连接关系增加，使得网络整体的加权不确定信息总量逐步减少；随着任务的进行，各节点之间横向和纵向的联系增加，生成了基于网络体系结构的管控能力，促使拓扑模型的管控势能增加，将管控势能的高低作为拓扑模型优劣选择的依据，由表2可以得出拓扑模型3是优选的结果，这与实际情况也是相吻合的；因此，本文优选算法是合理的。

表2 3种拓扑模型的管控势能仿真结果对比

为了验证本文算法的有效性，用文献[27-28]的算法分别对上述示例进行求解，并将所得的拓扑模型优选量值与本文算法结果进行对比，如图6所示。3种算法的优选量值高低依次是拓扑模型3、2和1，虽然3种算法衡量的角度差异导致了值的大小差异，但是各算法优选排序结果是一致的；因此，本文算法的有效性得以验证。综合表2的结果分析，说明本文算法是可行的。

图6 3种算法仿真结果对比

4 结论

本文提出的优选新算法，将图论、社会网络分析法、信息论与物元分析方法有机结合，通过阶段变化时网络结构的动态拓扑模型示例，对算法的有效性进行了验证。研究与仿真表明，雷达组网系统决策者通过在管控拓扑模型中建立管控THIDE节点之间较多的横向和纵向关系，来达成基于网络体系结构的显著特征，能够提高该拓扑模型的管控势能，继而将管控势能转化为管控优势，为雷达组网探测效能的提升提供优选的管控拓扑模型。算法适用于进行组网探测资源管控拓扑模型优选和网络动态变化时的发展规律量化分析，可解决雷达组网探测资源管控拓扑模型优选的问题。然而，拓扑模型优选指标在其他具体应用中如何合理调整，还需要进一步研究。