非对称轴向柱塞泵斜盘力矩特性研究

， ， ， ，

(1. 北京航空航天大学机械工程及自动化学院， 北京 100191；2. 北京精密机电控制设备研究所， 北京 100076)

引言

非对称柱塞泵以其良好的预升压及高压化能力被广泛地应用于航空航天领域。在柱塞泵的实际工作过程中，斜盘受高频、交变力矩作用，对泵的寿命、噪声及变量特性均有重要影响，是制约轴向柱塞泵向高压、大功率、快响应方向发展的因素之一[1-2]。斜盘承受力矩通过实验手段较难测量，如何通过数学计算和仿真手段对斜盘承受力矩进行理论计算和仿真对变量机构的设计，伺服电机的选型有着重要的指导意义[3]。

本研究以某航空航天用变量柱塞泵展为研究对象，利用MATLAB进行斜盘力矩的数值计算，并在AMESim环境下建立柱塞泵的仿真模型，搭建了柱塞泵斜盘力矩测试仿真实验台，进行斜盘力矩仿真对比实验。

1 非对称配流结构斜盘力矩数学模型

对非对称配流柱塞泵斜盘进行受力分析，如图1所示。斜盘主要承受柱塞对斜盘的液压力Fb、柱塞摩擦力Ffs、柱塞惯性力Fg、滑靴摩擦力Ffp等。

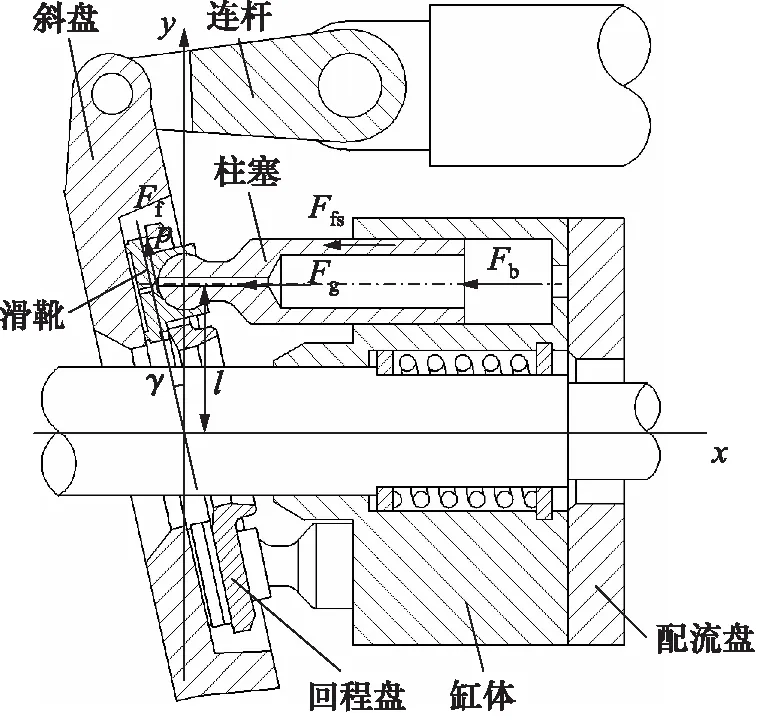
图1 柱塞泵斜盘受力简图

斜盘承受的力矩Ms主要包括柱塞对斜盘的液压力矩Mb、柱塞摩擦力矩Mfs、柱塞惯性力矩Mg、滑靴摩擦力矩Mfp，即：

Ms=Mb+Mfs+Mg+Mfp

为了准确得到斜盘承受的力矩，分别对斜盘承受的液压力矩、惯性力矩和摩擦力矩的数学模型进行求解。

1.1 液压力矩

单柱塞在任意角度的液压力矩为：

(1)

式中，pi—— 第i个柱塞腔内的压力

dz—— 柱塞直径

df—— 柱塞分布圆直径

γ—— 斜盘倾角

φ—— 主轴转角

Z—— 柱塞数

柱塞腔体内部压力的大小与泵的配流盘机构有关，为了求得其压力的变化规律，需要对柱塞泵的配流进行分析。进而建立柱塞腔压力的数学方程及斜盘承受液压力矩的数学模型。

该高压柱塞泵配流盘与柱塞缸体腰型通油窗口的结构如图2所示。

为了提高泵的预升压，该柱塞泵具有较大死区，通过计算可知， 在泵旋转过程中至少有一个柱塞位于死

图2 配流盘及腰型窗口结构示意

区。因此对于该泵，传统液压力矩的计算公式[4]不再适用，采用数学分析的方法对液压力矩计算。为了简化计算，做出如下假设：

(1) 柱塞通油口与配流窗口联通时，忽略建立压力所需要的时间，即柱塞内的压力瞬间达到配流窗口压力；

(2) 将配流窗口等效为一理想恒压源。

基于以上假设，可以求得柱塞在转过不同角度时，柱塞腔压力的数学方程为：

式中，p0—— 柱塞位于上死点时柱塞腔的压力

pc—— 泵出口压力

pr—— 泵入口压力

p3—— 柱塞位于下死点时柱塞腔的压力

Vd—— 柱塞无效容积

1.2 柱塞摩擦力矩

任意φ角下单个柱塞与柱塞腔壁之间的摩擦力为pfs，则一个柱塞的摩擦力矩为：

(2)

全部柱塞的摩擦力矩的平均值为：

(3)

由公式可知，柱塞的摩擦力矩与柱塞腔压力无关，即与柱塞泵配流无关。

1.3 柱塞惯性力矩

任意角φ下，单个柱塞的惯性力矩为：

(4)

全部柱塞的惯性力矩的平均值为：

1.4 滑靴摩擦力矩

滑靴摩擦力矩的计算公式：

(6)

式中，Fz—— 柱塞底部面积

f—— 球铰摩擦系数

r—— 柱塞球头半径

1.5 非对称配流与对称配流斜盘力矩对比

由式(1)～式(6)知，斜盘承受的液压力矩与配流有关，而柱塞的惯性力矩、摩擦力矩、滑靴的摩擦力矩与配流无关。只需要对斜盘承受的液压力矩进行对比。对于非对称配流斜盘承受的液压力矩，利用1.1中公式，斜盘倾角取18°。通过MATLAB进行数值计算，单柱塞在单个周期内对斜盘液压力矩大小如图3所示。

将全部柱塞按照360°/Z的相位差进行叠加，得到全部柱塞对斜盘的液压力矩在一个周期内的变化如图4所示。

而对于对称小死区配流斜盘承受液压力矩，由于柱塞腔体内压力大小关于斜盘转轴对称，此时全部柱塞对斜盘转轴的液压合力矩为0[4]。显然，对于非对称配流，尤其是含有大死区的非对称配流，柱塞的液压力矩不可忽略。

图3 单个柱塞对斜盘液压力矩Mbs大小(γ=18°)

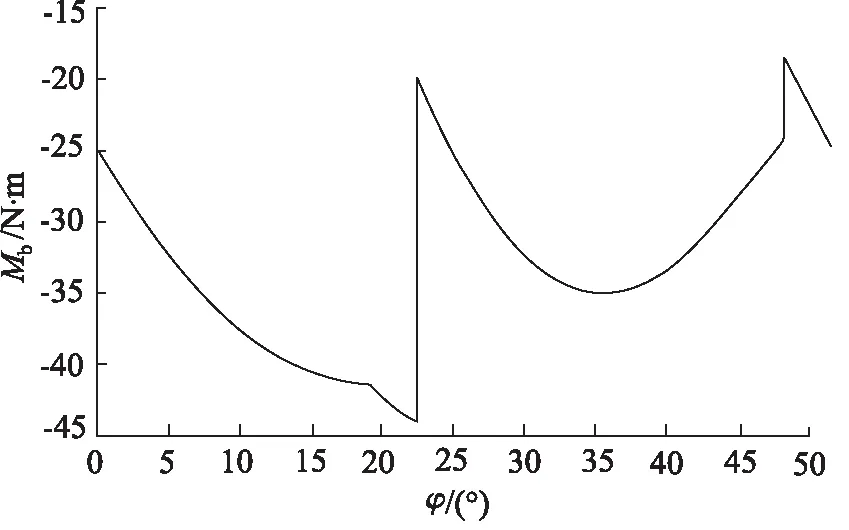
图4 斜盘承受液压力矩Mb大小(γ=18°)

2 柱塞泵AMESim物理模型建立

2.1 单柱塞物理模型建立

在AMESim中搭建单柱塞物理模型如图5所示，柱塞的摩擦和行程等参数用带限位摩擦的质量块模型来进行建模。将柱塞运动分为由于斜盘倾角改变引起的柱塞运动及由于主轴带动缸体转动引起的柱塞运动两部分，分别通过函数1和函数2进行数学描述。柱塞与缸体间的缝隙由环形阻尼口的液压组件模型进行建模。柱塞蹦的配流曲线通过查表的方式进行仿真，通过载入不同配流参数表， 可以简单、快速、高效地对比对称与非对称配流斜盘承受力矩大小。柱塞的相位差通过柱塞序号进行补偿。

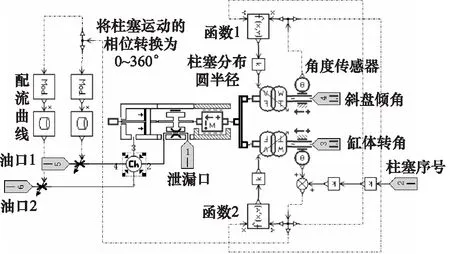
图5 单个柱塞AMESim模型

将柱塞腔同与其相应的配流模型封装为超级元件，如图6所示。

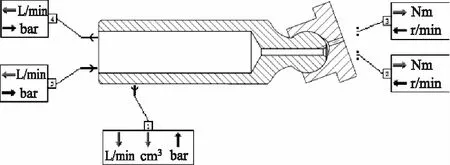
图6 柱塞超级元件

2.2 柱塞泵模型

将7个柱塞按照相位差为2π/7依次排开，将7个柱塞的速度与力矩进行求和运算，通过输入斜盘转角的角速度及主轴转速，可以模拟仿真出斜盘和主轴承受的力矩大小。

将柱塞各接口与斜盘、主轴连接，连接好各柱塞之间的油路，可以得到柱塞泵的AMESim模型，将该模型进行封装，建立变量柱塞泵的超级元件，如图7所示。

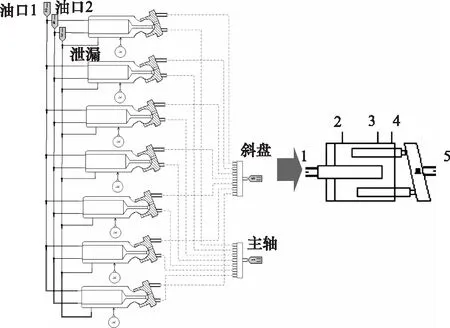
图7 变量柱塞泵AMESim模型

2.3 斜盘承受液压力矩测试模型

为了验证斜盘承受的液压力矩的变化规律，建立如图8所示的液压系统，利用2个溢流阀来建立系统工作压力，利用增压油箱来给系统补油，该系统结构简单，验证效果明显，采用溢流阀代替液压缸及负载，建立压力方便快捷。

3 仿真分析

3.1 非对称配流单柱塞液压力矩大小

为了更好地与数学模型进行比较，设置仿真系统的主要参数如下：增压油箱调整系统背压为0.5 MPa，溢流阀设置系统压力为28 MPa，斜盘倾角为18°，柱塞泵主轴转速为7000 r/min。仿真时间1 s，采样间隔0.0001 s，在AMESim平台进行仿真分析，单柱塞对斜盘产生力矩大小仿真曲线与系统压力仿真曲线如图9所示。

图8 斜盘承受力矩分析仿真系统

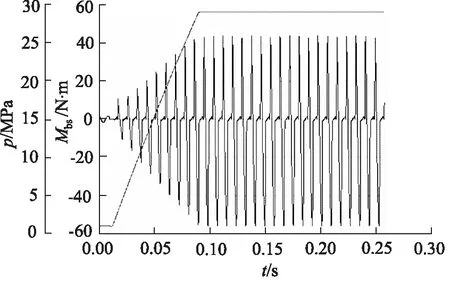
图9 单柱塞对斜盘力矩Mbs大小(γ=18°)

由仿真曲线可知，随着系统压力的提升，斜盘承受的液压力矩逐渐增大，当压力达到工作压力时，单柱塞对斜盘的液压力矩呈周期性变化。

当压力稳定时，取一个周期内单柱塞对斜盘液压力矩变化的图像，与数学模型进行对比分析，如图10所示。由此可以看出单个柱塞对斜盘的力矩有很大的脉动，其仿真模型与数学模型基本吻合。由于数学模型没有考虑建立压力的过程及泄漏对预升压的影响，故仿真模型与数学模型有一定偏差。

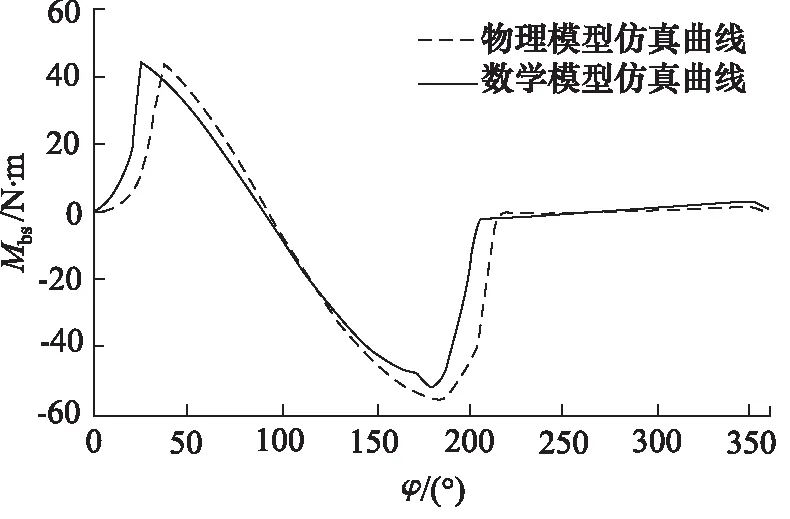
图10 数学模型与物理模型斜盘液压力矩大Mbs小比较

3.2 非对称与对称配流液压力矩大小比较

通过改变柱塞配流参数，研究非对称配流与对称配流液压力矩的变化规律。非对称配流压油窗口配流曲线如图11a所示，对称配流如图11b所示。

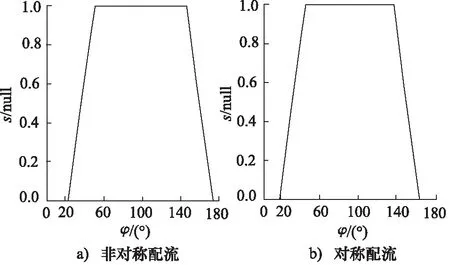
图11 非对称配流与对称配流曲线

仿真系统的主要参数为：增压油箱压力0.5 MPa；系统压力28 MPa，斜盘倾角18°(0.02 s从0°调整为18°)，主轴转速7000 r/min，仿真时间0.2 s，采样间隔0.0001 s。

分别对2种配流方式斜盘承受液压力矩进行仿真，其结果如图12所示。采用对称配流时液压力矩在0点附近快速变换，液压力矩的平均值约为0， 可以忽略不计，而当采用非对称配流时，液压力矩均值约为40 N·m，为斜盘主要承受力矩，不可忽略。

图12 非对称与对称配流斜盘承受液压力矩Mb仿真结果

3.3 斜盘倾角对液压力矩的影响

由3.1的仿真结果可知，系统压力对斜盘力矩的大小起着决定性作用。为了研究斜盘倾角对液压力矩的影响，利用AMESim进行对比仿真分析，系统参数如下：增压油箱压力0.5 MPa；系统压力28 MPa，斜盘倾角分别设为0°，6°，12°，18°，主轴转速7000 r/min，仿真时间0.2 s，采样间隔0.0001 s。

仿真结果如图13所示。分别为不同斜盘倾角条件下液压力矩大小的周期变化图像。

由结果可知，当斜盘倾角不为0°(不在泵的死区内)时，液压力矩的大小与斜盘倾角的关系不大。

图13 不同斜盘倾角液压力矩Mb大小

4 结论

通过对非对称轴向柱塞泵斜盘力矩大小的数学计算及在AMESim中的仿真验证可得出如下结论：

(1) 与对称配流结构相比，非对称配流结构的柱塞泵在高压工况下工作时，其液压力矩不可忽略，且在斜盘承受力矩中占主导地位；

(2) 在高压工况下，斜盘承受液压力矩的大小主要由系统的压力决定，与斜盘倾角大小关系不大(斜盘处于死区位置除外)。