斜盘轴向柱塞泵配流副流固耦合润滑机理研究

， , ， ，

(1. 上海工程技术大学机械与汽车工程学院， 上海 201620；2. 兰州理工大学能源与动力工程学院， 甘肃兰州 730000；3. 上海工程技术大学城市轨道交通学院， 上海 201620)

引言

配流盘是轴向柱塞泵的关键零件之一,在高速高压工作条件下,作用在配流副零部件上的高压油产生的压力将使零件发生弹性变形[1]。配流副正常工作时，配流盘在高压条件下的弹性变形与油膜厚度属同一量级，配流盘接触表面的弹性变形大小会直接影响到油膜厚度，而产生的弹性变形又会使油膜厚度和压力分布不均匀，势必对配流副的工作状态和润滑特性带来一系列影响[2-3]。WANG X[4-5]对类似于配流副工作机理的推力轴承进行了其密封带材料特性的研究以及弹性变形对油腔压力、承载力及泄漏量的影响分析。郑炜等[6]对63CY14-1B型轴向柱塞泵的配流盘在压力场下的变形进行了有限元计算,结果指出,工作时配流盘表面产生十分明显的翘曲变形,高压区变形最为严重,配流盘表面的最大变形为25 μm,最小变形为10.25 μm,造成配流副间局部区域直接接触产生偏磨,但是没有具体指出不同条件下的变形情况。配流盘间油膜作用力使配流盘产生弹性变形，而配流盘的变形又会影响油膜的压力，因此需要综合考虑流固耦合对配流盘性能的影响。传统地把配流盘等效为刚体的研究方法不能准确反映工作时实际变形状态，使配流副实际工作情况与理论设计结论产生偏差，所以本研究利用弹性流体润滑理论[7]对柱塞泵的配流盘在不同材料以及不同缸体转速、缸体倾角、液压油黏度、配流副油膜厚度、配流副密封带宽度下产生的变形量进行分析比较，并对配流副的润滑影响进行讨论。

1 配流副流固耦合模型的建立

油膜的压力、厚度充分的体现柱塞泵配流盘的性能，而油膜压力及厚度取决于柱塞泵负荷、转速、配流盘的几何形状以及配流盘表面的变形量。考虑到计算量巨大，本研究通过联立润滑油膜的动压(雷诺方程)、油膜厚度方程和弹性变形方程来进行差分迭代求解配流副的弹性变化值及其性能参数，进而描述其润滑机理。

1.1 倾斜缸体配流副模型

图1所示为倾斜缸体配流副模型：缸体相对配流盘发生倾斜，高压侧油膜较薄，低压侧油膜较厚，通过腰型槽中心线y轴，另一垂直方向z轴进行象限划分。其中，h0为初始油膜厚度；h1为最小油膜厚度；h2为最大油膜厚度；R1为配流盘内密封带内径为30 mm；R2为内密封带外径为40 mm；R3为外密封带内径为50 mm；R4为外密封带外径为60 mm。

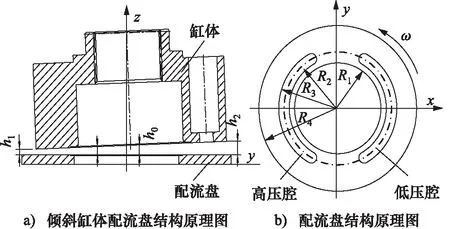
图1 倾斜缸体配流副模型

1.2 控制方程

为了建立完整的数学模型，在满足实际工程要求的基础上对模型条件进行简化，现引入如下的假设[8-9]:

(1) 和油膜相邻的固体表面曲率半径远大于油膜厚度；

(2) 油膜厚度方向压力保持不变；

(3) 润滑油为牛顿流体，并为连续的层流动；

(4) 油膜为等温，并且忽略油膜黏压效应，密压效应；

(5) 与黏性剪切力相比,油膜受到的惯性力和其它体积力可以忽略不计；

(6) 配流盘材料为线性弹性体。

配流副润滑模型的控制方程包括等温弹流体动力润滑的雷诺方程和油膜厚度方程。雷诺方程是在假设润滑油吸附于缸体与配流盘表面的基础上建立的。经过简化的二维极坐标雷诺方程如下[10]：

(1)

式中，p—— 油膜压力

μ—— 润滑油黏度

ω—— 缸体转动角速度

r—— 油膜上某一点相对中心半径

h—— 油膜厚度

θ—— 配流盘上某一点周向角度

配流副油膜厚度与油膜压力分布相互耦合。本研究通过有限差分法对极坐标下的雷诺方程(1)进行离散化，其离散表达式：

(2)

进行离散化后可得：

其中：

(4)

(5)

(6)

(7)

E=A+B+C+D

(8)

(9)

根据弹性流体润滑理论，沿油膜厚度方向上的压力保持不变，润滑油是连续的层流流动，配流盘在变形时会发生表面沉陷，导致润滑油填充沉陷处，油膜在此处增加，于是考虑弹性变形的油膜厚度方程为[9]：

(10)

h0—— 初始油膜厚度

r—— 配流盘上某一点对应半径

θ—— 配流盘任一位置相对初始位置角度

φ—— 缸体倾斜角度

1.3 弹性变形量方程

配流盘一般是由经过特殊处理的金属、合金材料构成。由于配流机构为经过表面处理的不锈钢,具有较大的刚度,可以忽略缸体的变形,仅考虑配流盘的变形。于是可以将配流面材料视为弹性体,配流盘内部应力、应变也满足弹性力学的基本规律。

基于此，本研究引用一种关于弹性基础木梁的 Winkler 假定[2，11]。假定认为，梁在弯曲时受到基础的连续分布的反作用力的作用。各点上反作用力的强度(单位长度上的力)与木梁在该点的位移成正比，也就是把配流面的材料设想为无穷多个紧密排列的弹簧，弹簧一端固定在刚性的配流盘上，另一端承受油膜压力，每个弹簧在压力作用下的位移相互独立，则配流面材料各节点的弹性变形量经计算可表达为[8-9]：

(11)

式中，t—— 配流面材料厚度

ν—— 材料泊松比

E—— 材料弹性模量

本研究选择斜盘式柱塞泵配流盘由氮化钢或者铜合金材料构成，进而通过不同配流盘材料进行对比分析[2,12]。

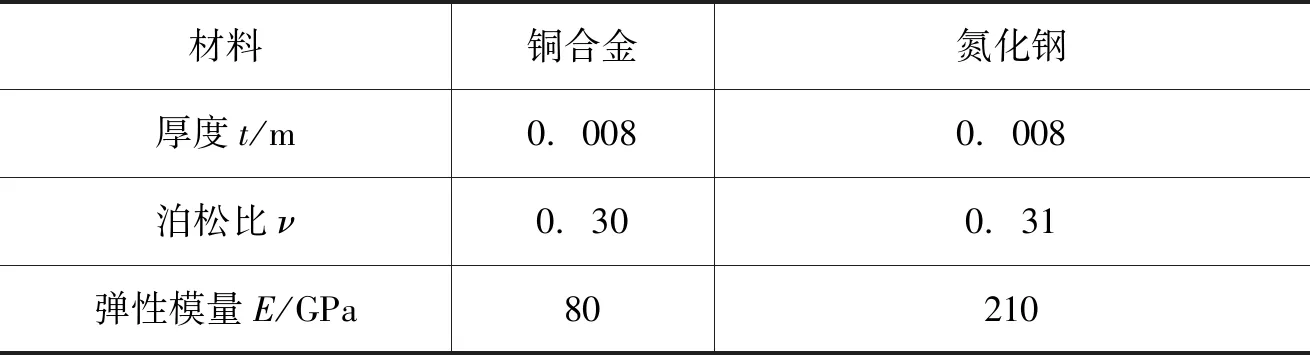
表1 材料参数

1.4 边界条件

(1) 斜盘式轴向柱塞泵配流副中配流盘密封带内外侧初始压力设为大气压:p0=0.101325 MPa；腰形槽高压油口为实际工况压力设为p；低压油口压力值同样设为大气压。

p(r=r1,θ)=p0

p(r=r4,θ)=p0

p(r2≤r≤r3,196°≤θ≤344°)=p

p(r2≤r≤r3,16°≤θ≤164°)=p0

(12)

(2) 配流盘工作接触面是圆环形状，在0°和360°位置采用循环周期条件：

p(r,2π)=p(r,0)

H(r,2π)=p(r,0)

(13)

(3) 若油膜出现破裂，在破裂处边界条件为p=0。

2 数值计算结果与分析

通过FORTRAN编译器对上述离散化公式进行迭代求解，并将结果数据导入MATLAB中，得到图2所示图形[8-9]。

图2显示油膜压力的分布是非线性的，且油膜厚度分布有一定偏置。是由于高低压区的存在，在负载转矩下导致油膜厚度发生动态变化。油膜在顶部较厚，底部较薄，低压区油膜厚度较大。同时，配流盘在高压工况下产生一定的翘曲变形，应变发生在高压配流窗口腰型槽的外侧，变形方向主要是在径向，最大变形量出现在高压区腰形窗口外侧的内壁到配流盘外缘区域内，而且配流盘高压侧外密封带区域变形最大，配流盘低压侧外密封带区域变形最小。

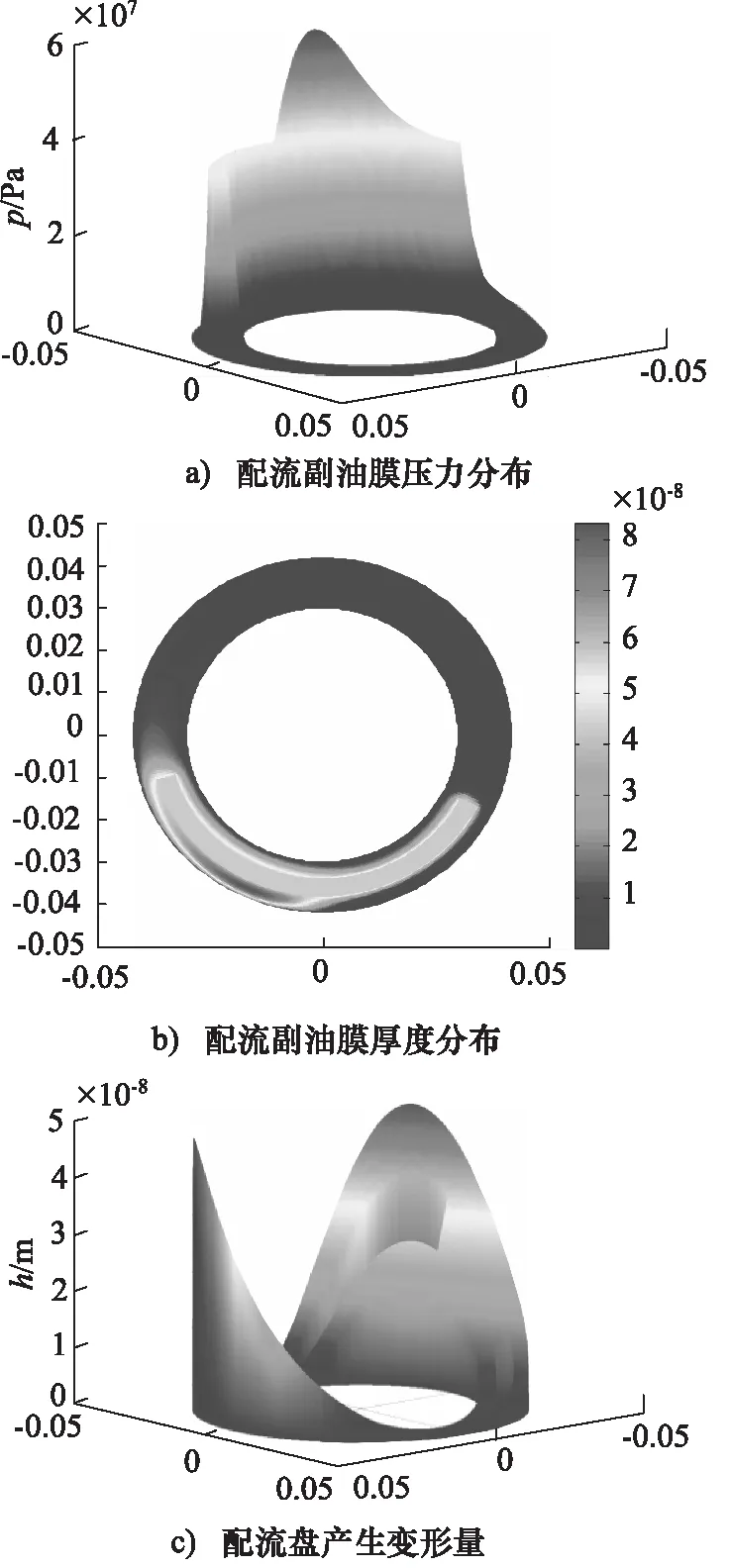
图2 等温弹性体配流盘变形情形

2.1 不同材料下配流盘的变形量

在工作压力p=35 MPa，缸体倾角α=0.004°，初始压力为标准气压，初始油膜厚度h0=0.0325 m，油液黏度μ=0.036572 Pa·s,密封带宽度l=0.0121 m,转速ω=3000 r/min，配流盘的配流面材料分别在氮化钢、铜合金的条件下，改变材料厚度、材料类型进行数据求解分析。

通过图3进行分析，随着表面材料厚度的增加，配流盘表面的变形量亦不断增加，且呈类似正比线性关系。对于铜合金材料的配流面，厚度增加8倍，变形量增加80倍；对于氮化钢的配流面，厚度增加8倍，变形量增加8倍，主要原因是氮化钢的弹性模量比铜合金大，氮化钢约为铜合金弹性模量的3倍，而弹性模量是衡量物体抵抗弹性变形能力大小的尺度，其值越大，使材料发生一定弹性变形的应力也越大，对应的变形越小。

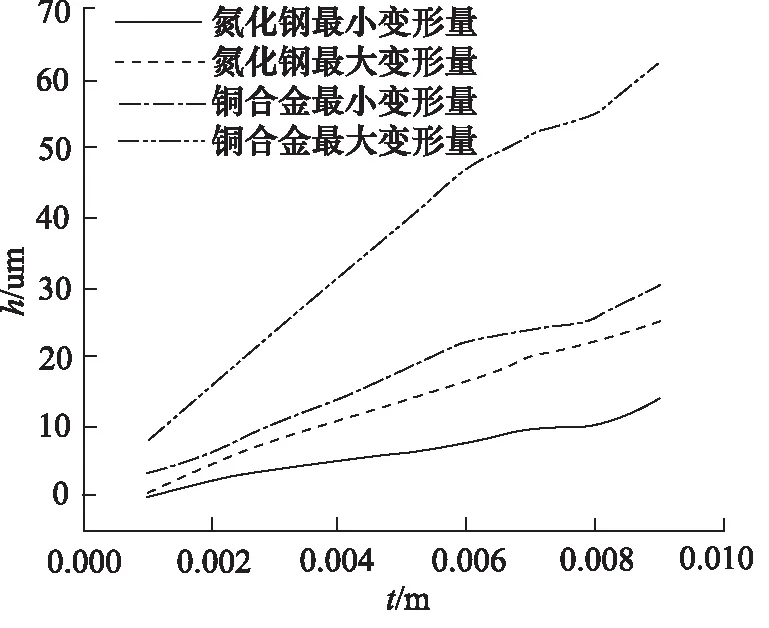
图3 不同配流盘材料的变形量

按照设计配流盘的要求和配流副润滑的特性，配流盘变形量越小越好，也即材料厚度变小，但是配流副在工作过程中由于摩擦力做功所产生的高温以及同时产生的磨屑堆积聚集在摩擦副的表面，将加速配流副磨损的过程，当温度和表面磨损情况达到一定程度时，会形成较为严重的黏着磨损，从接触表面脱离的金属粒子的拖动和微小的表面之间不规则性的摩擦，会产生磨粒磨损。若增加配流面的厚度，由图3可知必然会增大变形量，影响配流效率。故在选择材料厚度时需综合考虑各种因素。

2.2 不同工况下配流盘的变形量

配流盘的配流面选用铜合金材料，缸体转速ω为1000， 2000， 3000， 4000， 5000， 6000 r/min；缸体倾角α为0.001°， 0.0002°， 0.003°， 0.004°， 0.005°， 0.006°；液压油黏度μ为0.016572， 0.026572， 0.036572， 0.046572， 0.056572， 0.066572 Pa·s；初始油膜厚度h0为0.02， 0.023， 0.026， 0.029， 0.032， 0.035 mm；密封带宽度l为0.0121， 0.0131， 0.0141， 0.0151， 0.0161， 0.0171 m，分别进行数值计算求得配流盘弹性变形量如图4所示。限于篇幅以及为易于进行比较，图4中横坐标仅代表不同参数的变化。

由图4计算结果和图形显示：在等温条件下，转速、缸体倾角、液压油黏度、密封带宽度和变形量成正比，根据本研究设定条件下产生的数据在图4显示下，各参数变化依次产生最大变形量是最小变形量的35倍、5倍、16倍、36倍，初始油膜厚度和变形量成反比。油膜厚度对变形量的影响及敏感度最大。而缸体倾角、液压油黏度、转速、密封带宽度对变形量的影响不太明显。

图4 各种工况产生的变形量

配流盘的最大和最小变形量都随转速增加而不断增大，6000 r/min产生的变形量是1000 r/min产生变形量的近35倍，随着转速的增加，产生变形量的增幅趋于下降。润滑油的黏度通过油膜厚度的大小影响油膜的压力，同时对柱塞泵缸体、配流盘产生轴向的作用力，会造成一定的变形，另一方面，黏度也影响着摩擦力的大小，高黏度的润滑油不但会引起很大的摩擦损失和发热，而且难以进行散热，这样摩擦温度的升高就可能导致油膜破裂和表面磨损。图4中可以看出在黏度较低时，配流盘工作时产生的变形量很低，在常压下,压强对润滑油黏度的影响很小,一般可以忽略不计。

同时，由图4数据显示：密封带宽度因素产生的最大变形量的增幅比最小变形量产生增幅更快，且呈现非线性增加。初始油膜厚度在0.02 mm时产生的变形量是膜厚0.035 mm产生变形量的近50倍。最大变形量是最小变形量的2倍左右。当油膜厚度大于0.026 mm继续增大时，增加的变形量可以忽略，但此时由于油膜厚度过大，将会降低柱塞泵的配流效率，当考虑温度等其他条件时，可以合理推断最佳的油膜厚度将会更小，所以合理的油膜厚度是柱塞泵高效率配流的重要因素。

3 结论

基于Winkler假定结合弹流润滑理论，建立了斜盘式轴向柱塞泵配流副的物理模型，进行流固耦合计算，并利用Fortran编译器求解了所建立的配流盘的控制方程。分析了配流盘的各参数及配流盘表面材料对配流盘变形的关系，并分析产生变形后对配流副润滑的影响，结果表明：

(1) 油膜压力的分布是非线性的，且油膜厚度分布有一定偏置,配流盘表面的弹性变形受局部压力峰值影响较大。配流盘应力主要集中在高压配流窗口周围，应变发生在高压配流窗口腰型槽的外侧，变形方向主要在径向，最大变形量出现在高压区腰形窗口外侧的内壁到配流盘外缘区域内。故对该区域应该进行特殊的处理，减少偏磨泄漏现象的发生；

(2) 对于采用的分别由不同材料构成的配流盘，随着材料厚度的增加，配流盘表面的变形量亦不断增加，且不同材料在相同工作条件下表现出的变形有着巨大差异。综合材料的弹性模量、材料磨损、变形与厚度的类似正比线性关系、考虑工艺的可行性及经济性问题，结合本研究中假定的配流盘总厚度，确定配流面厚度一般为0.006～0.008 m；

(3) 在设定的条件下，在油膜厚度大于0.02～0.03 mm继续增大时，所增加的变形量很小，可以忽略对配流副润滑特性的影响；

(4) 配流盘在不同转速、缸体倾角、液压油黏度、初始油膜厚度、密封带宽度下表现出不同的变形量，尤其是油膜厚度、密封带宽度对变形量的影响更大，通过改变上述参数可以减少配流盘变形量的产生，进而提高配流盘的润滑性能。