空间站柔性太阳电池翼模态分析及基频优化
2019-04-22郭其威唐国安
臧 旭, 吴 松, 郭其威, 唐国安
(1. 复旦大学 航空航天系,上海 200433; 2. 上海宇航系统工程研究所,上海 201109)
空间站需要大面积且能在火箭中折叠装载的大型太阳电池翼为其提供主要动力来源[1-2]。我国空间站电池翼借鉴国际空间站成功经验,采用“Mast”+“Blanket”柔性电池翼的设计方案[3],初始顶部收藏箱与底部收藏箱重叠在一起,如图1收拢状态所示。当接到展开指令后,伸展机构在电机驱动下沿垂直方向伸展,带动柔性阵面展开,导向机构限制阵面的面外运动,直至最后一块基板展开,张紧机构施加预紧使柔性阵面张紧,如图1展开状态所示。
国际空间站电池翼展开面积超过100 m2,基频在0.1 Hz以下,并且低阶模态密集度高[3~5]。柔性电池翼的频率特性是空间站姿态控制系统设计的关键指标[6],20世纪80年代末在国际空间站研制过程中,柔性翼动力学参数多通过解析法获取,Sasan等[7]以带有预紧力的国际空间站桁架为研究对象,采用考虑转动惯量的梁振动方程,计算得到了桁架的展开频率。Bosela[8]考虑了含有预紧力的柔性翼阵面及桁架的力学特性,运用伽辽金法得到柔性电池翼模态参数。Carney等[9-10]分别给出了0 g和1 g状态柔性太阳电池翼频率半解析解。随着计算机技术的迅猛发展,有限元法已成为预示大型挠性结构模态参数的主要手段[11-13]。Laible等[14]将国际空间站2 A电池翼在轨辨识数据与仿真数据进行了对比,分析表明柔性电池翼发生几何非线性变形,该非线性是电池翼模态预测误差产生的主要原因。郭其威等[15]将加载均匀张力的柔性阵面等效为弦,给出了伸展机构临界屈曲载荷与整翼基频关系,并通过有限元法获取了伸展机构临界屈曲载荷。

图1 空间站柔性太阳翼示意图Fig.1 The flexible solar array diagram
本文综合考虑柔性电池翼在张力作用下的几何非线性变形,阐明了非线性静力分析不易收敛的机理,通过温度应力实现张力模拟[12-13],采用线性初值加非线性迭代修正两步法,获取了即保证非线性计算收敛又满足工程张力设计值的温度变化量,并依据整翼非线性静力矩阵获取空间站柔性太阳电池翼模态参数。
1 柔性太阳电池翼建模
在研柔性太阳电池翼方案由柔性阵面、张紧机构、伸展机构、收藏箱、收藏桶和驱动机构组成,有限元模型如图2所示,各部件尺寸及材料参数,见表1。忽略伸展机构机构间隙影响,将其简化为一根细长梁。伸展机构、收藏箱、收藏桶和驱动机构均采用两结点梁单元模拟,柔性阵面采用四结点壳单元模拟。张紧机构也采用两节点梁单元模拟,为协调梁单元与壳单元的连接自由度,张紧机构与柔性阵面采用刚性约束连接,并约束6个方向的自由度。

图2 柔性太阳翼有限元模型Fig.2 The flexible solar array finite element model表1 尺寸及材料参数汇总Tab.1 Summary of dimensions and material parameters

驱动机构收藏桶收藏箱伸展机构张紧机构柔性阵面单元类型梁单元梁单元梁单元梁单元梁单元壳单元单元数/个55521081 260弹性模量/GPa7070400702103泊松比0.30.30.30.30.30.3质量/kg30804×2085
2 柔性太阳电池翼模态分析方法
柔性太阳电池翼受到张紧机构张力F作用,柔性阵面刚度因张力作用而发生改变,其形式可表示为K=K0+FK1,其中K0为柔性阵面初始刚度,K1为K关于张力F的导数矩阵。柔性阵面初始刚度K0极低,远小于由张紧力引入的附加刚度FK1,因此张紧力是决定柔性太阳电池翼基频的重要因素。柔性太阳电池翼四个张紧机构均设置在顶部收藏箱上,建模时通过在与顶部收藏箱连接的张紧机构梁单元上施加降温实现张紧机构张力加载,如图2所示。为考虑整翼几何非线性变形及预应力影响,先进行非线性静力分析,获取张力作用下的整翼刚度矩阵K0+FK1,并以此刚度矩阵为基础通过模态分析获取整翼预应力状态动力学参数。

图3 收藏箱几何变形示意图Fig.3 Collecting box geometric distortion diagram
按设计要求模拟张紧机构张力F的温度变化值的设置是建立空间站柔性电池翼有限元模型的关键。太阳电池翼收藏箱在张紧力作用下产生变形,导致收藏箱在与内、外张紧机构连接处变形不一致δ1≠δ2(如图3所示),此时存在两个问题:①顶部收藏箱变形δ2>δ1,外部张紧机构原本由温度应力获得的变形部分被收藏箱变形所抵消,为保证F1=F2=F的设计要求,则在外张紧机构上施加的温度变化值T2必须大于内张紧机构上的温度变化值T1;②受张紧力影响底部收藏箱也发生变形,在张紧机构上施加相同的温度变化初值,底部收藏箱外部张紧绳存在受压F4<0的可能性,导致非线性计算不收敛。为解决上述问题,本文先采用影响系数法获取线性温度变化初值,再通过非线性迭代修正获取满足F1=F2=F要求的温度变化值T1、T2。
2.1 线性初值获取
为使内外张紧机构张力满足F1=F2=F的设计要求,需在顶部收藏箱内外张紧机构梁单元上施加不同的温度变化值T1、T2,且T1小于T2。在线性情况下,内外张紧机构张力F1和F2可表示为关于T1、T2的线性方程:
(1)
为便于计算令张紧机构梁单元热膨胀系数α=1/℃,式(1)的系数矩阵可通过影响系数法获取,即假设αT1=1、αT2=0,代入整翼有限元进行线性求解,F11、F21分别对应为顶部收藏箱内外张紧机构单元力,同理假设αT1=0、αT2=1,可得到F12、F22。此时令内外张紧机构张力F1=F2=F,求解线性方程组(1)可得到线性情况下,使内外张紧力均为F时需加载的温度变化值T10、T20。
2.2 非线性迭代修正
在非线性情况下,顶部收藏箱内外张紧机构张力F1和F2通常表示为关于温度变化值T1、T2的非线性方程:
(2)
方程组(2)通常是隐式的,不易直接求解,可通过线性求解得到的温度变化值T10、T20为初值,对式(2)作Taylor展开,并保留一阶项得到:
(3)
式中:矩阵H可采用差分方法计算获得,令F1=F2=F,代入式(3)得到新的温度变化值T11、T21,并将其代入有限元模型进行非线性静力求解,检查顶部收藏箱内外张紧机构单元力是否为F,若仍有偏差,则以T11、T21为初值重复上述步骤迭代修正,直到内外张紧机构单元力满足精度要求。实践表明,仅需一次迭代即可得到足够精度的张紧机构张力。具体步骤如下:
(1)以线性求解得到的温度变化值T10、T20为初值,代入有限元模型进行非线性静力求解,输出顶部收藏箱内外张紧机构单元力分别为f1(T10,T20),f2(T10,T20);
(2)令T1=(1+η)T10、T2=T20,将上述温度变化值代入有限元模型进行求解,输出顶部收藏箱内外张紧机构单元力分别为f1[(1+η)T10,T20],f2[(1+η)T10,T20];
(3)令T1=T10、T2=(1+η)T20,将上述温度变化值代入有限元模型进行求解,输出顶部收藏箱内外张紧机构单元力分别为f1[T10,(1+η)T20],f2[T10,(1+η)T20];
(4)计算矩阵H的各个分量
(4)
(5)求解线性代数方程(3),得到得到温度变化值T11、T21,代入有限元模型校核张紧机构单元力;
(6)以温度变化值T11、T21作为初值,重复(1)~(5)步直到内外张紧机构单元力满足精度要求为止。
3 柔性太阳电池翼动力学特性
假设张紧机构张力F=30 N,柔性太阳电池翼非线性静力及模态分析结果如表2、表3所示,结果表明电池翼底部收藏箱内外张紧机构张力不均匀。柔性太阳电池翼一阶弯曲振型表明底部收藏箱外部张紧力不足,柔性阵面应力不均匀导致阵面外侧刚度变小、容易蜷曲,如图4所示。为了验证均匀张力对柔性电池翼基频的改善,在电池翼底部收藏箱外侧各增加一个张紧机构,分析表明张紧机构张力相同,整翼基频明显提高,振型如图5所示,因此建议设计中应采取相应改进措施。

表2 非线性静力计算结果Tab.2 Nonlinear static calculation results

表3 模态计算结果Tab.3 Modal calculation results

图4 非均匀张力一阶弯曲振型Fig.4 The first order bending mode of non-uniform tension

图5 均匀张力一阶弯曲振型Fig.5 The first order bending mode of uniform tension
柔性电池翼的基频通过张紧机构预应力施加于柔性阵面实现,柔性阵面受拉绷紧,伸展机构受压并与收藏箱提供支撑边界。在均匀张力作用下,柔性阵面一阶固有模态呈弯曲变形,由于阵面为薄膜结构,其一阶频率及振型与受拉弦近似,可按弦理论近似计算:
(5)
式中:ρb为阵面线密度;lb为阵面长度;柔性阵面基频从0 Hz开始;随张紧力F增大而逐渐提高。阵面张紧力反作用于伸展机构的轴压为4F,伸展机构简化为细长梁结构,考虑柔性阵面质量影响伸展机构承受轴压状态下自由振动频率:
(6)
式中:ρm为伸展机构线密度,伸展机构基频随张紧力F增大而逐渐下降,并在张紧力合力4F超过伸展机构屈曲载荷Pcr时下降至0 Hz,因此必定存在张紧力4F/Pcr的最优取值,如图6所示。

图6 伸展机构及阵面基频随4F/Pcr比值变化Fig.6 Stretchable mechanism and array base frequency change with 4F/Pcr

图7 柔性太阳电池翼基频随4F/Pcr比值变化Fig.7 The flexible solar array base frequency change with 4F/Pcr
柔性阵面张力与伸展机构屈曲载荷比值不同,柔性电池翼整翼基频及振型也呈现出不同的表现形式,如图7所示。比值较小时,柔性阵面尚未张紧,基频较低,整翼振型表现为阵面大幅振动,伸展机构几乎不动,如图8所示;随着比值升高,整翼基频逐渐提高,并且在张紧力4F到达伸展机构屈曲载荷Pcr的10%时,到达整翼基频的最优点,此时整翼振型表现为阵面与伸展机构振幅相当,如图9所示;当越过最优点后,随着比值继续提高整翼基频不断下降,并在张紧力4F到达伸展机构屈曲载荷Pcr时,伸展机构发生屈曲,整翼基频下降为0,此时张力4F=1 720 N,即伸展机构临界屈曲载荷为Pcr=1 720 N。
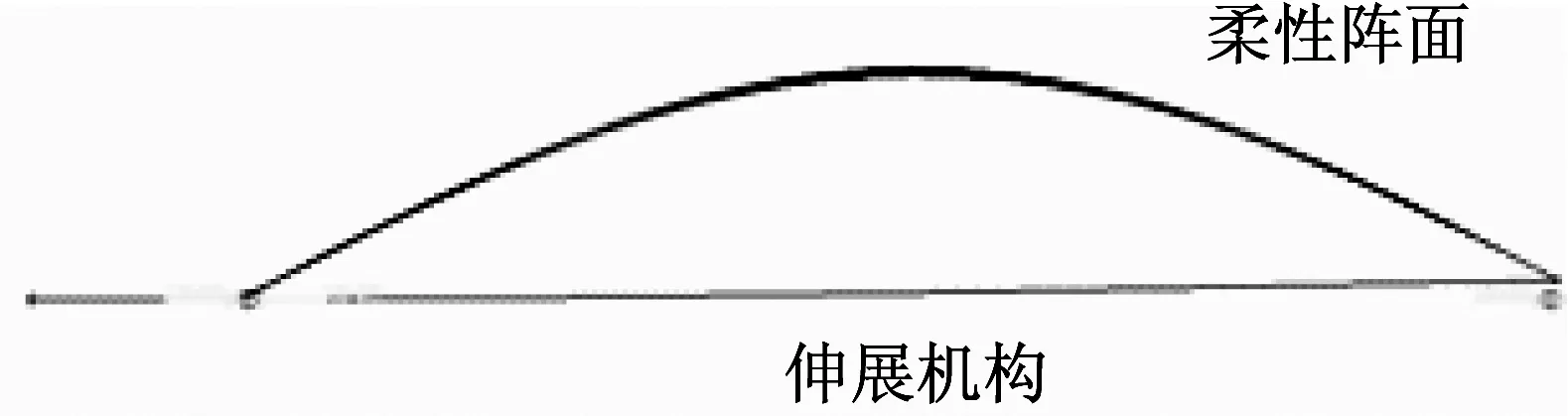
图8 4F/Pcr=0.01整翼振型示意图Fig.8 4F/Pcr=0.01 solar array vinration diagram

图9 4F/Pcr=0.1整翼振型示意图Fig.9 4F/Pcr=0.1 solar array vinration diagram
4 总 结
本文建立空间站柔性太阳电池翼有限元模型,采用温度应力模拟柔性阵面张紧力加载,并通过线性初值加非线性迭代修正,获取使电池翼内外张紧机构张力相同的温度变化值,解决了由于收藏箱变形导致的柔性阵面非线性静力计算迭代不易收敛的问题。根据非线性静力分析获取整翼预紧力状态刚度矩阵,以此刚度矩阵为基础开展柔性太阳电池翼模态分析,并获得具有实际工程设计意义的结论如下:
(1)在电池翼底部收藏箱外部各增加一套张紧机构,可有效保证全部张紧绳张力相同,阵面张力均匀,整翼基频明显提高。
(2)柔性电池翼基频受张紧力影响较大,假设伸展机构无限刚,张紧力越大电池翼基频越大。而实际情况下伸展机构的刚度由其包络直径、纵杆尺寸等因素决定,伸展机构基频随张紧力增大而逐渐下降,且张紧力加载受到伸展机构临界屈曲载荷限制,分析表明张紧力4F到达伸展机构屈曲载荷Pcr的10%时,到达整翼基频的最优点。
