多股簧非线性响应模型及其影响研究
2019-04-22丁传俊张相炎
丁传俊, 刘 宁, 张相炎
(南京理工大学 机械工程学院,南京 210094)
多股螺旋弹簧(简称多股簧,图1)是由多股钢丝拧成钢索卷制而成的圆柱螺旋弹簧。和普通单股弹簧相比,多股簧抗冲击性能好、吸振能力强、具有较大的刚度和非线性阻尼、寿命长,常被用作小口径自动武器的缓冲复进簧[1]。
多股簧响应模型是描述多股簧在静、动态载荷下恢复力与变形量之间关系的数学模型。目前使用较多的响应模型有双折线模型[2]和基于现象模型的Bouc-Wen迟滞模型及其修正模型[3](简称BW模型)。虽然以上两种模型可以较好地描述多股簧的响应特性,但构建模型时的测试速度都很低,并没有考虑到自动武器发射过程中的高速、冲击等特性,应用于自动武器动力学计算时将会产生一定的误差[4-5]。

图1 多股簧Fig.1 A stranded wire helical spring
王时龙等[6-7]通过建立两端并圈的多股簧有限元模型,研究了多股簧受冲击时弹簧各质点的运动形式,结论认为如果冲击速度过大,弹簧簧圈会发生压并现象;田波[8]测试了不同冲击速度下多股簧的刚度和阻尼,发现高速冲击时多股簧的阻尼系数是自由衰减时的6倍。虽然以上学者进行了多股簧的冲击试验,但是并没有将多股簧冲击试验结果应用于武器的缓冲复进计算。
本文根据多股簧静态、低速动态和冲击试验的测试结果对多股簧静态、低速动态恢复力模型进行了参数辨识,并提出了计及冲击端速度的广义修正归一化Bouc-Wen迟滞模型(简称广义BW模型)。通过建立火炮自动机发射动力学有限元模型,同时考虑内弹道和导气装置的耦合过程并将以上三种弹簧模型应用于自动机动力学仿真计算,本文验证了当前耦合计算模型、自动机有限元模型的准确性。通过对比三个多股簧响应模型的计算结果,本文发现,双折线模型的滞回耗能较大、弹簧恢复力较小,复进时自动机的传动框不能及时复进到位;BW模型和广义BW模型都能够使自动机的传动框复进到位,且广义BW模型的理论射速高于BW模型。
1 多股簧非线性响应模型及其试验
1.1 双折线模型
双折线模型采用一组分段线性函数来描述多股簧的迟滞响应。作为一种简单迟滞模型,主要用于自动武器前期的概念设计。图2为万能拉压试验机所输出的某拨弹板簧的恢复力曲线(加载速度为0.8 mm/s)。从图中可以看出,当轴向位移加载到一定程度时,由于簧丝之间发生了紧密接触和摩擦,多股簧恢复力有明显的拧紧点,且拧紧点前后弹簧的静态刚度有一定差异;卸载时多股簧簧丝逐渐放松,卸载阶段弹簧的放松点不太明显,有些较为“松软”的多股簧甚至没有放松点。
双折线模型的恢复力为:
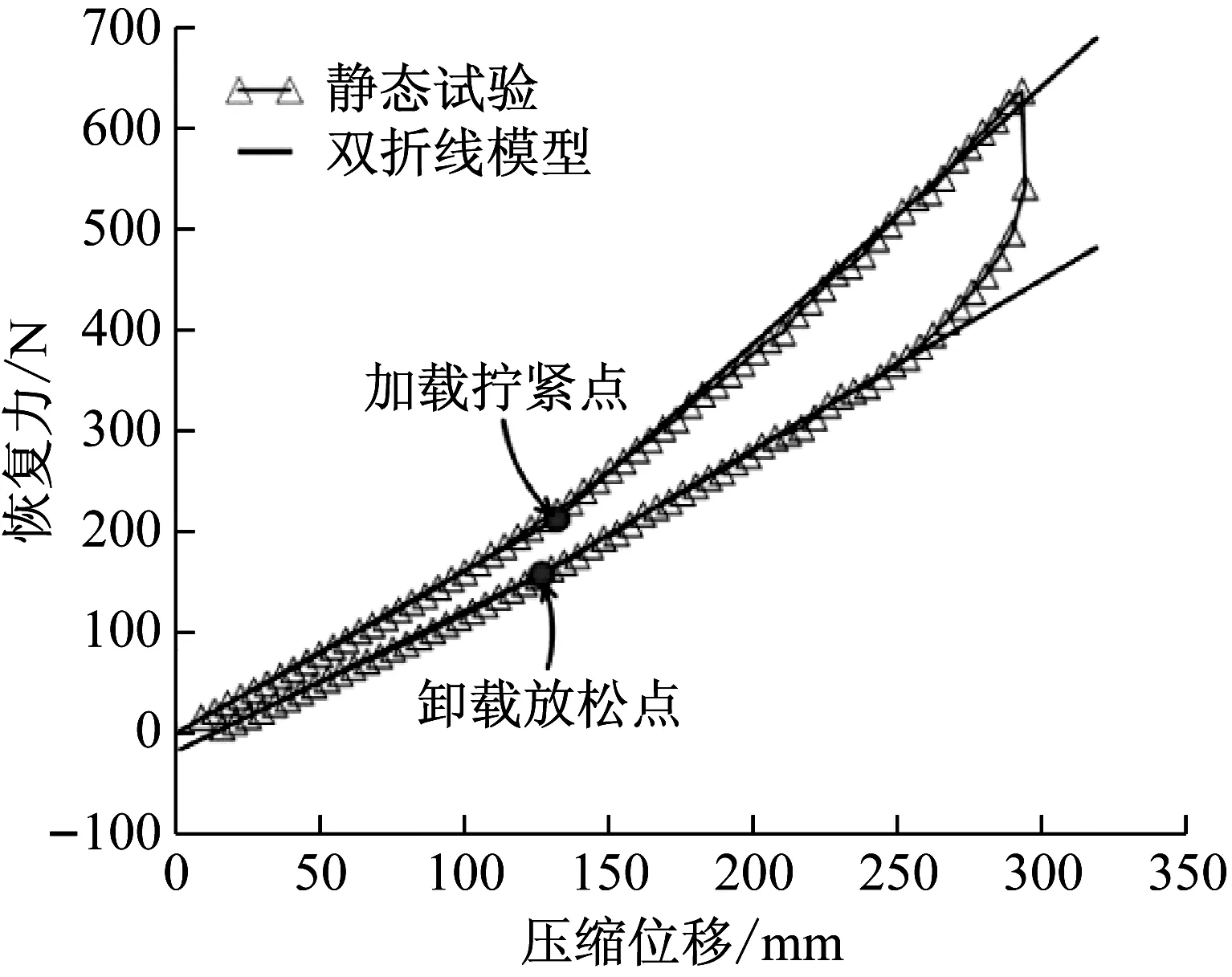
图2 多股簧的静态响应Fig.2 Measured static response of stranded wire helical spring
(1)
式中:F(x)、F0分别为多股簧的恢复力和预压力,ca0、ca1、cb0、cb1分别弹簧各段的静态刚度,xap、xbp分别为加载时的拧紧点和卸载时的放松点。
一般情况下自动武器中的多股簧其工作范围都在加载拧紧点之上,所以弹簧的恢复力可以用拧紧点后的两条直线来描述。虽然静态试验曲线形成了非对称滞回曲线,但这种滞回曲线并不能用BW模型及其修正模型来描述,其原因是静态试验的加载速度为定值且存在加载和卸载时的突变。多股簧的双折线模型可以采用最小二乘法求解,由于模型比较简单,所获得的参数有着较高的精度。
1.2 修正归一化Bouc-Wen模型(BW模型)
Zhao等[3]提出使用修正归一化BW模型来表示多股簧的力/位移响应特性。该模型作为非线性微分模型将弹性元件的恢复力分解为弹性部分和纯迟滞部分,并将迟滞量以微分方程解的形式给出。由于BW模型及其修正模型能够同时描述多股簧的刚度和迟滞阻尼效应,响应曲线比较光滑,且在加载和卸载的各个区域内都能很好地与试验结果吻合,因此能以较高的精度反映出多股簧的非线性动态特性并获得了广泛的应用。BW模型的表达式为:
(2)
式中:x(t)、t分别为位移和时间;FE和FA分别是恢复力的非线性弹性部分和非线性放大部分;kEi和kAi分别是非线性刚度系数和非线性放大因子,N是多项式的阶数,一般取2阶或3阶;ω(t)为纯迟滞部分,对于任意的x(t)和t,都有|ω(t)|≤1;ρ、σ、n为控制纯迟滞部分ω(t)曲线形状的迟滞三参数。Ikhouane等[9]进一步指出归一化BW模型只有在满足ρ>0、σ≥0.5时才有物理意义,而且在实际应用中,若n<1则会使微分方程的右端出现无限大的量,从而导致计算发散。
图3即为使用动态疲劳试验机测得的某拨弹板簧恢复力曲线。从图中可以看出,动态情况下多股簧的响应曲线也是非对称滞回曲线;和静态试验结果相比,动态加载时弹簧的回弹力所有增加。需要指出的是使用动态试验机测试多股簧的响应时,仪器的加载速度和幅值都比较有限,例如当前试验条件下,试验机的最大加载速度、幅值分别是214 mm/s,45 mm。
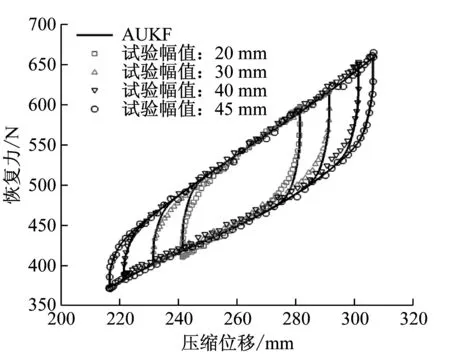
图3 多股簧的动态响应Fig.3 Measured dynamic response of stranded wire helical spring
多股簧的BW模型以及本文将要提出的广义BW模型是一个多参数的非线性迟滞模型,对其参数辨识存在一定的难度,目前广泛采用的辨识方法大体可以分为两类:解析算法和迭代算法。其中常用的解析算法有三步法[3]、极限环法[9]等,这类方法大多数都要求在求解前对试验数据进行平滑降噪和迟滞量分离处理,优点在于求解速度快;迭代算法主要有滤波算法[10]、粒子云算法[11]、差分演化算法[12]等,这些算法一般不需要对数据进行预处理,求解参数数量不受限制,计算过程抗噪声性能较强且参数辨识结果精度高,但求解过程比较耗时。图3中的黑色实线即为本文使用自适应无迹卡尔曼滤波算法[13-14](AUKF)预测出的多股簧力/位移响应。
1.3 广义修正归一化Bouc-Wen模型(广义BW模型)
自动武器中的多股簧在使用时主要承受高速冲击载荷,弹簧的变形速度很快。在这种变形速度下,由于弹簧自身有质量和惯性,其内部各质点的运动速度沿轴向不再是线性分布,而是以纵波的形式向固定端传递并在固定端反射[7]。由于以上两个模型不能反映多股簧在自动武器中的实际工作状态,因此本文提出计及冲击端速度的广义BW模型。广义BW模型不再将弹性部分和非线性放大因子中的系数当做定值,而视其为冲击端速度v的二阶或者三阶函数。一般情况下,通过三到四次不同冲击速度的测量即可确定模型中的参数。广义BW模型的表达式为:
(3)
式中:kEi(v)和kAi(v)分别是计及冲击端速度的非线性刚度系数和非线性放大因子。图4(a)即为重庆大学多股簧课题组[7]研制的冲击试验装置,其中A为冲击试验所用的高压气源,B为冲击结构主体(包括多股簧固定装置、冲击体和阀门等),C为测量簧圈运动情况所用的光电传感器。图4(b)为当冲击体速度为17.65 m/s时某复进装置多股簧的冲击响应情况。从图中可以看出,冲击时多股簧刚度的非线性特性更为明显,当压缩变形量为0.4 m时弹簧的恢复力约为静态测试情况下的1.5倍。图4(b)中的黑色曲线即为本文使用反向差分演化算法[15](ODE)预测出的多股簧的力/位移响应。

(a) 多股簧冲击试验装置
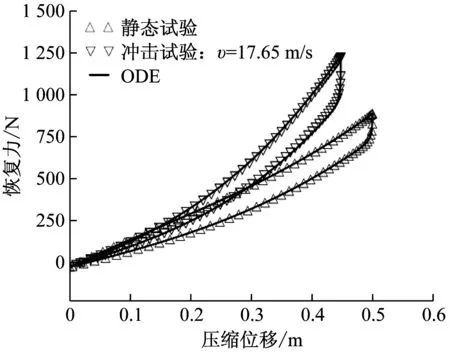
(b) 实测的多股簧响应图4 多股簧的冲击试验Fig.4 Dynamic Impact of stranded wire helical spring
2 火炮自动机动力学模型
为考察三种不同弹簧恢复力模型对自动机运动性能的影响,本文通过分析身管和导气装置之间存在的变质量热力学过程,建立了内弹道耦合导气装置的变质量热力学计算模型,并将计算方程编制成子程序作为边界添加到自动机动力学仿真之中。
2.1 自动机运动原理
本文研究的自动炮为某23 mm导气式航空自动炮,除首发装填需高压气瓶外,自动机的动力源均为导气装置内的气体压力。发射药被点燃后,弹丸在火药燃气压力的作用下挤进膛线并加速向前运动。当弹丸经过导气孔时,部分燃气由导气孔流入导气室,由于内弹道起始阶段膛内气压比气室气压高出很多,导气孔处出现临界流动,此时气室压力逐渐升高并推动传动框加速向后运动;传动框向后运动的同时,带动拨弹板操纵器及其相关机构、加速臂及其相关机构并最终完成开闩、抽壳、拨弹等动作。随着膛内压力下降和传动框运动导致气室容积增大,气室压力达到峰值后开始下降。当传动框上的活塞越过导气室排气孔时,导气室不再提供动力、传动框进入惯性后坐阶段,传动框在复进簧和拨弹板簧的共同作用下逐渐减速,并以一定的速度撞击缓冲器。撞击后传动框和缓冲器一起后坐一定距离,然后在弹簧恢复力和缓冲器推力的作用下加速复进。复进时推弹臂在加速臂和加速座的作用下,加速推弹入膛,当复进到一定位置时,传动框提起炮闩,于此同时自动扣机扣住炮闩上的撞击筒。最后传动框以一定的余速撞击反跳锁,当剩余的能量被消耗后,传动框被反跳锁锁死并停留在最前位置,至此一个射击循环完成。
2.2 自动机有限元模型建模
进行火炮自动机有限元建模时必须对模型进行简化。对于那些刚度大、变形小且对自动机运动影响较小的部件可以当做刚体或者直接将其从计算模型中删去。炮箱作为一个比较复杂的部件,其内部有许多碰撞接触表面,在建模时需要精确处理;由于本文主要关注自动机运动情况,因此只建立药筒模型,并将膛底压力施加在药筒内部;推弹臂和加速臂之间、加速臂和传动框之间采用旋转铰单元建立铰接运动关系,并在这些单元上施加小质量和转动惯量以平衡计算;为了减少计算成本,将炮箱和加速座设定为刚体并将其固定在计算区域中;为了方便弹簧恢复力的施加,分别建立拨弹板簧和复进簧的施力耦合面,并将这些面耦合到弹簧力的施力点上。最终的计算模型共含有13个部件、409 108个实体单元,如下图所示(隐藏炮箱和身管)。
2.3 导气室内火药气体压力计算和载荷施加
由于导气室内的气体压力变化规律与自动机传动框的往复运动有关,因此在计算导气室压力时需将传动框的运动和导气装置气流参数的变化规律耦合起来计算。
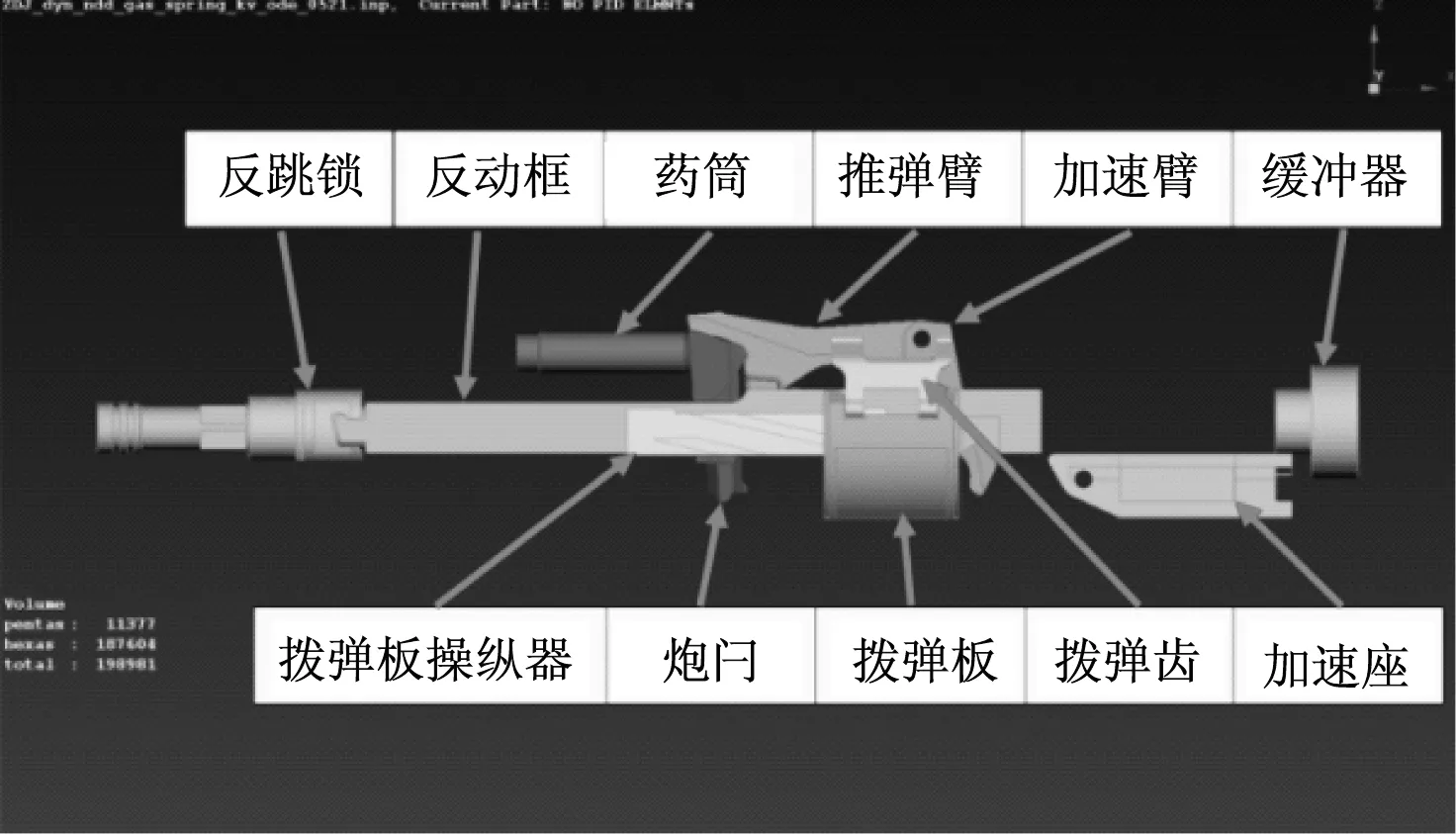
图5 简化的自动机计算模型Fig.5 Simplified computation model of automatic mechanism
以下为当前变质量热力学计算模型的基本假设:
(1) 内弹道采用经典内弹道模型求解,并将后效期膛内气流当作准定常流处理;
(2) 不考虑导气装置内气流参数的分布,将气室内气体压力、密度、温度取平均参数;
(3) 气室与活塞之间的间隙漏气作临界流动处理;
(4) 忽略气体在管道以及间隙中的横向流动效应;
(5) 流动中的气体为完全气体,不计质量力。
导气式自动武器变质量热力学计算模型包括内弹道模型、导气装置模型和导气孔流量(耦合)方程。详细的内弹道方程和导气孔流量方程可以参考相关文献。由于耦合模型中的传动框速度vh、位移xh可以通过ABAQUS的传感器接口向外输出,因此导气室气体参数方程不需要求解传动框的运动参数,于是简化后的导气装置动力学模型如下:
(4)
式中:ρq、pq、Tq分别为导气室内的气体密度、压力和温度;qmb、qmq、Vq0、Sh分别为流入导气室气体流量、导气室间隙的泄漏量、导气室初始容积、活塞的横截面积;γ、Q、R、ei、eq分别为绝热指数、导气室气体对外散热量、火药气体常数、导气室流入和流出单位质量气体所具有的能量。
计算时将内弹道程序输出的膛底压力施加在弹壳内部表面上,结合导气孔处的膛内火药气体压力和密度,将计算得到的导气室压力施加在活塞头端面上。至于复进簧和拨弹板簧的弹簧力,则需要在VUAMP子程序内部调用传动框的位移和速度信息、计算微分方程并将弹簧力施加在相应的耦合节点上;除了9.8 N/m2的重力场之外,以上所施加载荷均使用ABAQUS的VUAMP子程序进行施加,效果如图6(b)所示;模型中的其他载荷(如推弹臂推弹阻力、拨弹齿的弹链阻力)均采用常值的方式简化处理。在有限元模型中设定计算时间为0.05 s,计算终止条件为传动框撞击反跳锁后反弹速度为小于10-7m/s。

(a) 传动框和多股簧的相对位置
3 模型验证及计算结果分析
3.1 模型验证
由于广义BW模型输出的恢复力比较符合实际,因此本文首先使用广义BW模型来验证当前自动机计算模型的准确性。由ABAQUS子程序输出的内弹道压力、导气室压力和弹丸出膛速度分别如图7和图8所示,最大膛内压力、最大导气室压力、弹丸出膛速度分别均为326.0 MPa、40.27 MPa、695.2 m/s,和文献[16]给出的结果分别相差了-0.5%、+2.7%、-1.4%,这说明本文所建立的内弹道/导气装置耦合计算模型是准确的。
当弹丸越过导气孔时(1.179 ms)时,膛内气压很大,导气孔处出现正向临界流动、导气室开始充气;2.2ms时弹丸飞离炮口、内弹道时期结束,膛内气体开始迅速排空,但此时的膛内压力依然高于导气室压力,导气孔处为正向亚临界流动;2.5 ms时导气室压力开始高于导气孔处的膛内压力,导气孔处出现火药燃气的反向流动;随着导气室内的气体不断流入膛内和导气室空间的不断增大,导气室压力逐渐降低;7.87 ms时活塞越过导气室泄气孔,导气室压力降为一个大气压,至此传动框开始进入无动力惯性后坐阶段。
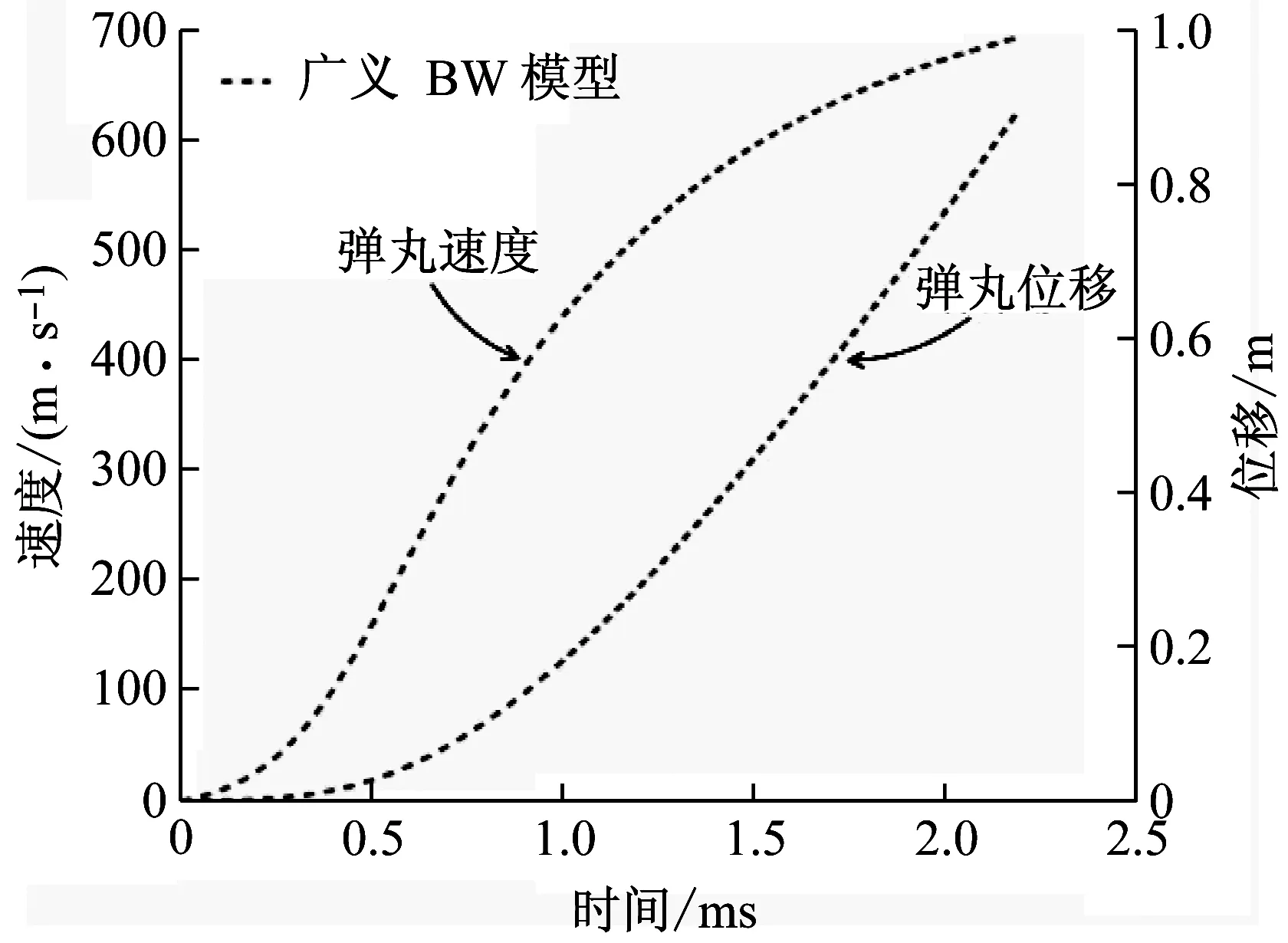
图8 广义BW模型的弹丸速度和位移Fig.8 Displacement and velocity of Generalized BW model
传动框的速度曲线如图9所示,在导气室压力的作用下,传动框的速度不断增大,并在加速臂撞击加速座前达到了最大值16.58 m/s。加速臂撞击加速座时,加速臂相对于传动框旋转的同时,还要后坐并带动推弹臂加速抽壳、抛壳,因此导致传动框的速度有一定的衰减;加速臂和加速座分离后不久,传动框便以10.17 m/s的速度撞击缓冲器,并在弹簧力和缓冲器反力的作用下速度降为0;传动框后坐大约12 mm后开始反弹复进,经过短暂的复进加速后其复进速度达到了最大值8.38 m/s;当其上的加速臂再次和加速座相撞使得推弹臂得以加速推弹入膛后,传动框速度降到6.4 m/s左右。和加速座脱离接触后传动框的速度继续增大,在驱动其他机构和摩擦等消耗的作用下,传动框最终以4 m/s左右的余速撞击反跳锁,并被反跳锁消耗掉剩余的能量而停留在最初的位置上。当前有限元模型所输出的传动框最大后坐速度较文献[17]给出的结果增大5.6%;该炮的理论速射不低于1 200 r/min[16],使用当前模型获得的单次射击循环时间(已包含扣机打火、弹丸启动等时间)为48.243 1 ms,理论速射为1 243.7 r/min。综上所述,可以认为当前所建立的导气式自动机动力学模型是准确的。

图9 广义BW模型的传动框速度Fig.9 Drive box speed of of Generalized BW model
3.2 不同多股簧响应模型对自动机运动性能的影响
三种弹簧响应模型所输出的拨弹板簧恢复力曲线如图10所示。通过对比可以看出,双折线模型的滞回曲线包络面积最大,其线性的加载和卸载关系所产生的恢复力均小于BW模型和广义BW模型,出现这种情况的原因在于静态模型的加载速度太小,使得多股簧簧丝有足够的时间拧紧和放松,从而导致多股簧耗能区间过大、弹簧恢复力较低,因此不足以体现多股簧的非线性渐硬特性;传动框后坐到0.08 m之前,BW模型的恢复力和双折线模型的恢复力基本相等,而在此之后多股簧表现出了非线性刚度,响应曲线开始上翘;计及冲击端速度的广义BW模型由于考虑了冲击时簧圈的惯性效应,弹簧的恢复力分别是BW模型和双折线模型的1.336倍、1.42倍(后坐位移0.16 m时),同时弹簧的滞回耗能也较BW模型有所增加。
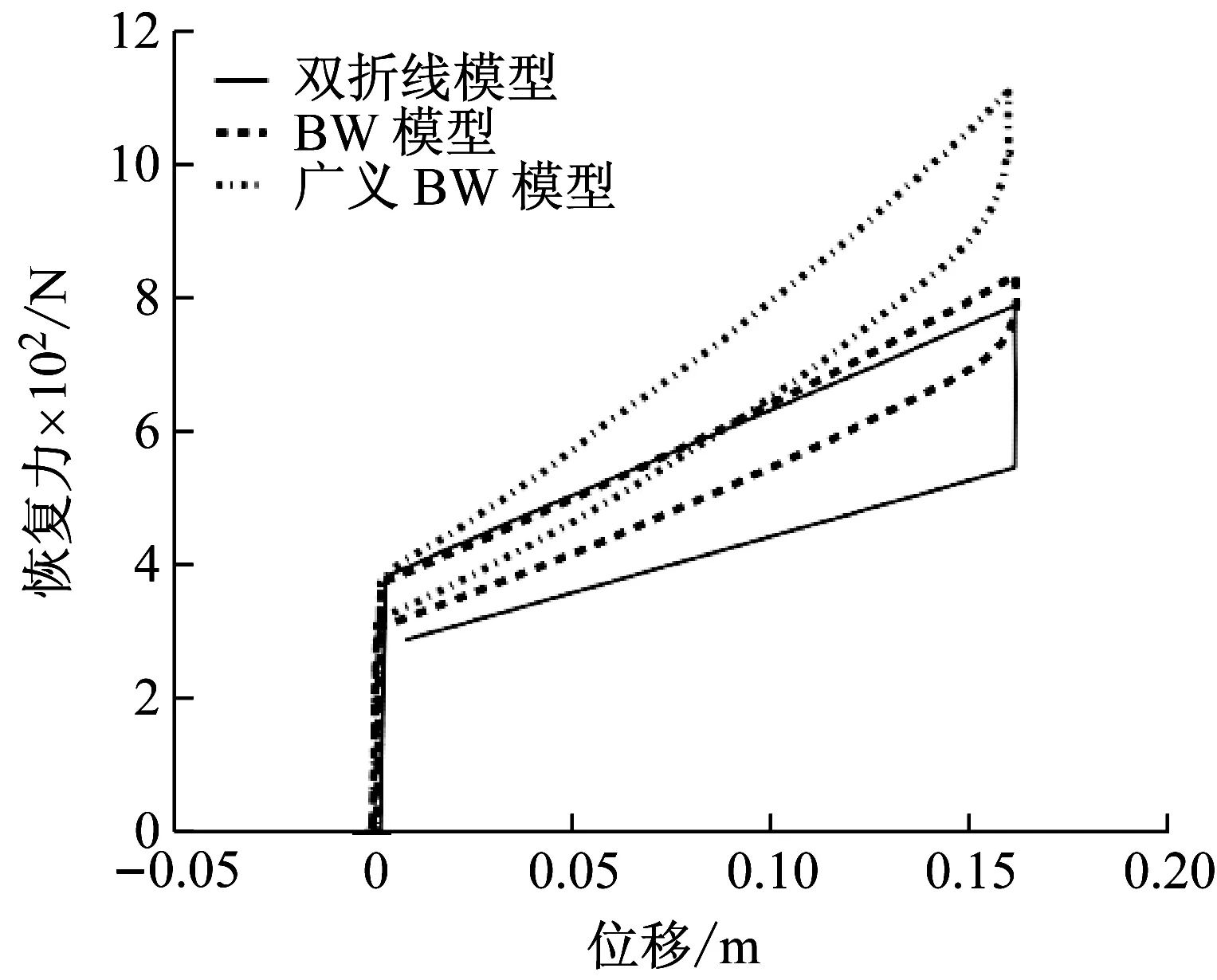
图10 拨弹板簧恢复力的对比Fig.10 Comparison curves of feeding slide spring force
三个模型的传动框速度和位移曲线如图11(a)、(b)所示。从图中可以看出,由于广义BW模型计算出来的弹簧恢复力大大超过了其他两个模型,因此在复进后期传动框复进的动力比较充足、复进速度较大,能够及时地使传动框复进到位,比如0.04 s时,广义BW模型中传动框的速度是BW模型的1.144倍;而双折线模型由于迟滞耗能过大、输出的恢复力过小,导致传动框复进速度过低,在距离前位17 mm处,传动框开始缓慢“爬行”。由于在规定计算时间内不能使传动框复进到位,因而双折线模型无法完成一个射击循环。
三种响应模型的传动框最大后坐速度、位移、单次射击循环耗时和理论射速(理论射速中包含了扣机平均打火时间)如表1所示。由于输出的恢复力高于其他两个模型,广义BW模型的传动框最大后坐速度和位移均小于其他两个模型,但由于复进动力较为充足,所以理论射速高于BW模型。文献[16]认为该武器的理论射速处于1 200~1 350 r/min之间,因此BW模型和广义BW模型的计算结果都比双折线模型更切合实际。

(a) 传动框的速度

(b) 传动框的位移图11 三种响应模型的传动框速度和位移
Fig.11 Drive box speed and displacement curves of three spring response models
表1传动框运动特性和火炮理论射速比较
Tab.1Comparisonofmotioncharacteristicsandtheoreticalshootingrateofdrivebox
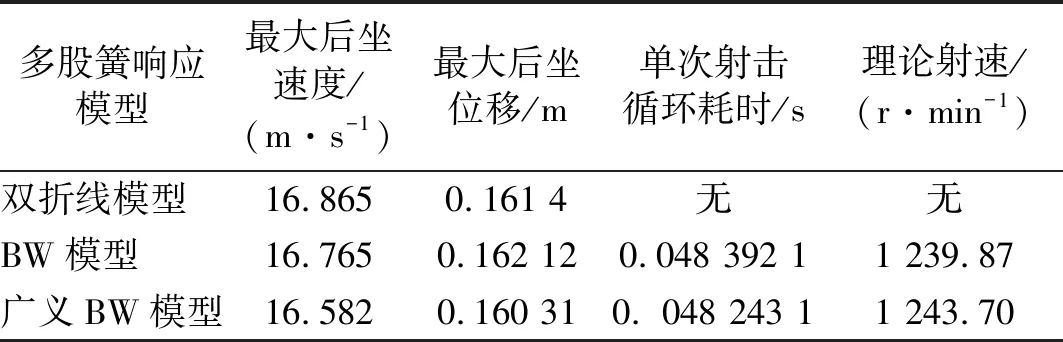
多股簧响应模型最大后坐速度/(m·s-1)最大后坐位移/m单次射击循环耗时/s理论射速/(r·min-1)双折线模型16.8650.161 4无无BW模型16.7650.162 120.048 392 11 239.87广义BW模型16.5820.160 310. 048 243 11 243.70
4 结 论
(1) 本文建立了考虑身管和导气装置耦合过程的火炮自动机有限元模型并将三种多股簧响应模型代入计算。通过分析计算结果并对比相关文献数据,证明当前所建立的内弹道耦合导气室计算模型、自动机仿真模型是准确的。
(2) 基于静态试验的双折线模型由于滞回耗能过大、弹簧恢复力较小,导致传动框复进时动力不足、速度较低,不能有效地使传动框复进到预定位置,这说明装备设计前期所使用的双折线模型并不适用于后期的自动机动力学计算。
(3) 广义BW模型的滞回耗能虽然大于BW模型,但相同后坐位移情况下广义BW模型的恢复力是BW模型的1.336倍,复进速度是BW模型的1.144倍,此时传动框复进动力充足,因此广义BW模型的理论射速高于BW模型。
